第五章 运输问题(运筹学讲义)
运 筹 学 课 件

12/3 4
z
1 2
x4
x5 42
x3
2 3
x4
1 3
x5
4
新典式
主元化 为1,主 元所在
x2
1 2
x4
6
列的其 余元素
x1
2 3
x4
1 3
x5
4
化为0
观察最后一个典式,所有检验数均为非负, 故其对应的基本可行解为最优解,即
X * 4,6,6,0,0T z* 42
去掉引入变量,得原问题的最优解为:
运筹学课件
目录
运筹学概论 第一章 线性规划基础 第二章 单纯形法 第三章 LP对偶理论 第四章 灵敏度分析 第五章 运输问题 第六章 整数规划 第七章 动态规划 第八章 网络分析
第二章 单纯形法
(SM-Simplex Method)
1947年,美国运筹学家Dantzig提出,原理是 代数迭代。
单纯形法中的单纯形的这个术语,与该方法毫 无关系,它源于求解方法的早期阶段所研究的一 个特殊问题,并延用下来。
CB B1b B1b
z
CB B1N CN X N X B B1NX N
CB B1b B1b
上述方程组的矩阵形式为
10
0 I
CB
B1N B1N
CN
z XB XN
CB B1b B1b
上式的系数增广阵称为对应于基B的单纯形表:
T(B)
CB B1b B1b
0 I
CB
B1N B1N
CN
形式的LP问题,必须解决三个问题: ⑴初始基本可行解的确定; ⑵解的最优性检验; ⑶基本可行解的转移规则。 这里先放一下⑴,研究⑵和⑶,为此,
运筹学运输问题

当出现检验数<0,证明原初始方案或改 进方案还不是最优→如何进行基变量的 调入调出?
给检验数<0的非基变量赋值,越大 越好。但要考虑产销平衡问题。
11
8、运输问题的校验方法2 —位势法
利用行位势和列位势两类数据,将检验数与 单位运价联系起来
12
检 验 数 方 程
13
λ
= c – u – v ij ij i j
A、位势法求检验数的步骤
第一步:根据最小元素法或Vogel法确定的初始运量表做 一表格,将基变量(或运量)数据替换成与之对应的单位 运价;(或对单位运价表进行修改,只保留与基变量对应的运价信
息)
第二步:在右侧增加一列,下侧增加一行,用于填写位势 数据。右侧表示行位势ui(i=1,2...m),下侧表示列位 势vj(j=1,2...n); 第三步:对于基变量对应的单位运价处,ui+vj=cij。随便 确定任一个位势,即可求解全部行和列位势; 第四步:在非基变量对应的空格处,计算检验数λij=cij(ui+vj)。并将检验数填入检验数表中; 第五步:判断检验数λij是否大于0,如是,则表示较优。 如不是,则需要调整基变量。 第六步:基变量的调整采用闭回路法进行。
收点 发点 9
B1
4
B2
1
B3
11
B4 -1
10 5
发量
偶 点 0 减 , 2 奇 点 加 5
A1
14 ③奇点 9 18 1 A2 x x 1 9 11 6 8 0 A3 1 3 x 14 ②偶点 12 2
11 21 22 31
x 3 2
x 6 7
5
13
偶点④
9
韩伯棠管理运筹学第三版-第七章-运输问题分析ppt课件.ppt

B1 B2 B3 产量
A1 6 4 6
200
A2 6 5 5 销量 250 200 200
300 500
650 23
B1 B2 B3
产量
A1
6
4
6
200
A2
6
5
5
销量 250 200 200
300 500
650
解:增
B1 B2 B3
加一个 A1 6 4 6
虚设的 A2 6 5 5
产地运 A3 0 0 0 输费用 销量 250 200 200
6
4 6 200
A2
6
5 5 300
销量 150 150 200
B1
B2
B3 产量
A1
x11
x12
x13 200
A2
x21
x22
x23 300
销量 150 150 200
Min f = 6x11+ 4x12+ 6x13+ 6x21+ 5x22+ 5x23
A1 A2 销量
B1 6 6 150
B2 4 5 150
§2
运输问题的计算机求解
运行管理运筹学计算机软件:
点击运输问题模块
14
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
§2
运输问题的计算机求解
点击新建
选择Min
输入3
输入4
点击确定
15
在日常生活中,随处都可以看到浪费 粮食的 现象。 也许你 并未意 识到自 己在浪 费,也 许你认 为浪费 这一点 点算不 了什么
物流系统分析第五章ppt课件

毛利 (元) 30000 39000 45000
运输成本核算 (元) 3750 11700 23287.5
净利润 (元) 26250 27300 21712.5
思考:本例中应进一步分析的问题
16
三、运输工具配置
运输工具的类型
运输工具的选择应以货物的需要为前提 物流企业初建期,应根据企业预期的细分市场的需
D对 流现象的图示D
q
A q
A
• qE
C
• q
×
B
B
C
当运输线路不形成 圈时,只要调运方案的 流向图不出现对流,那 么这个调运方案一定是 最好的。
19
四、运输线路规划
迂回现象的图示
q
C 3km
B•
C
3km
2km
• D 3k m
2km
4k
m
A×
D• 3km
•B 4km
A
只要使内圈或外圈流向长度小于等于圈长的一半,
运输时间的可靠性
准时到达送货的比例、准时发货的比例、两次事故的间隔 时间
时间
在途时间、车辆装卸时间、滞留时间、运行迟滞时 间等
8
四、运输系统规划的内容
运输业务模式的选择
自营运输与外包运输的选择
运输方式的选择
公路、铁路、水路、航空、管道
运输批量和运输时间的确定 运输路线的规划与选择
送 应当避免停留点工作时间太短的约束
28
四、运输线路规划
制定车辆运行路线 扫描法 最近点连接法 最优插入法
多品种货物调运问题
各种货物之间不能相互替代 根据不同货物的供需关系分别建立运输模型,或者是令不同品 种货物的供需点之间不能形成供需关系(令相应的单位运价为 M,M为一充分大的正数),再建立运输模型,即可运用表上 作业法求解。
运筹学运输问题-图文

销地 B1
B2
...
Bn
产量
产地
A1
X11 X12
...
X1n
a1
A2
X21 X22
...
X2n
a2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Am
Xm1 Xm2
...
Xmn
am
销量
b1
b2
...
bn
则运输问题的数学模型如下:
产销平衡表
销地 B1
B2
...
Bn
产量
产地
A1
a1
A2
a2
.
.
.
.
.
.
Am
am
销量
b1
b2
...
bn
单位运价表
销地
B1
B2
...
Bn
产地
A1
c11
c12
...
c1n
A2
c21
c22
...
c2n
.
.
.
.
.
.
.
.
.
.
.
.
Am
cm1
cm2
...
cmn
❖ 若总产量等于总销量(产销平衡),试确定总运费最省 的调运方案。
Table14 检验数表
销地
B1
B2
B3
B4
产地
A1
管理运筹学讲义运输问题

管理运筹学讲义运输问题引言在现代社会,运输问题是管理运筹学中的一个重要问题。
无论是物流行业还是供应链管理,运输问题都是必不可少的一环。
运输问题的解决可以帮助企业有效地规划和管理物流流程,降低运输成本,提高运输效率。
本文将介绍管理运筹学中的运输问题,包括问题的定义、数学模型、常用的解决方法以及在实际应用中的案例分析。
运输问题的定义在管理运筹学中,运输问题是指在给定的供应点和需求点之间,如何分配物品的问题。
通常,问题的目标是找到一种分配方案,使得总运输成本最小。
运输问题可以抽象成一个图模型,其中供应点和需求点之间的路径表示运输线路,路径上的边表示运输的数量和成本。
每个供应点和需求点都有一个需求量或供应量。
问题的目标是找到一种分配方案,使得满足所有需求量的同时最小化总运输成本。
数学模型运输问题可以用线性规划来建模。
假设有m个供应点和n个需求点,每个供应点的供应量为si,每个需求点的需求量为dj。
定义xij为从供应点i到需求点j 的运输量,则运输问题的数学模型可以形式化表示为如下线性规划问题:minimize ∑(i=1 to m)∑(j=1 to n) cij * xijsubject to∑(j=1 to n) xij = si, for all i = 1,2,...,m∑(i=1 to m) xij = dj, for all j = 1,2,...,nxij >= 0, for all i = 1,2,...,m and j = 1,2,...,n其中cij表示从供应点i到需求点j的运输成本。
解决方法针对运输问题,常用的解决方法有以下几种:1. 单纯形法单纯形法是一种用于解决线性规划问题的常用方法。
对于运输问题,可以通过将其转化为标准的线性规划问题,然后使用单纯形法来求解最优解。
2. 匈牙利算法匈牙利算法是一种经典的图论算法,可以用于解决运输问题。
算法的核心思想是通过不断寻找增广路径来寻找最大匹配。
3. 运筹学运输问题
X ij a i ( i 1, 2 ,..., m ) j1 m X ij b j ( j 1, 2 ,..., n ) i 1 X 0 ( i 1 , 2 ,..., m , j 1 , 2 ,..., n ) ij
13
销地 运价 产地
B1
B2
B3
B4
B5
产量(万吨)
A1 A2
7 5
10 9
30 40
8 7
0
6 +0 20 4 -0 12-0
0
20
40 40
6
+0
A3
销量(万吨)
3
30
B1
6
40
B2 10 9
40
5
60
B3 8 7 5 60ຫໍສະໝຸດ 60820
B4 6
11
20
B5
20 4
90
产量(万吨)
20 40 0
A1 A2 A3 销量(万吨)
①用最小元素法确定初始方案(即初始基可行解)
基本思想:最小费用法是尽可能选取单位费最小的变量作为基 变量。然后尽可能多地满足它的需要,再划去满足的行(或列,若行 列同时满足,也只划去一行或一列),接着对未划去的行和列调整供 4 应量和需要量,继续上述步骤,直到得到初始可行基解。
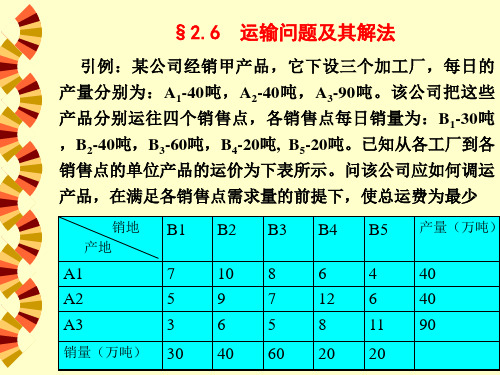
例18(P37)设某产品从产地A1,A2,A3运往销地B1, B2,B3,B4,B5,运量和单位运价如下表所示,问如何 调运才能使总的运费最少?
i 1 j 1 3 5
X 11 X 21 X 31 X 11 s . t . X 12 X 13 X 14 X 15 X ij
运筹学讲义影子价格-灵敏度分析-运输问题

2)
0.000000
48.000000
3)
0.000000
2.000000
4) 40.000000
0.000000
35元可买到1桶牛奶,要买吗? 35 <48, 应该买!
聘用临时工人付出的工资最多每小时几元? 2元!
21
结果解释
DO RANGE(SENSITIVITY) ANALYSIS?
Yes
RANGES IN WHICH THE BASIS IS UNCHANGED: OBJ COEFFICIENT RANGES
20桶牛奶生产A1, 30桶生产A2,利润3360元。
18
模型求解
OBJECTIVE FUNCTION VALUE
1)
3360.000
VARIABLE VALUE REDUCED COST
X1 20.000000
0.000000
X2 30.000000
0.000000
ROW SLACK OR SURPLUS DUAL PRICES
16
1桶
12小时 3公斤A1
牛奶 或 8小时 4公斤A2
获利24元/公斤 获利16元/公斤
每天 50桶牛奶 时间480小时 至多加工100公斤A1
决策变量 目标函数
约束条件
x1桶牛奶生产A1 x2桶牛奶生产A2
获利 24×3x1
获利 16×4 x2
每天获利 Max z 72 x1 64 x2
原料供应
12
影子价格的经济意义:在资源得到最优配置,使总效益最大时,该资源投 入量每增加一个单位所带来总收益的增加量。
影子价格是一种静态的资源最优配置价格,不能表现资源在不同时期动态 配置时的最优价格,只反映某种资源的稀缺程度和资源与总体积极效益之间 的关系,不能代替资源本身的价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当我们取定xij的值之后,会出现Ai的产量与Bj的需求量都改 为零的情况,这时应同时划去Ai行与Bj列。既在划去xij对应 一行(列),填上一个数时,也应划去xij对应列(行),在 任意被划去除xij 以外任一格内填上 0,这时出现退化解。
盐湖城
萨克拉门 托仓库
WAREHOUSE 4 Albuquerque
澳尔巴古 奥尔巴古
P&T公司问题中的仓库和加工厂位置图
相关数据 Shipping Data
罐头厂 Output产量 75 车 125车 100车
仓库
萨克拉门托 盐湖城 赖皮特
分配量Allocation 80 车 65车 70车
贝林翰 尤基尼
80
31
416 x22 682 x
32
65
690 x23 388 x33
70
791 x24
685 x34
85
125
100
线性规划模型
设Let xij = 从罐头厂i 运往仓库j卡车数 the number of truckloads to ship from cannery i to warehouse j (i = 1, 2, 3分别表示贝林翰罐头厂,尤基尼罐头厂,艾 尔贝.李罐头厂; j = 1, 2, 3, 4分别表示萨克拉门托仓库,盐湖城仓库,赖皮特 仓库和澳尔巴古仓库) 则线性规划模型为
1.最小元素法
最小元素法是就近供应,即对单位运价最小的变量分配运输量。 假定运价表中cij 最小, 则分配运量xij ,使xij取尽可能大的值 xij=Min{ai, bj} 。即如果ai>bj ,则取xij= bj,删除运价表中第j列, 修改剩余产量为ai- bj 。 否则若bj >ai ,则取xij = ai, 删除运价表中第i行,修改剩余需求 量bj - ai
差值法基于这种考虑,先计算所有行和列次小运费和最小运 费的差值(称为行差值和列差值),找出最大的差值,然 后根据其所在的行或列的最小运费来确定运量的分配。
差值法例 P58
增加行差值和列差值
B1
A1 6 9
B2
B3 12 7
B4
ai
60
行差值 1
1 A2 5 A3
3
6
1
(42)
1 3 4
42 0
0
48 50 30 25 45
3、成本假设:从任何一个出发地到任何一个目的地的货物配送成本和所 配送的数量成线性比例关系,因此这个成本就等于配送的单位成本乘 以所配送的数量
4、整数解性质:当供应量和需求量都是整数,必存在决策变量均为整数 的最优解
运输问题解中非零变量的个数不超过m+n-1个,因为m+n个约束中只有 m+n-1个是独立的。基变量在迭代过程中保持为m+n-1个。 用单纯形来求解运输问题,需要加m+n个人工变量,产生一个变量数 为mn +m+n的线性规划,求解比较复杂,需要寻求更简便的解法。
45
0
bj
由此可以得到初始可行解为:
x21=42; x32=30; x33=18; x11=8; x14=45; x13=7
初始方案的运输费用为: f1=6×8+12×7+7×45+1×42+1×30+3×18=573
2 差值法Vogel’s 法
计算运价表各行各列中最小两个运价之差值
最小元素法可能导致其他供销点以更高的运费分配运量。次 小运费和最小运费的差额越大,说明在该处如果不能以最 小运费运送,按次小运费运送的费用将很大,因此次小运 费和最小运费的差额为该供应地和需求地的罚数。若罚数 的值不大,当不能以最小运费安排运输量时造成的运费损 失不大;反之,如果罚数的值很大,不按最小运费安排运 输量时造成的运费损失很大。
物流中的一个普遍问题是如何以尽可能小的成本把
货物从一系列起始地(sources)(如工厂、仓库
)运输到一系列终点地(destinations)(如仓库 、顾客)
想想看!
如何分析这类问题
§1 运输问题模型实例 The P&T Company
分配网络 P189
例1 P&T公司是一家主要生产豌豆罐头的公司。它收购豌豆 并在食品罐头厂把它们加工成为罐头,然后再把这些罐头 食品分销到各地卖出去。豌豆罐头在三个食品罐头厂(靠 近华盛顿的贝林翰;俄勒冈州的尤基尼;明尼苏达州的艾 尔贝· 李)加工,然后用卡车把它们运送到美国西部的四 个分销仓库(加利福尼亚州的萨克拉门托;犹他州盐湖城; 南达科他州赖皮特城;新墨西哥州澳尔巴古)
B1
A1 6 9
B2
B3 12 7
B4
ai
(45)
60
行差值 1
(8)
1 3
(7)
6 1
A2 5 A3
(42)
1 3 4
0
(23)
8 30 0
(25)
45
23
0
3
bj
列差值
1
8
3
7
b2 =30 > a3=23
差值法例 P58
B1 A1 6 9 B2 B3 12 7 B4
ai
60
(8)
1 3
(7)
6 1
ai
(42)
5 1 3 4
b1=50> a2 =42
A3
0
48
bj
50
8
30
25
45
最小元素法(续)
B1 A1 6 9
B2
B3 12 7
B4
ai
60
1
3
6
1
A2
5 A3
(42)
1 3 4
0
(30)
8 30 25 45
48
18
bj
0
a3 =48 > b2=30
最小元素法(续)
B1 A1 6 9
B2
(45)
A2 5 A3
(42)
1 3 4
42
(23)
50 30
(25)
25 45
48
bj
由此可以得到初始可行解为:
x11=8; x12=7; x14=45; x21=42; x32=23; x33=25;
初始方案的运输费用为: f1=6×8+9×7+7×45+1×42+1×23+3×25=566
上述计算过程可用流程图描述如下
取未划去的单元格xij ,令 xij = min { ai , bj }
ai’ = ai - xij bj’ = bj - xij
否
ai’ = 0? 否 bj’ = 0
划去第i行
是
否所 均有 被行 划列 去是
是 找到初始基 本可行解
划去第j列
求运输问题的初始基本可行解过程
u1 1 u2 um v1 1 v2 vn 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 m行 n行
B3 12 7
B4
ai
60
1
3
6
1
0
A2
5 A3
(42)
1 3 4
(30)
8 0
(18)
25 45
18
0
bj
b3=25> a3 =18
7
最小元素法(续)
B1 A1 6 9 B2 B3 12 7 B4
ai
60
(8)
1 3 6
(7)
1
(45)
A2 5 A3
(42)
1 3 4
0
(30)
8 0 7
(18)
Chapter 5 运输问题与指派问题
Transportation and Assignment Problem
§1运 输 模 型The Transportation model §2运输问题表上作业法 §3运输问题网络模型 Transportation Network §4 应用实例
运输问题 The Transportation Problem
P&T Company Distribution Problem
贝林翰罐 头工厂 尤基尼 工厂
CANNERY 1 Bellingham
赖皮特
WAREHOUSE 3 Rapid City
艾尔贝.李工厂
CANNERY 3 Albert Lea
CANNERY 2 Eugene
WAREHOUSE 2 Salt Lake City WAREHOUSE 1 Sacramento
min f cij xij
i 1 j 1
m
n
s.t.
m
x
j 1
n
ij
ai i 1,2,, m
x
i 1
ij
b j j 1,2, , n
xij 0 i 1 , 2 ,, m
B1 A1 c11 [x11] B2
j 1 , 2 ,, n
…… ……
Bn c1n [x1n]
Minimize Cost = 464x11 +513x12 + 654x13 +867x14 +352x21 + 416x22 +690x23 + 791x24 + 995x31 + 682x32 + 388x33 + 685x34 subject to 罐头厂 1: x11 + x12 + x13 + x14 = 75 罐头厂 2: x21 + x22 + x23 + x24 = 125 罐头厂 3: x31 + x32 + x33 + x34 = 100 仓库 1: x11 + x21 + x31 = 80 仓库 2: x12 + x22 + x32 = 65 仓库 3: x13 + x23 + x33 = 70 仓库 4: x14 + x24 + x34 = 85 xij ≥ 0 (i = 1, 2, 3; j = 1, 2, 3, 4)
