图像放大算法
图像放大算法范文

图像放大算法范文图像放大算法是指将低分辨率图像放大到高分辨率的过程。
在图像处理中,图像放大是一个具有挑战性的问题,因为放大图像时往往会引入模糊、失真等问题。
然而,通过使用一些高级的算法和技术,可以获得更好的放大效果。
在实际应用中,图像放大主要有两种方式:插值和超分辨率。
插值是一种基本的图像放大技术,它利用邻近像素的信息对低分辨率图像进行放大。
最简单的插值算法是最近邻插值,在放大时将每个像素复制为一个矩阵区域。
这种算法易于实现,但会导致锯齿状的边缘。
另一种常用的插值算法是双线性插值,它使用邻近的四个像素的信息进行插值计算。
这种算法较第一种算法的效果更好,但对于边界和细节较为平滑的图像效果较差。
超分辨率是一种通过利用多个低分辨率输入图像来产生高分辨率图像的技术。
这种技术通常需要在训练期间学习一个映射函数,然后将其应用于输入图像。
近年来,基于深度学习的超分辨率算法取得了显著的成果。
其中最著名的算法是SRCNN(超分辨率卷积神经网络)和ESPCN(极速超分辨率)。
这些算法通过深度卷积神经网络学习输入图像与目标图像之间的映射,达到超分辨率的效果。
除了插值和超分辨率之外,还有一些其他的图像放大算法。
例如,自适应边缘增强(AEE)算法可以通过增强边缘信息来提高图像的质量。
另外,基于频域的算法,如小波变换,也常用于图像放大领域。
这些算法将图像从空域转换到频域,利用频域的特性对图像进行放大处理。
总结起来,图像放大算法是一个涉及到信号处理、图像处理和机器学习等多个领域知识的复杂问题。
插值和超分辨率是两种常用的图像放大方式,它们分别通过邻近像素的信息和多个输入图像的映射来实现图像放大。
此外,还有一些其他的算法,如自适应边缘增强和基于频域的算法,也可用于图像放大领域。
随着科技的发展,越来越多的新算法将会被提出,并不断改进图像放大的效果。
基于阶梯细化的图像放大算法研究解读

基于阶梯细化的图像放大算法研究
数字图像放大是重要的图像处理技术之一,在众多领域都有重要的应用。
数字图像放大就是将原始图像的分辨率提高,基本的方法是图像插值。
图像插值的算法很多,如经典的最近邻域插值、双线性插值等。
图像放大算法面临的两个主要问题是放大的图像会出现细节模糊化和边缘的锯齿失真。
本论文针对图像放大时边缘出现的锯齿失真,分析锯齿出现的原因,提出数字图像中的边缘是由一系列阶梯构成的,是不连续的;并认为边缘的这种不连续性在图像放大过程中也被放大,从而产生锯齿失真。
根据上述分析,本论文提出了基于阶梯细化的图像放大算法。
该算法是一种综合性的算法,即在图像的非边缘区域采用经典的双线性插值算法;同时根据Canny边缘检测的结果,进一步进行阶梯检测,滤除不会产生锯齿失真的竖直和水平边缘,在使用经典算法会产生明显锯齿失真的包含一系列阶梯的边缘区域,运用基于阶梯细化的插值算法。
该插值算法在放大图像的同时,抑制了边缘中的阶梯被放大,从而达到减少锯齿失真的目的。
最后的实验结果对比和分析表明,在阈值设置合适的前提下,该算法可以在一定程度上抑制边缘锯齿失真。
【关键词相关文档搜索】:通信与信息系统; 图像处理; 图像放大; 阶梯细化; 插值; 锯齿效应
【作者相关信息搜索】:兰州大学;通信与信息系统;万毅;侯国强;。
图像放大的两种编程算法的实现
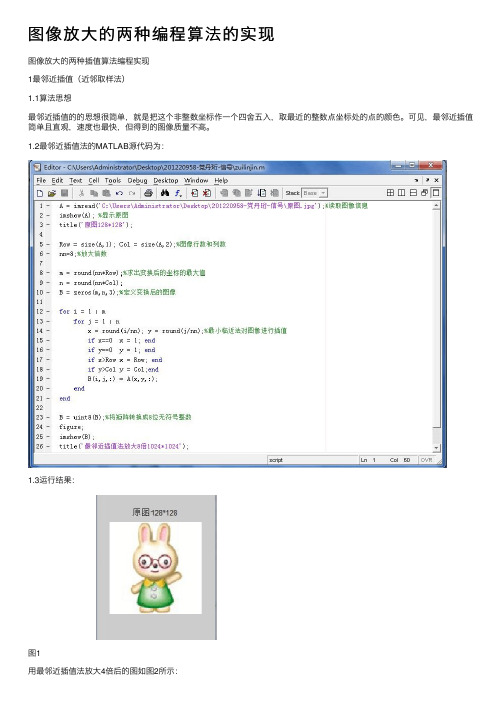
图像放⼤的两种编程算法的实现图像放⼤的两种插值算法编程实现1最邻近插值(近邻取样法)1.1算法思想最邻近插值的的思想很简单,就是把这个⾮整数坐标作⼀个四舍五⼊,取最近的整数点坐标处的点的颜⾊。
可见,最邻近插值简单且直观,速度也最快,但得到的图像质量不⾼。
1.2最邻近插值法的MATLAB源代码为:1.3运⾏结果:图1⽤最邻近插值法放⼤4倍后的图如图2所⽰:图22双线性内插值法2.1算法思想在双线性内插值法中,对于⼀个⽬的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v),其中i、j均为⾮负整数,u、v为[0,1)区间的浮点数,则这个像素得值f(i+u,j+v)可由原图像中坐标为(i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:f(i+u,j+v)=(1-u)(1-v)f(i,j)+(1-u)vf(i,j+1)+u(1-v)f(i+1,j)+uvf(i+1,j+1)其中f(i,j)表⽰源图像(i,j)处的的像素值,以此类推。
这就是双线性内插值法。
双线性内插值法计算量⼤,但缩放后图像质量⾼,不会出现像素值不连续的的情况。
由于双线性插值具有低通滤波器的性质,使⾼频分量受损,所以可能会使图像轮廓在⼀定程度上变得模糊。
在MATLAB中,可⽤其⾃带的函数imresize()来实现双线性内插值算法。
2.2程序代码双线性内插值算法的MATLAB源代码为:2.3运⾏结果程序运⾏后,原图如图3所⽰:图3双线性内插值法放⼤8倍后的图如图4所⽰:图43结论最近邻插值运算简单快速,能够保持插值图像边缘清晰,但边缘轮廓有显著的锯齿现象,图像背景产⽣马赛克,形成伪边缘,视觉效果差,重构误差较⼤与最邻近法相⽐,双线性内插法由于考虑了待采样点周围4个直接邻点对待采样点的影响,因此基本克服了前者灰度不连续的缺点,其计算量有所增⼤。
此⽅法仅考虑4个直接邻点灰度值的影响,⽽未考虑到各邻点间灰度值变化率的影响,因此具有低通滤波器的性质,使放⼤后图像的⾼频分量受到损失,图像的轮廓变得较模。
利用双线性插值法实现图像放大
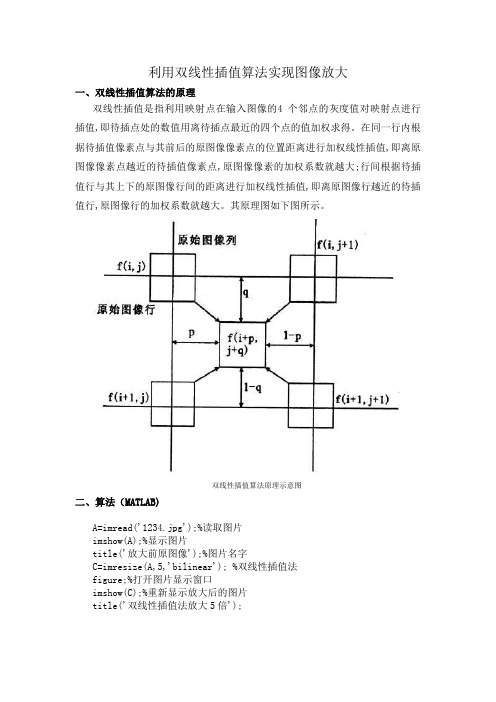
利用双线性插值算法实现图像放大
一、双线性插值算法的原理
双线性插值是指利用映射点在输入图像的4 个邻点的灰度值对映射点进行插值,即待插点处的数值用离待插点最近的四个点的值加权求得。
在同一行内根据待插值像素点与其前后的原图像像素点的位置距离进行加权线性插值,即离原图像像素点越近的待插值像素点,原图像像素的加权系数就越大;行间根据待插值行与其上下的原图像行间的距离进行加权线性插值,即离原图像行越近的待插值行,原图像行的加权系数就越大。
其原理图如下图所示。
双线性插值算法原理示意图
二、算法(MATLAB)
A=imread('1234.jpg');%读取图片
imshow(A);%显示图片
title('放大前原图像');%图片名字
C=imresize(A,5,'bilinear'); %双线性插值法
figure;%打开图片显示窗口
imshow(C);%重新显示放大后的图片
title('双线性插值法放大5倍');
三、程序运行结果截图。
双线性插值图像放大算法优化及硬件实现

2、双线性插值硬件加速器设计
基于FPGA的双线性插值硬件加速器主要由输入模块、计算模块和输出模块三 部分组成。其中,输入模块负责接收来自外部的图像数据;计算模块负责执行双 线性插值算法;输出模块负责将计算结果输出到外部设备。
2、双线性插值硬件加速器设计
在计算模块中,我们采用了基于加权平均法和边缘保护法的双线性插值算法。 具体来说,我们对四个相邻像素点进行加权平均,并根据目标像素点的位置关系 分配不同的权重。同时,我们还会对目标像素点的周围像素点进行判断,如果存 在边缘信息,则会保护这些信息不被丢失。
2、双线性插值硬件加速器设计
在实现过程中,我们采用了Verilog硬件描述语言来编写算法的硬件实现代码。 在代码编写过程中,我们采用了流水线架构和并行计算技术,提高了算法的执行 效率。我们还采用了一些优化技巧,如逻辑优化、时序优化等,提高了硬件加速 器的性能和稳定性。
3、实验结果与分析
3、实验结果与分析
双线性插值图像放大算法优 化及硬件实现
目录
01 一、双线性插值算法 的优化
03 参考内容
02
二、双线性插值算法 的硬件实现
内容摘要
随着图像处理技术的发展,图像放大已成为图像处理中一个重要的环节。在 图像放大过程中,由于分辨率的降低和图像信息的损失,图像的质量往往会受到 严重影响。为了提高图像的质量,可以采用插值算法对图像进行放大。其中,双 线性插值算法是一种常用的方法,它通过对图像中相邻的四个像素点进行线性插 值,得到放大后的像素值。
2、边缘保护法
2、边缘保护法
在双线性插值算法中,当目标像素点位于图像边缘时,其周围的四个相邻像 素点可能会缺失。这时,如果直接进行线性插值,会导致放大后的图像边缘模糊 甚至出现黑边。为了解决这个问题,我们引入了边缘保护法。具体来说,我们在 计算目标像素点的值时,会根据其周围的像素点的位置关系,给它们分配不同的 权重。这样就可以更好地保护图像的边缘信息,提高图像的质量。
图像放大缩小的原理和应用

图像放大缩小的原理和应用1. 原理图像放大缩小是数字图像处理中的一种基础操作,其原理是通过改变图像像素的尺寸来实现。
在图像放大时,通常采用插值算法来填充空白像素;而在图像缩小时,通常采用像素平均或取样的方式来减少像素。
1.1 图像放大原理图像放大的主要原理是通过插值算法来增加图像的像素数量,从而增大图像的尺寸。
插值算法可以根据原图像的像素值,在新的像素位置上生成合适的像素值。
常用的插值算法包括最近邻插值、双线性插值和双三次插值等。
最近邻插值是一种简单的插值算法,它通过找到离新像素位置最近的像素值来进行插值。
这种算法简单快速,但会导致图像边缘的锯齿效应。
双线性插值是一种更精确的插值算法,它考虑了新像素位置附近的像素值,并进行线性插值计算。
这种算法可以有效地减少锯齿效应,但对于像素边缘仍可能存在模糊问题。
双三次插值是一种更高级的插值算法,它在双线性插值的基础上添加了更多的像素信息,通过曲线拟合来生成更精确的像素值。
这种算法可以进一步减少锯齿效应和模糊问题,但计算复杂度也相应增加。
1.2 图像缩小原理图像缩小的主要原理是通过减少图像的像素数量来缩小图像的尺寸。
常用的缩小算法包括像素平均和取样算法。
像素平均算法是一种简单的缩小算法,它将原图像中的多个像素的 RGB 值取平均,生成新的像素值。
这种算法简单快速,但会导致图像细节丢失。
取样算法是一种更精确的缩小算法,它通过从原图像中选择几个有代表性的像素进行采样,并生成新的像素值。
这种算法可以保留更多的图像细节,但计算复杂度也相应增加。
2. 应用图像放大缩小在许多领域都有广泛的应用,下面列举了几个常见的应用场景:•数字摄影:在数字摄影中,图像放大可以用于增加图像的分辨率,从而提高图像的清晰度和细节呈现。
•医学影像:在医学影像领域,图像放大可以用于放大细胞、组织或病变区域,帮助医生进行更精确的诊断。
•图像处理:在图像处理领域,图像缩小可以用于生成缩略图,帮助用户快速浏览和索引大量图像;图像放大可以用于图像重建和增强,帮助改善图像质量。
Adobe Photoshop中的照片放大和插值方法

Adobe Photoshop中的照片放大和插值方法在摄影中,我们经常会遇到需要对照片进行放大的情况。
这可能是因为我们想要将一张小的照片变大以显示更多细节,或是因为我们需要打印一张大尺寸的照片。
不过,照片放大并不是一件容易的事情。
当我们简单地将照片放大时,通常会导致失真和像素化的问题。
为了解决这个问题,Adobe Photoshop提供了一些照片放大和插值方法。
在Adobe Photoshop中,有两种主要的方法用于照片放大:规格化和智能插值。
首先,让我们来看看规格化这种方法。
规格化是一种相对简单的放大方法,它通过在每个像素之间复制和重复像素来增加图像的大小。
这种方法在某些情况下可能效果不错,特别是当我们只需要轻微放大照片时。
然而,当我们需要大幅度放大照片时,规格化方法可能会导致像素化和失真。
这是因为规格化不能增加图像的细节,而只是简单地放大现有的像素。
因此,当我们需要放大照片时,规格化可能并不是最好的选择。
而另一种方法——智能插值——则提供了更好的照片放大效果。
智能插值是一种基于算法的方法,它通过分析图像的像素分布和模式来重新构建图像,并增加细节以适应放大的尺寸。
相较于规格化,智能插值的结果要更自然和清晰。
它可以通过使用不同的插值算法来实现,例如双线性插值、双立方插值和自适应插值。
双线性插值是一种相对简单的插值算法,它假设图像中的像素间距是均匀的。
双线性插值通过计算每个新像素的值,以及其周围像素的加权平均值来进行图像放大。
这种方法在某些情况下可能效果不错,但在放大大图像时可能会导致某些细节的模糊。
与双线性插值相比,双立方插值是一种更高级的插值算法。
它通过计算每个新像素的值,以及其周围像素的加权平均值来进行图像放大。
与双线性插值相比,双立方插值考虑了更多周围像素的信息,从而产生更精确和清晰的结果。
当我们需要放大照片时,双立方插值通常是一个更好的选择。
同时,Adobe Photoshop还提供了一种自适应插值方法。
基于模糊推理的图像放大算法

U i r t o ot a dT l o m nct n ,N nig 10 3 C i ) n esy f s n e cm u i i s aj 00 , hn v i P s e ao n2 a
Absr c :I a e z o t c iuep a s a mp ra trl n ma y i a e a pi ain s se . Sn e f zy t a t m g o m e hnq l y n i o tn oe i n m g p l to y t ms c ic u z fau e i n ft e m an i g h r ce sis a n v li g o m t o a e n f z y r a o i g i e tr so e o h i ma e c a a t r t , o e ma e z o meh d b s d o u z e s n n s i c
I a e Zo m e h d Ba e o Fu z a o ng m g o M t o s d n z y Re s ni
G N Z n -a g Q i a A ogl n , I — i LH
( i guP o ic e a f n g rc s n J n s rv e K yL bo h a eP oe s g& I a eC m nct n N ni a n i m g o mu ia o . aj g i n
jcn aepxl aec niee sakn f pc i fz neec ue a dtefzyrlsr i aet m g i s r o s rda ido eic u z if n erl n h z e e n i e d s f y r s u u ma
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、图像放大算法
图像放大有许多算法,其关键在于对未知像素使用何种插值方式。
以下我们将具体分析几种常见的算法,然后从放大后的图像是否存在色彩失真,图像的细节是否得到较好的保存,放大过程所需时间是否分配合理等多方面来比较它们的优劣。
当把一个小图像放大的时候,比如放大400%,我们可以首先依据原来的相邻4个像素点的色彩值,按照放大倍数找到新的ABCD像素点的位置并进行对应的填充,但是它们之间存在的大量的像素点,比如p点的色彩值却是不可知的,需要进行估算。
图1-原始图像的相邻4个像素点分布图
图2-图像放大4倍后已知像素分布图
1、最临近点插值算法(Nearest Neighbor)
最邻近点插值算法是最简单也是速度最快的一种算法,其做法是將放大后未知的像素点P,將其位置换算到原始影像上,与原始的邻近的4周像素点A,B,C,D做比较,令P点的像素值等于最靠近的邻近点像素值即可。
如上图中的P点,由于最接近D点,所以就直接取P=D。
这种方法会带来明显的失真。
在A,B中点处的像素值会突然出现一个跳跃,这就是出现马赛克和锯齿等明显走样的原因。
最临近插值法唯一的优点就是速度快。
2、双线性插值算法(Bilinear Interpolation)
其做法是將放大后未知的像素点P,將其位置换算到原始影像上,计算的四個像素点A,B,C,D对P点的影响(越靠近P点取值越大,表明影响也越大),其示意图如下。
图3-双线性插值算法示意图
其具体的算法分三步:
第一步插值计算出AB两点对P点的影响得到e点的值。
图4-线性插值算法求值示意图
对线性插值的理解是这样的,对于AB两像素点之间的其它像素点的色彩值,认定为直线变化的,要求e点处的值,只需要找到对应位置直线上的点即可。
换句话说,A,B间任意一点的值只跟A,B有关。
第二步,插值计算出CD两点对P点的影响得到f点的值。
第三步,插值计算出ef两点对P点的影响值。
双线性插值算法由于插值的结果是连续的,所以视觉上会比最邻近点插值算法要好一些,不过运算速度稍微要慢一点,如果讲究速度,是一个不错的折衷。
3、双立方插值算法(Bicubic Interpolation)
双立方插值算法与双线性插值算法类似,对于放大后未知的像素点P,将对其影响的范围扩大到邻近的16个像素点,依据对P点的远近影响进行插值计算,因P点的像素值信息来自16个邻近点,所以可得到较细致的影像,不过速度比较慢。
图5-双线性插值算法4个邻近点影响未知点信息示意图
图6-双立方插值算法16个邻近点影响未知点信息示意图
不过双立方插值算法与双线性插值算法的本质区别不仅在于扩大了影响点的范围,还采用高级的插值算法,如图所示。
图7-非线性插值算法求值示意图
要求A,B两点之间e点的值,需要利用A,B周围A-1,A,B,B+1四个点的像素值,通过某种非线性的计算,得到光滑的曲线,从而算出e点的值来。
所谓“双”或者叫“二次”的意思就是在计算了横向插值影响的基础上,把上述运算拓展到二维空间,再计算纵向插值影响的意思。
双立方插值算法能够得到相对清晰的画面质量,不过计算量也变大。
该算法在现在的众多图像处理软件中最为常用,比如Photoshop,After Effects,Avid,Final Cut Pro等。
为了得到更好的图像质量,在以上的基础上,许多新的算法不断涌现,它们使用了更加复杂的改进的插值方式。
譬如B样条(B-SPline), 米切尔(Mitchell)等插值算法,它们的目的是使插值的曲线显得更平
滑,图像边缘的表现更加完美。
4、自适应样条插值极其增强技术( S-Spline & S-Spline XL)
与上述经典的插值方法最大的区别在于, S-Spline 采用了一种自适应技术,那些传统的方法总是依据周围的像素点来求未知点的色彩值,也就是说需要求解的色彩值仅仅依靠该像素点在图像中的位置,而非实际的图像的像素信息,而自适应样条算法还会考虑实际图像的像素信息。
实验表明,经过 S-Spline 算法得到的图像效果要优于双立方插值算法。
现在 S-Spline 算法又出现了增强版 S-Spline XL,新版本的 S-Spline XL 算法较 S-Spline 而言画面的锐度得到进一步增强,物体的轮廓更加清晰,边缘的锯齿现象大大减弱,图像感受更加自然。
二、图像放大算法实际测试
现在我们来对以上几种插值算法进行实际测试,看看它们的效果。
首先打开原始的图像bird.jpg.这是一个分辨率为360×270的图像。
图8-原始图像
我们采用 BenVista 公司著名的 PhotoZoom Pro 2 软件,在pc电脑上进行测试,电脑的CPU配置为In ter Core 2 T5500 1.66GHz,分别采用以上5种插值方法把原始图像放大8倍得到5个2880×2160的图像。
图9-最临近点插值N earrst_ N eighbour
图10-双线性插值B ilinear
图11-双立方插值B icubic
图12-自适应样条插值S-S pline
图13-自适应样条增强性插值S-S pline_ XL
对比以上各图并结合实验数据,我把效果参数列举如下表。
插值类型主观感受图像轮廓总体评价处理耗时
最临近点插值
N earrst_ N eigh
bour
马赛克现象严重不清晰最差5秒
双线性插值B ilinear 图像模糊,不锐利
边缘不清晰,有锯齿
现象
差6秒
双立方插值
B icubic
图像较模糊,较锐利锯齿现象有所改善折中8秒
自适应样条插值S-S pline 图像相对清晰,锐利
边缘变得清晰,锯齿
现象消失
好18秒
自适应样条增强
S-S pline_ XL
图像清晰,锐利边缘锐利,清晰最好20秒
显然,为了得到最好的图像放大质量,在可选条件下,我们应该使用自适应样条插值增强(S-S pl ine_ XL)技术来放大图像。
