平面直角坐标系中的几何综合题
平面直角坐标系练习题及答案

平面直角坐标系练习题及答案6.1.2 平面直角坐标系基础过关作业1.点 P(3,2) 在第一象限。
2.如图,矩形 ABCD 中,A(-4,1),B(2,1),C(2,3),则点D 的坐标为(-4,3)。
3.以点 M(-3,0) 为圆心,以5为半径画圆,分别交 x 轴的正半轴,负半轴于 P、Q 两点,则点 P 的坐标为(4,0),点 Q 的坐标为(-2,0)。
4.点 M(-3,5) 关于 x 轴的对称点 M1 的坐标是(-3,-5);关于y 轴的对称点 M2 的坐标是(3,5)。
5.已知 x 轴上的点 P 到 y 轴的距离为3,则点 P 的坐标为(C) (0,3) 或 (0,-3)。
6.在平面直角坐标系中,点(-1,m2+1) 一定在第二象限。
7.在直角坐标系中,点 P(2x-6,x-5) 在第四象限中,则 x 的取值范围是(B) -3<x<5.8.如图,在所给的坐标系中描出下列各点的位置:A(-4,4)、B(-2,2)、C(3,-3)、D(5,-5)、E(-3,3)、F(0,0)。
这些点没有明显的关系。
综合创新作业9.(综合题) 在如图所示的平面直角坐标系中描出 A(2,3)、B(-3,-2)、C(4,1) 三点,并用线段将 A、B、C 三点依次连接起来,其面积为 12.5.10.如图,是儿童乐园平面图。
建立适当的平面直角坐标系,各娱乐设施的坐标为:滑梯(5,5)、秋千(2,2)、跷跷板(-3,-3)、摇摆(0,0)。
11.(创新题) 在平面直角坐标系中,画出点 A(0,2)、B(-1,0),过点 A 作直线 L1 ∥x轴,过点 B 作 L2 ∥y轴,分析 L1、L2上点的坐标特点,由此,可以总结出在平面直角坐标系中,如果一条直线平行于 x 轴,那么这条直线上的点的 y 坐标相等;如果一条直线平行于 y 轴,那么这条直线上的点的 x 坐标相等。
12.(1) 已知点 P1(a,3) 与 P2(-2,-3) 关于原点对称,则a=2.(2) 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是(D) (-2,-800)。
八年级坐标与几何综合题(压轴题)
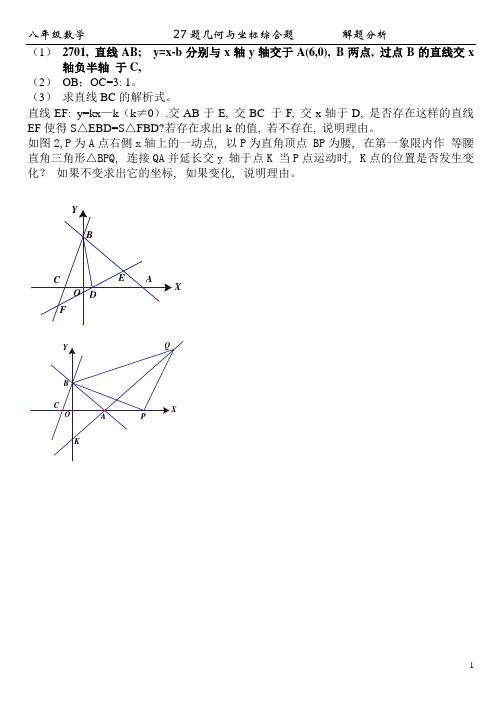
(1)2701, 直线AB; y=x-b分别与x轴y轴交于A(6,0), B两点, 过点B的直线交x 轴负半轴于C,(2)OB;OC=3: 1。
(3)求直线BC的解析式。
直线EF: y=kx—k(k≠0).交AB于E, 交BC 于F, 交x轴于D, 是否存在这样的直线EF使得S△EBD=S△FBD?若存在求出k的值, 若不存在, 说明理由。
如图2,P为A点右侧x轴上的一动点, 以P为直角顶点 BP为腰, 在第一象限内作等腰直角三角形△BPQ, 连接QA并延长交y 轴于点K 当P点运动时, K点的位置是否发生变化?如果不变求出它的坐标, 如果变化, 说明理由。
X(1)2702, 如图, 在平面直角坐标系中, 一次函数y=x+7与X轴, Y轴分别交与点A,C.点B为x轴正半轴上一点, 且△ABC的面积为70。
(2)求直线BC的解析式。
动点P从A 出发沿线段AB向点B以每秒2个单位的速度运动, 同时点Q从点C出发沿射线CO以每秒1个单位的速度匀速运动, 当点P停止运动时点Q也停止运动。
连接PO,PC,设△ABC的面积为S, 点P,Q的运动时间为t(秒), 求S与t的函数关系式, 并直接写出自变量的取值范围。
在(2)的条件下, 在直线BC上是否存在点D, 连接DP,DO.使得△DPQ是以PQ为直角边的等腰直角三角形, 若存在求出t值, 若不存在, 说明理由。
2703.在平面直角坐标系中, 直线y=x-4与X轴, Y轴分别交于A, D两点, AB⊥AD, 交y轴于点B 。
(1)求直线AB 的解析式。
(2)点P 为X 轴上一动点, PC ⊥PB, 交直线AD 于点C, 设 △PAC 的面积为S, 点P 的横坐标为t, 求S 与t 的函数关系式, 并写出自变量t 的取值范围。
(3)在(2)的条件下, 当S=2.5时, 求t 的值。
2704, 在平面直角坐标系中, 正比例函数y=x 的图像上有一点P (点P 在第一象限), 点A 为Y轴上的一动点, PB⊥PA, 交X轴正半轴与点B, PH⊥X轴。
函数与几何综合问题(共25题)(学生版)--2023年中考数学真题分项汇编(全国通用)

专题32函数与几何综合问题(25题)一、填空题1(2023·四川眉山·统考中考真题)如图,在平面直角坐标系xOy中,点B的坐标为-8,6,过点B分别作x轴、y轴的垂线,垂足分别为点C、点A,直线y=-2x-6与AB交于点D.与y轴交于点E.动点M在线段BC上,动点N在直线y=-2x-6上,若△AMN是以点N为直角顶点的等腰直角三角形,则点M的坐标为2(2023·四川自贡·统考中考真题)如图,直线y=-13x+2与x轴,y轴分别交于A,B两点,点D是线段AB上一动点,点H是直线y=-43x+2上的一动点,动点E m,0,F m+3,0,连接BE,DF,HD.当BE+DF取最小值时,3BH+5DH的最小值是.3(2023·江苏无锡·统考中考真题)二次函数y=a(x-1)(x-5)a>1 2的图像与x轴交于点A、B,与y轴交于点C,过点M3,1的直线将△ABC分成两部分,这两部分是三角形或梯形,且面积相等,则a 的值为.二、解答题4(2023·黑龙江牡丹江·统考中考真题)如图,在平面直角坐标系中,▱ABCD的顶点B,C在x轴上,D在y轴上,OB,OC的长是方程x2-6x+8=0的两个根(OB>OC).请解答下列问题:(1)求点B 的坐标;(2)若OD :OC =2:1,直线y =-x +b 分别交x 轴、y 轴、AD 于点E ,F ,M ,且M 是AD 的中点,直线EF 交DC 延长线于点N ,求tan ∠MND 的值;(3)在(2)的条件下,点P 在y 轴上,在直线EF 上是否存在点Q ,使△NPQ 是腰长为5的等腰三角形?若存在,请直接写出等腰三角形的个数和其中两个点Q 的坐标;若不存在,请说明理由.5(2023·湖南·统考中考真题)如图,点A ,B ,C 在⊙O 上运动,满足AB 2=BC 2+AC 2,延长AC 至点D ,使得∠DBC =∠CAB ,点E 是弦AC 上一动点(不与点A ,C 重合),过点E 作弦AB 的垂线,交AB 于点F ,交BC 的延长线于点N ,交⊙O 于点M (点M 在劣弧AC上).(1)BD 是⊙O 的切线吗?请作出你的判断并给出证明;(2)记△BDC ,△ABC ,△ADB 的面积分别为S 1,S 2,S ,若S 1⋅S =S 2 2,求tan D 2的值;(3)若⊙O 的半径为1,设FM =x ,FE ⋅FN ⋅1BC ⋅BN +1AE ⋅AC=y ,试求y 关于x 的函数解析式,并写出自变量x 的取值范围.6(2023·湖南·统考中考真题)我们约定:若关于x 的二次函数y 1=a 1x 2+b 1x +c 1与y 2=a 2x 2+b 2x +c 2同时满足a 2-c 1+(b 2+b 1)2+c 2-a 1 =0,b 1-b 22023≠0,则称函数y 1与函数y 2互为“美美与共”函数.根据该约定,解答下列问题:(1)若关于x 的二次函数y 1=2x 2+kx +3与y 2=mx 2+x +n 互为“美美与共”函数,求k ,m ,n 的值;(2)对于任意非零实数r ,s ,点P r ,t 与点Q s ,t r ≠s 始终在关于x 的函数y 1=x 2+2rx +s 的图像上运动,函数y 1与y 2互为“美美与共”函数.①求函数y 2的图像的对称轴;②函数y 2的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;(3)在同一平面直角坐标系中,若关于x 的二次函数y 1=ax 2+bx +c 与它的“美美与共”函数y 2的图像顶点分别为点A ,点B ,函数y 1的图像与x 轴交于不同两点C ,D ,函数y 2的图像与x 轴交于不同两点E ,F .当CD =EF 时,以A ,B ,C ,D 为顶点的四边形能否为正方形?若能,求出该正方形面积的取值范围;若不请说明理由.7(2023·江苏无锡·统考中考真题)如图,四边形ABCD 是边长为4的菱形,∠A =60°,点Q 为CD 的中点,P 为线段AB 上的动点,现将四边形PBCQ 沿PQ 翻折得到四边形PB C Q .(1)当∠QPB =45°时,求四边形BB C C 的面积;(2)当点P 在线段AB 上移动时,设BP =x ,四边形BB C C 的面积为S ,求S 关于x 的函数表达式.8(2023·江苏徐州·统考中考真题)如图,在平而直角坐标系中,二次函数y =-3x 2+23x 的图象与x 轴分别交于点O ,A ,顶点为B .连接OB ,AB ,将线段AB 绕点A 按顺时针方向旋转60°得到线段AC ,连接BC .点D ,E 分别在线段OB ,BC 上,连接AD ,DE ,EA ,DE 与AB 交于点F ,∠DEA =60°.(1)求点A ,B 的坐标;(2)随着点E 在线段BC 上运动.①∠EDA 的大小是否发生变化?请说明理由;②线段BF 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;(3)当线段DE 的中点在该二次函数的因象的对称轴上时,△BDE 的面积为.9(2023·内蒙古·统考中考真题)如图,在平面直角坐标系中,抛物线y =-x 2+3x +1交y 轴于点A ,直线y =-13x +2交抛物线于B ,C 两点(点B 在点C 的左侧),交y 轴于点D ,交x 轴于点E .(1)求点D ,E ,C 的坐标;(2)F 是线段OE 上一点OF <EF ,连接AF ,DF ,CF ,且AF 2+EF 2=21.①求证:△DFC 是直角三角形;②∠DFC 的平分线FK 交线段DC 于点K ,P 是直线BC 上方抛物线上一动点,当3tan ∠PFK =1时,求点P 的坐标.10(2023·吉林·统考中考真题)如图,在正方形ABCD 中,AB =4cm ,点O 是对角线AC 的中点,动点P ,Q 分别从点A ,B 同时出发,点P 以1cm/s 的速度沿边AB 向终点B 匀速运动,点Q 以2cm/s 的速度沿折线BC -CD 向终点D 匀速运动.连接PO 并延长交边CD 于点M ,连接QO 并延长交折线DA -AB 于点N ,连接PQ ,QM ,MN ,NP ,得到四边形PQMN .设点P 的运动时间为x (s )(0<x <4),四边形PQMN 的面积为y (cm 2)(1)BP 的长为cm ,CM 的长为cm .(用含x 的代数式表示)(2)求y 关于x 的函数解析式,并写出自变量x 的取值范围.(3)当四边形PQMN 是轴对称图形时,直接写出x 的值.11(2023·广东·统考中考真题)综合运用如图1,在平面直角坐标系中,正方形OABC 的顶点A 在x 轴的正半轴上,如图2,将正方形OABC 绕点O 逆时针旋转,旋转角为α0°<α<45° ,AB 交直线y =x 于点E ,BC 交y 轴于点F .(1)当旋转角∠COF 为多少度时,OE =OF ;(直接写出结果,不要求写解答过程)(2)若点A (4,3),求FC 的长;(3)如图3,对角线AC 交y 轴于点M ,交直线y =x 于点N ,连接FN ,将△OFN 与△OCF 的面积分别记为S 1与S 2,设S =S 1-S 2,AN =n ,求S 关于n 的函数表达式.12(2023·湖北黄冈·统考中考真题)已知抛物线y =-12x 2+bx +c 与x 轴交于A ,B (4,0)两点,与y 轴交于点C (0,2),点P 为第一象限抛物线上的点,连接CA ,CB ,PB ,PC .(1)直接写出结果;b =,c =,点A 的坐标为,tan ∠ABC =;(2)如图1,当∠PCB =2∠OCA 时,求点P 的坐标;(3)如图2,点D 在y 轴负半轴上,OD =OB ,点Q 为抛物线上一点,∠QBD =90°,点E ,F 分别为△BDQ 的边DQ ,DB 上的动点,QE =DF ,记BE +QF 的最小值为m .①求m 的值;②设△PCB 的面积为S ,若S =14m 2-k ,请直接写出k 的取值范围.13(2023·湖北宜昌·统考中考真题)如图,已知A (0,2),B (2,0).点E 位于第二象限且在直线y =-2x 上,∠EOD =90°,OD =OE ,连接AB ,DE ,AE ,DB .(1)直接判断△AOB 的形状:△AOB 是三角形;(2)求证:△AOE ≌△BOD ;(3)直线EA 交x 轴于点C (t ,0),t >2.将经过B ,C 两点的抛物线y 1=ax 2+bx -4向左平移2个单位,得到抛物线y 2.①若直线EA 与抛物线y 1有唯一交点,求t 的值;②若抛物线y 2的顶点P 在直线EA 上,求t 的值;③将抛物线y 2再向下平移,2(t -1)2个单位,得到抛物线y 3.若点D 在抛物线y 3上,求点D 的坐标.14(2023·山东滨州·统考中考真题)如图,在平面直角坐标系中,菱形OABC 的一边OC 在x 轴正半轴上,顶点A 的坐标为2,23 ,点D 是边OC 上的动点,过点D 作DE ⊥OB 交边OA 于点E ,作DF ∥OB 交边BC 于点F ,连接EF .设OD =x ,△DEF 的面积为S .(1)求S 关于x 的函数解析式;(2)当x 取何值时,S 的值最大?请求出最大值.15(2023·天津·统考中考真题)在平面直角坐标系中,O 为原点,菱形ABCD 的顶点A (3,0),B (0,1),D (23,1),矩形EFGH 的顶点E 0,12 ,F -3,12 ,H 0,32.(1)填空:如图①,点C 的坐标为,点G 的坐标为;(2)将矩形EFGH 沿水平方向向右平移,得到矩形E F G H ,点E ,F ,G ,H 的对应点分别为E ,F ,G ,H .设EE =t ,矩形E F G H 与菱形ABCD 重叠部分的面积为S .①如图②,当边E F 与AB 相交于点M 、边G H 与BC 相交于点N ,且矩形E F G H 与菱形ABCD 重叠部分为五边形时,试用含有t 的式子表示S ,并直接写出t 的取值范围:②当233≤t ≤1134时,求S 的取值范围(直接写出结果即可).16(2023·浙江温州·统考中考真题)如图1,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆于点D ,BE ⊥CD ,交CD 延长线于点E ,交半圆于点F ,已知OA =32,AC =1.如图2,连接AF ,P 为线段AF 上一点,过点P 作BC 的平行线分别交CE ,BE 于点M ,N ,过点P 作PH ⊥AB 于点H .设PH =x ,MN =y .(1)求CE 的长和y 关于x 的函数表达式.(2)当PH <PN ,且长度分别等于PH ,PN ,a 的三条线段组成的三角形与△BCE 相似时,求a 的值.(3)延长PN 交半圆O 于点Q ,当NQ =154x -3时,求MN 的长.17(2023·新疆·统考中考真题)【建立模型】(1)如图1,点B 是线段CD 上的一点,AC ⊥BC ,AB ⊥BE ,ED ⊥BD ,垂足分别为C ,B ,D ,AB =BE .求证:△ACB ≌△BDE ;【类比迁移】(2)如图2,一次函数y =3x +3的图象与y 轴交于点A 、与x 轴交于点B ,将线段AB 绕点B 逆时针旋转90°得到BC 、直线AC 交x 轴于点D .①求点C 的坐标;②求直线AC 的解析式;【拓展延伸】(3)如图3,抛物线y =x 2-3x -4与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于C点,已知点Q (0,-1),连接BQ .抛物线上是否存在点M ,使得tan ∠MBQ =13,若存在,求出点M 的横坐标.18(2023·江苏连云港·统考中考真题)【问题情境 建构函数】(1)如图1,在矩形ABCD 中,AB =4,M 是CD 的中点,AE ⊥BM ,垂足为E .设BC =x ,AE =y ,试用含x 的代数式表示y .【由数想形 新知初探】(2)在上述表达式中,y 与x 成函数关系,其图像如图2所示.若x 取任意实数,此时的函数图像是否具有对称性?若有,请说明理由,并在图2上补全函数图像.【数形结合 深度探究】(3)在“x 取任意实数”的条件下,对上述函数继续探究,得出以下结论:①函数值y 随x 的增大而增大;②函数值y 的取值范围是-42<y <42;③存在一条直线与该函数图像有四个交点;④在图像上存在四点A 、B 、C 、D ,使得四边形ABCD 是平行四边形.其中正确的是.(写出所有正确结论的序号)【抽象回归 拓展总结】(4)若将(1)中的“AB=4”改成“AB=2k”,此时y关于x的函数表达式是;一般地,当k≠0,x取任意实数时,类比一次函数、反比例函数、二次函数的研究过程,探究此类函数的相关性质(直接写出3条即可).19(2023·四川凉山·统考中考真题)阅读理解题:阅读材料:如图1,四边形ABCD是矩形,△AEF是等腰直角三角形,记∠BAE为α、∠FAD为β,若tanα=1 2,则tanβ=13.证明:设BE=k,∵tanα=12,∴AB=2k,易证△AEB≌△EFC AAS∴EC=2k,CF=k,∴FD=k,AD=3k∴tanβ=DFAD =k3k=13,若α+β=45°时,当tanα=12,则tanβ=13.同理:若α+β=45°时,当tanα=13,则tanβ=12.根据上述材料,完成下列问题:如图2,直线y=3x-9与反比例函数y=mx(x>0)的图象交于点A,与x轴交于点B.将直线AB绕点A顺时针旋转45°后的直线与y轴交于点E,过点A作AM⊥x轴于点M,过点A作AN⊥y轴于点N,已知OA=5.(1)求反比例函数的解析式;(2)直接写出tan ∠BAM 、tan ∠NAE 的值;(3)求直线AE 的解析式.20(2023·山东泰安·统考中考真题)如图1,二次函数y =ax 2+bx +4的图象经过点A (-4,0),B (-1,0).(1)求二次函数的表达式;(2)若点P 在二次函数对称轴上,当△BCP 面积为5时,求P 坐标;(3)小明认为,在第三象限抛物线上有一点D ,使∠DAB +∠ACB =90°;请判断小明的说法是否正确,如果正确,请求出D 的坐标;如果不正确,请说明理由.21(2023·湖北恩施·统考中考真题)在平面直角坐标系xoy 中,O 为坐标原点,已知抛物线y =-12x 2+bx +c 与y 轴交于点A ,抛物线的对称轴与x 轴交于点B .(1)如图,若A 0,3 ,抛物线的对称轴为x =3.求抛物线的解析式,并直接写出y ≥3时x 的取值范围;(2)在(1)的条件下,若P 为y 轴上的点,C 为x 轴上方抛物线上的点,当△PBC 为等边三角形时,求点P ,C 的坐标;(3)若抛物线y =-12x 2+bx +c 经过点D m ,2 ,E n ,2 ,F 1,-1 ,且m <n ,求正整数m ,n 的值.22(2023·辽宁营口·统考中考真题)如图,抛物线y =ax 2+bx -1a ≠0 与x 轴交于点A 1,0 和点B ,与y 轴交于点C ,抛物线的对称轴交x 轴于点D 3,0 ,过点B 作直线l ⊥x 轴,过点D 作DE ⊥CD ,交直线l 于点E .(1)求抛物线的解析式;(2)如图,点P为第三象限内抛物线上的点,连接CE和BP交于点Q,当BQPQ=57时.求点P的坐标;(3)在(2)的条件下,连接AC,在直线BP上是否存在点F,使得∠DEF=∠ACD+∠BED?若存在,请直接写出点F的坐标;若不存在,请说明理由.23(2023·山东日照·统考中考真题)在平面直角坐标系xOy内,抛物线y=-ax2+5ax+2a>0交y 轴于点C,过点C作x轴的平行线交该抛物线于点D.(1)求点C,D的坐标;(2)当a=13时,如图1,该抛物线与x轴交于A,B两点(点A在点B的左侧),点P为直线AD上方抛物线上一点,将直线PD沿直线AD翻折,交x轴于点M(4,0),求点P的坐标;(3)坐标平面内有两点E1a ,a+1,F5,a+1,以线段EF为边向上作正方形EFGH.①若a=1,求正方形EFGH的边与抛物线的所有交点坐标;②当正方形EFGH的边与该抛物线有且仅有两个交点,且这两个交点到x轴的距离之差为52时,求a的值.24(2023·江苏无锡·统考中考真题)已知二次函数y=22x2+bx+c的图像与y轴交于点A,且经过点B(4,2)和点C(-1,2).(1)请直接写出b,c的值;(2)直线BC交y轴于点D,点E是二次函数y=22x2+bx+c图像上位于直线AB下方的动点,过点E作直线AB的垂线,垂足为F.①求EF的最大值;②若△AEF中有一个内角是∠ABC的两倍,求点E的横坐标.25(2023·辽宁·统考中考真题)如图,抛物线y=-12x2+bx+c与x轴交于点A和点B4,0,与y轴交于点C0,4,点E在抛物线上.(1)求抛物线的解析式;(2)点E在第一象限内,过点E作EF∥y轴,交BC于点F,作EH∥x轴,交抛物线于点H,点H在点E的左侧,以线段EF,EH为邻边作矩形EFGH,当矩形EFGH的周长为11时,求线段EH的长;(3)点M在直线AC上,点N在平面内,当四边形OENM是正方形时,请直接写出点N的坐标.11。
平面直角坐标系与几何图形的综合(解析版)

【期末复习】浙教版八年级上册提分专题:平面直角坐标系与几何图形的综合各问题归纳总结若点()11y x A ,、()22y x B ,、()b a P ,问题一:若点P 在x 轴上,则b=0; 若点P 在y 轴上,则a=0;若点P 在第一象限,则a >0,b >0; 若点P 在第二象限,则a <0,b >0; 若点P 在第三象限,则a <0,b <0; 若点P 在第四象限,则a >0,b <0;问题二:若点A 、B 在同一水平线上,则21y y =; 若点A 、B 在同一竖直线上,则21x x =; 若点P 在第一、三象限角平分线上,则b a =;若点P 在第二、四象限角平分线上,则b a -=;问题三:点()b a P ,关于x 轴对称的点P 1坐标为()b a P -,1; 点()b a P ,关于y 轴对称的点P 2坐标为()b a P ,-2;点()b a P ,关于原点对称的点P 3坐标为()b a P --,3; 问题四:点的平移口诀“左减右加,上加下减”; 问题五:线段AB 的中点公式:⎪⎭⎫⎝⎛++222121y y x x ,;若点A 、B 在同一水平线上,则AB=21x x -;若点A 、B 在同一竖直线上,则AB=21y y -;若点A 、B 所在直线是倾斜的,则AB=()()221221y y x x AB -+-=(两点间距离公式)问题六:点()b a P ,到x 轴的距离=|b|;点()b a P ,到y 轴的距离=|a|;问题七:割补法,优先分割,然后才是补全 问题八:周期型:①判断周期数(一般3到4个);②总数÷周期数=整周期……余数(余数是谁就和每周期的第几个规律一样) 注意横纵坐标的规律可能不同。
【类题训练】1.如图,A (8,0),B (0,6),以点A 为圆心,AC 长为半径画弧,交y 轴正半轴于点B ,则点C 的坐标为( )A .(10,0)B .(0,10)C .(﹣2,0)D .(0,﹣2)【分析】根据勾股定理求出AB ,根据坐标与图形性质解答即可. 【解答】解:由题意得,OB =6,OA =8, ∴AB ==10,则AC =10, ∴OC =AC ﹣OA =2, ∴点C 坐标为(﹣2,0), 故选:C .2.在平面直角坐标系中,点A 的坐标为(﹣1,3),点B 的坐标为(5,3),则线段AB 上任意一点的坐标可表示为( )A.(3,x)(﹣1≤x≤5)B.(x,3)(﹣1≤x≤5)C.(3,x)(﹣5≤x≤1)D.(x,3)(﹣5≤x≤1)【分析】根据A、B两点纵坐标相等,可确定AB与x轴平行,即可求解.【解答】解:∵点A的坐标为(﹣1,3),点B的坐标为(5,3),A、B两点纵坐标都为3,∴AB∥x轴,∴线段AB上任意一点的坐标可表示为(x,3)(﹣1≤x≤5),故选:B.3.如图,在四边形ABCD中,AD∥BC∥x轴,下列说法中正确的是()A.点A与点D的纵坐标相同B.点A与点B的横坐标相同C.点A与点C的纵坐标相同D.点B与点D的横坐标相同【分析】根据与x轴平行的直线上点的坐标特征计算判断.【解答】解:∵平行四边形ABCD中,AD∥BC∥x轴,∴点A与D的纵坐标相同,点B与C的纵坐标相同.故选:A.4.如图,已知∠AOB=30°,∠AOC=60°,∠AOD=90°,∠AOE=120°,∠AOF=150°,若点B可表示为点B(2,30),点C可表示为点C(1,60),点E可表示为点E(3,120),点F可表示为点F(4,150),点B 可表示为点B(2,30),则D点可表示为()A.D(0,90)B.D(90,0)C.D(90,5)D.D(5,90)【分析】根据题干得出规律,从而得出答案.【解答】解:根据题意知:横坐标表示长度,纵坐标表示角度,从而得出D点可表示为(5,90),故选:D.5.在平面直角坐标系中,若A(m+3,m﹣1),B(1﹣m,3﹣m),且直线AB∥x轴,则m的值是()A.﹣1B.1C.2D.3【分析】根据平行于x轴的直线上的点的纵坐标相等,建立方程求解即可求得答案.【解答】解:∵直线AB∥x轴,∴m﹣1=3﹣m,解得:m=2,故选:C.6.如图,在平面直角坐标系中,半径均为1个单位长度的半圆组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2022秒时,点P的坐标是()A.(2021,0)B.(2022,﹣1)C.(2021,﹣1)D.(2022,0)【分析】利用坐标与图形的关系,结合路程问题求解.【解答】解:一个半圆的周长是π,速度是每秒,所以走一个半圆需要2秒,2022秒正好可以走1011个半圆,故选:D.7.如图,在平面直角坐标系中,点A(1,1),B(3,1),C(3,3),D(1,3),动点P从点A出发,以每秒1个单位长度的速度沿AB﹣BC﹣CD﹣DA﹣AB﹣…路线运动,当运动到2022秒时,点P的坐标为()A.(1,1)B.(3,1)C.(3,3)D.(1,3)【分析】利用路程找规律,看最后的路脚点,再求解.【解答】解:由题意得:四边形ABCD是正方形,且边长是2,点P运动一周需要8秒,2022÷8商252余6,结果到点D处,故坐标为(1,3),故选:D.8.如图,在平面直角坐标系中,三角形ABC三个顶点A、B、C的坐标A(0,4),B(﹣1,b),C(2,c),BC 经过原点O,且CD⊥AB,垂足为点D,则AB•CD的值为()A.10B.11C.12D.14【分析】AB•CD可以联想到△ABC的面积公式,根据S△ABO+S△ACO=S△ABC即可求解.【解答】解:∵A(0,4),∴OA=4,∵B(﹣1,b),C(2,c),∴点B,C到y轴的距离分别为1,2,∵S△ABO+S△ACO=S△ABC,∴×4×1+×4×2=×AB•CD,∴AB•CD=12,故答案为:C.9.如图,在平面直角坐标系中,A,B,C三点坐标分别为(0,a),(0,3﹣a),(1,2),且点A在点B的下方,连接AC,BC,若在AB,BC,AC若所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为5个,那么a的取值范围是()A.﹣1<a≤0B.﹣1≤a≤1C.1≤a<2D.0<a≤1【分析】根据题意得出除了点C外,其它三个横纵坐标为整数的点落在所围区域的边界上,即线段AB上,从而求出a的取值范围.【解答】解:∵点A(0,a),点B(0,3﹣a),且A在B的下方,∴a<3﹣a,解得:a<1.5,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为5个,∵点A,B,C的坐标分别是(0,a),(0,3﹣a),(1,2),∴区域内部(不含边界)没有横纵坐标都为整数的点,∴已知的5个横纵坐标都为整数的点都在区域的边界上,∵点C(1,2)的横纵坐标都为整数且在区域的边界上,∴其他的4个都在线段AB上,∴3≤3﹣a<4.解得:﹣1<a≤0,故选:A.10.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为()A.(2,2)B.(,)C.(2,)D.(,)【分析】过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2,故OD=4﹣2,即B′点的坐标为(2,).【解答】解:过点B′作B′D⊥OC∵∠CPB=60°,CB′=OC=OA=4∴∠B′CD=30°,B′D=2根据勾股定理得DC=2∴OD=4﹣2,即B′点的坐标为(2,)故选:C.11.如图,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a﹣3),则a的值为.【分析】根据作图方法可知点P在∠BOA的角平分线上,由角平分线的性质可知点P到x轴和y轴的距离相等,可得关于a的方程,求解即可.【解答】解:∵OA=OB,分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P,∴点P在∠BOA的角平分线上,∴点P到x轴和y轴的距离相等,又∵点P的坐标为(a,2a﹣3),∴a=2a﹣3,∴a=3.故答案为:3.12.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是.【分析】因为△ABD与△ABC有一条公共边AB,故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论,计算即可得出答案.【解答】解:△ABD与△ABC有一条公共边AB,当点D在AB的下边时,点D有两种情况:①坐标是(4,﹣1);②坐标为(﹣1,﹣1);当点D在AB的上边时,坐标为(﹣1,3);点D的坐标是(4,﹣1)或(﹣1,3)或(﹣1,﹣1).13.教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,有两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),如:点A(1,2)、点B(3,6),则线段AB的中点M 的坐标为(,),即M(2,4).利用以上结论解决问题:平面直角坐标系中,若E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于y轴上,且到x轴的距离是1,则4a+b的值等于.【分析】根据中点坐标公式求出点G的坐标,根据线段EF的中点G恰好位于y轴上,且到x轴的距离是1,得到点G的横坐标等于0,纵坐标的绝对值为1,列出方程组求解即可.【解答】解:根据题意得:G(,),∵线段EF的中点G恰好位于y轴上,且到x轴的距离是1,∴,解得:4a+b=4或0.故答案为:4或0.14.在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”给出如下定义:若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|,例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).已知点,B为y轴上的一个动点.(1)若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;(2)直接写出点A与点B的“非常距离”的最小值.【分析】(1)根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|0﹣y|=2,据此可以求得y的值;(2)设点B的坐标为(0,y).因为|﹣﹣0|≥|0﹣y|,所以点A与点B的“非常距离”最小值为|﹣﹣0|=.【解答】解:(1)∵B为y轴上的一个动点,∴设点B的坐标为(0,y).∵|﹣﹣0|=≠4,∴|0﹣y|=2,解得y=2或y=﹣2;∴点B的坐标是(0,2)或(0,﹣2);故答案为:(0,2)或(0,﹣2);(2)∵|﹣﹣0|≥|0﹣y|,∴点A与点B的“非常距离”最小值为|﹣﹣0|=;∴点A与点B的“非常距离”的最小值为.故答案为:.15.如图,在平面直角坐标系中,已知三点的坐标分别为A(0,4),B(2,0),C(2,5),连接AB,AC,BC.(1)求AC,AB的长;(2)∠CAB是直角吗?请说明理由.【分析】(1 )过点A作AH⊥BC于点H,再利用勾股定理求解即可;(2 )利用勾股定理的逆定理即可得出结论.【解答】解:(1)如图,∵A(0,4),B(2,0),C(2,5),∴OA=4,OB=2,BC=5,过点A作AH⊥BC于点H,∴BH=OA=4,AH=OB=2,∴CH=BC﹣BH=5﹣4=1,在Rt△OAB中,AB=,在Rt△ACH中,AC=;(2)∠CAB是直角,理由:由(1)得,AC=,AB=2,BC=5,∵,∴AC2+AB2=BC2,∴∠CAB是直角.16.对于某些三角形或四边形,我们可以直接用面积公式或者用割补法来求它们的面积.下面我们再研究一种求某些三角形或四边形面积的新方法:如图1,2所示,分别过三角形或四边形的顶点A,C作水平线的铅垂线l1,l2,l1,l2之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交AC于点D,称线段BD的长叫做这个三角形的铅垂高;如图2所示,分别过四边形的顶点B,D作水平线l3,l4,l3,l4之间的距离h叫做四边形的铅垂高.【结论提炼】容易证明:“三角形的面积等于水平宽与铅垂高乘积的一半”,即“S=dh”【结论应用】为了便于计算水平宽和铅垂高,我们不妨借助平面直角坐标系.已知:如图3,点A(﹣5,2),B(5,0),C(0,5),则△ABC的水平宽为10,铅垂高为,所以△ABC 面积的大小为.【再探新知】三角形的面积可以用“水平宽与铅垂高乘积的一半”来求,那四边形的面积是不是也可以这样求呢?带着这个问题,我们进行如下探索:(1)在图4所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(4,1),D(﹣2,﹣4)四个点,得到四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是;用其它的方法进行计算得到其面积的大小是,由此发现:用“S=dh”这一方法对求图4中四边形的面积.(填“适合”或“不适合”)(2)在图5所示的平面直角坐标系中,取A(﹣5,2),B(1,5),C(4,2),D(﹣2,﹣3)四个点,得到了四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是,用其它的方法进行计算得到面积的大小是,由此发现:用“S=dh”这一方法对求图5中四边形的面积.(“适合”或“不适合”)(3)在图6所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(5,1),D(﹣1,﹣5)四个点,得到了四边形ABCD.通过计算发现:用“S=dh”这一方法对求图6中四边形的面积.(填“适合”或“不适合”)【归纳总结】我们经历上面的探索过程,通过猜想、归纳,验证,便可得到:当四边形满足某些条件时,可以用“S=dh”来求面积.那么,可以用“S=dh”来求面积的四边形应满足的条件是:.【分析】【结论应用】直接代入公式即可;【再探新知】(1)求出水平宽,铅垂高,代入公式求出面积,再利用矩形面积减去周围四个三角形面积可得答案;(2)(3)与(1)同理;【归纳总结】当四边形满足一条对角线等于水平宽或铅垂高时,四边形可以用“S=dh”来求面积.【解答】解:【结论应用】由图形知,铅垂高为4,S△ABC==20,故答案为:4,20;【再探新知】(1)∵四边形ABCD的水平宽为8,铅垂高为9,∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小为36,利用四边形ABCD所在的矩形面积减去周围四个三角形面积为8×9﹣=37.5,∴用“S=dh”这一方法对求图4中四边形的面积不合适,故答案为:36,37.5,不合适;(2)∵四边形ABCD的水平宽为9,铅垂高为8,∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小为36,利用四边形ABCD所在的矩形面积减去周围四个三角形面积为8×9﹣=36,∴用“S=dh”这一方法对求图4中四边形的面积,合适,故答案为:36,36,合适;(3)∵四边形ABCD的水平宽为9,铅垂高为10,∴运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小为45,利用四边形ABCD所在的矩形面积减去周围四个三角形面积为10×9﹣=45,∴用“S=dh”这一方法对求图4中四边形的面积,合适,故答案为:合适;【归纳总结】当四边形满足一条对角线等于水平宽或铅垂高时,四边形可以用“S=dh”来求面积,故答案为:一条对角线等于水平宽或铅垂高.17.如图所示,在平面直角坐标系中,P(2,2),(1)点A在x的正半轴运动,点B在y的正半轴上,且P A=PB,①求证:P A⊥PB;②求OA+OB的值;(2)点A在x的正半轴运动,点B在y的负半轴上,且P A=PB,③求OA﹣OB的值;④点A的坐标为(8,0),求点B的坐标.【分析】(1)①过点P作PE⊥x轴于E,作PF⊥y轴于F,根据点P的坐标可得PE=PF=2,然后利用“HL”证明Rt△APE和Rt△BPF全等,根据全等三角形对应角相等可得∠APE=∠BPF,然后求出∠APB=∠EPF=90°,再根据垂直的定义证明;②根据全等三角形对应边相等可得AE=BF,再表示出OA、OB,然后列出方程整理即可得解;(2)③根据全等三角形对应边相等可得AE=BF,再表示出PE、PF,然后列出方程整理即可得解;④求出AE的长度,再根据全等三角形对应边相等可得AE=BF,然后求出OB,再写出点B的坐标即可.【解答】(1)①证明:如图1,过点P作PE⊥x轴于E,作PF⊥y轴于F,∵P(2,2),∴PE=PF=2,在Rt△APE和Rt△BPF中,,∴Rt△APE≌Rt△BPF(HL),∴∠APE=∠BPF,∴∠APB=∠APE+∠BPE=∠BPF+∠BPE=∠EPF=90°,∴P A⊥PB;②解:∵Rt△APE≌Rt△BPF,∴BF=AE,∵OA=OE+AE,OB=OF﹣BF,∴OA+OB=OE+AE+OF﹣BF=OE+OF=2+2=4;(2)解:③如图2,∵Rt△APE≌Rt△BPF,∴AE=BF,∵AE=OA﹣OE=OA﹣2,BF=OB+OF=OB+2,∴OA﹣2=OB+2,∴OA﹣OB=4;④∵PE=PF=2,PE⊥x轴于E,作PF⊥y轴于F,∴四边形OEPF是正方形,∴OE=OF=2,∵A(8,0),∴OA=8,∴AE=OA﹣OE=8﹣2=6,∵Rt△APE≌Rt△BPF,∴AE=BF=6,∴OB=BF﹣OF=6﹣2=4,∴点B的坐标为(0,﹣4).18.如图,在平面直角坐标系xOy中,点B(1,0),点C(5,0),以BC为边在x轴的上方作正方形ABCD,点M(﹣5,0),N(0,5).(1)点A的坐标为;点D的坐标为;(2)将正方形ABCD向左平移m个单位,得到正方形A'B'C'D',记正方形A'B'C'D'与△OMN重叠的区域(不含边界)为W:①当m=3时,区域内整点(横,纵坐标都是整数)的个数为;②若区域W内恰好有3个整点,请直接写出m的取值范围.【分析】(1)先求出正方形的边长为BC=4,再求点的坐标即可;(2)①画出正方形A'B'C'D',结合图形求解即可;②在△OMN中共有6个整数点,在平移正方形ABCD,找到恰好有3个整数解的情况即可.【解答】解:(1)∵点B(1,0),点C(5,0),∴BC=4,∵四边形ABCD是正方形,∴A(1,4),D(5,4),故答案为:(1,4),(5,4);(2)①如图:共有3个,故答案为:3;②在△OMN中共有6个整数点,分别是(﹣1,1),(﹣1,2),(﹣1,3),(﹣2,1),(﹣2,2),(﹣3,1),∵区域W内恰好有3个整点,∴2<m≤3或6≤m<7.19.类比学习是知识内化的有效途径,认真读题是正确审题的第一步:对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(其中k为常数,且k≠0),则称点P'为点P的“k系好友点”;例如:P(1,2)的“3系好友点”为即.请完成下列各题.(1)点P(﹣3,1)的“2系好友点”P'的坐标为.(2)若点P在y轴的正半轴上,点P的“k系好友点”为P'点,若在三角形OPP'中,pp′=3OP,求k的值.(3)已知点A(x,y)在第四象限,且满足xy=﹣8;点A是点B(m,n)的“﹣2系好友点”,求m﹣2n的值.【分析】(1)根据“k系好友点”的定义列式计算求解;(2)设P(0,t)(t>0),根据定义得点P′(kt,t),则PP′=|kt|=3OP=3t,即可求解;(3)点A是点B(m,n)的“﹣2系好有点”,可得点A(m﹣2n,n﹣),由xy=﹣8得到(m﹣2n)2=16,即可求解.【解答】解:(1)点P(﹣3,1),根据“k系好友点”的求法可知,k=2,∵﹣3+2×1=﹣1,1+=﹣,∴P′的坐标为(﹣1,﹣),故答案为(﹣1,﹣);(2)设P(0,t)其中t>0,根据“k系好友点”的求法可知,P′(kt,t),∴PP'∥x轴,∴PP'=|kt|,又∵OP=t,PP'=3OP,∴|kt|=3t,∴k=±3;(3)∵B(m,n)的﹣3系好有点A为(m﹣2n,n﹣),∴x=m﹣2n,y=n﹣,又∵xy=﹣8,∴(m﹣2n)•(n﹣)=﹣8,∴m﹣2n=±4,∵点A在第四象限,∴x>0,即m﹣2n=4.20.如图,在以点O为原点的平面直角坐标系中点A,B的坐标分别为(a,0),(a,b),点C在y轴上,且BC∥x轴,a,b满足|a﹣3|+=0.点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到O为止).(1)直接写出点A,B,C的坐标;(2)当点P运动3秒时,连接PC,PO,求出点P的坐标,并直接写出∠CPO,∠BCP,∠AOP之间满足的数量关系;(3)点P运动t秒后(t≠0),是否存在点P到x轴的距离为t个单位长度的情况.若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)利用绝对值和二次根式的非负性即可求得;(2)当P运动3秒时,点P运动了6个单位长度,根据AO=3,即可得点P在线段AB上且AP=3,写出P 的坐标即可;作PE∥AO.利用平行线的性质证明即可;(3)由t≠0得点P可能运动到AB或BC或OC上.再分类讨论列出一元一次方程解得t即可.【解答】解:(1)∵|a﹣3|+=0且|a﹣3|≥0,≥0,∴|a﹣3|=0,=0,∴a=3,b=4,∴A(3,0),B(3,4),C(0,4);(2)如图,当P运动3秒时,点P运动了6个单位长度,∵AO=3,∴点P运动3秒时,点P在线段AB上,且AP=3,∴点P的坐标是(3,3);如图,作PE∥AO.∵CB∥AO,PE∥AO,∴CB∥PE,∴∠BCP=∠EPC,∠AOP=∠EPO,∴∠CPO=∠BCP+∠AOP;(3)存在.∵t≠0,∴点P可能运动到AB或BC或OC上.①当点P运动到AB上时,2t≤7,∵0<t≤,P A=2t﹣OA=2t﹣3,∴2t﹣3=t,解得:t=2,∴P A=2×2﹣3=1,∴点P的坐标为(3,1);②当点P运动到BC上时,7≤2t≤10,即≤t≤5,∵点P到x轴的距离为4,∴t=4,解得t=8,∵≤t≤5,∴此种情况不符合题意;③当点P运动到OC上时,10≤2t≤14,即5≤t≤7,∵PO=OA+AB+BC+OC﹣2t=14﹣2t,∴14﹣2t=t,解得:t=,∴PO=﹣2×+14=,∴点P的坐标为(0,).综上所述,点P运动t秒后,存在点P到x轴的距离为t个单位长度的情况,点P的坐标为(3,1)或(0,).。
初中七年级数学《平面直角坐标系中几何综合题》

七年级下学期期末备考之《平面直角坐标系中几何综合题》一.解答题(共17小题)1.(春•玉环县期中)如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.(1)求a、b的值;(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.(标注:三角形ABC的面积表示为S△ABC)②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.2.(春•汕头校级期中)如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+=0.(1)求a、b、c的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.3.(春•鄂城区期中)如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=+﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.4.(春•富顺县校级期末)在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2)(见图1),且|2a+b+1|+=0(1)求a、b的值;(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积仍然成立?若存在,请直接写出符合条件的点M的坐标;(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,的值是否会改变?若不变,求其值;若改变,说明理由.5.(春•泰兴市校级期末)已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP 上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线l∥PQ,点D在点C的左边且CD=3.(1)直接写出△BCD的面积.(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,求证:∠CEF=∠CFE.(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中的值是否变化?若不变,求出其值;若变化,求出变化范围.6.(春•江岸区期末)如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.(1)求点A、B的坐标.(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图2,求∠AMD的度数.(3)如图3,(也可以利用图1)①求点F的坐标;②点P为坐标轴上一点,若△ABP的三角形和△ABC的面积相等?若存在,求出P点坐标.7.(春•黄陂区期末)在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组,c为y轴正半轴上一点,且S△ABC=6.(1)求A、B、C三点的坐标;(2)是否存在点P(t,t),使S△PAB=S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;(3)若M是AC的中点,N是BC上一点,CN=2BN,连AN、BM相交于点D,求四边形CMDN的面积是.8.(春•海珠区期末)在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.(1)求点A和点B的坐标;(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.9.(春•黄梅县校级期中)如图,在下面的直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式.(1)求a,b的值;(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.10.(春•通州区校级期中)在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式+(b﹣3)2=0,(c﹣4)2≤0.(1)求a、b、c的值;(2)如果点P(m,n)在第二象限,四边形CBOP的面积为y,请你用含m,n的式子表示y;(3)如果点P在第二象限坐标轴的夹角平分线上,并且y=2S四边形CBOA,求P点的坐标.11.(春•鄂州校级期中)如图,A、B两点坐标分别为A(a,4),B(b,0),且a,b满足(a﹣2b+8)2+=0,E是y轴正半轴上一点.(1)求A、B两点坐标;(2)若C为y轴上一点且S△AOC=S△AOB,求C点的坐标;(3)过B作BD∥y轴,∠DBF=∠DBA,∠EOF=∠EOA,求∠F与∠A间的数量关系.12.(春•东湖区期中)如图,平面直角坐标系中A(﹣1,0),B(3,0),现同时将A、B 分别向上平移2个单位,再向右平移1个单位,分别得到A、B的对应点C、D,连接AC、BD(1)直接写出C、D的坐标:C D及四边形ABCD的面积:(2)在y轴负半轴上是否存在点M,连接MA、MB使得S△MAB>S四边形ABCD?若存在,求出M点纵坐标的取值范围;若不存在说明理由(3)点P为线段BD上一动点,连PC、PO,当点P在BD上移动(不含端点)现给出①的值不变,②的值不变,其中有且只有一个正确,请你找出这个结论并求其值.13.(春•台州月考)如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.14.(春•海安县月考)如图,在平面直角坐标系中,点A,B,C的坐标分别为(﹣1,0),(3,0),(0,2),图中的线段BD是由线段AC平移得到.(1)线段AC经过怎样的平移可得到线段BD,所得四边形是什么图形,并求出所得的四边形ABDC的面积S四边形ABDC;(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在,求出点P的坐标;若不存在,试说明理由;(3)点P是线段BD上的一个动点,连接PC、PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①的值不变;②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.15.(春•武汉月考)已知,在平面直角坐标系中,点A(0,m),点B(n,0),m、n满足(m﹣3)2=﹣;(1)求A、B的坐标;(2)如图1,E为第二象限内直线AB上一点,且满足S△AOE=S△AOB,求E的坐标.(3)如图2,平移线段BA至OC,B与O是对应点,A与C对应,连AC.E为BA的延长线上一动点,连EO.OF平分∠COE,AF平分∠EAC,OF交AF于F点.若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F(用含α的式子表示).16.(2013秋•江岸区校级月考)如图,已知点A(﹣m,n),B(0,m),且m、n满足+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.(1)写出D点坐标并求A、D两点间的距离;(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.17.(2013春•武汉校级月考)如图,在平面直角坐标系中,点A,B的坐标分别为A(﹣1,0)、B(3,0).现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C、D,连接AC,BD.(1)直接写出点C、D的坐标,求四边形ABDC的面积S四边形ABDC;(2)在坐标轴上是否存在一点P,使S△PAC=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.(3)如图3,在线段CO上取一点G,使OG=3CG,在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积S四边形OGHF.。
七(下)培优训练(三)平面直角坐标系综合问题(压轴题)

培优训练三:平面直角坐标系(压轴题)一、坐标与面积:【例1】如图,在平面直角坐标中,A (0,1),B (2,0),C (2,1.5). (1)求△AB C的面积;(2)如果在第二象限内有一点P(a ,0.5),试用a 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在这样的点P ,使四边形ABOP 的面积与△AB C的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.yxPOCBA【例2】在平面直角坐标系中,已知A (-3,0),B (-2,-2),将线段AB 平移至线段CD .图1y xDO CB A图2y xDOCB AyxOBAyxOBA(1)如图1,直接写出图中相等的线段,平行的线段;(2)如图2,若线段AB 移动到CD ,C 、D 两点恰好都在坐标轴上,求C 、D 的坐标;(3)若点C 在y 轴的正半轴上,点D在第一象限内,且S△ACD =5,求C、D 的坐标;(4)在y 轴上是否存在一点P ,使线段AB 平移至线段PQ 时,由A 、B 、P、Q 构成的四边形是平行四边形面积为10,若存在,求出P 、Q的坐标,若不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A (1,0),B (-2,3),C (-3,0).(1)求△ABC 的面积;(2)若把△AB C向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C '''; (3)若点A、C的位置不变,当点P 在y 轴上什么位置时,使2ACPABCS S=;(4)若点B 、C的位置不变,当点Q在x 轴上什么位置时,使2BCQABCS S=.【例4】如图1,在平面直角坐标系中,A (a ,0),C (b,2),且满足2(2)20a b ++-=,过C 作CB ⊥x 轴于B.(1)求三角形ABC 的面积;(2)若过B作BD ∥AC 交y 轴于D,且AE ,D E分别平分∠CA B,∠ODB ,如图2,求∠AE D的度数;(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形A CP 的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.【例5】如图,在平面直角坐标系中,四边形AB CD 各顶点的坐标分别是A(0,0),B(7,0),C (9,5),D (2,7)(1)在坐标系中,画出此四边形; (2)求此四边形的面积;(3)在坐标轴上,你能否找一个点P ,使S △PBC =50, 若能,求出P 点坐标,若不能,说明理由.【例6】如图,A点坐标为(-2, 0), B 点坐标为(0, -3). (1)作图,将△ABO沿x轴正方向平移4个单位, 得到△DEF , 延长ED 交y 轴于C点, 过O点作O G⊥C E, 垂足为G ;(2) 在(1)的条件下, 求证: ∠C OG =∠E DF ; (3)求运动过程中线段A B扫过的图形的面积.【例7】在平面直角坐标系中,点B (0,4),C(-5,4),点A 是x轴负半轴上一点,S四边形A OBC =24.图1yxHOFEDAC B(1)线段B C的长为 ,点A的坐标为 ;(2)如图1,EA 平分∠CAO ,DA 平分∠CA H,CF ⊥A E点F,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线C B与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON平分AOP ∠,BN 交ON 于N,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由. 【例8】在平面直角坐标系中,OA=4,O C=8,四边形ABC O是平行四边形.A(-2,0)B(0,-3)y x 0(1)求点B 的坐标及的面积ABCO S 四边形;(2)若点P 从点C以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQ B与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,若存在,求出t 的值,若不存在,试说明理由;(3)在(2)的条件下,四边形Q BPO 的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.【例9】如图,在平面直角坐标系中,点A ,B的坐标分别为(-1,0),(3,0),现同时将点A,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A,B 的对应点C,D 连结AC ,B D. (1)求点C ,D 的坐标及四边形ABD C的面积S 四边形ABDC ;(2)在y轴上是否存在一点P ,连结P A ,PB ,使S △PAB =S △明理由;(3)若点Q自O 点以0.5个单位/s 的速度在线段AB上移动,运动到B点就停止,设移动的时间为t 秒,(1)是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?(4)是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?【例10】在直角坐标系中,△AB C的顶点A (—2,0),B (2,4),C (5,0). (1)求△ABC 的面积(2)点D 为y负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点F (5,n )是第一象限内一点,,连BF ,CF ,G 是x轴上一点,若△ABG 的面积等于四边形ABDC 的面积,则点G 的坐标为 (用含n 的式子表示)二、坐标与几何:【例1】如图,已知A (0,a),B (0,b),C (m ,b)且(a -4)2+|b+3|=0,S △ABC =14. (1)求C点坐标(2)作DE ⊥DC,交y 轴于E点,EF 为∠AED 的平分线,且∠DF E=900.求证:FD 平分∠ADO;(3)E 在y 轴负半轴上运动时,连E C,点P为A C延长线上一点,EM 平分∠AEC,且PM ⊥EM,PN ⊥x 轴于N点,PQ 平分∠APN,交x轴于Q点,则E 在运动过程中,错误!的大小是否发生变化,若不变,求出其值.【例2】如图,在平面直角坐标系中,已知点A(-5,0),B(5.0),D(2,7), (1)求C点的坐标;(2)动点P 从B 点出发以每秒1个单位的速度沿BA 方向运动,同时动点Q从C 点出发也以每秒1位的速度沿y轴正半轴方向运动(当P 点运动到A 点时,两点都停止运动)。
函数与几何综合问题专练2023中考真题分类汇编(共25题)(解析版)

专题32函数与几何综合问题(25题)一、填空题1.(2023·四川眉山·统考中考真题)如图,在平面直角坐标系xOy 中,点B 的坐标为()86-,,过点B 分别作x 轴、y 轴的垂线,垂足分别为点C 、点A ,直线26y x =--与AB 交于点D .与y 轴交于点E .动点M 在线段BC 上,动点N 在直线26y x =--上,若AMN 是以点N 为直角顶点的等腰直角三角形,则点M 的坐标为【答案】()8,6M -或28,3M ⎛⎫- ⎪⎝⎭【分析】如图,由AMN 是以点N 为直角顶点的等腰直角三角形,可得N 在以AM 为直径的圆H 上,MN AN =,可得N 是圆H 与直线26y x =--的交点,当,M B 重合时,符合题意,可得()8,6M -,当N 在AM 的上方时,如图,过N 作NJ y ⊥轴于J ,延长MB 交BJ 于K ,则90NJA MKN ∠=∠=︒,8JK AB ==,证明MNK NAJ ≌,设(),26N x x --,可得MK NJ x ==-,266212KN AJ x x ==---=--,而8KJ AB ==,则2128x x ---=,再解方程可得答案.【详解】解:如图,∵AMN 是以点N 为直角顶点的等腰直角三角形,∴N 在以AM 为直径的圆H 上,MN AN =,∴N 是圆H 与直线26y x =--的交点,当,M B 重合时,∵()8,6B -,则()4,3H -,∴4MH AH NH ===,符合题意,∴()8,6M -,当N 在AM 的上方时,如图,过N 作NJ y ⊥轴于J ,延长MB 交BJ 于K ,则90NJA MKN ∠=∠=︒,8JK AB ==,∴90NAJ ANJ ∠+∠=︒,【答案】392【分析】作出点()32C -,,作CD 直角三角形求得1103F ⎛⎫ ⎪⎝⎭,,利用待定系数法求得直线DG y ⊥轴于点G ,此时35BH +【详解】解:∵直线123y x =-+则2CP =,3OP =,∵CFP AFD ∠=∠,∴FCP FAD ∠=∠,∴tan tan FCP FAD ∠=∠,∴PF OB PC OA=,即226PF =,∴23PF =,则1103F ⎛⎫ ⎪⎝⎭,,设直线CD 的解析式为y kx =+则321103k b k b +=-⎧⎪⎨+=⎪⎩,解得311k b =⎧⎨=-⎩∴直线CD 的解析式为3y x =联立,311123y x y x =-⎧⎪⎨=-+⎪⎩,解得⎧⎪⎪⎨⎪⎪⎩即3971010D ⎛⎫ ⎪⎝⎭,;过点D 作DG y ⊥轴于点G ,②如图2,直线BM过AC中点,直线BM解析式为1522y x=-+,AC中点坐标为910a=;③如图3,直线CM过AB中点,AB中点坐标为()3,0,5⑤如图5,直线ME ∥AC ,MN CO ∥,则EMN ACO∽∴12BE AB =,又4AB =,∴22BE =,∵53222BN =-=<,∴不成立;⑥如图6,直线ME ∥BC ,同理可得12AE AB =,∴22AE =,222NE =-,tan tan MEN CBO ∠∠=,∴155222a =-,解得212a +=;综上所述,910a =或225+或212+.【点睛】本题考查了二次函数的综合问题,解直角三角形,相似三角形的性质与判定,熟练掌握以上知识,并分类讨论是解题的关键.二、解答题4.(2023·黑龙江牡丹江·统考中考真题)如图,在平面直角坐标系中,ABCD Y 的顶点B ,C 在x 轴上,D(1)求点B 的坐标;(2)若:2:1OD OC =,直线y x b =-+分别交x DC 延长线于点N ,求tan MND ∠的值;(3)在(2)的条件下,点P 在y 轴上,在直线存在,请直接写出等腰三角形的个数和其中两个点【答案】(1)()4,0B -(2)1tan 3MND ∠=(3)存在,等腰三角形的个数是8个,1652Q ⎛- ⎝【分析】(1)解方程得到OB ,OC 的长,从而得到点(2)由:2:1OD OC =,2OC =,得4OD =线y x b =-+中,求得b 的值,从而得到直线的解析式,进而求得点45FEO ∠=︒.过点C 作CH EN ⊥于H ,过点::2:1DO OC NK CK ==,进而得到2NK CK =EC CK =,由211EC OC OE =-=-=可得CK 得到22cos EK EN KEN ==∠,在Rt ECH △中,322NH EN EH =-=,最终可得结果tan MND ∠(3)分PN PQ =,PN NQ =,PQ NQ =三大类求解,共有【详解】(1)解方程2680x x -+=,得14x =OB OC > ,(3)解:由(2)知:直线EF 解析式为设()0,P p ,(),1Q q q -+,①当5PN QN ==时,()()2223025p -+--=,()23q -+解得6p =-或2p =,6522q +=或∴1652524,22Q ⎛⎫-- ⎪ ⎪⎝⎭,2652Q ⎛+ ⎝如图,11PQ N 、12PQ N 、21P Q N ;②当5PQ QN ==时,由①知:1652524,22Q ⎛⎫-- ⎪ ⎪⎝⎭,2652,2Q ⎛+ ⎝;③当5PN PQ ==时,由①知:()10,6P -,()20,2P ,当()10,6P -时,()()22061q q -+-+-解得13q =(舍去),24q =,∴()34,3Q -,如图,当()20,2P 时,()()220215q q -++-=解得13q =(舍去),24q =-,综上,等腰三角形的个数是8个,符合题意的Q 坐标为16525,2Q ⎛- ⎝【点睛】本题考查了一次函数的图像与性质,一次函数与平行四边形,等腰三角形的综合问题,数形结合思想是解题的关键.5.(2023·湖南·统考中考真题)如图,点使得DBC CAB ∠=∠,点E 是弦AC 上一动点(不与点交BC 的延长线于点N ,交O 于点M (1)BD 是O 的切线吗?请作出你的判断并给出证明;(2)记BDC ABC ADB ,,的面积分别为(3)若O 的半径为1,设FM x =,FE 自变量x 的取值范围.【答案】(1)BD 是O 的切线,证明见解析(2)152+∴在Rt OFM △中,2OF OM =∴211BF BO OF x =+=+-,AF2②若a c=,则A、B关于y轴对称,以综上,以A,B,C,D为顶点的四边形能构成正方形,此时【点睛】本题主要考查了二次函数的综合应用、正方形的性质等知识点,解题的关键是利用分类讨论的思想解决问题.(1)当45QPB ∠=︒时,求四边形(2)当点P 在线段AB 上移动时,设【答案】(1)438+(2)23234312x S x =++【分析】(1)连接BD 、可得PBQ 为等腰直角三角形,则 四边形ABCD 为菱形,∠PB x=,23BQ=,PBQ(1)求点,A B 的坐标;(2)随着点E 在线段BC 上运动.①EDA ∠的大小是否发生变化?请说明理由;②线段BF 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由;(3)当线段DE 的中点在该二次函数的因象的对称轴上时,【答案】(1)()20A ,,()13B ,;∵()2313y x =--+,∴抛物线对称轴为1x =,即1ON =,∵将线段AB 绕点A 按顺时针方向旋转∵2OA OB AC BC ====,∴四边形OACB 是菱形,∴BC OA ∥,∵DH BN ⊥,AN BN ⊥,∴DH BC OA ∥∥,∴MBE MHD ∠∠=,MEB MDH ∠∠=∵DE 的中点为点M ,∴MD ME =,∴MBE MHD ≌,∴DH BE =,∵90ANM ∠=︒,∴1809090MBE ANM ∠∠=︒-︒=︒=,∵DE 的中点为点M ,DAE 是等边三角形,∴AM DE ⊥,∴90AME ∠=︒,∴180BME NMA ∠∠+=︒,∴BME NAM ∠∠=,(1)求点,,D E C 的坐标;(2)F 是线段OE 上一点()OF EF <,连接,AF DF ①求证:DFC △是直角三角形;②DFC ∠的平分线FK 交线段DC 于点,K P 是直线坐标.【答案】(1)(3,1)C ,(0,2)D ,(6,0)E (2)①证明见解析,②点P 的坐标为(1,3)或(7,3【分析】(1)根据一次函数与坐标轴的交点及一次函数与二次函数的交点求解即可;(2)①设(,0),F m 然后利用勾股定理求解,m-①抛物线231y x x =-++交y 轴于点A ,当0x =时,1,y =.(0,1),A ∴1OA ∴=,在Rt AOF 中,90AOF ∠=︒,由勾股定理得222AF OA OF +=,设(,0),F m ,OF m ∴=221AF m ∴=+,(6,0),E .6,OE ∴=6EF OE OF m ∴=-=-,2221,AF EF += 221(6)21,m m ∴++-=122,4m m ∴==,,OF EF < 2,m ∴=2OF ∴=,(2,0)F ∴.(0,2),D 2OD ∴=,OD OF ∴=.DOF ∴ 是等腰直角三角形,45OFD ∴∠=︒.过点C 作CG x ⊥轴,垂足为G .(3,1),C 1,3CG OG ∴==,1,GF OG OF =-= ,CG GF ∴=CGF ∴ 是等腰直角三角形,45,GFC ∴∠︒=90,DFC ∴∠=︒DFC ∴ 是直角三角形.②FK 平分,90,DFC DFC ∠∠=︒(1)BP 的长为__________,CM 的长为_________(2)求y 关于x 的函数解析式,并写出自变量x 的取值范围.(3)当四边形PQMN 是轴对称图形时,直接写出x 【答案】(1)()4x -;x(2)()(241216024162x x y x x ⎧-+⎪=⎨-+<≤⎪⎩(3)43x =或83x =【分析】(1)根据正方形中心对称的性质得出OM ANP CQM ≌即可;(2)分02x <≤,2<两种情况分别画出图形,根据正方形的面积,以及平行四边形的性质即可求解;(3)根据(2)的图形,分类讨论即可求解.【详解】(1)解:依题意,1AP x x =⨯=()cm ,则∵四边形ABCD 是正方形,∴,90AD BC DAB ∠=∠=︒∥,∵点O 是正方形对角线的中点,∴,OM OP OQ ON ==,则四边形PQMN 是平行四边形,∴MQ PN =,MQ NP ∥∴PNQ MQN ∠=∠,又AD BC ∥,∴ANQ CQN ∠=∠,∴ANP MQC ∠=∠,在,ANP CQM 中,ANP MQC NAP QCM NP MQ ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ANP CQM ≌,∴()cm MC AP x ==故答案为:()4x -;x .(2)解:当02x <≤时,点Q 在BC 上,由(1)可得ANP CQM ≌,同理可得PBQ MDN ≌,∵4,2,PB x QB x MC x =-==,42QC x =-,则222MCQ BPQy AB S S =-- ()()164242x x x x =--⨯--241216x x =-+;当24x <≤时,如图所示,则AP x =,224AN CQ x CB x ==-=-,()244PN AP AN x x x =-=--=-+,∴()44416y x x =-+⨯=-+;综上所述,()()2412160241624x x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩;当四边形PQMN 是菱形时,则∴()()2242x x x -+=解得:0x =(舍去)②如图所示,当PB =424x x -=-,解得x 当四边形PQMN 是菱形时,则综上所述,当四边形【点睛】本题考查了正方形的性质,动点问题,全等三角形的性质与判定,矩形的性质,平行四边形的性质与判定,菱形的性质,轴对称图形,熟练掌握以上知识是解题的关键.(1)当旋转角COF ∠为多少度时,OE OF =;(直接写出结果,不要求写解答过程)(2)若点(4,3)A ,求FC 的长;(3)如图3,对角线AC 交y 轴于点M ,交直线y x =于点N ,连接FN ,将OFN △1S 与2S ,设12S S S =-,AN n =,求S 关于n 的函数表达式.【答案】(1)22.5︒(2)154FC =(3)212S n =【分析】(1)根据正方形的性质及直角三角形全等的判定及性质得出AOG ∠=45EOG ∠=︒,即可求解;(2)过点A 作AP x ⊥轴,根据勾股定理及点的坐标得出5OA =,再由相似三角形的判定和性质求解即可;(3)根据正方形的性质及四点共圆条件得出O 、C 、F 、N 四点共圆,再由圆周角定理及等腰直角三角形的判定和性质得出FN ON =,90FNO ∠=︒,过点N 作GQ BC ⊥于点G ,交OA 于点形的判定和性质得出,CG OQ CO QG ==,结合图形分别表示出1S ,2S ,得出(2)过点A 作AP x ⊥轴,如图所示:∵(4,3)A ,∴3,4AP OP ==,∴5OA =,∵正方形OABC ,∴5OC OA ==,90C ∠=∴90C APO ∠∠==︒,∵AOP COF ∠∠=,∴OCF OPA ∽ ,∴OC FC OP AP=即543FC =,∴154FC =;(3)∵正方形OABC ,∵BC OA ∥,∴GQ OA ⊥,∵90FNO ∠=︒,∴1290∠∠+=︒,∵1390∠∠+=︒,∴23∠∠=,∴(AAS)FGN NQO ≌ ∴,GN OQ FG QN ==,∵GQ BC ⊥,FCO COQ ∠∠=∴四边形COQG 为矩形,∴,CG OQ CO QG ==,∴(211S S ON OQ ===(1)直接写出结果;b =_____,c =_____,点A 的坐标为_____,tan ABC ∠=______(2)如图1,当2PCB OCA ∠=∠时,求点P 的坐标;(3)如图2,点D 在y 轴负半轴上,OD OB =,点Q 为抛物线上一点,90QBD ∠=︒,点的边,DQ DB 上的动点,QE DF =,记BE Q F +的最小值为m .①求m 的值;②设PCB 的面积为S ,若214S m k =-,请直接写出k 的取值范围.【答案】(1)32,2,()1,0-,12(2)()2,3(3)解:①如图2,作DH ⊥∵90BQD BDQ ︒∠+∠=,HDF ∠∴QD HDF ∠=∠,∵QE DF =,DH BQ =,∴(SAS)BQE HDF ≌,∴BE FH =,∴BE QF FH QF QH +=+≥,∴Q ,F ,H 共线时,BE Q F +②如图3,作PT y ∥轴,交设22,1T a a ⎛⎫-+ ⎪⎝⎭,,P a ⎛ ⎝则21132222S a a ⎛=-+++ ⎝∴04S <≤,∴21044m k <-≤,∴0174k <-≤,∴1317k ≤<.【点睛】本题考查用待定系数法求函数解析式、二次函数与几何综合、二次函数与(1)直接判断AOB 的形状:AOB 是_________三角形;(2)求证:AOE BOD △≌△;(3)直线EA 交x 轴于点(,0),2C t t >.将经过B ,C 两点的抛物线21y ax =物线2y .①若直线EA 与抛物线1y 有唯一交点,求t 的值;②若抛物线2y 的顶点P 在直线EA 上,求t 的值;③将抛物线2y 再向下平移,22(1)t -个单位,得到抛物线3y .若点D 在抛物线【答案】(1)等腰直角三角形(2)详见解析(3)①3t =;②6t =;③126,55D ⎛⎫ ⎪⎝⎭【分析】(1)由(0,2),(2,0)A B 得到2OA OB ==,又由90AOB ∠=︒,即可得到结论;(2)由90EOD ∠=︒,90AOB ∠=︒得到AOE BOD ∠=∠,又有AO OB =AOE BOD △≌△;(3)①求出直线AC 的解析式和抛物线1y 的解析式,联立得()23x t -+22(3)43(3)0t t t ∆=+-⨯=-=即可得到t 的值;∵90EOD ∠=︒,90AOB ∠=︒,AOB AOD DOE ∴∠-∠=∠-∠AOE BOD ∴∠=∠,∵,AO OB OD OE ==,(SAS)AOE BOD ∴△≌△;(3)①设直线AC 的解析式为(0,2),(,0)A C t ,∴90EMO OND ∠=∠=︒,90DOE ∠=︒ ,∴EOM MEO EOM NOD ∠+∠=∠+∠∴MEO NOD ∠=∠,∵OD OE =,∴(AAS)ODN EOM ≌,∴,ON EM DN OM ==,∵OE 的解析式为2y x =-,∴设22EM OM m ==,∴DN OM m ==,EM x ⊥ 轴,∴OA EM ∥,∴~CAO CEM ,::OC CM OA EM ∴=,22t t m m∴=+,1t m t ∴=-,∴2221t EM ON OM m t ====-,DN 2,11t t D t t ⎛⎫∴ ⎪--⎝⎭, 抛物线2y 再向下平移22(1)t -个单位,得到抛物线2222(2)y x t x(1)求S 关于x 的函数解析式;(2)当x 取何值时,S 的值最大?请求出最大值.【答案】(1)23232S x x =-+(2)当2x =时,S 的最大值为23∵顶点A 的坐标为()2,23,∴()222234OA =+=,2OG =,∴1cos 2OG AOG AO ∠==,①如图②,当边E F ''与AB 相交于点M 、边G H ''与BC 相交于点N ,且矩形E F G H ''''与菱形为五边形时,试用含有t 的式子表示S ,并直接写出t 的取值范围:②当2311334t ≤≤时,求S 的取值范围(直接写出结果即可).【答案】(1)()3,2,33,2⎛⎫- ⎪⎝⎭(2)①332t <≤;②3316S ≤≤【分析】(1)根据矩形及菱形的性质可进行求解;(2)①由题意易得3,1EF E F EH E H ''''====,然后可得60ABO ∠=︒,则有32EM =,进而根据割补∵四边形ABCD 是菱形,且(3,0),(0,1),(2A B D ∴()()2230012AB AD ==-+-=,AC BD ⊥∴2AC =,∴()3,2C ,故答案为()3,2,33,2⎛⎫- ⎪⎝⎭;(2)解:①∵点10,2E ⎛⎫ ⎪⎝⎭,点13,2F ⎛⎫- ⎪⎝⎭,点∴矩形EFGH 中,EF x ∥轴,EH x ⊥轴,EF ∴矩形E F G H ''''中,E F x ''∥轴,E H x ''⊥轴,由点()3,0A ,点()0,1B ,得3,1OA OB ==.在Rt ABO △中,tan 3OA ABO OB ∠==,得ABO ∠在Rt BME △中,由1tan 60,12EM EB EB =⋅︒=-此时面积S 最大,最大值为133S =⨯=当1134t =时,矩形E F G H ''''和菱形ABCD 由(1)可知B 、D 之间的水平距离为23,则有点由①可知:60D B ∠=∠=︒,(1)求CE的长和y关于x的函数表达式.(2)当PH PN<,且长度分别等于PH,PN,a的三条线段组成的三角形与(3)延长PN交半圆O于点Q,当1534NQ x=-时,求【答案】(1)165CE=,25412y x=-+(2)1615或2740或6041(3)17 8【分析】(1)如图1,连接OD,根据切线的性质得出出165CE=;证明四边形APMC是平行四边形,得出MN(2)根据BCE三边之比为3:4:5,可分为三种情况.当:3:4PH PN=时,分别列出比例式,进而即可求解.∵CD 切半圆O 于点D ,∴OD CE ⊥.∵32OA =,1AC =,∴52OC =,∴2CD =.∵BE CE ⊥,∴OD BE ∥,∴CD CO CE CB=,即5224CE =,∴165CE =.∵MN CB ∥,∴四边形APMC 是平行四边形,∴sin 1sin PH PH CM PA ===∠∵MN ME BC CE =,则90AQB AGQ ∠=∠=︒,∴QAB BQG ∠=∠.∵1534NQ x =-,PN y =。
八年级数学上册第5章平面直角坐标系专题训练13直角坐标系中几何问题习题课件新版苏科版

1
2
3
4
5
6
7
8
9
解:作A'H⊥ y 轴于 H ,则∠OHA'=90°.
∵ B (2,0),∴ OB =2.由旋转可得△A'OB'是等边三角形
且OB'= OB =2.∴OA'=OB'=2.
∵A'H⊥OB',∴ OH =HB'=1,
∴A'H= ′ − = − = ,∴A'(- ,
(3)如图③所示, PD = OD =5,点 P 在点 D 的右侧.过点
P 作 PE ⊥ x 轴于点 E ,则 PE =4.在Rt△ PDE 中,由勾股
定理得 DE = − = − =3,∴ OE = OD
+ DE =5+3=8,∴此时点 P 的坐标为(8,4).综上所
垂直平分线交 x 轴于点 C ,则点 C 的坐标为
点拨:如图,连接 BC ,
设 OC = x ,
∵ A (8,0), B (0,4),
∴ OA =8, OB =4.
1
2
3
4
5
6
7
8
9
(3,0)
.
∵ CD 垂直平分 AB ,
∴ BC = AC =8- x .
∵∠ BOC =90°,∴ BC2= OB2+ OC2,
=2,∴此时点 P 的坐标为(2,4);
1
2
3
4
5
6
7
8
9
(2)如图②所示, OP = OD =5.过点 P 作 PE ⊥ x 轴于点
E ,则 PE =4.
在Rt△ POE 中,由勾股定理得 OE = − =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年七年级下学期期末备考之《平面直角坐标系中几何综合
题》
2015-06-15
一.解答题(共17小题)
1.(2015春•玉环县期中)如图在平面直角坐标系中,A(a,0),B(b,0),(﹣1,2).且|2a+b+1|+=0.
(1)求a、b的值;
(2)①在y轴的正半轴上存在一点M,使S△COM=S△ABC,求点M的坐标.(标注:三角形ABC的面积表示为S△ABC)
②在坐标轴的其他位置是否存在点M,使S△COM=S△ABC仍成立?若存在,请直接写出符合条件的点M的坐标.
2.(2015春•汕头校级期中)如图,在下面直角坐标系中,已知A(0,a),B(b,0),C (3,c)三点,其中a、b、c满足关系式:|a﹣2|+(b﹣3)2+=0.
(1)求a、b、c的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在负整数m,使四边形ABOP的面积不小于△AOP面积的两倍?若存在,求出所有满足条件的点P的坐标,若不存在,请说明理由.
3.(2015春•鄂城区期中)如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=+﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.
4.(2014春•富顺县校级期末)在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2)(见图1),且|2a+b+1|+=0
(1)求a、b的值;
(2)①在x轴的正半轴上存在一点M,使△COM的面积=△ABC的面积,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积仍然成立?若存
在,请直接写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,的值是否会改变?若不变,求其值;若改变,说明理由.
5.(2014春•泰兴市校级期末)已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C 作直线l∥PQ,点D在点C的左边且CD=3.
(1)直接写出△BCD的面积.
(2)如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,求证:∠CEF=∠CFE.(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长
线于点H,在点B运动过程中的值是否变化?若不变,求出其值;若变化,求出变化范围.
6.(2014春•江岸区期末)如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
(1)求点A、B的坐标.
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图2,求∠AMD的度数.
(3)如图3,(也可以利用图1)
①求点F的坐标;
②点P为坐标轴上一点,若△ABP的三角形和△ABC的面积相等?若存在,求出P点坐标.
7.(2014春•黄陂区期末)在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b 满足方程组,c为y轴正半轴上一点,且S△ABC=6.
(1)求A、B、C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=S△ABC?若存在,请求出P点坐标;若不存在,请
说明理由;
(3)若M是AC的中点,N是BC上一点,CN=2BN,连AN、BM相交于点D,求四边形CMDN的面积是.
8.(2014春•海珠区期末)在平面直角坐标系中,点A(a,b)是第四象限内一点,AB⊥y 轴于B,且B(0,b)是y轴负半轴上一点,b2=16,S△AOB=12.
(1)求点A和点B的坐标;
(2)如图1,点D为线段OA(端点除外)上某一点,过点D作AO垂线交x轴于E,交直线AB于F,∠EOD、∠AFD的平分线相交于N,求∠ONF的度数.
(3)如图2,点D为线段OA(端点除外)上某一点,当点D在线段上运动时,过点D作直线EF交x轴正半轴于E,交直线AB于F,∠EOD,∠AFD的平分线相交于点N.若记∠ODF=α,请用α的式子表示∠ONF的大小,并说明理由.
9.(2014春•黄梅县校级期中)如图,在下面的直角坐标系中,已知A(0,a),B(b,0),
C(b,4)三点,其中a,b满足关系式.
(1)求a,b的值;
(2)如果在第二象限内有一点P(m,),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
10.(2014春•通州区校级期中)在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式+(b﹣3)2=0,(c﹣4)2≤0.
(1)求a、b、c的值;
(2)如果点P(m,n)在第二象限,四边形CBOP的面积为y,请你用含m,n的式子表示y;
(3)如果点P在第二象限坐标轴的夹角平分线上,并且y=2S四边形CBOA,求P点的坐标.
11.(2014春•鄂州校级期中)如图,A、B两点坐标分别为A(a,4),B(b,0),且a,b 满足(a﹣2b+8)2+=0,E是y轴正半轴上一点.
(1)求A、B两点坐标;
(2)若C为y轴上一点且S△AOC=S△AOB,求C点的坐标;
(3)过B作BD∥y轴,∠DBF=∠DBA,∠EOF=∠EOA,求∠F与∠A间的数量关系.
12.(2014春•东湖区期中)如图,平面直角坐标系中A(﹣1,0),B(3,0),现同时将A、B分别向上平移2个单位,再向右平移1个单位,分别得到A、B的对应点C、D,连接AC、BD
(1)直接写出C、D的坐标:C D及四边形ABCD的面积:(2)在y轴负半轴上是否存在点M,连接MA、MB使得S△MAB>S四边形ABCD?若存在,求出M点纵坐标的取值范围;若不存在说明理由
(3)点P为线段BD上一动点,连PC、PO,当点P在BD上移动(不含端点)现给出
①的值不变,②的值不变,
其中有且只有一个正确,请你找出这个结论并求其值.
13.(2014春•台州月考)如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.
14.(2014春•海安县月考)如图,在平面直角坐标系中,点A,B,C的坐标分别为(﹣1,0),(3,0),(0,2),图中的线段BD是由线段AC平移得到.
(1)线段AC经过怎样的平移可得到线段BD,所得四边形是什么图形,并求出所得的四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在,求出点P的坐标;若不存在,试说明理由;
(3)点P是线段BD上的一个动点,连接PC、PO,当点P在BD上移动时(不与B,D重合)给出下列结论:
①的值不变;②的值不变,
其中有且只有一个是正确的,请你找出这个结论并求其值.
15.(2014春•武汉月考)已知,在平面直角坐标系中,点A(0,m),点B(n,0),m、n 满足(m﹣3)2=﹣;
(1)求A、B的坐标;
(2)如图1,E为第二象限内直线AB上一点,且满足S△AOE=S△AOB,求E的坐标.
(3)如图2,平移线段BA至OC,B与O是对应点,A与C对应,连AC.E为BA的延长线上一动点,连EO.OF平分∠COE,AF平分∠EAC,OF交AF于F点.若
∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F(用含α的式子表示).
16.(2013秋•江岸区校级月考)如图,已知点A(﹣m,n),B(0,m),且m、n满足+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
17.(2013春•武汉校级月考)如图,在平面直角坐标系中,点A,B的坐标分别为A(﹣1,0)、B(3,0).现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C、D,连接AC,BD.
(1)直接写出点C、D的坐标,求四边形ABDC的面积S四边形ABDC;
(2)在坐标轴上是否存在一点P,使S△PAC=S四边形ABDC?若存在这样一点,求出点P的
坐标;若不存在,试说明理由.
(3)如图3,在线段CO上取一点G,使OG=3CG,在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积S四边形OGHF.。
