第三章_单自由度机械系统动力学汇总案例

例题
某起吊重物用的电动葫芦的电动机，型号为Y90L-4，额定功率 PH=1.5kW，同步转速n0=1500r/min，额定转速nH=1410r/min，求 该电动机在额定转速附近的机械性能。
解：在加载过程中电动机角速度只在额定角速度附近波动，可采用 直线形式的机械特性
例题
电动机型号Y100L2-4，额定功率PH=3kW，同步转速n0=1500r/min， 额定转速nH=1420r/min，最大转矩与额定转速之比λ=MK/MH=2.2，推导出三 相异步电动机机械特性图中AC段的机械特性。
等效转化的原则 等效构件的等效质量或等效转动惯量具有的动能等于原机械系 统的总动能； 等效构件上作用的等效力或力矩产生的瞬时功率等于原机械系 统所有外力产生的瞬时功率之和。 把这种具有等效质量或等效转动惯量，其上作用有等效力或等 效力矩的等效构件称为原机械系统的等效动力学模型。 对于单自由度机械系统，只要确定了一个构件的运动，其他构 件的运动就随之确定，因此，通过研究等效构件的运动规律，就能 确定原机械系统的运动。
基本概念
1、等效构件 具有与原机械系统等效的质量或等效转动惯量、其上 作用有等效力或等效力矩，而且其运动与原机械系统相应 构件的运动保持相同的构件。 2、等效条件 (1) 等效构件所具有的动能等于原机械系统的总动能； (2) 等效构件的瞬时功率等于原机械系统的总瞬时功率。 3、等效参数 (1) 等效质量me，等效转动惯量Je； (2) 等效力Fe，等效力矩Me。
图a
图b
等效参数的确定
1．等效质量和等效转动惯量 等效质量和等效转动惯量可以根据等效原则—— 等效构件所具有的动能等于原机械系统的总动能来确 定。
2、等效力和等效力矩 等效力和等效力矩可以根据等效原则——等效力 或等效力矩产生的瞬时功率等于机械系统所有外力和 外力矩在同一瞬时的功率总和来确定。
（2）求等效转动惯量 加载前的等效转动惯量为
3、驱动力是速度的函数，例如一般的电动机，机械特性均表示为输
出力矩随角速度变化的曲线。
二、三相异步电动机的机械特性
如图所示，三相异步电动机的输出力矩随角速度变化的曲线，称 为机械特性。AC段的运转是稳定的，当外载荷加大而导致机械减速 时，输出力矩将增加，并与外载荷达到新的平衡。而AD段的运转是 不稳定的，而外载荷增加导致转速下降时，输出力矩也下降，更无法 与外载荷平衡，造成转速进一步下降，直至停车。因此三相异步电动 机应在AC段工作。点B是电动机的额定工作点。
§3.1 概 述
机械的真实运动规律是由作用于机械上的外力、各 构件的质量、尺寸及转动惯量等因素决定的，而研究机 械在外力作用下的真实运动则是机械动力学的基本问题 （机械动力学的正问题）。本章主要研究两个问题: 第一，研究单自由度机械系统在外力作用下的真实 运动规律，即机械系统的运动随时间的变化规律。掌握 通过建立动力学模型建立力与运动参数之间的运动微分 方程来研究真实运动规律的方法。
式中l为活动构件总数 动能也可以表示为
l
l
Ek
式中
1 2 J eq 2
J e [mi (
i 1
l
vSi 2 ) J Si ( i ) 2 ] q q
称为广义速度，是随时间变化的。 Je称为系统的等效转动惯量。 q
2、系统的势能 对刚体机械系统，不计构件的弹性变形和变形能，而且一般情 况下，由构件的重量产生的势能与动能相对数值也很小，因此拉格 朗日方程中的势能常常可以略去。 3、系统的广义力 设Fk（k=1,2，…，m）和Mj（j=1,2，…，n）分别为作用于机 械上的外力和外力矩，则这些力和力矩的功率为
式中：mi——构件i的质量； JSi——构件i相对于其质心的转动惯量； vSi——构件i质心的速度； ωi——构件i的角速度。 作平动的构件的动能只含上式的第一项，作绕质心的定轴转动 的构件则只含第二项。
机械系统全部构件的动能总和为
1 1 2 Ek Eki ( mi v 2 J Si i ) si 2 i 1 i 1 2
二、单自由度机械系统的动力学方程 单自由度系统只有一个广义坐标，用q表示。对主动构件做回转 运动这种一般情况，常将主动构件的转角选定为系统的广义坐标。 整个系统的能量和机械功均可表示为这个广义坐标的函数。 1、系统的动能 设机械系统中的第i个构件做一般平面运动，启动能Eki可表示为
Eki 1 1 2 mi v 2 J Si si i 2 2
2. 等效构件的角加速度
d d d d dt d dt d
二、等效转动惯量是常数，等效力矩是速度的函数时
以电动机驱动的鼓风机、搅拌机、离心泵以及车床等之类机械属于这种情况。这些 机器的驱动力是速度的函数，而生产阻力是常数或者是速度的函数，机器的速比是常 数。因此，其等效力矩仅仅是速度的函数，而等效转动惯量是常数，此时，用力矩形 式的运动方程式求解比较方便。
生产阻力的几种情况：
1、生产阻力为常数，例如起重机、轧钢机、刨床等。 2、生产阻力随位移而变化，例如活塞式的压缩机和泵、曲柄压力机 等。
3、生产阻力随速度而变化，例如鼓风机、离心泵、螺旋桨。
4、生产阻力随时间而变化，例如球磨机、揉面机等。
驱动力的几种情况：
1、驱动力是常数，例如以重锤作为驱动装置的情况； 2、驱动力是位移的函数，例如用弹簧作驱动件时；
五、等效转动惯量及其导数的计算
[m j 2 (vSjx vSjy ) J j ( ) ] q q j 1
l
由此式对q求导可得
dJe 2 l 3 [m j (vSjx aSjx vSjy aSjy ) J j j j ] j 1 dq q
d 2 dJe Je Me dt 2 d
M e ( ) M ed ( ) M er ( ) J e d / dt
d t t0 J e 0 M ( ) e d d t Je = （t） 0 M ( ) dt e
例题P72
§3.4 动力学方程式的求解
注意：关键是确定等效转动惯量和等效力矩的关系式（解析式、图表形式等）
一、等效转动惯量和等效力矩均为位置的函数
（Md=Md()，Mr=Mr()， Me=Me()，Je=Je()）
1. 等效构件的角速度
1 1 2 2 J e J e 0 M e d 0 2 2 1 1 t t 0时 ， 0 2 2 J e ( ) ( ) J e0 0 M e ( )d 0 2 2 0 , J e J e 0
四、动力学方程
另一种形式的动力学方程 根据动能定理，等效力矩所作的功W等于等效构件动能的增量，即
E W
若等效构件由转角 1运动到 2时，角速度相应的由 1 变为 2 ， 则上式可改写为 2 1 1 2 2 J e 22 J e11 M e d 1 2 2 该式称为能量形式的动力学方程 若等效构件作直线运动，其位移由S1变到S2时，角速度相应地由v1 变为v2，则 s2 1 1 2 2 me 2 v2 me1v1 Fe ds s1 2 2 该式称为力矩（力）形式的动力学方程
第二，研究机械运转速度波动产生的原因及其调节 方法。
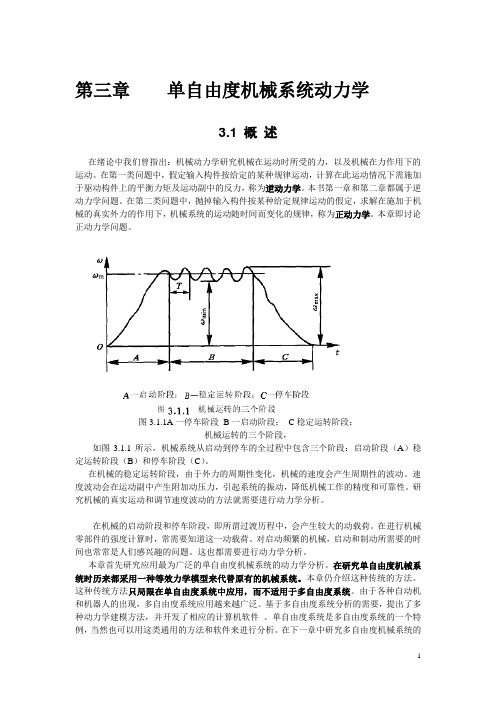
机械运转的三个阶段
1.启动阶段 原动件的速度由零逐渐上升到开始稳定的过程。 2.稳定运转阶段 1）周期变速稳定运转：角速度ω≠常数，产生周期性波动，会在运动副 中产生附加动反力，需进行动力学分析。 2）等速运转：ω=常数的稳定运转。 3.停车阶段 原动件的速度从正常工作速度下降到零的阶段。 在启动和制动阶段是会产生较大的动载荷，需进行动力学计算。
P ( Fk vk cos k ) ( M j j )
k 1 j 1 m n
式中：ωj——有外力矩Mj作用的构件的角速度； vk——外力Fk作用点的速度； αk——Fk与vk的夹角。 式中第二项符号的确定方法为：当Mj与ωj同向时取正号，反向时取负号。
广义力就是作用在广义坐标处的一个力或力矩，它所作的功等于系统中 全部力和力矩在同一时间内所作的功。
广义坐标为一个角位移时，广义力F为一等效力矩Me，它可按下式计算：
m j Fk vk cos k F Me ( ) ( M j ) q q k 1 j 1 m
、vk / q 是由机构的尺度和位置决定的， Me表示式中的广义传动比 j / q 的变化无关。 Me仅仅是机构广义坐标q的函数，与广义速度 q
等效动力学模型的建立
对于单自由度的机械系统，只要知道其中一个构件的运 动规律其余所有构件的运动规律就可随之求得。因此可把复 杂的机械系统简化成一个构件（称为等效构件),建立最简单 的等效动力学模型，将使研究机械真实运动的问题大为简化。 当等效构件为一个绕机架转动的构件时，模型为图a。当等效 构件为一个移动滑块时，模型为图b 。
1 G1 2 r 2 i g 1 20 (0.00715 0.15 2 0.00252 )kg.m 2 40 9.18 0.007256 kg.m 2 J e J1 J 2
加载后，还应加上重物的等效转动惯量
GR2 1 Je Je g r2 4000 0.12 1 (0.007256 2 )kg.m 2 9.81 40 0.009804 kg.m 2
§3.3 单自由度机械系统的动力学方程
一、拉格朗日方程 拉格朗日方程： Ek E p d Ek ( ) Fi (i 1,2,...,n) dt qi qi qi
式中：Ek——系统的动能； Ep——系统的势能； qi——广义坐标，它是可以完全确定机械系统运动的一组独立 参数； Fi——广义力，当广义坐标为一角位移时Fi为一个力矩，当广 义坐标为一线性位移时Fi为一个力； n——系统的广义坐标数。 利用拉格朗日方程进行系统的动力学分析时，先选定系统的广 义坐标，然后列出系统动能、势能和广义力的表达式，代入拉格朗 日方程中，即可导出系统的动力学方程。