高等数学中极限的几种求法分析及Matlab仿真
极限计算的13种方法示例

极限计算的13种方法示例极限是微积分中的重要概念,它描述了函数在某一点附近的行为。
在计算极限时,我们可以利用一些常见的方法来求解。
下面将介绍13种常见的极限计算方法。
一、代入法代入法是极限计算中最简单的方法之一。
当我们需要计算一个函数在某一点的极限时,只需要将该点的横坐标代入函数中,求得纵坐标即可。
二、夹逼定理夹逼定理是一种常用的极限计算方法,它适用于那些难以直接计算的函数。
夹逼定理的核心思想是通过找到两个函数,它们在极限点附近夹住我们要求的函数,从而求得该函数的极限值。
三、无穷小量法无穷小量法是极限计算中常用的方法之一。
它利用了无穷小量的性质,将函数中的高阶无穷小量忽略不计,只考虑最高阶的无穷小量来计算极限。
四、洛必达法则洛必达法则是一种常用的极限计算方法,它适用于求解0/0型和∞/∞型的极限。
该法则的核心思想是将函数的极限转化为两个函数的导数的极限,然后通过求导计算得到极限值。
五、泰勒展开法泰勒展开法是一种常用的近似计算极限的方法。
它利用了泰勒级数展开的性质,将函数在某一点附近进行泰勒展开,然后通过截断级数来计算函数的极限。
六、换元法换元法是一种常用的极限计算方法,它适用于那些存在复杂变量关系的函数。
通过引入新的变量来替代原来的变量,可以简化函数的形式,从而更容易计算极限。
七、分子有理化分子有理化是一种常用的极限计算方法,它适用于那些含有根式的函数。
通过将根式的分子有理化,可以将原函数转化为一个分式,从而更容易计算极限。
八、分部积分法分部积分法是一种常用的极限计算方法,它适用于那些含有积分的函数。
通过将原函数进行分部积分,可以将原函数转化为一个更简单的函数,从而更容易计算极限。
九、换元积分法换元积分法是一种常用的极限计算方法,它适用于那些含有复杂变量关系的函数。
通过引入新的变量来替代原来的变量,可以简化函数的形式,从而更容易计算极限。
十、二重极限法二重极限法是一种常用的极限计算方法,它适用于那些含有多个变量的函数。
高等数学中几种求极限的方法

高等数学中几种求极限的方法一、直接代入法这种方法超级简单,就是当函数在某一点连续的时候,直接把那个点的值代入函数里就好啦。
比如说啊,对于函数f(x)=x+1,当我们求x趋近于1的极限的时候,直接把1代入函数,就得到极限是2啦。
就像你走在路上,看到一个敞开的门,直接就可以走进去一样轻松。
二、因式分解法有时候函数看起来很复杂,但是我们可以对它进行因式分解呢。
比如说求lim(x→1)(x² - 1)/(x - 1),这个时候我们可以把分子因式分解成(x + 1)(x - 1),然后和分母的(x - 1)约掉,就变成了求lim(x→1)(x + 1),再用直接代入法就得到极限是2啦。
这就好比整理杂乱的房间,把东西整理好了,就很容易找到我们想要的啦。
三、有理化法当函数里有根式的时候,这个方法就很有用啦。
例如求lim(x→0)(√(1 + x)- 1)/x,我们可以把分子有理化,分子分母同时乘以(√(1 + x)+ 1),这样分子就变成了1 + x - 1 = x,然后和分母的x约掉,就得到极限是1/2啦。
这就像是给一个不太好看的东西化个妆,让它变得好看又好处理。
四、两个重要极限法1. 第一个重要极限是lim(x→0)sinx/x = 1。
这个极限超级重要哦。
比如说求lim(x→0)sin3x/x,我们可以把它变成3lim(x→0)sin3x/3x,根据第一个重要极限,就得到极限是3啦。
2. 第二个重要极限是lim(x→∞)(1 + 1/x)^x = e。
要是遇到类似lim(x→∞)(1+ 2/x)^x这种的,我们可以把它变形为lim(x→∞)[(1 + 2/x)^(x/2)]²,就等于e²啦。
这两个重要极限就像是数学世界里的宝藏,掌握了就能解决好多问题呢。
五、等价无穷小替换法当x趋近于0的时候,有好多等价无穷小的关系。
比如sinx和x是等价无穷小,tanx和x也是等价无穷小,ln(1 + x)和x也是等价无穷小等等。
高数中求极限的16种方法

千里之行,始于足下。
高数中求极限的16种方法在高等数学中,求极限是一个格外重要的技巧和考点。
为了解决各种极限问题,数学家们总结出了很多方法和技巧。
以下是高数中求极限的16种方法:1.代换法:将极限中的变量进行代换,使其变成简洁计算的形式。
2.夹逼准则:当函数处于两个已知函数之间时,可以通过比较已知函数的极限来确定未知函数的极限。
3.无穷小量比较法:比较两个函数的无穷小量的大小,以确定它们的极限。
4.利用函数性质:利用函数的对称性、奇偶性等性质来计算极限。
5.利用恒等变形:将极限式子进行恒等变形,以将其转化为简洁计算的形式。
6.利用泰勒开放:将函数开放成无穷级数的形式,以求出极限。
7.利用洛必达法则:对于某些不定型的极限,可以利用洛必达法则将其转化为可计算的形式。
8.利用级数或累次求和:将极限式子转化为级数或累次求和的形式,以求出极限。
9.利用积分计算:将极限式子进行积分计算,以求出极限。
10.利用微分方程:将极限问题转化为求解微分方程的问题,以求出极限。
第1页/共2页锲而不舍,金石可镂。
11.利用积素等价:将极限式子进行积素等价,以求出极限。
12.利用无穷增减变异法:通过凑出一个等价变形,将极限问题转化为比较某些函数值的大小。
13.利用不等式:通过找到合适的不等式,对函数进行估量,以求得极限。
14.利用递推公式:对于递归定义的函数,可以通过递推公式求出极限。
15.利用导数性质:利用函数的导数性质,对极限进行计算。
16.利用对数和指数函数的性质:利用对数和指数函数的特性,求出极限。
除了上述方法外,还有很多其他的方法和技巧,可以依据具体问题来选择使用。
这些方法和技巧的使用需要机敏把握,通过大量的练习和思考,可以在求解极限问题中得到娴熟应用。
Matlab求解方程和函数极值

Matlab求解方程和函数极值一.线性方程组求解1.直接解法①利用左除运算符的直接解法对于线性方程组Ax=b,可以利用左除运算符“\”求解:x=A\b例用直接解法求解下列线性方程组。
命令如下:A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b②利用矩阵的分解求解线性方程组矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积。
常见的矩阵分解有LU分解、QR分解、Cholesky分解,以及Schur分解、Hessenberg分解、奇异分解等。
(1) LU分解矩阵的LU分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积形式。
线性代数中已经证明,只要方阵A是非奇异的,LU分解总是可以进行的。
MATLAB提供的lu函数用于对矩阵进行LU分解,其调用格式为:[L,U]=lu(X):产生一个上三角阵U和一个变换形式的下三角阵L(行交换),使之满足X=LU。
注意,这里的矩阵X必须是方阵。
[L,U,P]=lu(X):产生一个上三角阵U和一个下三角阵L以及一个置换矩阵P,使之满足PX=LU。
当然矩阵X同样必须是方阵。
实现LU分解后,线性方程组Ax=b的解x=U\(L\b)或x=U\(L\Pb),这样可以大大提高运算速度。
例用LU分解求解例7-1中的线性方程组。
命令如下:A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';[L,U]=lu(A);x=U\(L\b)或采用LU分解的第2种格式,命令如下:[L,U ,P]=lu(A);x=U\(L\P*b)(2) QR分解对矩阵X进行QR分解,就是把X分解为一个正交矩阵Q和一个上三角矩阵R的乘积形式。
QR分解只能对方阵进行。
MATLAB的函数qr可用于对矩阵进行QR分解,其调用格式为:[Q,R]=qr(X):产生一个一个正交矩阵Q和一个上三角矩阵R,使之满足X=QR。
matlab实验二__极限与导数

实验二 极限与导数【实验目的】1.了解函数极限、导数的基本概念。
2.学习、掌握MATLAB 软件有关求曲线、导数的命令。
【实验内容】1.判断极限0011lim cos ,limsin x x x x →→的存在性。
2.验证极限0sin lim1x xx→=。
3.验证极限11lim(1)lim(1) 2.71828n x n x e n x →∞→∞+=+== 。
4.求函数363y x x =-+的单调区间及极值。
【实验准备】1.极限导数的基本概念2.求极限、导数的MATLAB 命令MATLAB 主要用limit,diff 分别求函数的极限与导数。
建立符号变量命令sym 和syms 调用格式: x=sym('x'), 建立符号变量x ;syms x y z , 建立多个符号变量x ,y ,z ; matlab 求导命令diff 调用格式: diff(函数) , 求的一阶导数;diff(函数, n) , 求的n 阶导数(n 是具体整数);diff(函数,变量名), 求对的偏导数;diff(函数, 变量名,n) ,求对的n 阶偏导数;matlab 求雅可比矩阵命令jacobian ,调用格式: jacobian([函数;函数; 函数], [])给出矩阵:【实验重点】1.极限的计算2.导数的计算 【实验难点】1.导数的曲线表示 【实验方法与步骤】 一、观察与练习练习1 首先分别作出函数1cos y x=在区间[1,0.01],[0.01,1],--[1,0.001],[0.001,1]--等区间上的图形,观察图形在0x =附近的形状。
在区间[1,0.01]--绘图的MATLAB 代码为>>x=(-1):0.0001:(-0.01); y=cos(1./x);plot(x,y) 运行结果如图2.1。
图2.1根据图形能否判断极限0011lim cos ,limsin x x xx→→的存在性? 当然,也可以用limit 命令直接求极限,相应的MATLAB 命令为 >>clear;>>syms x; %说明x 为符号变量 >>limit(sin(1/x),x,0)结果为ans=1 ..1,即极限值在-1,1之间,而如果极限存在则必唯一,故极限01lim sin x x→不存在。
高数中求极限的16种方法

高数中求极限的16种方法高数中求极限的16种方法——好东西首先对极限的总结如下:极限的保号性很重要,就是说在一定区间内,函数的正负与极限一致一、极限分为一般极限,还有数列极限,(区别在于数列极限发散,是一般极限的一种)二、求极限的方法如下:1 .等价无穷小的转化,(一般只能在乘除时候使用,在加减时候用必须证明拆分后极限依然存在)e的X次方-1 或者(1+x)的a次方-1等价于Ax 等等。
全部熟记(x趋近无穷的时候还原成无穷小)2.罗比达法则(大题目有时候会有暗示,要你使用这个方法)首先他的使用有严格的使用前提,必须是X趋近而不是N趋近!所以面对数列极限时候先要转化成求x趋近情况下的极限,当然n趋近是x趋近的一种情况而已,是必要条件还有一点数列极限的n当然是趋近于正无穷的不可能是负无穷!必须是函数的导数要存在!必须是0比0 无穷大比无穷大!当然还要注意分母不能为0注意:罗比达法则分为3种情况0比0,无穷比无穷的时候直接用;0乘以无穷,无穷减去无穷(应为无穷大于无穷小成倒数的关系)所以无穷大都写成了无穷小的倒数形式了。
通项之后这样就能变成1中的形式了;0的0次方,1的无穷次方,无穷的0次方;对于(指数幂数)方程,方法主要是取指数还取对数的方法,这样就能把幂上的函数移下来了,就是写成0与无穷的形式了,(这就是为什么只有3种形式的原因, LNx两端都趋近于无穷时候他的幂移下来趋近于0 当他的幂移下来趋近于无穷的时候LNX 趋近于0)3.泰勒公式(含有e的x次方的时候,尤其是含有正余弦的加减的时候要特别注意)E的x展开,sina 展开,cos 展开,ln1+x展开,对题目简化有很好帮助4.面对无穷大比上无穷大形式的解决办法取大头原则,最大项除分子分母5.无穷小于有界函数的处理办法面对复杂函数时候,尤其是正余旋的复杂函数与其他函数相乘的时候,一定要注意这个方法。
面对非常复杂的函数可能只需要知道它的范围结果就出来了6.夹逼定理(主要对付数列极限!)这个主要是看见极限中的函数是方程相除的形式,放缩和扩大。
matlab计算函数极值,如何用MATLAB求函数的极值点和最大值

matlab计算函数极值,如何⽤MATLAB求函数的极值点和最⼤值两种⽅法:1、求导的⽅法:syms x y;>>y=x^3+x^2+1>>diff(y)ans =3*x^2 + 2*x>>solve(ans)ans=-2/3极值有两点。
同时也是最值;2、直接⽤最⼩值函数:求最⼤值,既求-y的最⼩值:>>f=@(x)(-x^3-x^2-1)f =@(x)(-x^3-x^2-1)>>x=fminunc(f,-3,3)%在-3;-3范围内找Warning: Gradient must be provided fortrust-region method; using line-search methodinstead. > In fminunc at354Optimization terminated: relative infinity-norm of gradient lessthan options.TolFun.x =-0.6667>> f(x)ans =-1.1481在规定范围内的最⼤值是1.1481由于函数的局限性,求出的极值可能是局部最⼩(⼤)值。
求全局最值要⽤遗传算法。
例⼦:syms xf=(200+5*x)*(0.65-x*0.01)-x*0.45;s=diff(f);%⼀阶导数s2=diff(f,2);%⼆阶导数h=double(solve(s));%⼀阶导数为零的点可能就是极值点,注意是可能,详情请见⾼数课本fori=1:length(h)ifsubs(s2,x,h(i))<0disp(['函数在' num2str(h(i))'处取得极⼤值,极⼤值为' num2str(subs(f,x,h(i)))])elseifsubs(s2,x,h(i))>0disp(['函数在' num2str(h(i))'处取得极⼩值,极⼩值为'num2str(subs(f,x,h(i)))])elsedisp(['函数在' num2str(h(i))'处⼆阶导数也为0,故在该点处函数可能有极⼤值、极⼩值或⽆极值'])%%%详情见⾼数课本endend。
实验三 用matlab求极限和导数
实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。
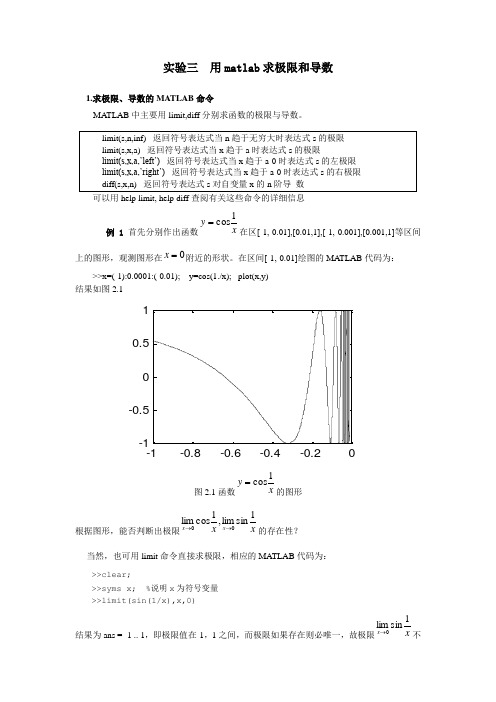
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形,能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sinlim 0→不存在,同样,极限x x 1coslim 0→也不存在。
例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形,能否判断出极限1sin lim0=→x xx 的正确性?当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学中极限的几种求法分析及Matlab仿真摘要:熟练和准确的进行极限计算是掌握高等数学以进行实际应用的基本要求,本文对极限的求解方法做了较为详细的归纳和总结,并针对这些方法进行了针对性的举例分析,并且每一个示例都通过Matlab软件进行了仿真,以验证各种方法的有效性。
关键词:函数极限计算方法Matlab
极限概念贯穿于高等数学始终,是建立连续、导数、积分、无穷级数等其他概念的重要基础,是正确理解微分与积分的前提。
本文在掌握极限的定义和极限运算法则的基础上,系统分析不同类型极限问题的计算方法,并针对具体问题给出了Matlab源代码加以验证。
1 运用极限存在准则
该文所介绍的方法在很多情况下是需要把其中两种或多种方法灵活地结合起来使用,才能有效地解决不同类型的极限问题。
而且这里列举的方法并不是求解极限的全部方法,如运用单调有界定理、黎
曼引理求极限等方法在本文并未介绍。
求解极限的过程就是综合运用各种方法的过程,唯有真正掌握数学的思维方法,才能在求解极限的过程中游刃有余。
随着知识的不断进步,相信会有更多更好的方法求解极限问题。
参考文献
[1] 李鸿鹏.浅谈求极限的几种计算方法[J].科技创新导报,2008(21).
[2] 胡适耕.大学数学解题艺术[M].湖南大学出版社,2002.
[3] 黄美初.函数极限计算的几种重要方法[J].南京广播电视大学学报,2003(2).
[4] 林新和.高等数学中求极限几种常见方法[J].呼伦贝尔学院学报,2005(6).。
