【八下数学】人教版八年级数学下册19.1函数的概念 (1)ppt课件—精选资料
合集下载
八年级数学19.1《函数》(共70张PPt)

的值为a时的函数值。
【例题】
【例】一辆汽车的油箱中现有汽油50L,如果不再加油,那 么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增 加而减少,平均耗油量为0.1L/km. (1)写出表示y与x的函数关系的式子. (2)指出自变量x的取值范围. (3)汽车行驶200km时,油箱中还有多少汽油? 【解析】(1)行驶里程x是自变量,油箱中的油量y是x的 函数,它们的关系为 y=50-0.1x.像y=50-0.1x这样,用关 于自变量的数学式子表示函数与自变量之间的关系,是描 述函数的常用方法,这种式子叫做函数的解析式.
【备选例题】(2017·内江中考)在函数y= x 3 中, x4 自变量x的取值范围是 ( )
A.x>3
C.x>4
B.x≥3
D.x≥3且x≠4
【解析】选D.∵x-3≥0,∴x≥3,∵x-4≠0,∴x≠4, 综上,x≥3且x≠4.
【微点拨】 确定自变量取值范围的方法
(1)函数解析式是整式,自变量的取值范围是任意实数.
【观察发现】
共同特征:
1.都有两个变量.
2.其中的一个变量取定一个值,另一个变量的值也唯一 确定. 我们称另一个变量是这个变量的函数.
例如:对于函数y = 2 x ,取定x=3,y有唯一的
值6与x=3对应,此时我们把6叫做当自变量的做当自变量
【自主解答】(1)表中反映了弹簧长度与所挂砝码质量 之间的关系;其中所挂砝码质量是自变量,弹簧长度是
所挂砝码质量的函数.
(2)弹簧的原长是18cm;当所挂砝码质量为3g时,弹簧长 24cm.
(3)根据表中数据可知,砝码质量每增加1g,弹簧的长度
增加2cm. 【互动探究】你能知道在弹性限度内,x=10g时,弹簧的 长度吗? 提示:当x=10时,y=18+2×10=38,故当x=10g时,弹簧的 长度为38cm.
人教版八年级数学下册《函数》PPT课件

问题二 电影票的售价为 10 元/张 ,第一场售出150 张, 第二场售出 205 张,第三场售出 310 张,三场电影票的 票房收入各多少元?设一场电影售出票 x 张,票房收入
为 y 元,每场的票房收入是多少呢 ? y = 10x
这个问题中有几个变量? 两个
当 x 取定一个值时,y 有几个值与之对应? 一个
பைடு நூலகம்
问题三 在圆的面积 S 和半径 r 中,r 每取一个值,
S 都有唯一值与它对应吗?
S = πr2
根据圆的面积计算公式 S = πr2,由 于 π 为常量,所以 r 每取一个值,S 都 有唯一值与它对应.
同理 问题四 中边长 x 每取一个值,邻边长 y 都有唯 一值与它对应.
思考:上面的三个问题中,各变量之间有什么共同
例2 已知函数 y 4x 2 .
x 1
(1) 求当 x = 2 ,3,-3 时,函数的值;
(2) 求当 x 取什么值时,函数的值为 0.
解:(1) 当 x = 2 时,y = 4 2-2 =2;
2+1
当 x = 3 时,y = 5 ;
2
当 x = -3 时,y = 7.
把自变量 x 的值带 入关系式中,即可
(3) 汽车行驶 200 km 时,油箱中还有多少油?
(3) 当 x = 200 时,函数 y 的值为 y = 50-0.1×200 = 30.
因此,当汽车行驶 200 km 时,油箱中还有油 30 L.
函数
一般地,在某个变化过程中,如果 有两个变量 x 与 y,并且对于 x _每__一__个__确__定__的值,y 都有_唯__一__确__定__ 的值与它对应,那么我们就说 x 是 _自__变__量__,y 是 x 的_函__数____.
人教版八年级下册19.1.1函数1课件23张ppt

行驶的路程s随着 时间t的变化而变化.
自主学习
(2)电影票售价为10元/张,第一场售出150张票,第二 场售出205张票,第三场售出310张票,三场电影的票房收 入各多少元?设一场电影售出x张票,票房收入y元.
x/张 150 205 310 x
y/元
在这个变化的过程中, 每张电影的售价(10元)是固定不变 的,电影的售票数和票房的收入(x,y)是不断变化的。
(4)汽油的价格是7.4元/升,加油 x L并写出它们的 关系式:
(5)从甲市到乙市的寄包裹的邮费为0.9元/千克, 每件另加手续费3元,包裹重x(千克),总邮费y(元).
指出下列变化过程中的变量和常量,并写出它们 的关系式:
(6)用长为40 cm 的绳子围矩形,围成的矩形一边 长为 x cm,其面积为 S cm2.
拓展延伸
如下图△ABC 底边BC上的高是6cm,当三角形的顶点B 沿 面底 积边发生BC了向变点化C.运动时(点B与点C不重合),A 三角形的
(1)如果三角形的底边BC的长为 x cm , 那么三角形的面积为 y cm2,用含x的式 子表示y,并指出其中的常量和变量;
B C1C 2C 3 C 4 C 5 C (2)当BC的长从3cm变化到12cm 时,三角形的面积
2.常量除了用常数表示也可以用字母表示.
人有胖瘦之分,体重过轻则为瘦,过重则为胖,那么 以什么样的标准来衡量是胖还是瘦呢?这当然必须有个 参照值.这个参照值我们就把它称之为标准体重,标准 体重G和身高h之间的关系:
G男 =h男-105
G女 =h女-100
这里什么是常量?什么是变量?
据科学研究,10岁至50岁的人每天最低所需睡 眠时间H(时)可用公式 H=(110-N)÷10(N是人 的年龄)来计算,请说出其中的常量和变量.
自主学习
(2)电影票售价为10元/张,第一场售出150张票,第二 场售出205张票,第三场售出310张票,三场电影的票房收 入各多少元?设一场电影售出x张票,票房收入y元.
x/张 150 205 310 x
y/元
在这个变化的过程中, 每张电影的售价(10元)是固定不变 的,电影的售票数和票房的收入(x,y)是不断变化的。
(4)汽油的价格是7.4元/升,加油 x L并写出它们的 关系式:
(5)从甲市到乙市的寄包裹的邮费为0.9元/千克, 每件另加手续费3元,包裹重x(千克),总邮费y(元).
指出下列变化过程中的变量和常量,并写出它们 的关系式:
(6)用长为40 cm 的绳子围矩形,围成的矩形一边 长为 x cm,其面积为 S cm2.
拓展延伸
如下图△ABC 底边BC上的高是6cm,当三角形的顶点B 沿 面底 积边发生BC了向变点化C.运动时(点B与点C不重合),A 三角形的
(1)如果三角形的底边BC的长为 x cm , 那么三角形的面积为 y cm2,用含x的式 子表示y,并指出其中的常量和变量;
B C1C 2C 3 C 4 C 5 C (2)当BC的长从3cm变化到12cm 时,三角形的面积
2.常量除了用常数表示也可以用字母表示.
人有胖瘦之分,体重过轻则为瘦,过重则为胖,那么 以什么样的标准来衡量是胖还是瘦呢?这当然必须有个 参照值.这个参照值我们就把它称之为标准体重,标准 体重G和身高h之间的关系:
G男 =h男-105
G女 =h女-100
这里什么是常量?什么是变量?
据科学研究,10岁至50岁的人每天最低所需睡 眠时间H(时)可用公式 H=(110-N)÷10(N是人 的年龄)来计算,请说出其中的常量和变量.
义务教育人教版数学八年级下册《函数》PPT课件

一确定的值与其对应;(3)中,y不是x的函数,因为对于x的每一个
确定的值,y都有两个确定的值与其对应.将关系式改为 y x 2
或 y x 2 ,都能使y是x的函数.
问题3:变量x与y的对应关系如下表所示:
x 1 4 9 16 25 … y ±1 ±2 ±3 ±4 ±5 …
问:变量y是x的函数吗?为什么?若要使y是x的 函数,可以怎样改动表格?
(1)这天的8时的气温是 (2)这一天中,最高气温 是 10 ℃,最低气温是 -2 ℃;
图一
与函数有关的概念
一般地,在一个变化过程中, 如果有两个变量x和y,并且 对于x的每一个确定的值,y 都有唯一确定的值与其对应 , 那么我们就说x是自变 量,y是 x的函数.如果当x=a时y=b,那 么b叫做当自变量的值为a时 的函数值
练一练
1.购买一些签字笔,单价3元,总价为y元,签字笔为x支,根 据题意填表:
x
1
2
y
3
6
3…
9
(1) y随 x变化的关系式
, 是自变量, 是 的函数;
(2)当购买8支签字笔时,总价为 元.
练一练
2.周末,小李8时骑自行车从家里出发,到野外郊游,16时
回到家里.他离开家后的距离 (千米)与时间 (时)的关
y
-1,1 5,-5 -8,8 无
y是x的函数吗?为什么?
难点质疑
问题1:下列式子中的y是x的函数吗?为什么?若
y不是x的函数,怎样改变,才能使y是x的函数?
(1) y 2x 3
(2) y 1 x 1
(3) y x 2
(1)、(2)中y是x的函数,因为对于x的每一个确定的值,y都有唯
则y= 10x
人教版八年级数学下册课件:19.1函数--1.2 函数的图象(1)认识函数的图象(共38张PPT)
15
知识点二:由图象读取信息
典例讲评
例2 如图1所示,小明家、 食堂、图书馆在同一条直线
上.小明从家去食堂吃早餐,接着去图书馆读报, 然后 回家.图2反映了这个过程中,小明离家的距离y与时间x 之间的 对应关系.
16
知识点二:由图象读取信息
典例讲评
根据图象回答下列问题: (1)食堂离小明家多远?小明从家到食 堂用了多少时间? (2)小明吃早餐用了多少时间?
新知探究
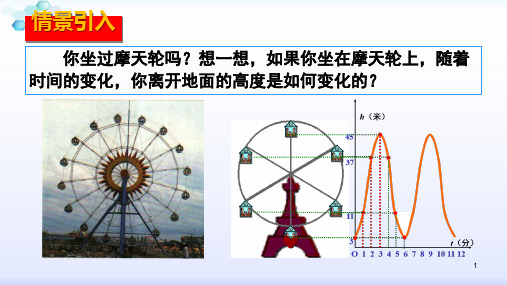
下图是自动测温仪记录的图象,它反映了北 京的春季某天气温T如何随时间 t 的变化而变化.你从图 象中得到了哪些信息?
14
知识点二:由图象读取信息
新知探究
由图象可知: (1)这一天中凌晨4时气温最低(-3 ℃),14时气温最高(8 ℃). (2)从0时至4时气温呈下降状态(即温度随时间的增长而下降), 从4 时到14时气温呈上升状态,从14时至24时气温又呈下降 状态. (3)我们可以从图象中看出这一天中任一时刻的气温大约是 多少.
7
知识点一:函数的图象
合作探究
先独立完成导学案互动探究2,再同桌相互交流, 最后小组交流;
8
知识点一:函数的图象
学以致用
1.向高为H的水瓶中注水,注满为止,如果注水量V与水深h 的函数关系的图象如图所示,那么水瓶的形状是( A )
9
知识点一:函数的图象
学以致用
2.已知点A(-1,1),B(1,1),C(2,4)在同一个函数的图象 上,这个函数图象可能是( B )
18
知识点二:由图象读取信息
典例讲评
根据图象回答下列问题: (4)小明读报用了多少时间? (5)图书馆离小明家多远?小明从图书 馆回家的平均速度是多少?
(4)由横坐标看出,58-28=30,小明读报用了 30 min. (5)由纵坐标看出,图书馆离小明家0.8 km;由 横坐标看出,68-58=10,小明从图书馆回 家用了 10 min,由此算出平均速度是0.08 km/min.
知识点二:由图象读取信息
典例讲评
例2 如图1所示,小明家、 食堂、图书馆在同一条直线
上.小明从家去食堂吃早餐,接着去图书馆读报, 然后 回家.图2反映了这个过程中,小明离家的距离y与时间x 之间的 对应关系.
16
知识点二:由图象读取信息
典例讲评
根据图象回答下列问题: (1)食堂离小明家多远?小明从家到食 堂用了多少时间? (2)小明吃早餐用了多少时间?
新知探究
下图是自动测温仪记录的图象,它反映了北 京的春季某天气温T如何随时间 t 的变化而变化.你从图 象中得到了哪些信息?
14
知识点二:由图象读取信息
新知探究
由图象可知: (1)这一天中凌晨4时气温最低(-3 ℃),14时气温最高(8 ℃). (2)从0时至4时气温呈下降状态(即温度随时间的增长而下降), 从4 时到14时气温呈上升状态,从14时至24时气温又呈下降 状态. (3)我们可以从图象中看出这一天中任一时刻的气温大约是 多少.
7
知识点一:函数的图象
合作探究
先独立完成导学案互动探究2,再同桌相互交流, 最后小组交流;
8
知识点一:函数的图象
学以致用
1.向高为H的水瓶中注水,注满为止,如果注水量V与水深h 的函数关系的图象如图所示,那么水瓶的形状是( A )
9
知识点一:函数的图象
学以致用
2.已知点A(-1,1),B(1,1),C(2,4)在同一个函数的图象 上,这个函数图象可能是( B )
18
知识点二:由图象读取信息
典例讲评
根据图象回答下列问题: (4)小明读报用了多少时间? (5)图书馆离小明家多远?小明从图书 馆回家的平均速度是多少?
(4)由横坐标看出,58-28=30,小明读报用了 30 min. (5)由纵坐标看出,图书馆离小明家0.8 km;由 横坐标看出,68-58=10,小明从图书馆回 家用了 10 min,由此算出平均速度是0.08 km/min.
数学 八年级下册人教版 第十九章 一次函数 19 1 1 函数的定义 课件

• 学习重点: 概括并理解函数概念中的单值对应关系.
什么是常量?什么是变量?
温馨提示:师友典型发言时学友先回答;师傅再补充,对师友存在 的共性问题进行重点强调
问题1 下面变化过程中的变量之间有什么联系? (1)汽车以60 km/h 的速度匀速行驶,行驶的时间 为t h,行驶的路程为s km; 行驶时间 t/h 1 3 3.4 4 9 … 行驶里程s/km 60 180 204 240 540 …
巩固性作业: 必做:1. 2. 选做:
预习性作业:
如果当 x =a 时,对应的 y =b, 那么 b 叫做当自变量的值为 a 时的函数值.
谈谈你对函数有什么认识?
练习1 下列问题中,一个变量是否是另一个变量的 函数?请说明理由.
(1)向一水池每分钟注水0.1 m3,注水量 y(单位: m3)随注水时间 x(单位:min)的变化而变化;
(2)改变正方形的边长 x,正方形的面积 S 随之变化; (3)秀水村的耕地面积是106 m2,这个村人均占有耕 地面积 y (单位:m2)随这个村人数 n 的变化而变化; (4)P是数轴上的一个动点,它到原点的距离记为 x,
届数 x/届 23 24 25 26 27 28 29 30
金牌数 y/枚
15
5
16
16
28 32
51
38
问题4 如图是北京某天的气温变化图,你能根据 图象说出某一时刻的气温吗?
综合以上这些现象,你能再次归纳出上面所有事例 的变量之间关系的共同特点吗?
一一对应
函数的定义: 一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
什么是常量?什么是变量?
温馨提示:师友典型发言时学友先回答;师傅再补充,对师友存在 的共性问题进行重点强调
问题1 下面变化过程中的变量之间有什么联系? (1)汽车以60 km/h 的速度匀速行驶,行驶的时间 为t h,行驶的路程为s km; 行驶时间 t/h 1 3 3.4 4 9 … 行驶里程s/km 60 180 204 240 540 …
巩固性作业: 必做:1. 2. 选做:
预习性作业:
如果当 x =a 时,对应的 y =b, 那么 b 叫做当自变量的值为 a 时的函数值.
谈谈你对函数有什么认识?
练习1 下列问题中,一个变量是否是另一个变量的 函数?请说明理由.
(1)向一水池每分钟注水0.1 m3,注水量 y(单位: m3)随注水时间 x(单位:min)的变化而变化;
(2)改变正方形的边长 x,正方形的面积 S 随之变化; (3)秀水村的耕地面积是106 m2,这个村人均占有耕 地面积 y (单位:m2)随这个村人数 n 的变化而变化; (4)P是数轴上的一个动点,它到原点的距离记为 x,
届数 x/届 23 24 25 26 27 28 29 30
金牌数 y/枚
15
5
16
16
28 32
51
38
问题4 如图是北京某天的气温变化图,你能根据 图象说出某一时刻的气温吗?
综合以上这些现象,你能再次归纳出上面所有事例 的变量之间关系的共同特点吗?
一一对应
函数的定义: 一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
19.1.1 变量与函数 课件(共16张PPT) 人教版初中数学八年级下册
(2)用关系式表示你猜想的变化规律,并指出关系式中的常量. 变化规律满足:y=280-x,关系式中的常量是:数字280.
当堂检测
指出下列问题中的变量和常量: (1)购买一些铅笔,单价为0.2元/支,记某同学购买铅笔 的数量为x支,应付的总价为y元;关系式为 y=0.2x 。 其中的变量是 x、y ,常量是 0.2 。
例3、根据销售记录,某型号的服装每天的售价x(元/件 )与当日的销售量y(件)的变化关系如下表:
每天的销售价 x(元/件) 200 190 180 170 160 150 140 …
每天的销售量 y(件) 80 90 100 110 120 130 140 …
(1)在这个变化过程中,有哪些变量?是哪一个量随 哪一个量的变化而变化?并指出其中的常量. 变量有:服装每天的售价x(元/件)和当日的销售量y(件), 当日的销售量y随服装每天的售价x的变化而变化.
t/h s/km
1 2345 60 120 180 240 300
在这个变化的过程中,行驶的 速度 60km/h 是固
定不变的,行驶的 路程s和时间t
是不断变化的.
路程s 着 时间t 的变化而变化.
试用含t的式子表示s 是__s_=6_0_t____
探究 (2)电影票售价为10元/张,第一场售出150张票,第二场售出205 张票,第三场售出310张票,三场电影的票房收入各多少元?设一场 电影售出x张票,票房收入y元. y的值随x的值的变化而变化吗?
x
a
图1
图2
瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数 y与层数x之间的关系式.
x1 2 3 …
x
y 1 1+2 1+2+3 … 1+2+3+ …+x
当堂检测
指出下列问题中的变量和常量: (1)购买一些铅笔,单价为0.2元/支,记某同学购买铅笔 的数量为x支,应付的总价为y元;关系式为 y=0.2x 。 其中的变量是 x、y ,常量是 0.2 。
例3、根据销售记录,某型号的服装每天的售价x(元/件 )与当日的销售量y(件)的变化关系如下表:
每天的销售价 x(元/件) 200 190 180 170 160 150 140 …
每天的销售量 y(件) 80 90 100 110 120 130 140 …
(1)在这个变化过程中,有哪些变量?是哪一个量随 哪一个量的变化而变化?并指出其中的常量. 变量有:服装每天的售价x(元/件)和当日的销售量y(件), 当日的销售量y随服装每天的售价x的变化而变化.
t/h s/km
1 2345 60 120 180 240 300
在这个变化的过程中,行驶的 速度 60km/h 是固
定不变的,行驶的 路程s和时间t
是不断变化的.
路程s 着 时间t 的变化而变化.
试用含t的式子表示s 是__s_=6_0_t____
探究 (2)电影票售价为10元/张,第一场售出150张票,第二场售出205 张票,第三场售出310张票,三场电影的票房收入各多少元?设一场 电影售出x张票,票房收入y元. y的值随x的值的变化而变化吗?
x
a
图1
图2
瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数 y与层数x之间的关系式.
x1 2 3 …
x
y 1 1+2 1+2+3 … 1+2+3+ …+x
人教版八年级下册数学第十九章《 19.1变量与函数》优课件(共28张PPT)

在问题三中,是否各有两个变量?同一 个问题中的变量之 间有什么联系?
问题三
在一根弹簧的下端挂重物,改变并记录重物的质量, 观察并记录弹簧长度的变化,探索它们的变化规律。如 果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?
八年级 数学
第十九章 一次函数
19.1.1变量与函数
解:∵花盆图案形如三角形,每边花有n个,总共有3n个, 其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3
八年级 数学
第十九章 一次函数
19.1.1变量与函数 课堂练习(备用)
4、节约资源是当前最热门的话题,我市居民每月用电 不超过100度时,按0.57元/度计算;超过100度电时,其中不 超过100度部分按0.57元/度计算,超过部分按0.8元/度计算.
常量:在一个变化过程中,数值始终不变的量为常量。
请指出上面各个变化过程中的常量、变量。
八年级 数学
第十九章 一次函数
19.1 .1 变量与函数
探究:指出下列关系式中的变量与常量:
(1) y = 5x -6
6
(2) y= x
(3) y= 4x2+5x-7 (4) S = Лr2
巩固练习
• 填空:
• 1、计划购买50元的乒乓球,所能购买的总数
2.圆的周长公式C2r,这里的变量是 r和C ,常量
是 2 。
3.下列表格是王辉从4岁到10岁的体重情况
年龄(岁) 4 5 6 7 8 9
10 …
体重(千克)15.4 16.7 18.0 19.6 21.5 23.2 25.2 …
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温度T (℃)
8
6
4
2
时间t
0
(时)
2
4
6
8
10
12
14
16
18
20
22
24
-2
探索新知
例题2 下列变化过程中,两个变量之间是否存在确定的依赖关系?其中一个变量 是另一个变量的函数吗?
(2)近年来上海市区的环境绿化不断得到改善,下表是上海市区人均绿化面积变化的 一些统计数据:
年份 人均绿化面积(㎡)
质量 地心最高温度
598×1019吨 5000 ℃
自转一周所需的时间 23时56分4.1秒
绕太阳运行的平均速度 29.77千米/秒
这里所涉及的量,有长度,面积,体积,质量,温度,时 间,速度等。
探索新知
问题1、
地球上的赤道是一个大圆,半径长r0≈6.378×106 (米). 设想有一个飞行器环绕赤道飞行一周,其轨道是与赤道在同一平面且同圆 心的圆E.如果圆E的周长比赤道的周长多a米,那么圆E的半径长r是多少米?
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。 • 二、补笔记 • 上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一
r
r0பைடு நூலகம்
a
2
变量r与a之间存在 确定的依赖关系
在问题研究的过程中,可以取不同数值的量叫做变量 保持数值不变的量叫做常量(或常数)
探索新知
问题2 一辆汽车行驶在国道上,汽车油箱里原有汽油120升,每行驶10千米耗油2 升。
(1)填表
汽车行驶的路程
100km 150km
200km 250km
油箱里剩余的油量
5 例如下表:
摄氏度数x(℃)
… -10 0
25 35 100 …
华氏度数y(℉)
…
…
可见,变量y与x之间存在确定的依赖关系,y是x的函数, 是这个函数的解析y 式9。x 32
5
探索新知
例题2 下列变化过程中,两个变量之间是否存在确定的依赖关系?其中一个变量 是另一个变量的函数吗?
(1)某气象站测得当地某一天的气温变化情况如图所示:
巩固拓展
3、已知物体匀速运动中,路程s、速度v、时间t之间有关系式 s=vt.
(1)如果速度不变,那么这个式子里哪两个量是变量?这 两个变量中哪一个是自变量?哪一个是自变量的函数?如果 时间不变呢?
(2)如果路程不变,试写出速度关于时间的函数解析式.
编后语
• 常常可见到这样的同学,他们在下课前几分钟就开始看表、收拾课本文具,下课铃一响,就迫不及待地“逃离”教室。实际上,每节课刚下课时的几分 钟是我们对上课内容查漏补缺的好时机。善于学习的同学往往懂得抓好课后的“黄金两分钟”。那么,课后的“黄金时间”可以用来做什么呢?
(0≤x≤600)
探索新知
在某个变化过程中有两个变量,设x为和y,
如果在变量x的允许取值范围内,变量y随着x的变化而变
化,
它们之间存在确定的依赖关系
那么变量y叫做变量x的函数
x叫做自变量
在问题2中,变量y是变量x的函数,x是自变量,其中y随着 x变化而变化的依赖关系,是由“y=120-0.2x”表达出来的。
探索新知
议一议 如果x是一个变量,那么x+2也是一个
变量。 试问:变量x+2是不是变量x的函数?
巩固拓展
1、举出一个含有两个相关变量的实例,指出其中一个变量是否是另一 个变量的函数.如果是,请把它们的依赖关系表达出来.
2、某校学生总人数1200,某天实际到校的学生人数n与学 生的出勤率p是两个变量.试说明p是n的函数,并写出这个函数 解析式.
100升 90升 80升
70升
(2)在汽车行驶过程中,汽车行驶的路程和油箱里剩余的油量都是变 量吗?
(3)设汽车行驶的路程为x千米,油箱里剩余的油量为y升,那么y与x 之间是否存在确定的依赖关系?
答:汽车行驶的路程x(千米)和油箱里剩余的油量y(升)都是变量,y 随着x的变化而变化.
y=120-0.2x
2000
2001 2002 2003
2004
2005
4.5
5.5
7.0
9.4
10.0
11.0
答:两个变量是年份和人均绿化面积。 由表可知,随着所列年份的变化,上海市区人均绿化面积也在变化; 对于所列的每一个年份,在表格中都可以找到这一年人均绿化面积的数 值。 可见这两个变量之间也存在确定的依赖关系(通过列表来表达), 所以人均绿化面积是年份的函数
遍自己写的笔记,既可以起到复习的作用,又可以检查笔记中的遗漏和错误。遗漏之处要补全,错别字要纠正,过于潦草的字要写清楚。同时,将自己 对讲课内容的理解、自己的收获和感想,用自己的话写在笔记本的空白处。这样,可以使笔记变的更加完整、充实。 • 三、课后“静思2分钟”大有学问 • 我们还要注意课后的及时思考。利用课间休息时间,在心中快速把刚才上课时刚讲过的一些关键思路理一遍,把老师讲解的题目从题意到解答整个过 程详细审视一遍,这样,不仅可以加深知识的理解和记忆,还可以轻而易举地掌握一些关键的解题技巧。所以,2分钟的课后静思等于同一学科知识的 课后复习30分钟。
2019/7/7
最新中小学教学课件
thank
you!
2019/7/7
最新中小学教学课件
19.1(1)
函数的概念
回顾旧知
人们在认识和描述某一事物时,经常会用“量”来具体表达事物些特 征(属性),同时用“数”来表明量的大小。
数和度量单位合在一起,就是“数量”。
例如,我们居住的地球,可以用下列数量来描述它的一些特征:
平均半径
6371.22千米
表面积 体积
510×106平方千米 1083×109立方千米
这种表达两个变量之间依赖关系的数学式子称 为函数解析式。
探索新知
例题1 气温的摄氏度数x与华氏度数y之间可以进行如下转化,华氏度数y是不是 摄氏度数x的函数?为什么?
y 9 x 32 5
解:在把摄氏度转化为华氏度的过程中,华氏度y随着摄氏度x的变化而 变化;
由 y 9 x ,32当x取一个值时,y的值也随之确定,
