25个物理常数
常用化合物物理化学常数表
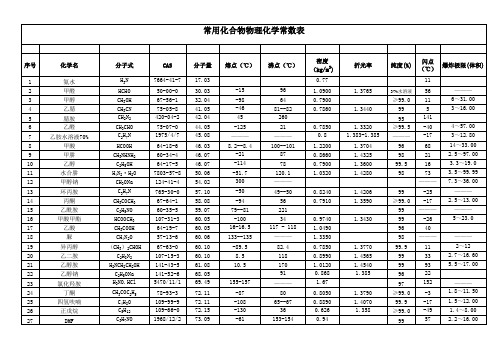
1.3765 1.3440 1.3320 1.383-1.385 1.3704 1.4325 1.3600 1.4280 1.4206 1.3590 1.3430
37%水溶液
≥99.0 99 95 ≥99.5 ——— 96 98 99.5 98 99 ≥99.0 99 99 96 98 1.3770 1.4565 1.4540 1.385 1.3790 1.4070 1.358 99.9 99 99 96 97 ≥99.0 99.9 ≥99.0 99
99 1.5280 0.6590 0.9370 1.41 1.0340 0.9020 0.7400 0.8090 2.92 1.17 0.8670 1.01 1.2610 0.8650 1.1830 0.8860 1.0220 1.3790 1.4442-1.4462 1.4740 1.4960 1.4380 1.4024 1.5860 1.3750 1.4380 1.4220 1.3720 1.3690 1.4060 99.99 95 ≥99.9 ≥99.0 ≥99.5 99 ≥99.0 99 98 ≥99.5 ≥99.0 ≥99.0 ≥99.5 99.5 ≥99.0 ≥99.0 ≥99.5
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93
4-甲基吡啶 苯酚 间氨基吡啶 2-甲基吡嗪 氟苯 1,2-二甲基咪唑 间氟吡啶 顺丁烯二酸酐 甲基环已烷 丁二酸酐 环丙基甲酸甲酯 正庚烷 二异丙胺 三乙胺 正戊酸 异丙醚 苯腈 二乙烯三胺 苯乙烯 一缩二乙二醇 苯甲醛 对二甲苯 乙基苯 间二甲苯 苄胺 邻甲苯胺 间甲苯胺 对甲苯胺 2,6-二甲基吡啶 对苯醌 苯甲醇 苯甲醚 间苯二胺
常用物理基本常数表

常用物理基本常数表
物理常数,或称物理定数、物理常量或自然常数,指的是物理学中数值固定不变的物理量。
它与数学常数不同,数学常数指的是一个在数值上固定不变的值,但是这个值不一定与物理测量有关。
物理常数有很多,其中比较著名的有真空光速、普朗克常数、万有引力常数、玻尔兹曼常数及阿伏伽德罗常数。
它们被假设在宇宙中任何地方和任何时刻都相同。
物理常数的物理意义有很多表述形式,普朗克长度表征基本物理长度,真空光速是宇宙中最大的速度,精细结构常数则表征了电子和光子之间的相互作用,是一个无量纲量。
从1937年开始,狄拉克等物理学家开始意识到物理常数有可能随着宇宙年龄的增长而发生变化,但时至今日还没有明确的实验证据能够证明狄拉克提出的这种可能性。
但科学家们已经探测到了一些物理量可能每年都依极小的量发生变化,并划定了这种变化幅度可能的上限(万有引力常数变化的量大约是一年10-11;精细结构常数变化的量大约是一年10-5)。
以下是部分物理常数的列表:。
基本物理常数

基本物理常数自然界四大基本力:强核力相对强度1,电磁力相对强度1/138,弱核力相对强度10^-6,引力相对强度6×10^-39。
1. 普朗克常数6.63×10^-34J·s,离散世界的基本物理量。
2. 普朗克时间5.39×10^-44s,最小的有意义的时间间隔。
3. 普朗克长度1.62×10^-35m,物理定律所适用范围内的最小尺度。
4. 普朗克密度5.2×10^96kg/m3,宇宙最早时刻的质量密度。
5. 宇宙的密度8.51×10^-27kg/m3,处于引力和膨胀力抗衡的临界点。
6. 电子的质量9.11×10^-31kg,带负电的亚原子粒子。
7. 质子的质量1.6726×10^-27kg,带正电的质子是元素周期表的缔造者。
8. 中子的质量1.6749×10^-27kg,离开原子后平均寿命只有15min。
9. 光子的静止质量0,光子与电磁力的载体玻色子没有任何质量。
10. 玻色子平均寿命3×10^-25s,自然界基本作用力的载体。
11. 银河中心黑洞的质量8×10^36kg,太阳绕其一圈需要2.2亿年。
12. 一个太阳质量的黑洞衰变时间2×10^67年,黑洞通过霍金辐射而蒸发。
13. 蓝色可见光波长4×10^-7m,天空散射的颜色。
14. 电子的波长8.7×10^-11m,以8.39×10^6m/s的速度产生的物质波。
15. 网球的波长7×10^-34m,重57g的网球以60km/h的速度产生的物质波。
16. 玻尔兹曼常数1.38×10^-23J/K,微观与宏观世界的桥梁。
17. 绝对零度-273.15℃,一切粒子的振动停止。
18. 铯原子振荡次数9192631770,定义1s的依据。
19. 真空中的光速299792458m/s,信息传递的极限。
28个物理学基本参数都是哪些?

28个物理学基本参数都是哪些?物理学中的基本参数并不止28个,通常所说的28个基本参数只是相对来说比较常用;如果进行粗略地分类的话,会有如下几种类型:第一类物理量:万有引力常数G这是牛顿万有引力定律中不可或缺的一个常数,基本上和天体相关的计算都会用到。
第二类物理量:光速,基本电荷,普朗克常数,波尔兹曼常数等。
这些物理量主要应用于微观领域,例如普朗克常数属于量子领域,而光速属于相对论领域,基本电荷属于电磁学领域。
第三类物理量:原子质量,阿伏伽德罗常数这些物理量则是应用于微观计数领域。
第四类物理量:基本物理量的衍生常数。
因为物理学中的实际参数非常多,因此不可能用这28个就能完全表示,因此根据实际需要,就会从这些基本量衍生出一些物理量;以上的介绍是对物理量的一些基本概括,下面则是这28个物理量的详细解释,如符号,名称,数值等。
名称符号数值单位(SI)万有引力常数 G 6.6720 x10^-11·Nm·kg^-2光速C 2.99792458 10^8m·s^-1统一原子质量单位 U 1.6605655 10^-27kg电子质量 me 9.109534 10^-31kg质子质量 mp 1.6726485 10^7kg中子质量 mn 1.6749543 10^-27kg基本电荷 e 1.6021892 10^-29C电子比荷e/me 1.7588 10^11C·kg^-1电子半径 re 2.8179 10^-15m普朗克常数 h 6.626176 10^-24J·s斯蒂芬·波尔兹曼常数σ 5.67032 10^-8w·m^-2·k^-4 玻尔半径 a0 137.036045 10^-3 ---- 10^-11里德伯常数 R 1.097373177 10^7 m^-1磁通量子 h/e 4.135701 10^-15J·s·c^-1玻尔磁子μB 9.274078 10^-24J·T^-1电子磁μe 9.284832 10^-24J·T^-1自由电子的g因子2μe/μB 2.00231931 --------核磁子μN 5.050824 10^-27J·T^-1质子的磁惯量μp 1.4106171 10^-26J·T^-1质子的磁角动量比γp 2.6751987 10^-15S·T^-1电子康普顿波长λe 2.4263089 10^-12m质子的康普顿波长λp 1.3214099 1 0^-15m中子的康普顿波长λca 1.3195909 10^-15m波尔兹曼常数 K 1.380662 10^-23·K^-1阿伏伽德罗常数Nλ 6.022045 10^23mol^-1完全气体的体积 V0 2.241383 10^-2m^-3·mol^-1摩尔气体常数R 8.31441 J·mol^-1·K^-1法拉第常数F 9.648456 10^4·mol以上就是你想要知道的28个基本物理参数,当然也有其他的参数,由于篇幅的原因就不列出所有的了。
初中物理基本物理量公式及常数

初中物理基本物理量公式及常数物理是研究非生物自然界的基本规律以及物质与能量之间相互关系的学科。
在物理学中,有许多基本物理量、公式和常数是我们必须熟悉和掌握的。
下面是一些常见的基本物理量、公式和常数的介绍。
一、基本物理量1.长度(L):用来计量物体的大小、距离等,国际单位是米(m)。
2. 质量(m):用来计量物体的惯性、重量等,国际单位是千克(kg)。
3.时间(t):用来计量事件发生的顺序、持续时间等,国际单位是秒(s)。
4.电流(I):用来计量电荷运动的强弱等,国际单位是安培(A)。
5.温度(T):用来计量物体的热量状态等,国际单位是开尔文(K)。
二、基本公式1. 牛顿第二定律:F = ma,其中F是物体所受合力的大小,m是物体的质量,a是物体的加速度。
2.功:W=Fs,其中W是力做功的大小,F是力的大小,s是力的方向上物体位移的长度。
3.功率:P=W/t,其中P是功率,W是做的功,t是做功的时间。
4. 动能:K = 1/2 mv2,其中K是物体的动能,m是物体的质量,v是物体的速度。
5. 万有引力定律:F = Gm1m2/r2,其中F是两个物体所受合力的大小,G是万有引力常数(6.67×10-11 Nm2/kg2),m1和m2是两个物体的质量,r是两个物体之间的距离。
三、常见物理常数1.光速:c=3×108m/s,光在真空中传播的速度。
2. 引力常数:G = 6.67×10-11 Nm2/kg2,万有引力定律中的比例常数。
3.电子电荷:e=1.6×10-19C,电荷的基本单位。
4.环境重力加速度:g=9.8m/s2,地球表面上物体受重力的加速度。
5.普朗克常数:h=6.63×10-34J·s,用来描述微观粒子行为的物理常数。
6. 水密度:ρ = 1000 kg/m3,常用的液体密度参考值。
500多个常用化合物物理化学常数表
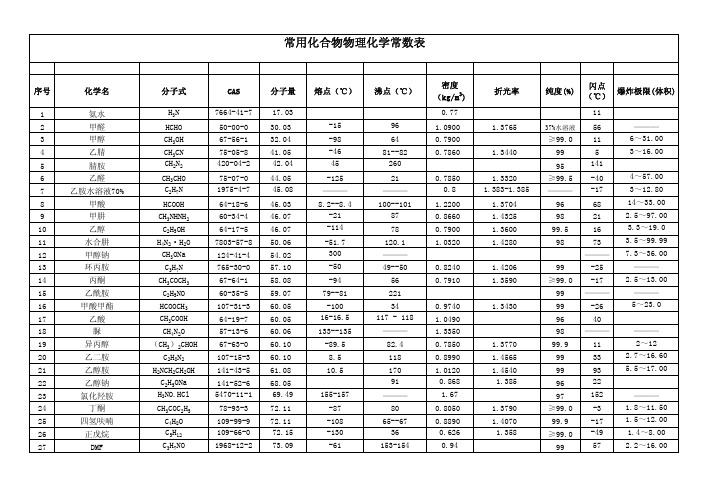
69 164.5--166
130 100-102 76.5--77.5 55--56
130 ——— ——— 114-116
85 229.2 182/20mm 110.6 115--117 77--78
184
0.7070 0.7400 0.9170 0.9320 0.7060
0.78 0.8100 0.9650
110-88-3 110-71-4 110-63-4
56-81-5 108-88-3 106-89-8 109-69-3 62-53-3
90.08 90.12 90.12
92.09 92.14 92.53 92.57 93.13
-50 -49
-80 -98 -116 25-25.5
-90 -85 -111
分子式
H3N
HCHO CH3OH CH3CN CH2N2 CH3CHO C2H7N
HCOOH CH3NHNH2
C2H5OH H4N2·H2O
CH3ONa C3H7N CH3COCH3 C2H5NO HCOOCH3 CH3COOH CH4N2O (CH3)2CHOH C2H8N2 H2NCH2CH2OH C2H5ONa H3NO.HCl CH3COC2H5 C4H8O C5H12 C3H7NO
50
异戊醇
(CH3)2CHC2H4OH 123-51-3
88.15
51
氰化亚铜
CuCN
544-92-3
89.56
52
草酸
HOOCCOOH
144-62-7 90.04
53
三聚甲醛
54
乙二醇二甲醚
55
1,4-丁二醇
56
物理学常量

物理学常量1. 光速(c):在真空中,光速的值约为299,792,458米/秒。
这是一个不可超越的极限速度,也是狭义相对论的基石。
2. 普朗克常数(h):普朗克常数的值约为6.62607015×10^-34 J·s,是量子力学的基础。
它描述了能量的最小单位,即量子。
3. 玻尔兹曼常数(k):玻尔兹曼常数的值约为1.380649×10^-23 J/K,是统计力学中的关键常数,用于描述热运动。
4. 电子电荷(e):电子的电荷大约为1.602176634×10^-19 C,是电磁学的基本单位。
5. 质子质量(m_p):质子的静止质量约为1.672621898×10^-27 kg,是原子物理学和核物理学中的重要参数。
6. 牛顿常数(G):牛顿引力常数的值约为 6.67430×10^-11 N·m^2/kg^2,是描述万有引力的基础。
7. 约化普朗克常数(ħ):约化普朗克常数的值约为1.054571817×10^-34 J·s,是量子力学中的重要常数。
8. 真空介电常数(ε_0):真空介电常数的值约为8.854187817×10^-12 F/m,是电磁学中的基本常数。
9. 微分电荷(e):电子的电荷约为1.602176634×10^-19 C,是电磁学的基本单位。
10. 阿伏伽德罗常数(N_A):阿伏伽德罗常数的值约为6.02214076×10^23 mol^-1,描述了一摩尔物质中分子或原子的数量。
这些常量在物理学各个领域中扮演着关键作用,是构建理论和进行计算的基础。
它们反映了自然界的基本规律和特性。
基本物理常数大全

Fundamental Physical Constants—Adopted valuesRelative std.Quantity Symbol Value Unit uncert.u rrelative atomic mass1of12C A r(12C)12(exact)molar mass constant M u1×10−3kg mol−1(exact)molar mass of12C M(12C)12×10−3kg mol−1(exact)conventional value of Josephson constant2K J−90483597.9GHz V−1(exact)conventional value of von Klitzing constant3R K−9025812.807Ω(exact)standard atmosphere101325Pa(exact)1The relative atomic mass A r(X)of particle X with mass m(X)is defined by A r(X)=m(X)/m u,where m u=m(12C)/12=M u/N A=1u is the atomic mass constant,N A is the Avogadro constant,and u is the atomic mass unit.Thus the mass of particle X in u is m(X)=A r(X)u and the molar mass of X is M(X)=A r(X)M u.2This is the value adopted internationally for realizing representations of the volt using the Josephson effect.3This is the value adopted internationally for realizing representations of the ohm using the quantum Hall effect.Fundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u rGeneralfine-structure constant e2/4π 0¯h cα7.2973525376(50)×10−36.8×10−10 inversefine-structure constantα−1137.035999679(94)6.8×10−10Rydberg constantα2m e c/2h R∞10973731.568527(73)m−16.6×10−12R∞c3.289841960361(22)×1015Hz6.6×10−12R∞hc2.17987197(11)×10−18J5.0×10−8 R∞hc in eV13.60569193(34)eV2.5×10−8Bohr radiusα/4πR∞=4π 0¯h2/m e e2a00.52917720859(36)×10−10m6.8×10−10 Hartree energy e2/4π 0a0=2R∞hc=α2m e c2E h4.35974394(22)×10−18J5.0×10−8 in eV27.21138386(68)eV2.5×10−8 quantum of circulation h/2m e3.6369475199(50)×10−4m2s−11.4×10−9h/m e7.273895040(10)×10−4m2s−11.4×10−9ElectroweakFermi coupling constant1G F/(¯h c)31.16637(1)×10−5GeV−28.6×10−6 weak mixing angle2θW(on-shell scheme)sin2θW=s2≡1−(m W/m Z)2sin2θW0.22255(56)2.5×10−3 WElectron,e−electron mass m e9.10938215(45)×10−31kg5.0×10−8 in u,m e=A r(e)u(electronrelative atomic mass times u)5.4857990943(23)×10−4u4.2×10−10 energy equivalent m e c28.18710438(41)×10−14J5.0×10−8 in MeV0.510998910(13)MeV2.5×10−8electron-muon mass ratio m e/mµ4.83633171(12)×10−32.5×10−8 electron-tau mass ratio m e/mτ2.87564(47)×10−41.6×10−4 electron-proton mass ratio m e/m p5.4461702177(24)×10−44.3×10−10 electron-neutron mass ratio m e/m n5.4386734459(33)×10−46.0×10−10 electron-deuteron mass ratio m e/m d2.7244371093(12)×10−44.3×10−10 electron to alpha particle mass ratio m e/mα1.37093355570(58)×10−44.2×10−10 electron charge to mass quotient−e/m e−1.758820150(44)×1011C kg−12.5×10−8 electron molar mass N A m e M(e),M e5.4857990943(23)×10−7kg mol−14.2×10−10 Compton wavelength h/m e cλC2.4263102175(33)×10−12m1.4×10−9λC/2π=αa0=α2/4πR∞λC386.15926459(53)×10−15m1.4×10−9 classical electron radiusα2a0r e2.8179402894(58)×10−15m2.1×10−9 Thomson cross section(8π/3)r2eσe0.6652458558(27)×10−28m24.1×10−9 electron magnetic momentµe−928.476377(23)×10−26J T−12.5×10−8 to Bohr magneton ratioµe/µB−1.00115965218111(74)7.4×10−13 to nuclear magneton ratioµe/µN−1838.28197092(80)4.3×10−10 electron magnetic momentanomaly|µe|/µB−1a e1.159********(74)×10−36.4×10−10 electron g-factor−2(1+a e)g e−2.0023193043622(15)7.4×10−13electron-muonFundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u r magnetic moment ratioµe/µµ206.7669877(52)2.5×10−8 electron-protonmagnetic moment ratioµe/µp−658.2106848(54)8.1×10−9 electron to shielded protonmagnetic moment ratioµe/µ p−658.2275971(72)1.1×10−8 (H2O,sphere,25◦C)electron-neutronmagnetic moment ratioµe/µn960.92050(23)2.4×10−7 electron-deuteronmagnetic moment ratioµe/µd−2143.923498(18)8.4×10−9 electron to shielded helionmagnetic moment ratioµe/µh 864.058257(10)1.2×10−8(gas,sphere,25◦C)electron gyromagnetic ratio2|µe|/¯hγe1.760859770(44)×1011s−1T−12.5×10−8γe/2π28024.95364(70)MHz T−12.5×10−8Muon,µ−muon mass mµ1.88353130(11)×10−28kg5.6×10−8 in u,mµ=A r(µ)u(muonrelative atomic mass times u)0.1134289256(29)u2.5×10−8 energy equivalent mµc21.692833510(95)×10−11J5.6×10−8 in MeV105.6583668(38)MeV3.6×10−8muon-electron mass ratio mµ/m e206.7682823(52)2.5×10−8 muon-tau mass ratio mµ/mτ5.94592(97)×10−21.6×10−4 muon-proton mass ratio mµ/m p0.1126095261(29)2.5×10−8 muon-neutron mass ratio mµ/m n0.1124545167(29)2.5×10−8 muon molar mass N A mµM(µ),Mµ0.1134289256(29)×10−3kg mol−12.5×10−8muon Compton wavelength h/mµcλC,µ11.73444104(30)×10−15m2.5×10−8λC,µ/2πλC,µ1.867594295(47)×10−15m2.5×10−8 muon magnetic momentµµ−4.49044786(16)×10−26J T−13.6×10−8 to Bohr magneton ratioµµ/µB−4.84197049(12)×10−32.5×10−8 to nuclear magneton ratioµµ/µN−8.89059705(23)2.5×10−8 muon magnetic moment anomaly|µµ|/(e¯h/2mµ)−1aµ1.16592069(60)×10−35.2×10−7 muon g-factor−2(1+aµ)gµ−2.0023318414(12)6.0×10−10 muon-protonmagnetic moment ratioµµ/µp−3.183345137(85)2.7×10−8Tau,τ−tau mass3mτ3.16777(52)×10−27kg1.6×10−4 in u,mτ=A r(τ)u(taurelative atomic mass times u)1.90768(31)u1.6×10−4 energy equivalent mτc22.84705(46)×10−10J1.6×10−4 in MeV1776.99(29)MeV1.6×10−4 tau-electron mass ratio mτ/m e3477.48(57)1.6×10−4Fundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u r tau-muon mass ratio mτ/mµ16.8183(27)1.6×10−4 tau-proton mass ratio mτ/m p1.89390(31)1.6×10−4 tau-neutron mass ratio mτ/m n1.89129(31)1.6×10−4 tau molar mass N A mτM(τ),Mτ1.90768(31)×10−3kg mol−11.6×10−4tau Compton wavelength h/mτcλC,τ0.69772(11)×10−15m1.6×10−4λC,τ/2πλC,τ0.111046(18)×10−15m1.6×10−4Proton,pproton mass m p1.672621637(83)×10−27kg5.0×10−8 in u,m p=A r(p)u(protonrelative atomic mass times u)1.00727646677(10)u1.0×10−10 energy equivalent m p c21.503277359(75)×10−10J5.0×10−8 in MeV938.272013(23)MeV2.5×10−8 proton-electron mass ratio m p/m e1836.15267247(80)4.3×10−10 proton-muon mass ratio m p/mµ8.88024339(23)2.5×10−8 proton-tau mass ratio m p/mτ0.528012(86)1.6×10−4 proton-neutron mass ratio m p/m n0.99862347824(46)4.6×10−10 proton charge to mass quotient e/m p9.57883392(24)×107C kg−12.5×10−8 proton molar mass N A m p M(p),M p1.00727646677(10)×10−3kg mol−11.0×10−10proton Compton wavelength h/m p cλC,p1.3214098446(19)×10−15m1.4×10−9λC,p/2πλC,p0.21030890861(30)×10−15m1.4×10−9 proton rms charge radius R p0.8768(69)×10−15m7.8×10−3 proton magnetic momentµp1.410606662(37)×10−26J T−12.6×10−8 to Bohr magneton ratioµp/µB1.521032209(12)×10−38.1×10−9 to nuclear magneton ratioµp/µN2.792847356(23)8.2×10−9 proton g-factor2µp/µN g p5.585694713(46)8.2×10−9 proton-neutronmagnetic moment ratioµp/µn−1.45989806(34)2.4×10−7 shielded proton magnetic momentµ p1.410570419(38)×10−26J T−12.7×10−8 (H2O,sphere,25◦C)to Bohr magneton ratioµ p/µB1.520993128(17)×10−31.1×10−8 to nuclear magneton ratioµ p/µN2.792775598(30)1.1×10−8 proton magnetic shieldingcorrection1−µ p/µpσ p25.694(14)×10−65.3×10−4 (H2O,sphere,25◦C)proton gyromagnetic ratio2µp/¯hγp2.675222099(70)×108s−1T−12.6×10−8γp/2π42.5774821(11)MHz T−12.6×10−8 shielded proton gyromagneticratio2µ p/¯hγ p2.675153362(73)×108s−1T−12.7×10−8 (H2O,sphere,25◦C)γ p/2π42.5763881(12)MHz T−12.7×10−8Neutron,nneutron mass m n1.674927211(84)×10−27kg5.0×10−8 in u,m n=A r(n)u(neutronFundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u r relative atomic mass times u)1.00866491597(43)u4.3×10−10 energy equivalent m n c21.505349505(75)×10−10J5.0×10−8 in MeV939.565346(23)MeV2.5×10−8neutron-electron mass ratio m n/m e1838.6836605(11)6.0×10−10 neutron-muon mass ratio m n/mµ8.89248409(23)2.5×10−8 neutron-tau mass ratio m n/mτ0.528740(86)1.6×10−4 neutron-proton mass ratio m n/m p1.00137841918(46)4.6×10−10 neutron molar mass N A m n M(n),M n1.00866491597(43)×10−3kg mol−14.3×10−10 neutron Compton wavelength h/m n cλC,n1.3195908951(20)×10−15m1.5×10−9λC,n/2πλC,n0.21001941382(31)×10−15m1.5×10−9 neutron magnetic momentµn−0.96623641(23)×10−26J T−12.4×10−7 to Bohr magneton ratioµn/µB−1.04187563(25)×10−32.4×10−7 to nuclear magneton ratioµn/µN−1.91304273(45)2.4×10−7 neutron g-factor2µn/µN g n−3.82608545(90)2.4×10−7 neutron-electronmagnetic moment ratioµn/µe1.04066882(25)×10−32.4×10−7 neutron-protonmagnetic moment ratioµn/µp−0.68497934(16)2.4×10−7 neutron to shielded protonmagnetic moment ratioµn/µ p−0.68499694(16)2.4×10−7 (H2O,sphere,25◦C)neutron gyromagnetic ratio2|µn|/¯hγn1.83247185(43)×108s−1T−12.4×10−7γn/2π29.1646954(69)MHz T−12.4×10−7Deuteron,ddeuteron mass m d3.34358320(17)×10−27kg5.0×10−8 in u,m d=A r(d)u(deuteronrelative atomic mass times u)2.013553212724(78)u3.9×10−11 energy equivalent m d c23.00506272(15)×10−10J5.0×10−8 in MeV1875.612793(47)MeV2.5×10−8 deuteron-electron mass ratio m d/m e3670.4829654(16)4.3×10−10 deuteron-proton mass ratio m d/m p1.99900750108(22)1.1×10−10 deuteron molar mass N A m d M(d),M d2.013553212724(78)×10−3kg mol−13.9×10−11deuteron rms charge radius R d2.1402(28)×10−15m1.3×10−3 deuteron magnetic momentµd0.433073465(11)×10−26J T−12.6×10−8 to Bohr magneton ratioµd/µB0.4669754556(39)×10−38.4×10−9 to nuclear magneton ratioµd/µN0.8574382308(72)8.4×10−9 deuteron g-factorµd/µN g d0.8574382308(72)8.4×10−9 deuteron-electronmagnetic moment ratioµd/µe−4.664345537(39)×10−48.4×10−9 deuteron-protonmagnetic moment ratioµd/µp0.3070122070(24)7.7×10−9 deuteron-neutronFundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u rmagnetic moment ratioµd/µn−0.44820652(11)2.4×10−7Triton,ttriton mass m t5.00735588(25)×10−27kg5.0×10−8 in u,m t=A r(t)u(tritonrelative atomic mass times u)3.0155007134(25)u8.3×10−10 energy equivalent m t c24.50038703(22)×10−10J5.0×10−8 in MeV2808.920906(70)MeV2.5×10−8 triton-electron mass ratio m t/m e5496.9215269(51)9.3×10−10 triton-proton mass ratio m t/m p2.9937170309(25)8.4×10−10 triton molar mass N A m t M(t),M t3.0155007134(25)×10−3kg mol−18.3×10−10triton magnetic momentµt1.504609361(42)×10−26J T−12.8×10−8 to Bohr magneton ratioµt/µB1.622393657(21)×10−31.3×10−8 to nuclear magneton ratioµt/µN2.978962448(38)1.3×10−8 triton g-factor2µt/µN g t5.957924896(76)1.3×10−8 triton-electronmagnetic moment ratioµt/µe−1.620514423(21)×10−31.3×10−8 triton-protonmagnetic moment ratioµt/µp1.066639908(10)9.8×10−9 triton-neutronmagnetic moment ratioµt/µn−1.55718553(37)2.4×10−7Helion,hhelion mass4m h5.00641192(25)×10−27kg5.0×10−8 in u,m h=A r(h)u(helionrelative atomic mass times u)3.0149322473(26)u8.6×10−10 energy equivalent m h c24.49953864(22)×10−10J5.0×10−8 in MeV2808.391383(70)MeV2.5×10−8 helion-electron mass ratio m h/m e5495.8852765(52)9.5×10−10 helion-proton mass ratio m h/m p2.9931526713(26)8.7×10−10 helion molar mass N A m h M(h),M h3.0149322473(26)×10−3kg mol−18.6×10−10shielded helion magnetic momentµh −1.074552982(30)×10−26J T−12.8×10−8(gas,sphere,25◦C)to Bohr magneton ratioµh /µB−1.158671471(14)×10−31.2×10−8to nuclear magneton ratioµh /µN−2.127497718(25)1.2×10−8shielded helion to protonmagnetic moment ratioµh /µp−0.761766558(11)1.4×10−8(gas,sphere,25◦C)shielded helion to shielded protonmagnetic moment ratioµh /µ p−0.7617861313(33)4.3×10−9(gas/H2O,spheres,25◦C) shielded helion gyromagneticratio2|µh |/¯hγh2.037894730(56)×108s−1T−12.8×10−8(gas,sphere,25◦C)γh/2π32.43410198(90)MHz T−12.8×10−8Fundamental Physical Constants—Atomic and Nuclear ConstantsRelative std.Quantity Symbol Value Unit uncert.u rAlpha particle,αalpha particle mass mα6.64465620(33)×10−27kg5.0×10−8 in u,mα=A r(α)u(alpha particlerelative atomic mass times u)4.001506179127(62)u1.5×10−11 energy equivalent mαc25.97191917(30)×10−10J5.0×10−8 in MeV3727.379109(93)MeV2.5×10−8alpha particle to electron mass ratio mα/m e7294.2995365(31)4.2×10−10alpha particle to proton mass ratio mα/m p3.97259968951(41)1.0×10−10alpha particle molar mass N A mαM(α),Mα4.001506179127(62)×10−3kg mol−11.5×10−111Value recommended by the Particle Data Group(Yao,et al.,2006).2Based on the ratio of the masses of the W and Z bosons m W/m Z recommended by the Particle Data Group(Yao,et al.,2006).The value for sin2θW they recommend,which is based on a particular variant of the modified minimal subtraction(MS)scheme,is sin2ˆθW(M Z)=0.23122(15). 3This and all other values involving mτare based on the value of mτc2in MeV recommended by the Particle Data Group(Yao,et al.,2006),but with a standard uncertainty of0.29MeV rather than the quoted uncertainty of−0.26MeV,+0.29MeV.4The helion,symbol h,is the nucleus of the3He atom.Fundamental Physical Constants—Electromagnetic constantsRelative std.Quantity Symbol Value Unit uncert.u relementary charge e1.602176487(40)×10−19C2.5×10−8e/h2.417989454(60)×1014A J−12.5×10−8magneticflux quantum h/2eΦ02.067833667(52)×10−15Wb2.5×10−8conductance quantum2e2/h G07.7480917004(53)×10−5S6.8×10−10 inverse of conductance quantum G−1012906.4037787(88)Ω6.8×10−10Josephson constant12e/h K J483597.891(12)×109Hz V−12.5×10−8von Klitzing constant2h/e2=µ0c/2αR K25812.807557(18)Ω6.8×10−10Bohr magneton e¯h/2m eµB927.400915(23)×10−26J T−12.5×10−8 in eV T−15.7883817555(79)×10−5eV T−11.4×10−9µB/h13.99624604(35)×109Hz T−12.5×10−8µB/hc46.6864515(12)m−1T−12.5×10−8µB/k0.6717131(12)K T−11.7×10−6nuclear magneton e¯h/2m pµN5.05078324(13)×10−27J T−12.5×10−8 in eV T−13.1524512326(45)×10−8eV T−11.4×10−9µN/h7.62259384(19)MHz T−12.5×10−8µN/hc2.542623616(64)×10−2m−1T−12.5×10−8µN/k3.6582637(64)×10−4K T−11.7×10−61See the“Adopted values”table for the conventional value adopted internationally for realizing representations of the volt using the Joseph-son effect.2See the“Adopted values”table for the conventional value adopted internationally for realizing representations of the ohm using the quantum Hall effect.Fundamental Physical Constants —Extensive ListingRelative std.QuantitySymbolValueUnituncert.u rUNIVERSAL speed of light in vacuum c,c 0299792458m s −1(exact)magnetic constant µ04π×10−7N A −2=12.566370614...×10−7N A −2(exact)electric constant 1/µ0c 208.854187817...×10−12F m −1(exact)characteristic impedance of vacuumµ0/ 0=µ0c Z 0376.730313461...Ω(exact)Newtonian constant of gravitation G 6.67428(67)×10−11m 3kg −1s −21.0×10−4G/¯h c 6.70881(67)×10−39(GeV /c 2)−21.0×10−4Planck constanth 6.62606896(33)×10−34J s 5.0×10−8in eV s 4.13566733(10)×10−15eV s 2.5×10−8h/2π¯h1.054571628(53)×10−34J s 5.0×10−8in eV s 6.58211899(16)×10−16eV s2.5×10−8¯h c in MeV fm197.3269631(49)MeV fm 2.5×10−8Planck mass (¯h c/G )1/2m P 2.17644(11)×10−8kg 5.0×10−5energy equivalent in GeV m P c 21.220892(61)×1019GeV 5.0×10−5Planck temperature (¯h c 5/G )1/2/k T P 1.416785(71)×1032K 5.0×10−5Planck length ¯h /m P c =(¯h G/c 3)1/2l P 1.616252(81)×10−35m 5.0×10−5Planck time l P /c =(¯h G/c 5)1/2t P5.39124(27)×10−44s 5.0×10−5ELECTROMAGNETIC elementary chargee 1.602176487(40)×10−19C 2.5×10−8e/h 2.417989454(60)×1014A J −12.5×10−8magnetic flux quantum h/2e Φ02.067833667(52)×10−15Wb 2.5×10−8conductance quantum 2e 2/hG 07.7480917004(53)×10−5S 6.8×10−10inverse of conductance quantum G −1012906.4037787(88)Ω6.8×10−10Josephson constant 12e/h K J 483597.891(12)×109Hz V −12.5×10−8von Klitzing constant 2h/e 2=µ0c/2αR K 25812.807557(18)Ω6.8×10−10Bohr magneton e ¯h /2m eµB 927.400915(23)×10−26J T −12.5×10−8in eV T−15.7883817555(79)×10−5eV T −11.4×10−9µB /h 13.99624604(35)×109Hz T −12.5×10−8µB /hc 46.6864515(12)m −1T −12.5×10−8µB /k0.6717131(12)K T −11.7×10−6nuclear magneton e ¯h /2m pµN 5.05078324(13)×10−27J T −12.5×10−8in eV T−13.1524512326(45)×10−8eV T −11.4×10−9µN /h 7.62259384(19)MHz T −12.5×10−8µN /hc 2.542623616(64)×10−2m −1T −12.5×10−8µN /k3.6582637(64)×10−4K T −11.7×10−6ATOMIC AND NUCLEARGeneralfine-structure constant e 2/4π 0¯h c α7.2973525376(50)×10−36.8×10−10inverse fine-structure constantα−1137.035999679(94)6.8×10−10Fundamental Physical Constants—Extensive ListingRelative std.Quantity Symbol Value Unit uncert.u r Rydberg constantα2m e c/2h R∞10973731.568527(73)m−16.6×10−12R∞c3.289841960361(22)×1015Hz6.6×10−12R∞hc2.17987197(11)×10−18J5.0×10−8 R∞hc in eV13.60569193(34)eV2.5×10−8Bohr radiusα/4πR∞=4π 0¯h2/m e e2a00.52917720859(36)×10−10m6.8×10−10 Hartree energy e2/4π 0a0=2R∞hc=α2m e c2E h4.35974394(22)×10−18J5.0×10−8 in eV27.21138386(68)eV2.5×10−8 quantum of circulation h/2m e3.6369475199(50)×10−4m2s−11.4×10−9h/m e7.273895040(10)×10−4m2s−11.4×10−9ElectroweakFermi coupling constant3G F/(¯h c)31.16637(1)×10−5GeV−28.6×10−6 weak mixing angle4θW(on-shell scheme)≡1−(m W/m Z)2sin2θW0.22255(56)2.5×10−3 sin2θW=s2WElectron,e−electron mass m e9.10938215(45)×10−31kg5.0×10−8 in u,m e=A r(e)u(electronrelative atomic mass times u)5.4857990943(23)×10−4u4.2×10−10 energy equivalent m e c28.18710438(41)×10−14J5.0×10−8 in MeV0.510998910(13)MeV2.5×10−8electron-muon mass ratio m e/mµ4.83633171(12)×10−32.5×10−8 electron-tau mass ratio m e/mτ2.87564(47)×10−41.6×10−4 electron-proton mass ratio m e/m p5.4461702177(24)×10−44.3×10−10 electron-neutron mass ratio m e/m n5.4386734459(33)×10−46.0×10−10 electron-deuteron mass ratio m e/m d2.7244371093(12)×10−44.3×10−10 electron to alpha particle mass ratio m e/mα1.37093355570(58)×10−44.2×10−10electron charge to mass quotient−e/m e−1.758820150(44)×1011C kg−12.5×10−8 electron molar mass N A m e M(e),M e5.4857990943(23)×10−7kg mol−14.2×10−10 Compton wavelength h/m e cλC2.4263102175(33)×10−12m1.4×10−9λC/2π=αa0=α2/4πR∞λC386.15926459(53)×10−15m1.4×10−9 classical electron radiusα2a0r e2.8179402894(58)×10−15m2.1×10−9 Thomson cross section(8π/3)r2eσe0.6652458558(27)×10−28m24.1×10−9 electron magnetic momentµe−928.476377(23)×10−26J T−12.5×10−8 to Bohr magneton ratioµe/µB−1.00115965218111(74)7.4×10−13 to nuclear magneton ratioµe/µN−1838.28197092(80)4.3×10−10 electron magnetic momentanomaly|µe|/µB−1a e1.159********(74)×10−36.4×10−10 electron g-factor−2(1+a e)g e−2.0023193043622(15)7.4×10−13 electron-muonmagnetic moment ratioµe/µµ206.7669877(52)2.5×10−8 electron-protonmagnetic moment ratioµe/µp−658.2106848(54)8.1×10−9Fundamental Physical Constants—Extensive ListingRelative std.Quantity Symbol Value Unit uncert.u r electron to shielded protonmagnetic moment ratioµe/µ p−658.2275971(72)1.1×10−8 (H2O,sphere,25◦C)electron-neutronmagnetic moment ratioµe/µn960.92050(23)2.4×10−7 electron-deuteronmagnetic moment ratioµe/µd−2143.923498(18)8.4×10−9 electron to shielded helionmagnetic moment ratioµe/µh 864.058257(10)1.2×10−8(gas,sphere,25◦C)electron gyromagnetic ratio2|µe|/¯hγe1.760859770(44)×1011s−1T−12.5×10−8γe/2π28024.95364(70)MHz T−12.5×10−8Muon,µ−muon mass mµ1.88353130(11)×10−28kg5.6×10−8 in u,mµ=A r(µ)u(muonrelative atomic mass times u)0.1134289256(29)u2.5×10−8 energy equivalent mµc21.692833510(95)×10−11J5.6×10−8 in MeV105.6583668(38)MeV3.6×10−8muon-electron mass ratio mµ/m e206.7682823(52)2.5×10−8 muon-tau mass ratio mµ/mτ5.94592(97)×10−21.6×10−4 muon-proton mass ratio mµ/m p0.1126095261(29)2.5×10−8 muon-neutron mass ratio mµ/m n0.1124545167(29)2.5×10−8 muon molar mass N A mµM(µ),Mµ0.1134289256(29)×10−3kg mol−12.5×10−8muon Compton wavelength h/mµcλC,µ11.73444104(30)×10−15m2.5×10−8λC,µ/2πλC,µ1.867594295(47)×10−15m2.5×10−8 muon magnetic momentµµ−4.49044786(16)×10−26J T−13.6×10−8 to Bohr magneton ratioµµ/µB−4.84197049(12)×10−32.5×10−8 to nuclear magneton ratioµµ/µN−8.89059705(23)2.5×10−8 muon magnetic moment anomaly|µµ|/(e¯h/2mµ)−1aµ1.16592069(60)×10−35.2×10−7 muon g-factor−2(1+aµ)gµ−2.0023318414(12)6.0×10−10 muon-protonmagnetic moment ratioµµ/µp−3.183345137(85)2.7×10−8Tau,τ−tau mass5mτ3.16777(52)×10−27kg1.6×10−4 in u,mτ=A r(τ)u(taurelative atomic mass times u)1.90768(31)u1.6×10−4 energy equivalent mτc22.84705(46)×10−10J1.6×10−4 in MeV1776.99(29)MeV1.6×10−4 tau-electron mass ratio mτ/m e3477.48(57)1.6×10−4 tau-muon mass ratio mτ/mµ16.8183(27)1.6×10−4 tau-proton mass ratio mτ/m p1.89390(31)1.6×10−4 tau-neutron mass ratio mτ/m n1.89129(31)1.6×10−4Fundamental Physical Constants—Extensive ListingRelative std.Quantity Symbol Value Unit uncert.u r tau molar mass N A mτM(τ),Mτ1.90768(31)×10−3kg mol−11.6×10−4 tau Compton wavelength h/mτcλC,τ0.69772(11)×10−15m1.6×10−4λC,τ/2πλC,τ0.111046(18)×10−15m1.6×10−4Proton,pproton mass m p1.672621637(83)×10−27kg5.0×10−8 in u,m p=A r(p)u(protonrelative atomic mass times u)1.00727646677(10)u1.0×10−10 energy equivalent m p c21.503277359(75)×10−10J5.0×10−8 in MeV938.272013(23)MeV2.5×10−8 proton-electron mass ratio m p/m e1836.15267247(80)4.3×10−10 proton-muon mass ratio m p/mµ8.88024339(23)2.5×10−8 proton-tau mass ratio m p/mτ0.528012(86)1.6×10−4 proton-neutron mass ratio m p/m n0.99862347824(46)4.6×10−10 proton charge to mass quotient e/m p9.57883392(24)×107C kg−12.5×10−8 proton molar mass N A m p M(p),M p1.00727646677(10)×10−3kg mol−11.0×10−10proton Compton wavelength h/m p cλC,p1.3214098446(19)×10−15m1.4×10−9λC,p/2πλC,p0.21030890861(30)×10−15m1.4×10−9 proton rms charge radius R p0.8768(69)×10−15m7.8×10−3 proton magnetic momentµp1.410606662(37)×10−26J T−12.6×10−8 to Bohr magneton ratioµp/µB1.521032209(12)×10−38.1×10−9 to nuclear magneton ratioµp/µN2.792847356(23)8.2×10−9 proton g-factor2µp/µN g p5.585694713(46)8.2×10−9 proton-neutronmagnetic moment ratioµp/µn−1.45989806(34)2.4×10−7 shielded proton magnetic momentµ p1.410570419(38)×10−26J T−12.7×10−8 (H2O,sphere,25◦C)to Bohr magneton ratioµ p/µB1.520993128(17)×10−31.1×10−8 to nuclear magneton ratioµ p/µN2.792775598(30)1.1×10−8 proton magnetic shieldingcorrection1−µ p/µpσ p25.694(14)×10−65.3×10−4 (H2O,sphere,25◦C)proton gyromagnetic ratio2µp/¯hγp2.675222099(70)×108s−1T−12.6×10−8γp/2π42.5774821(11)MHz T−12.6×10−8 shielded proton gyromagneticratio2µ p/¯hγ p2.675153362(73)×108s−1T−12.7×10−8 (H2O,sphere,25◦C)γ p/2π42.5763881(12)MHz T−12.7×10−8Neutron,nneutron mass m n1.674927211(84)×10−27kg5.0×10−8 in u,m n=A r(n)u(neutronrelative atomic mass times u)1.00866491597(43)u4.3×10−10 energy equivalent m n c21.505349505(75)×10−10J5.0×10−8 in MeV939.565346(23)MeV2.5×10−8Fundamental Physical Constants—Extensive ListingRelative std.Quantity Symbol Value Unit uncert.u r neutron-electron mass ratio m n/m e1838.6836605(11)6.0×10−10 neutron-muon mass ratio m n/mµ8.89248409(23)2.5×10−8 neutron-tau mass ratio m n/mτ0.528740(86)1.6×10−4 neutron-proton mass ratio m n/m p1.00137841918(46)4.6×10−10 neutron molar mass N A m n M(n),M n1.00866491597(43)×10−3kg mol−14.3×10−10neutron Compton wavelength h/m n cλC,n1.3195908951(20)×10−15m1.5×10−9λC,n/2πλC,n0.21001941382(31)×10−15m1.5×10−9 neutron magnetic momentµn−0.96623641(23)×10−26J T−12.4×10−7 to Bohr magneton ratioµn/µB−1.04187563(25)×10−32.4×10−7 to nuclear magneton ratioµn/µN−1.91304273(45)2.4×10−7neutron g-factor2µn/µN g n−3.82608545(90)2.4×10−7 neutron-electronmagnetic moment ratioµn/µe1.04066882(25)×10−32.4×10−7 neutron-protonmagnetic moment ratioµn/µp−0.68497934(16)2.4×10−7 neutron to shielded protonmagnetic moment ratioµn/µ p−0.68499694(16)2.4×10−7 (H2O,sphere,25◦C)neutron gyromagnetic ratio2|µn|/¯hγn1.83247185(43)×108s−1T−12.4×10−7γn/2π29.1646954(69)MHz T−12.4×10−7Deuteron,ddeuteron mass m d3.34358320(17)×10−27kg5.0×10−8 in u,m d=A r(d)u(deuteronrelative atomic mass times u)2.013553212724(78)u3.9×10−11 energy equivalent m d c23.00506272(15)×10−10J5.0×10−8 in MeV1875.612793(47)MeV2.5×10−8 deuteron-electron mass ratio m d/m e3670.4829654(16)4.3×10−10 deuteron-proton mass ratio m d/m p1.99900750108(22)1.1×10−10 deuteron molar mass N A m d M(d),M d2.013553212724(78)×10−3kg mol−13.9×10−11deuteron rms charge radius R d2.1402(28)×10−15m1.3×10−3 deuteron magnetic momentµd0.433073465(11)×10−26J T−12.6×10−8 to Bohr magneton ratioµd/µB0.4669754556(39)×10−38.4×10−9 to nuclear magneton ratioµd/µN0.8574382308(72)8.4×10−9 deuteron g-factorµd/µN g d0.8574382308(72)8.4×10−9 deuteron-electronmagnetic moment ratioµd/µe−4.664345537(39)×10−48.4×10−9 deuteron-protonmagnetic moment ratioµd/µp0.3070122070(24)7.7×10−9 deuteron-neutronmagnetic moment ratioµd/µn−0.44820652(11)2.4×10−7Triton,ttriton mass m t5.00735588(25)×10−27kg5.0×10−8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
25个物理常数
篇一:
标题: 25个物理常数(创建与标题相符的正文并拓展)
正文:
物理学是研究自然现象的科学,其基础是一些基本常数。
这些常数是通过对自然界的观察和实验得出的,它们对物理学的理论和实践具有至关重要的影响。
本文将介绍25个基本的物理学常数,包括它们的值、定义和意义。
1. 开尔文(k)
开尔文(k)是一个常量,它的值为1.19264×10-19J/(K·K)。
它是电离常数,用于描述电解质的电离程度。
2. 普朗克常数(h)
普朗克常数(h)是一个基本的物理学常数,它的值为6.626176×
10-35J/(K·s)。
它是热力学中的基本常数,用于描述能量和热量之间的关系。
3. 光速(c)
光速(c)是一个基本的物理学常数,它的值为299,792,458米/秒。
它是真空中光的速度,也是宇宙中最基本的速度。
4. 磁感应强度(B)
磁感应强度(B)是一个物理学常数,用于描述磁场的强度。
它的值通常在0到1000特斯拉之间,磁感应强度越大,磁场越强。
5. 电容(C)
电容(C)是一个物理学常数,用于描述电容器的电容值。
它的值通常在0到1特斯拉之间,电容器的电容值越大,电容器的储存电能的能力越强。
6. 电阻(R)
电阻(R)是一个物理学常数,用于描述导体的电阻值。
它的值通常在0到无穷大之间,电阻值越大,导体的电阻能力越强。
7. 温度(T)
温度(T)是物理学中的基本常数,用于描述物体的状态。
它的值通常在0到开尔文之间,温度越高,物体的状态越热。
8. 引力(G)
引力(G)是物理学中的基本常数,用于描述物体之间的引力大小。
它的值通常在6.6743×10-11N·(m/kg)^2。
9. 电磁场频率(E)
电磁场频率(E)是物理学常数,用于描述电磁场的传播速度。
它的值通常在真空中约为3×10^10米/秒。
10. 质能关系(E=mc2)
质能关系(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。
这个公式表明,质量可以被转化为能量,反之亦然。
11. 原子核能级(E=mc2)
原子核能级(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。
这个公式表明,质量可以被转化为能量,反之亦然。
12. 量子力学(H)
量子力学(H)是物理学中的一个重要分支,用于描述微观世界中的粒子和波动的行为。
13. 电势(V)
电势(V)是物理学中的基本常数,用于描述电场的电势。
它的值通常在0到真空中的电势差之间。
14. 磁通量(Q)
磁通量(Q)是物理学中的基本常数,用于描述磁场中的磁通量。
它的值通常在0到1特斯拉之间。
15. 自旋(S)
自旋(S)是物理学中的基本常数,用于描述原子核中的电子的自旋方向。
16. 电偶极矩(M)
电偶极矩(M)是物理学中的基本常数,用于描述带电物体的电偶极矩。
它的值通常在物体的电荷量与电偶极矩的乘积的开根号内。
17. 能级(N)
能级(N)是物理学中的基本常数,用于描述物质的能量分布。
它的值通常在0到无穷大之间。
18. 原子序数(N)
原子序数(N)是物理学中的基本常数,用于描述元素的原子序数。
19. 热力学第二定律(N2)
热力学第二定律(N2)是物理学中的一个重要定律,用于描述热力学系统的状态和演化。
20. 熵(S)
熵(S)是物理学中的基本常数,用于描述系统的无序程度。
它的值通常在0到1之间。
21. 量子力学中的角动量(P)
量子力学中的角动量(P)是物理学中的一个重要公式,用于描述粒子的角动量。
22. 磁场强度(B)
磁场强度(B)是物理学中的基本常数,用于描述磁场的强度。
它的值通常在0到100特斯拉之间。
23. 磁导率(D)
磁导率(D)是物理学中的基本常数,用于描述磁介质的磁导率。
它的值通常在0到1特斯拉/米之间。
24. 光速不变原理(C=299,792,458m/s)
光速不变原理(C=299,792,458m/s)是物理学中的一个重要原理,用于描述光速在真空中的数值。
25. 国际单位制(SI)
国际单位制(SI)是物理学中的一个重要体系,用于描述物理量的基本单位。
篇二:
标题: 25个物理常数(创建与标题相符的正文并拓展)
正文:
物理学是研究物质、能量、力和运动等基本规律的学科。
在物理学中,有许多基本常数,这些常数对物理学的发展和实验结果的验证都有着重要的影响。
本文将介绍25个常用的物理常数,包括它们的值、定义和来源等。
1. 开普勒常数(K)
开普勒常数是物理学中最基本的常数之一,其值为 299792458。
它是用来描述行星轨道半径大小的标准值。
2. 光速(c)
光速是物理学中最基本的速度,其值为 299792458 m/s。
它是目前已知的最快速的速度,也是相对论中的重要常数之一。
3. 质能关系式(E=mc2)
质能关系式是爱因斯坦提出的,它表示质量和能量是等价的。
这个关系式表明,一个物体的质量可以通过核反应释放出大量的能量,而能量也可以通过物体的质量释放。
4. 磁感应强度(B)
磁感应强度是描述磁场强度的常数,其值为 2πnπA/m(其中 n 是磁导率,A 是磁感应强度,m 是磁体质量)。
磁感应强度的单位是特斯拉(T)。
5. 电容(C)
电容是描述电容器的常数,其值为 2πfC。
电容的单位是安培(A)。
6. 电感(L)
电感是描述电感器的常数,其值为 L。
电感的单位是安培/米(A/m)。
7. 电阻(R)
电阻是描述导体或绝缘体的常数,其值为 R。
电阻的单位是欧姆(Ω)。
8. 磁导率(n)
磁导率是描述磁场导率的常数,其值为 n。
磁导率的单位是特斯拉/米(T/m)。
9. 弹性模量(E)
弹性模量是描述物体弹性的常数,其值为 E。
弹性模量的单位是牛顿/平方米(N/m2)。
10. 引力常数(G)
引力常数是物理学中最基本的常数之一,其值为 6.67408 × 10-11 N·(m/kg)^2。
它是万有引力定律的常数,用来描述物体间的引力。
11. 原子核外电子数(n)
原子核外电子数是描述原子核外电子数量的常数,其值为 20。
12. 质子数(n)
质子数是描述质子数量的常数,其值为 10。
13. 电子电荷数(e)
电子电荷数是描述电子电荷数量的常数,其值为 1.6021766 × 10-19 C。
14. 原子核电荷数(q)
原子核电荷数是描述原子核电荷数量的常数,其值为 1.6021766 × 10-19 C。
15. 原子序数(Z)
原子序数是描述原子核内质子数数量的常数,其值为 10。
16. 磁化强度(B)
磁化强度是描述磁场磁化程度的常数,其值为 B。
17. 电化强度(A)
电化强度是描述电场电化程度的常数,其值为 A。
18. 磁化率(B)
磁化率是描述磁场磁化程度的常数,其值为 B/A。
19. 光速平方(v2)
光速平方是描述光速变化的常数,其值为 299792458。
20. 磁通量(Q)
磁通量是描述磁场通量的常数,其值为 4πnπA/m。
21. 电通量(Q)
电通量是描述电场通量的常数,其值为 4πeA。
22. 磁通密度(D)
磁通密度是描述磁通量的单位,其值为 D。
23. 磁导率(n)
磁导率是描述磁场导率的常数,其值为 n。
24. 磁化强度(B)
磁化强度是描述磁场磁化程度的常数,其值为 B。
25. 电化强度(A)
电化强度是描述电场电化程度的常数,其值为 A。
拓展:
除了这25个物理常数外,还有一些其他的物理常数,例如万有引力常数 G、电荷分布系数、角动量守恒常数等,这些常数也对于物理学的发展和实验结果的验证有着重要的影响。
这些物理常数是物理学的基础,它们在宇宙中的演化和物质运动的研究中都发挥着重要的作用。
了解这些常数的值、定义和来源,有助于我们更好地理解自然界的奥秘。
