武汉理工控制工程第五章习题答案
武汉理工大学材料成型控制工程基础试题
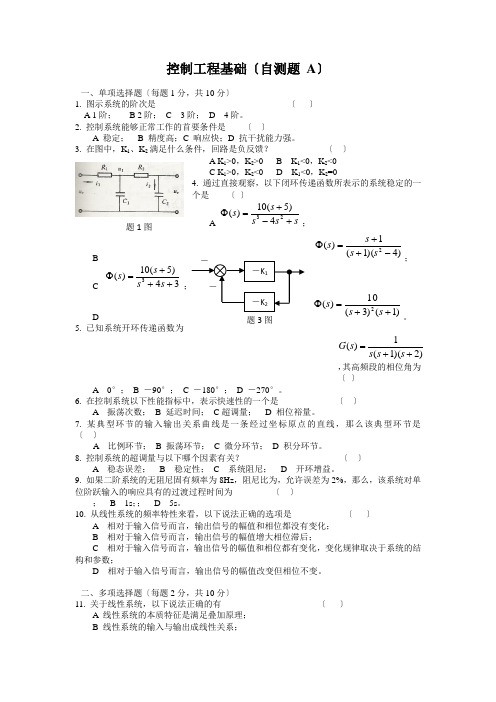
控制工程基础〔自测题 A 〕一、单项选择题〔每题1分,共10分〕1. 图示系统的阶次是 〔 〕 A 1阶; B 2阶; C 3阶; D 4阶。
2. 控制系统能够正常工作的首要条件是 〔 〕A 稳定;B 精度高;C 响应快;D 抗干扰能力强。
3. 在图中,K 1、K 2满足什么条件,回路是负反馈? 〔 〕A K 1>0,K 2>0B K 1<0,K 2<0C K 1>0,K 2<0D K 1<0,K 2=04. 通过直接观察,以下闭环传递函数所表示的系统稳定的一个是 〔 〕A;;BC ;。
D5. 已知系统开环传递函数为,其高频段的相位角为 〔 〕A 0°;B -90°;C -180°;D -270°。
6. 在控制系统以下性能指标中,表示快速性的一个是 〔 〕 A 振荡次数; B 延迟时间; C 超调量; D 相位裕量。
7. 某典型环节的输入输出关系曲线是一条经过坐标原点的直线,那么该典型环节是 〔 〕A 比例环节;B 振荡环节;C 微分环节;D 积分环节。
8. 控制系统的超调量与以下哪个因素有关? 〔 〕A 稳态误差;B 稳定性;C 系统阻尼;D 开环增益。
9. 如果二阶系统的无阻尼固有频率为8Hz ,阻尼比为,允许误差为2%,那么,该系统对单位阶跃输入的响应具有的过渡过程时间为 〔 〕; B 1s ;; D 5s 。
10. 从线性系统的频率特性来看,以下说法正确的选项是 〔 〕A 相对于输入信号而言,输出信号的幅值和相位都没有变化;B 相对于输入信号而言,输出信号的幅值增大相位滞后;C 相对于输入信号而言,输出信号的幅值和相位都有变化,变化规律取决于系统的结构和参数;D 相对于输入信号而言,输出信号的幅值改变但相位不变。
二、多项选择题〔每题2分,共10分〕11. 关于线性系统,以下说法正确的有 〔 〕A 线性系统的本质特征是满足叠加原理;B 线性系统的输入与输出成线性关系;s s s s s +-+=Φ234)5(10)()4)(1(1)(2-++=Φs s s s 34)5(10)(3+++=Φs s s s )1()3(10)(2++=Φs s s )2)(1(1)(++=s s s s G 题1图-K 1-K 2 --题3图C 描述线性系统的微分方程中,各项系数均与系统的输入输出信号及其导数无关;D 描述线性系统的微分方程中,各项系数均与时间无关;E 线性系统都可以用传递函数描述。
武汉理工大学-机械工程控制基础(新)

一、单选(共计50分,每题2.5分)1、临界阻尼二阶系统的单位阶跃稳态响应为()。
C. 单调上升曲线2、关于反馈的说法,正确的是()。
C. 反馈就是将输出信号以不同方式作用于系统3、单位反馈控制系统的开环传递函数,则其闭环传递函数为()。
A.4、在开环频域性能指标中,幅值穿越频率越大,则控制系统()。
B. 响应越快5、某系统的传递函数为,则其频率特性的幅频特性为()。
B.6、某系统传递函数的特征多项式为,式中均为大于0的常数,则系统稳定的条件是()。
C.7、在对系统进行频域分析时,以Bode图为基础,若要提高系统的抗干扰能力,应采取()的措施。
8、某系统为Ⅰ型系统,要使该系统的稳态误差为0,则其输入信号为()。
9、欠阻尼二阶系统的无阻尼自由振荡频率越大,系统()越好。
B. 快速响应性能10、某象函数,其原函数()。
D.11、在阶跃信号输入作用下,阻尼比()的二阶系统,其响应具有幅值逐渐衰减的振荡特性。
D.12、()是衡量系统的准确性的。
C. 稳态误差13、闭环控制系统是指系统中有()。
14、某原函数,则其象函数()。
B.15、某系统的传递函数,当输入时,则其稳态输出的幅值为()。
B.16、对于传递函数难以获得的控制系统,可以采用系统辨识的方法,即(),从而间接获得该系统的传递函数。
B. 输入正弦信号,根据其稳态输出,确定其频率特性17、过阻尼二阶系统的单位阶跃稳态响应为()。
C. 单调上升曲线18、在控制系统中,信号的传递都为连续信号,则该系统属于()系统。
C. 连续控制19、惯性环节使系统的输出随输入信号的频率增加而其()。
D. 相位滞后20、相位裕量是衡量系统相对稳定性的指标。
只有()时,才能判断系统是稳定的。
B.二、多选(共计25分,每题2.5分,每题答案完全一样得满分,少选、多选、错选均不得分。
)21、增大欠阻尼二阶系统的无阻尼自由振荡频率,能够()。
B. 减少过渡过程时间22、某控制系统的开环传递函数为,以下描述正确的是()。
《自动控制理论(新)》武汉理工大学 期末在线考试答案

《自动控制理论(新)》武汉理工大学期末在线考试答案一、计算( 每题参考分值5分)1、已知某单位反馈系统的开环传递函数为: 1、绘制该系统以根轨迹增益Kr为变量的根轨迹(求出:渐近线、分离点、与虚轴的交点等);2、确定使系统满足的开环增益的取值范围。
正确答案:1、绘制根轨迹(1)系统有有3个开环极点(起点):0、-3、-3,无开环零点(有限终点);(2)实轴上的轨迹:(-∞,-3)及(-3,0);(3) 3条渐近线: (4) 分离点:得: (5)与虚轴交点:绘制根轨迹如右图所示。
2、开环增益K与根轨迹增益Kr的关系:得系统稳定时根轨迹增益Kr的取值范围:,系统稳定且为欠阻尼状态时根轨迹增益Kr的取值范围:,系统稳定且为欠阻尼状态时开环增益K的取值范围:2、系统结构图如下图所示:(1)写出闭环传递函数表达式;(2)要使系统满足条件:,,试确定相应的参数和;(3)求此时系统的动态性能指标;(4)时,求系统由产生的稳态误差;正确答案:解:(1)(2)(3)(4)(5)令:得:3、某系统的框图如下图所示,(1)设,要求系统在的作用下,超调量,调节时间秒,(按计算),求和;(2)当时,为使系统输出不受的影响,求顺馈环节的传递函数。
正确答案:解:(1)则,系统输出只受输入信号的影响,系统闭环传递函数可写成:由;可以计算出:;;因此系统的参数可由下式计算:(2)当时,从到的前向通道有两条:;;回路有:;;前向通道和回路互不接触,因此有:为使不受的影响,顺馈环节的传递函数应该满足:4、写出图2所示系统的传递函数。
正确答案:解:传递函数G(s):根据梅逊公式4条回路:, ,;无互不接触回路。
特征式:2条前向通道: ;5、设一单位反馈系统对数幅频特性如图所示(最小相位系统)。
(1)写出系统的开环传递函数(2)判别系统的稳定性(3)如果系统是稳定的,则求时的稳态误差。
正确答案:解:(1)系统的开环传函(2)由于是最小相位系统,所以可以通过计算相位裕量γ是否大于零来判断系统的稳定性。
2014年武汉理工大学控制工程考研复试试题(回忆版)

2014年武汉理工大学控制工程考研复试试题(回忆版)各位学弟学妹们回馈论坛我是14考武理机电学院学硕的一名考生初试380+ 考的专业课是机械原理139武汉理工学硕今年65个复试录取63个,只刷了两个人。
初试今年机械原理考的比较基础,有20个填空题,剩下的是简答题和计算题。
机械原理初试就用孙恒的《机械原理》第七版。
初试大题:1,自由度有一大题不难2,六杆机构,求速度用瞬心法做3,今年没有求自锁条件,就是把力画出来4,设计六杆机构大概就是曲柄摇杆+曲柄滑块常规题角度题设置的不好线几乎重合了。
5,凸轮今年凸轮是是偏心滚子凸轮然后让你画各种线,给的凸轮太小的画到最后线都分不清了,这题有点麻烦。
6,齿轮画图题常规题7,轮系常规题8,平衡题忘了考没加上填空简答大概就是10个大题复试:笔试:机械原理1,轮系判断是何种轮系不用算传动比2,一四杆机构求该四杆机构是曲柄摇杆机构条件3,什么是凸轮压力角,压力角大对凸轮传动有什么影响机械设计4,一对齿轮45号钢一个调质一个正火,问是否合理,为什么?该齿轮有什么原则设计?为什么?5,轴上零件的轴向固定和周向固定各有哪些方法?分别用在什么场合?控制工程6,稳定性的定义,和充分必要条件7,什么是控制系统?开环和闭环控制系统的区别8,给一个开环传递函数(含字母a)求系统稳定时a的取值范围?用劳斯判据机械制造技术基础9,名词解释机械加工工艺系统(3分)切削力(2分)定位(3分)4个还有一个忘了10,判断题(机械设计制造的,5个,每个2分)11,选择题(机械设计制造的,5个,每个2分)总体不难监考老师说不会写也要写满不然老师没法给分你懂得。
面试:一共4组学硕两组专硕两组我分在面试2组学硕和专硕面试二组的老师都坑爹一直问专业课问题准备的问题一个没问到学硕和专硕的一组听说老师都很和蔼,不问什么专业课问题,就是聊聊天。
最后其实考武汉理工初试很重要,复试基本是过程,今年学硕刷两个,专硕刷20个左右,专硕初试后10名貌似就只有1个上了(听说的)还有就是今年武汉理工生源好扩招了两次。
武汉理工大学 施工技术(新)答案

施工技术(新) 答案一、单选(共计100分,每题2.5分)1、Ⅰ级钢筋端部设180°弯钩,弯钩增长值为()。
(第五章知识点1钢筋的分类)A. 6.25dB. 3dC. 7.25dD. 5d答案:【A】2、轻型井点的井点孔口到地面以下0.5~1.0m的深度范围内,使用粘土填塞的主要目的是:()。
(第二章知识点8井点降水)A. 防止空壁坍塌B. 防止发生流砂现象C. 固定井点管D. 防止漏气和地表水下渗答案:【D】3、预应力钢筋张拉程序中的持荷2min的作用是()。
(第八章知识点2先张法)A. 降低钢筋的塑性变形B. 提高钢筋的强度C. 减少钢筋预应力损失D. 保证张拉施工安全答案:【C】4、当用单斗挖掘机开挖基槽时,宜采用的工作装置为()。
(第二章知识点10土方工程机械化施工)A. 正铲B. 反铲C. 拉铲D. 抓铲答案:【B】5、砌筑砖墙要有一定的组砌方式,是因为()。
(第四章知识点10砖砌体施工)A. 减少砍砖次数B. 保证墙面美观C. 保证墙体的整体稳定D. 施工方便答案:【C】6、履带式起重机起重杆的仰角α变大时()。
(第九章知识点2自行式起重机)A. Q变大B. Q变小C. R变大D. Q不变答案:【A】7、锚固钢绞线的较为可靠的锚具应为()。
(第八章知识点12预应力筋、锚具和张拉机具)A. DM5型镦头锚具B. JM12型夹片锚具C. XM型多孔夹片锚具D. 挤压锚具答案:【C】8、某构件采用机械张拉后张法施工,孔道长度为29.8m,预应力筋为单根粗钢筋,每根长8米,两端均用螺丝端杆锚具,则对焊接头数量为()个。
(第八章知识点11后张法)A. 3B. 4C. 5D. 6答案:【C】9、有6根直径为12mm的冷拉光圆钢筋组成的预应力钢筋束应用()。
(第八章知识点13钢筋束、钢绞线)A. 螺丝端杆锚具B. 绑条锚具C. 镦头锚具D. JM12-6锚具答案:【D】10、斜槎长度不得小于其高度的()。
武汉理工大学《自动控制原理》考试复习重点知识汇总

c(t) = −te−t − e−t + 1(t) = 1(t) − (1 + t)e−t t > 0
7,在本课程中引入拉氏变换不只是为了解微分方程,更重要的是通过它建立常参量线性系 统一种输入/输出描述的数学模型。
5
第二讲 系统的数学模型
2. 1. 基本要求 1.了解建立系统微分方程的一般方法,能对简单的机械网络和电路能列写出动态方程式。 2.掌握传递函数的概念及性质。 3.掌握典型环节的传递函数形式。 4.掌握由系统微分方程组建立动态结构图的方法。 5.掌握用动态结构图等效变换求传递函数和梅逊公式求传递函数的方法。 6.掌握系统的开环传递函数、闭环传递函数,对参考输入和对干扰的系统闭环传递函数及误 差传递函数的概念。
2. 2 重点讲解 1, 本章是建立常参量线性系统描述系统输入、输出关系的的两种数学模型:系统微分方程 式和传递函数,前者是时域描述,后者则是复数域的描述。建立系统的数学模型是一件非常 复杂的工作,它涉及对系统中每个部件的深入了解和专门的知识,这些都不是本课程可以解 决的问题。它要靠专业课学习和长期的工作实践的积累。这里只是介绍建立模型的一种思路 和原则步骤。
运用拉氏变换的线性性质和延迟定理,可得
L[
f
(t)]
=
L[t ⋅1(t)
− (t
− t0 ) ⋅1(t
− t0 ) − t0
⋅1(t
− t0 )]
=
1 s2
−
1 s2
e−t0s
−
t0 s
e−t0s
4,拉氏变换式的积分下限问题
拉氏变换的定义的积分下限为零,在工程实践中,应该有 0+ (零的右极限)和 0− (零的左
由式(1-1)直接可得( x = 0, y = 1, c = 2.55,θ = −78.7o )
武汉理工大学大学物理上-课后习题答案第5章课教材

教材习题解答5-1 一汽车发动机轼轴的转速度在12s 内由13min 102.1-⋅⨯r 均匀的增加到13min 107.2-⋅⨯r 。
求:①曲轴转动的角加速度;②在此时间内,曲轴转了多少圈?解 曲轴的初始角速度为123001026.160/102.122-⋅⨯=⨯⨯==s rad n ππω, ①曲轴做匀角加速度转动,其角速度t αωω+=0,所以曲轴转动的角加速度为()22201.13121026.11083.2-⋅=⨯-⨯=-=s rad t ωωβ②曲轴做匀角加速度转动,其转动的角位移为()20tωωθ+=∆()()rad 321045.22121026.183.2⨯=⨯⨯+=所以,在12s 内轼轴转过的圈数为()圈39021045.223=⨯=∆=ππθN5-2:质量为0.25kg 的物体,某一瞬时的位置矢量(2.0 2.0)m =-r i k ,此时它的速度-1(5.0 5.0)ms =-+V i k ,受到力 4.0F j =N 作用,那么(1)物体对原点的角动量是多少?(2)作用在物体上的力对原点的力矩是多少?解:这里质点的位置矢量r ,速度v 和力F 都表示为直角坐标的形式,因此用矢积的坐标表示法来给出角动量较为方便。
又(2.0 2.0)m =-r i k ,()-15.0 5.0ms =-+v i k ,0.25kg =m 及 4.0F j =N 。
根据L r p mr v =⨯=⨯ 有()()2-12-10.25 2.00.0 2.0kgm s 0.25 2.0 5.0 2.0 5.0kgm s 0 5.00.0 5.0=-=-⨯--⨯=⎡⎤⎣⎦-ij kLj 根据M r F =⨯有()0.0 2.0 2.00.02.00.0 2.0Nm Nm 8.08.0Nm 4.00.00.0 4.004.00⎛-⎫=-=+=- ⎪⎝⎭ij kM i k i k5-3:质量为2.0 kg 的质点,0t=时位于()0 4.0 2.0m =-r i j , 其速度为()2-16.0ms =-v t i ,求:(1)t 时刻质点对原点的角动量;(2)此时作用在质点上的力对原点的力矩解: (1)为了求出t 时刻质点的角动量,必须先得到t 时刻位置矢量的表示式,为此可以从速度的定义出发26.0dr v t i dt==-分离变量后积分()()()020336.04.0 2.0 2.04.0 2.0 2.0rtr dr t i dtr i j t i r t i j=---=-=--⎰⎰于是322-12.0[(4.0 2.0) 2.0](6.0)kgm s =⨯=--⨯-L r mv t i j t i 由于同方向矢量的矢积为零,且j i k ⨯=-,得22-124.0kgm s =-L t k (2)根据质点的角动量定理,有2(24.0)48.0dL d M t k tk dt dt==-=-Nm5-4 一质量为kg m 10.0=的小钢球接有一细绳,细绳穿过一水平放置的光滑钢板中部的小洞后挂上一质量为kg M 30.0=的法码,令钢球作匀速圆周运动,当圆周半径为m r 20.01=时砝码恰好处于平衡状态。
自控原理习题解答第五章

dk 3 2 4s 18s 20s 8 0 ds
s 1.5s 0.5 3 2 s 3 s 4.5s 5s 2
2
s 3s
3
2 2 2
1.5s 5s 1.5s 4.5s 0.5s 2 0.5s 1.5 0.5
s 0.5s 3 3 2 s 4 s 4.5s 5s 2
1
4 95.58
6求与虚轴的交点
s 1.1s 1.3s 0.5s k 0
4 3 2
s4 s3 s s
2
1 1.1 0.93 0.465 1.21k 1.1k
1.3 0.5 1.1k 0
k
s1
0
2 0.465 1.21k 0,0 k 0.38;0.93s 1.1k 0
4
j
45; l 1 : 3, 4 3 (135)
4
m i 1 i
a
p z
j1
nm
0.5 0.3 j0.96- 0.3 - j0.96- 0 0.275 4
4分离点 2 ss 0.5s 0.6s 1 k 0
试绘制系统的根轨迹图。
2实轴上的根轨迹: 0,0.5 3n m 4, 渐近线的倾角和渐近线 与实轴的交点 2l 1 , l 0,1,2
nm l 0 : 1, 2
n
k 答5 - 4Gs Hs ss 0.5 s 2 0.6s 1 1n 4, m 0, p1 0, p 2 -0.5, p 3 0.3 j0.96, p 4 0.3 j0.96
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题参考答案习题5-1 解:相角裕度可通过对数幅频特性用图解法求出。
K =10时, )/s )(s (s )s (G 511510++=图5-41 习题5-1解图由上图可知: 22020401lg K lg lgc==ωω 得剪切频率41412.c ==ω。
相角裕度为:︒=ω-ω-︒-︒=ωϕ+︒=γ519590180180.arctanarctan )(cc c 当K 从10变到100时,20lgK=20lg20=26dB ,如图中虚线所示。
202020401lg K lg lgc==ωω' 相角裕度为:︒-=ω'-ω'-︒-︒=ω'ϕ+︒=γ229590180180.arctanarctan )(cc c 求增益裕度,则需先求出g ω。
5180590=ω⇒︒-=ω-ω-︒-g g g arctanarctan当K=10时,有dB .lg)(A lg L ggg g g 54925110202022=ω+ω+ω-=ω-=当K=100时,有()dB A L ggg g g 5.10251100lg20lg 2022-=++-=-=ωωωω习题5-2 解:画出开环系统幅相频率特性,如下图所示:图5-42 习题5-2解图从上图中可知,1-=N ;而由表达式()()s H s G 可知0=P 。
根据Nyquist 判据有:()21202=-⨯-=-=N P Z ,因此闭环系统不稳定。
习题5-3 解: 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G习题5-4 解: 求系统闭环传递函数 5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义,以及线性系统的迭加性求解如下:(1)︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ(2)︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s(3))8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s习题5-5 解:系统闭环传递函数为Ks Ts Ks G s G s R s C s G K K B ++=+==2)(1)()()()( 10=ω时系统频率特性为 ())(10010tg 210210)(100)100(10100)()(1ωθωωωωωωj TK j e A eT K K j T K Kj T K K j G =+-=+-=+-=--==-由已知条件得2)(,1)(12πθθωθω-=-===r c A A A ,则有 ⎩⎨⎧==⇒⎪⎩⎪⎨⎧=-=+-1.01001001100)100(2T K T K T K K习题5-6 解:)116)(1()14(5)154)(1()(222++-+-=++=ωωωωωωωωωj K j j j Kj G0→ω时,︒-∞∠=→90)(lim 0ωωj G 。
求0→ω时的渐近线K K j G 5)116)(1(5lim)](Re[lim 2200-=++-=→→ωωωωωωω∞→ω时,︒-∠=∞→2700)(lim ωωj G ,曲线顺时针穿过负实轴求曲线与负实轴的交点 令0)](Im[=ωj G ,得5.0=ω。
K j G A g 25.11)](Re[)(5.0===ωωω 该系统幅相频率特性曲线如图所示。
当1)(=g A ω即25.1=K 时,闭环系统临界稳定。
习题5-7 解:(1)令 145tg 180180)(1801=⇒︒=+︒-︒=∠+︒=-c c c j G αωαωωγ由84.011)()(222=⇒=+==αωωαωωcc c c j G A(2)令1004501.0tg 3180)(1801=⇒︒=-︒=∠+︒=-c c c j G ωωωγ 由()()83.22111101.0)()(5.1332==⇒=+=⎪⎭⎫ ⎝⎛+==K KKj G A c c c ωωω(3)令10180100tg 90)(21=⇒︒-=--︒-=∠-g g gj G ωωωωdb j G K g 20)(lg 20=-=ω()101.0100100)(222=⇒==+-=⇒K KKj G g gg g ωωωω习题5-8 解:(1)51.03011.0tg 60tg 1.0tg 901802111≈⇒︒=-+⇒︒=--︒-︒=---c c cc c c ωωωωωωγ 57.0111)1.0(22=⇒=++K Kcc c ωωω(2)101801.0tg tg 90)(11=⇒︒-=--︒-=∠--g g g g j G ωωωω ()1.12011.01lg20)(lg 201022≈⇒=+⨯+⨯-=-==K Kj G K g g g g g g ωωωωω(3)︒≈⇒=≈58.454.1sin 1γγr M ︒=--︒-︒=58.45arctan 1.0arctan 90180c c ωωγ 83.0098.01.1098.042.44tan 1.011.022=⇒=-+⇒︒=-+c c c cc c ωωωωωω 1.11101.011101.083.02222=++==++=c c c c cccK Kωωωωωωω习题5-9 解:⎪⎪⎩⎪⎪⎨⎧≥≤=)1(lg 20)1(lg 20)(TT K TK L ωωωωωω constT T c c =-︒=-︒-︒=--ωωγ11tg 90tg 90180设穿越频率在T1≤ω频段,则K c =ω,若使c ω扩大a 倍,则K 扩大a 倍,且γ保持不变,显然T 需要缩小a 倍。
设穿越频率在T 1≥ω频段,则TK c =ω,若使c ω扩大a 倍,且同时保持γ不变,则T 应缩小a 倍,只有当K 扩大a 倍才能满足要求,即变化后的开环截止频率为c c a TK a a T aK ωω===' 两种情况的讨论结论一致,即K 扩大a 倍,T 缩小a 倍。
习题5-10 解: 计算相角裕量方法一,由对数幅频渐近线近似计算穿越频率c ω )505(07.712.010)50(02.02.010lg20)505(2.010lg 20)5(10lg 20)(≤≤==⨯⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧≥⨯⨯≤≤⨯≤=ωωωωωωωωωωωωωωc cc L相角裕量︒=--︒-︒=∠+︒=--22.2702.0tg 2.0tg 90180)(18011c c c k j G ωωωγ方法二,按定义计算穿越频率c ω22.611)02.0(1)2.0(1022≈⇒=++c c c c ωωωω相角裕量︒=--︒-︒=∠+︒=--7.3102.0tg 2.0tg 90180)(18011c c c k j G ωωωγ计算幅值裕量:令 s rad g g g 81.1518002.0tg 2.0tg 90)(11≈⇒︒-=--︒-=--ωωωωθ 方法一,由对数幅频渐近线近似得 得 )5081.155(dB142.010lg20)(1lg20≤=≤=⨯-==g gg g g j G k ωωωω方法二,由定义得dB 81.141)02.0(1)2.0(10lg20)(1lg2022=++-==g g g g g A k ωωωω∴ 系统闭环稳定。
习题5-11 解:① 典型环节的标准形式)11.0()102.0(50)(+-=s s s s G② 50=K ,0.34lg 20=K 。
③ 转折频率101=ω,一阶惯性环节;502=ω,不稳定的一阶微分环节。
④ 1=ν,低频渐近线斜率为dec dB 20-,且过(1,34dB )点。
⑤ 系统相频特性按下式计算ωωωθ02.0arctg 1801.0arctg 90)(-︒+-︒-=,得)/()(︒ωθ1105010011050100d B/)(ωL 2040349090-0ωω20-20-40-图5-43 习题5-11解图习题5-12 解:)116)(1()14(5)154)(1()(222++-+-=++=ωωωωωωωωωj K j j j Kj G0→ω时,︒-∞∠=→90)(lim 0ωωj G 。
求0→ω时的渐近线K K j G 5)116)(1(5lim)](Re[lim 2200-=++-=→→ωωωωωωω∞→ω时,︒-∠=∞→2700)(lim ωωj G ,曲线顺时针穿过负实轴。
求曲线与负实轴的交点 令0)](Im[=ωj G ,得5.0=ω。
K j G A g 25.11)](Re[)(5.0===ωωω该系统幅相频率特性曲线如下图所示。
图5-44 习题5-12解图当1)(=g A ω即25.1=K 时,闭环系统临界稳定。
习题5-13 解:[])1()1()1()1()1)(1()1)(1(1)1)(1()1(1)(31231212321311+++-+=-+-++-++=+=s T K s T s T s T K K s T s T s T s T K s T s T s T K K GH G K s G k二阶系统,有一个右半平面的开环极点,0,1==v p 。
由开环幅相曲线可知21,1==b a 。
0)11(21)(2=--=--=b a p z因此,系统稳定,复平面左半平面有两个闭环极点,右半平面、虚轴上均无闭环极点数。
习题5-14 解:时域分析法得特征方程为015001201.00)11.0(1201)11.0(305012322=+++⇒=+++⨯+s s s s s ss s1.01500120⨯< ,因此,该系统不稳定。
习题5-15 解:(1)网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R Cj R j G (2)绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j e T T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。
