水声定位算法学习总结培训课件
水声定位算法学习总结

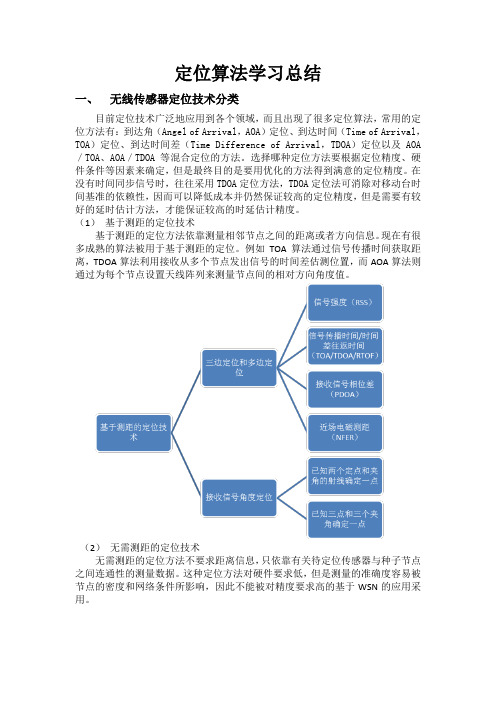
水声定位算法学习总结一、无线传感器定位技术分类目前定位技术广泛地应用到各个领域,而且出现了很多定位算法,常用的定位方法有:到达角(Angel of Arrival,AOA)定位、到达时间(Time of Arrival,TOA)定位、到达时间差(Time Difference of Arrival,TDOA)定位以及AOA/TOA、AOA/TDOA等混合定位的方法。
选择哪种定位方法要根据定位精度、硬件条件等因素来确定,但是最终目的是要用优化的方法得到满意的定位精度。
在没有时间同步信号时,往往采用TDOA定位方法,TDOA定位法可消除对移动台时间基准的依赖性,因而可以降低成本并仍然保证较高的定位精度,但是需要有较好的延时估计方法,才能保证较高的时延估计精度。
(1)基于测距的定位技术基于测距的定位方法依靠测量相邻节点之间的距离或者方向信息。
现在有很多成熟的算法被用于基于测距的定位。
例如TOA算法通过信号传播时间获取距离,TDOA算法利用接收从多个节点发出信号的时间差估测位置,而AOA算法则通过为每个节点设置天线阵列来测量节点间的相对方向角度值。
(2)无需测距的定位技术无需测距的定位方法不要求距离信息,只依靠有关待定位传感器与种子节点之间连通性的测量数据。
这种定位方法对硬件要求低,但是测量的准确度容易被节点的密度和网络条件所影响,因此不能被对精度要求高的基于WSN的应用采用。
二、三边定位和多变定位(1)信号强度(RSS,Received Signal Strength)通过信号在传播中的衰减来估计节点之间的距离,无线信道的数学模型PLd=PLd0-10nlogdd0-Xσ。
尽管这种方法易于实施,但却面临很多挑战。
首先信道由于受到信道噪声、多径衰减(Multi-path Fading)和非视距阻挡(Non-of- Sight Blockage)的影响[1],具有时变特性,严重偏离上诉模型;其次衰减率会随外界环境的不同而发生相应改变。
水声通信及海洋定位导航解决方案ppt

73%
项目一
20%
30%
ห้องสมุดไป่ตู้
项目二
56%
50%
项目三
29%
75% 项目四
77%
点击添加相关标题文字
ADD RELATED TITLE WORDS
在此输入关于此标题或图形的文字描述内容或者相关的数据。 在此输入关于此标题或图形的文字描述内容或者相关的数据。 在此输入关于此标题或图形的文字描述内容或者相关的数据。 在此输入关于此标题或图形的文字描述内容或者相关的数据。 在此输入关于此标题或图形的文字描述内容或者相关的数据。
01
PART 01
第一部分
项目简介
01 点击添加相关标题文字 03 点击添加相关标题文字
02 点击添加相关标题文字 04 点击添加相关标题文字
点击添加相关标题文字
ADD RELATED TITLE WORDS
标题文字
单击此处添加段落文本单击此 处添加段落文本
02
标题文字
单击此处添加段落文本单击此 处添加段落文本
2019
解决方案PPT
YEAR-END SUMMARY PLAN BUSINESS REPORT PPT IN THE NEW YEAR
Chinese companies will no longer remain in the hard stage and they are also promoting a culture Chinese companies will no longer remain
04
标题文字
单击此处添加段落文本单击此 处添加段落文本
05
01
标题文字
单击此处添加段落文本单击此 处添加段落文本
第4章_长基线水声定位系统(LBL)汇总

T2
t2
t1 2
F3 T1=t1/2
T2
F4
R2 c T2
应答器与TTS的距 离(多个)
8
2020/10/2
几种应用模式
舰船导航模式--简化模型
F3 R1i
F4
F3 F4
9
由于被定位目 标(水面船) 到应答器的单 程传播时间的 求解方法一样。 因此,可以简 化表示。
图中船上问答 机询问信号用 F3表示(通常 只有一个频 率),应答器 回答信号用F4 表示(实际上 有几个应答器 就有几个回答 频率)。
2020/10/2
几种应用模式
长基线有缆潜器(TTS)导航模式
母船上只有接收机,TTS上装有问答机。 定位对象为TTS 求TTS与T的斜距R2 工作过程
设:接收时刻t1、t2 单程传播时间T1、T2 则,
T2
1 2 t2
1 T1 t1 2 t2
问答机
t1 t2 T2
F3
R2 cT2 R1 cT1
4
换插图??
2020/10/2
引言
本章要解决的问题
本章主要研究利用海底应答器的长基线水声定位系统, 利用无线电浮标的长基线系统基本原理是相同的。
长基线系统的几种应用模式(定位解算时,依定位模 式的不同获取水声传播距离的方式也有所不同。)
海底应答器的标校(定位系统的阵元为应答器,因此 应答器的位置测量精度对定位精度有直接影响)
基线安装的位置:海底
特点:利用海底应
定位方法:长基线利用海底应答器阵来确定载体的位置 答器阵来确定载体
记录询问时刻和各应答器应答信号到达时刻
的位置----相对于
位置坐标:定位的坐标是海底应答器阵的相对坐标 海底应答器阵的相
水声学原理第五章ppt课件

College of Underwater Acoustic Engineering
HEU
3
0、第四章小结
射线声学 恒定声速梯度下声线水平传播距离求解 曲率半径和平面几何法 已知掠射角时的传播距离公式 已知深度时的传播距离公式 声线图绘制 聚焦因子物理意义
College of Underwater Acoustic Engineering
z0
15
二、表面声道
反转深度
概念:在表面声道中传播的声线发生反转的深度
反转深度处声线的特点:声线的掠射角为零
csc0 cH c
D
z0
z0
0 0
zm
z
College of Underwater Acoustic Engineering
HEU
16
二、表面声道
反转深度
cos 0
1 az0
1 1 azm
s
2
:海面处掠射角越大,跨度也越大
College of Underwater Acoustic Engineering
HEU
21
二、表面声道
跨度 最大跨度: 最小跨度:
Dmax
8H / a
D
2
sin s sin a coss
2 tan s
/a
Dmin 8z0 / a 海面处最大小掠射角:
本讲主要内容
第四章小结 邻近海面的水下点源声场 表面声道声线参数
College of Underwater Acoustic Engineering
HEU
1
0、第四章小结
定解条件 第一类齐次边界条件(绝对软) 第二类齐次边界条件(绝对硬) 边界上密度或声速的有限间断(压力和法向振速连续)
水声学原理第一章ppt课件

5
为了提高主动声纳的作用距离,将发射器做 成具有一定的发射指向性,如下图所示。
解释原因:可以提高辐射信号的强度,相应 也提高回声信号强度,增加接收信号的信噪 比,从而增加声纳的作用距离。
6
发射指向性指数DIT:
DI T
10 lg
ID I ND
式中:
ID为指向性发射器在声轴上测得的声强度; IND为无指向性发射器辐射的声强度。 含义:
的回波强度。
11
4、海洋环境噪声级NL (Noise Level)
Question:海洋内部是安静的吗?
海洋环境噪声是由海洋中大量的各种各样的噪声源发出的 声波构成的,它是声纳设备的一种背景干扰。
环境噪声级NL是度量环境噪声强弱的量
定义:
NL 10lg I N
I0
式中I0为参考声强度,IN是测量带宽内(或1Hz频带内)的
QUESTION:何为水听器灵敏度?
14
水听器灵敏度Sh
定义:
水听器处的声压为p,装置的开路终端电 压是V,则水听器的灵敏度为:
Sh 20 lg( v / p) dB/V
例子:已知水听器的灵敏度为-200dB/V,假设入 射平面波的声压级为80dB,问其输出端的开路电 压为几伏?
15
无指向性水听器产生的均方电压: 设水听器的灵敏度为单位值,噪声场为 各向同性的,单位立体角内的噪声功率 为Ii,无指向性水听器产生的均方电压 为:
目标反射本领有差异:在同样入射声波的照射下,不同 目标的回波是不一样的。它除了与入射声波特性(频率、 波阵面形状)有关,还与目标的特性(几何形状、材料 等)有关。 目标强度TS定量描述目标反射本领的大小
定义:
第4章长基线水声定位系统LBL

三个应答器的情况
用于4边形应答器阵的两种校准方法
1)条件方程法
2) 坐标变动法
16
2019/7/13
4.3 海底应答器阵的校准
两个应答器的情况
问答机
简单的方法是在应答器布
R1
放时利用无线电定位或
应答器1
GPS记下投放点的位置。
h
R2
应答器2
也可利用船上问答机与应 答器连续进行应答,测量 问答机与两应答器的距离。
20
2019/7/13
4.3 海底应答器阵的校准
四个应答器的情况 1)条件方程法
D
A6 A7
C
A5 A4
四边形的构成条件:
X
A8
四边形角度调整步骤为:
A1
8
A
由 Ai 360 式调整8个角度之和为0;
A3
A2 B
i 1
由式 A1 A2 A5 A6 0 和 A3 A4 A7 A8 0
应答信号
t3 2T1
问答机在t1时刻接收 到FSS发出来的信号
T1 F4
T5 t1
F2
F3
T3 F3
间隔 t3
T3 t2 t3 T1
15
R3 cT3
2019/7/13
4.3 海底应答器阵的校准
校准的目的:布放应答器时有误差≠GPS的数据。
本节提到的校准方法,即测量应答器的相对坐标,可以没有 GPS数据,在有GPS数据后可以得到应答器的绝对坐标,还 使校准方法简单化,可以绕着应答器航行,可以利用超短基线 +GPS初步确定应答器的位置,在通过解斜距方程,精确确 定应答器的位置。
水下定位与导航技术声学多普勒测速技术概述课件

24
2023/9/20
安装角度偏离误差及其校正 基阵安装误差带来的系统误差,可通过现场测速进 行校正。 由几何关系有两个速度之间的关系
安装角度与船的首尾线的几何关系
由多普勒测速仪可以得到的速度值为
25
2023/9/20
安装角度偏离误差及其校正
校准方法
安装偏移角的校正,可在海上进行。 船保持直线航行一段距离,例如几海里,在航速达到稳定
后利用差分GPS测量起止点的船位,根据航行时间得到船
的平均速度 vx、vy。
利用船上的高精度罗径得到的航向,算得船坐标系的两个
速度分量vx、vy 。在速度稳定航段中,利用多普勒计程仪 测得的两个速度分量同样也取平均值v’x、v’y.
计算安装偏移角
26
2023/9/20
安装角度偏离误差及其校正 校准方法
19
2023/9/20
5.3 影响多普勒测速的主要因素及改 进方法
由解算公式近似引起的误差 船舶摇摆引起的测速误差及摇摆补偿 传播声速引起的测速误差 有限波束宽度的影响 噪声对频率测量的影响 安装角度偏离误差及其校正
20
2023/9/20
噪声对频率测量的影响 过零检测法—测量N次过零的时间计算回波频率。
由公式可以看出,声速有多大的相对误差,将引起同样的测速 误差(相对误差)
进行声速补偿的方法
测量换能器表面处的声速,计算速度时使用现场测得的声速。
导流 测量换能器表明的温度,计算速度时使用现场测得的声速。
罩充 是利用专门的测量装置,测量温度、盐度和压力,再利用声速计
油,
算公式计算声速。
恒温
由声速的计算公式,只要保持
6
2023/9/20
水声定位算法学习总结
定位算法学习总结一、无线传感器定位技术分类目前定位技术广泛地应用到各个领域,而且出现了很多定位算法,常用的定位方法有:到达角(Angel of Arrival,AOA)定位、到达时间(Time of Arrival,TOA)定位、到达时间差(Time Difference of Arrival,TDOA)定位以及AOA /TOA、AOA/TDOA等混合定位的方法。
选择哪种定位方法要根据定位精度、硬件条件等因素来确定,但是最终目的是要用优化的方法得到满意的定位精度。
在没有时间同步信号时,往往采用TDOA定位方法,TDOA定位法可消除对移动台时间基准的依赖性,因而可以降低成本并仍然保证较高的定位精度,但是需要有较好的延时估计方法,才能保证较高的时延估计精度。
(1)基于测距的定位技术基于测距的定位方法依靠测量相邻节点之间的距离或者方向信息。
现在有很多成熟的算法被用于基于测距的定位。
例如TOA算法通过信号传播时间获取距离,TDOA算法利用接收从多个节点发出信号的时间差估测位置,而AOA算法则通过为每个节点设置天线阵列来测量节点间的相对方向角度值。
(2)无需测距的定位技术无需测距的定位方法不要求距离信息,只依靠有关待定位传感器与种子节点之间连通性的测量数据。
这种定位方法对硬件要求低,但是测量的准确度容易被节点的密度和网络条件所影响,因此不能被对精度要求高的基于WSN的应用采用。
二、三边定位和多变定位(1)信号强度(RSS,Received Signal Strength)通过信号在传播中的衰减来估计节点之间的距离,无线信道的数学模型。
尽管这种方法易于实施,但却面临很多挑战。
首先信道由于受到信道噪声、多径衰减(Multi-path Fading)和非视距阻挡(Non-of- Sight Blockage)的影响[1],具有时变特性,严重偏离上诉模型;其次衰减率会随外界环境的不同而发生相应改变。
根据接收到的信号估计出的距离d 将有很大误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定位算法学习总结一、无线传感器定位技术分类目前定位技术广泛地应用到各个领域,而且出现了很多定位算法,常用的定位方法有:到达角(Angel of Arrival,AOA)定位、到达时间(Time of Arrival,TOA)定位、到达时间差(Time Difference of Arrival,TDOA)定位以及AOA /TOA、AOA/TDOA等混合定位的方法。
选择哪种定位方法要根据定位精度、硬件条件等因素来确定,但是最终目的是要用优化的方法得到满意的定位精度。
在没有时间同步信号时,往往采用TDOA定位方法,TDOA定位法可消除对移动台时间基准的依赖性,因而可以降低成本并仍然保证较高的定位精度,但是需要有较好的延时估计方法,才能保证较高的时延估计精度。
(1)基于测距的定位技术基于测距的定位方法依靠测量相邻节点之间的距离或者方向信息。
现在有很多成熟的算法被用于基于测距的定位。
例如TOA算法通过信号传播时间获取距离,TDOA算法利用接收从多个节点发出信号的时间差估测位置,而AOA算法则通过为每个节点设置天线阵列来测量节点间的相对方向角度值。
(2)无需测距的定位技术无需测距的定位方法不要求距离信息,只依靠有关待定位传感器与种子节点之间连通性的测量数据。
这种定位方法对硬件要求低,但是测量的准确度容易被节点的密度和网络条件所影响,因此不能被对精度要求高的基于WSN的应用采用。
二、三边定位和多变定位(1)信号强度(RSS,Received Signal Strength)通过信号在传播中的衰减来估计节点之间的距离,无线信道的数学模型。
尽管这种方法易于实施,但却面临很多挑战。
首先信道由于受到信道噪声、多径衰减(Multi-path Fading)和非视距阻挡(Non-of- Sight Blockage)的影响[1],具有时变特性,严重偏离上诉模型;其次衰减率会随外界环境的不同而发生相应改变。
根据接收到的信号估计出的距离d将有很大误差。
(2)信号传播时间/时间差往返时间(TOA/TDOA/RTOF)a)到达时间(TOA,Time Of Arrival)使用发射机到接收机之间往返的时间来计算收发机之间的距离,要求发射机和接收机严格时间同步。
b)往返传播时间(RTOF,Roundtrip-Time-Of-Flight)发射机和接收机可属于不同的时钟域,基于信号传播时间的测距精度由时间差的测量精度决定。
时间差的精度由参考时钟决定。
c)到达时间差(TDOA,Time Difference Of Arrival)使用两种不同传播速度的信号,向同一个方向发送即可。
图1 示意图(3)接收信号相位差(PDOA,phase difference of Arrival)通过测量相位差,求出信号往返的传播时间[2],计算出往返距离,其中,是信号频率,是信号的波长,是发送信号和反射信号的相位差,由上式可知d的范围是[0,]。
不同的距离如果相差倍,则测量获得的相位相同。
通过相位差的方式测量距离,需要知道距离d范围,才能够确定出n的值,估算出距离。
(4)近场电磁测距(NFER,Near Field EM Ranging)利用近场与磁场的相位差来测量距离,射频信号包括电场和磁场两部分。
例如,当目标距离接近发射天线时相位相差90o;在距离相差1/2波长时,相位差接近0。
由此可以通过电场与磁场的相位差,估计到天线的距离。
近场电磁测距方法的测距范围在0.05之间,最佳测量范围0.08之间。
该方法由于距离限制,现有的定位系统很少采用。
三、TDOA算法研究1.算法种类RSS TOA RTOF TDOA PDOA NFER条件需求信号衰减量发射和接收机之间的往返时间往返传播时间目标发射信号到达各个节点的时间差接收信号相位差相位差与距离的准确关系优点易于实施,对硬件要求较低发射机和接收机可属于不同的时钟域对待测节点没有时间同步要求缺点算法模型受环境影响大,精度较低要求发射机和接收机严格时间同步使用射频信号时要求高精度时钟需要首先知道往返距离范围对测量距离有限制2.(1)对目标时间基准无依赖性选用TDOA算法对待测节点没有时间同步要求。
在无线传感器网络中,实现节点之间的时间同步较为困难。
而且考虑在实际应用中,一般情况下,我们无法获取待测目标的准确时间信息。
TDOA算法只需获取目标发射信号到达各个节点的时间差。
根据一个时间差信息即可将目标定位在一个双曲面上(如图3所示),那么假如有三个时间差信息,则三个双曲面可交与一点,这一点即为目标位置。
由此消除了对目标时间基准的依赖性[3],应用场合得以拓展。
图3 TDOA双曲面模型(2)适合水下环境要求对于水声定位系统,如果采用电磁波传递信息,则在水下将很快衰减。
因此只能够使用声波进行通信。
由上述分析可知,TDOA算法必须依靠高精度的参考时钟来保证其精确度。
对于低成本、低带宽、无参考时钟的无线传感器网络来说,获得高精度的时钟本身就是一个挑战。
如果用射频信号进行测距,的时钟精度就有300m的误差。
但使用超声波等低传播速率信号进行测距时,1ms的时钟精度便可达到30cm的精度。
可见,用超声波信号实现的TDOA算法不仅可满足水下环境的要求,而且能保证足够的定位精度。
3.TDOA算法分析在对目标信源进行定位时,因为无法获得时间同步信号而没有时间基准,常采用TDOA技术得到时延估计值,进而得到目标信源到两个基站之间的距离差,多个TDOA测量值就可以构成一组关于目标信源位置的双曲线方程组,求解该方程组就可以得到目标信源的估计位置[4]。
图4 TDOA算法模型设目标节点的坐标E为E=(x,y,z),其余N+1个已知位置的节点为P0, P1, ...,P m , ..., PN,它们的坐标分别为Pm= (xm, ym, zm),0 ≤ m ≤ N。
则目标与任一节点的距离为(1)为了简化计算可设主节点的坐标为(0,0,0),那么为(2)距离是水中声速v与传播时间的乘积,TDOA算法需要波面到达每个副节点P 1, ..., Pm, ..., PN与到达主节点P的时间差值,即v=v-v(3)v=-(4)图5为了更好地说明这一过程,如图5所示。
P0和P1分别是节点P0, P1接收到E的发射波形,可见P1接收到信号要比P延迟5ms左右,相当于的值。
对P0和P1的波形求互相关函数可得cross-correlation 波形。
其峰值时刻对应的时间值即为时间差。
上述仿真分析针对的是连续时间信号,对于离散时间信号可根据式(f*g)[n]进行计算。
1)非线性定位算法通过以上分析知要得到目标的坐标值,至少需要三个时间差信息,因此至少需要P0, P1, P2, P3四个已知位置的节点[5]。
设目标到达主站P0(0,0,0)与各副站的距离差为,则化简可得(5)(6)其中:,。
对于3个距离差测量值可以组成如下非线性方程组(7)先把r作为常量,求出x,y,z关于r的代数式,然后代入中解出r的值。
r的值确定后,x、y、z的值便可确定。
由整个计算过程可知这种非线性算法得到的解可能不唯一,需要解模糊。
此外计算量过大也是其缺点之一。
针对上述非线性算法存在的问题,我们在设计中采用基于最小二乘法的牛顿迭代定位算法对数据进行处理。
最小二乘法定位精度不是很高,但可对目标信源的位置作初始估计。
有了这一估计值,再使用牛顿迭代法对初始结果进行修正,则不但可以提高定位精度,而且可以加快计算速度,节省时间。
①最小二乘法估计初始位置由(8)可得矩阵形式的线性方程组HX=L (8)其中H=,X=,L=要求解X,必须使残差r=HX—L的平方和最小,即f(x)= (9)对上面的方程求导并令其为零,得(10)若为非奇异阵,则得到(11)的最小二乘法估计为(11)②牛顿迭代法修正(1)将用最小二乘法解得的信源位置X设为初始值,代入牛顿迭代法的关系式[3],求解迭代后的位置为(k=0,1,2,…,n-1);(2)分别将和代入n-4个冗余函数表达式(i=5,…,n),利用最优化方法,(i=5,…,n),为根据测距精度要求给定的值,,为给定的精度要求;(3)判断是否满足条件或,如果满足其中的一个条件,则迭代过程结束,输出,否则将结果作为初始值,即,继续上面的步骤,直到满足条件为止。
2)线性定位算法以上的非线性算法采用一个主节点和三个副节点,可测得三个时间差信息,即三个方程。
虽然这样可用最少的节点数目完成定位任务,节约成本,但是有着需解模糊、计算量大、定位实时性较低等缺点。
此时如果增加一个副节点P,则4线性方程组变为(12)此时可把r作为求解变量,直接求解四元一次线性方程组。
由(13)可得矩阵形式的线性方程组HX=L (13)其中H=,X=,L=可得X=H\L,由此可得出目标信源的位置。
由求解过程可以看出,线性定位算法相比非线性算法解法简单,无模糊,求解精度高。
该方法就是常用的五元十字TDOA定位算法。
4.仿真与分析基于上述算法分析,我们对基于最小二乘法的牛顿迭代算法和五元十字定位算法进行了Matlab仿真实验。
4.1 仿真实验(1)基于最小二乘法的牛顿迭代算法图6仿真实验传感器布阵图如图6所示,主节点坐标为=[0,0,0],三个副节点坐标分别为=[2,0,1]、=[0,2,0]、=[2,2,0]。
假设待测目标S的位置是S=[3,4,5]。
计算可得H=,L=最小二乘法估计= ,可见最小二乘法的估计值与目标的实际位置相差较大。
但通过牛顿迭代可提高精确度。
下面给出牛顿迭代法的部分Matlab代码:%牛顿迭代法解非线性方程组%输入参数:迭代初值,迭代方程,精度要求function [h]=Newton(start_newton,F_newton,p_newton)F_temp=start_newton;temp=[0;0;0];while sum(abs(temp-F_temp))>p_newtontemp=F_temp;F_temp=F_temp-subs(F_newton,{'x','y','z'},{F_temp(1),F_temp(2),F_ temp(3)});endh=F_temp;将最小二乘法的估计值代入,通过迭代后可得最终定位结果S’=[2.9998,3.9998,4.9997],S与S’的误差间距为3.9123e-004。
(2)五元十字定位算法图7 仿真实验传感器布阵图如图7所示,主节点坐标为=[0,0,0],四个副节点坐标分别为=[0,2,1]、=[-2,0,0]、=[0,-2,0]、=[2,0,0]。
仍假设待测目标S的位置是S=[3,4,5]。
计算可得H=,L=所以X=H\L=,可得最终定位结果S’=[2.9997,3.9993,4.9999],计算可得S与S’的误差间距为7.6811e-004。
