八年级数学(下册)矩形1PPT课件
合集下载
浙教版数学八年级下册 5.1 矩形 说课课件(共35张PPT)

教学问题 诊断分析
教学技术 支持条件
【设计意图】数学的学习不应该是单方面的教师授课制度,应该是学生在自 己的操作、实验、合作中完成的更有意义,因此这部分更加强调的是对一个 新的性质探索的路径,学生于此充分的感受活动,独立思考和小组配合以诞 生猜想和结论。
05
教学内容
教学目标
教学问题
教学技术
及其解析
教学问题 诊断分析
教学技术 支持条件
【设计意图】首先让学生描述一下生活中能够抽象到的矩形,注重对学生用 数学眼光观察现实世界的培养。再类比已学的几何图形研究视角,归纳几何 图形探究的视角可以从边,角,特殊的线和对称性进行研究,从而让矩形学 习的发生更加自然。
05
教学内容
及其解析
架构体系,启航
教学目标 及其解析
03
教学内容
教学目标
及其解析
及其解析
教学技术 支持条件
教学过程 及其设计
(1)具备的基础(知识、能力) 在知识层面上,八年级的下册学生已经经历第四章平行四边形的推理过程, 也感受过从普通四边形特殊化到平行四边形的过程,本章作为特殊平行四 边形的起始课,学生初步能用特殊化角的视角进行展开;从情感角度看, 作为此阶段的学生,基本的推理能力已经具备,也懂得一定自我探索和总 结的方法,因此需要将过程更多的交给学生.
05
教学内容
及其解析
概念生成,源起
教学目标 及其解析
教学问题 诊断分析
教学技术 支持条件
【设计意图】架设平行四边形的一种特殊化视角,介绍概念,通过定义强调 出矩形和平行四边形的包含关系,作为新概念课程,书写方式的规范性和几 何语言的表达也需要一定强调。
05
教学内容
华东师大版数学八年级下册1矩形19. 矩形的判定课件

3.如图,在▱ABCD中,点M为CD边的中点,且AM=BM.求证:四边形ABCD是矩 形.
易证△AMD≌△BMC(SSS),∴∠C=∠D.又∵∠C+∠D=180°,∴∠C=∠D= 90°,∴四边形ABCD是矩形
知识点❷:矩形的判定定理1——有三个角是直角的四边形是矩形 4.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合 作学习小组的4位同学拟定的方案,其中正确的是( D ) A.测量对角线是否相互平分 B.测量两组对边是否分别相等 C.测量一组对角是否都为直角 D.测量四边形其中的三个角是否都为直角
11.(安顺中考)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜
边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连结MN,则线 段MN的最小值为__15_2_.
12.(202X·连云港)如图,点C是BE的中点,四边形ABCD是平行四边形. (1)求证:四边形ACED是平行四边形; (2)如果AB=AE,求证:四边形ACED是矩形. 证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中 点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形 (2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形 ACED是平行四边形,∴四边形ACED是矩形
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
19.1 矩形19.1.2 矩形的判定
知识点❶:有一个角是直角的平行四边形是矩形 1.如图,要使▱ABCD成为矩形,需添加的条件是( B ) A.AB=BC B.∠ABC=90° C.∠1=∠2 D.AC⊥BD
2.如图,在△ABC中,AD⊥BC于点D,DE∥AC交AB于点E,DF∥AB交AC于点F, 连结DE,FD,当△ABC满足条件____∠__B__A_C_=__9_0时°,四边形AEDF是矩形.
人教版初中八年级下册数学课件 《矩形》平行四边形(第1课时矩形的性质)

A
D
O
B
C
基础训练 1. 下面性质中,矩形不一定具有的是( D)
A.对角线相等
B.四个角都相等
C.是轴对称图形 D.对角线垂直
2. 过四边形的各个顶点分别作对角线的平行线,若这四条平行 线围成一个矩形,则原四边形一定是( D )
A.对角线相等的四边形 B.对角线互相平分且相等的四边形 C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3.如图,在Rt△ABC中,∠ACB=90°,∠A=30°.点D是 AB的中点,点E为边AC上一点,连接CD,DE,以DE为边在 DE的左侧作等边△DEF,连接BF. 判断△BCD的形状;
温馨提示:矩形的定义有两个要素:
A
D
①四边形是平行四边形
②有一个角是直角,二者缺一不可。
B
C
矩形是特殊的平行四边形,因此它具有平行四边形的所有性质, 但它也有自己独特的性质。
2.矩形的性质(从边、角、对角线三个方面总结)
(1).边:①两组对边分别平行 ② 两组对边分别相等
A
D
几何语言:∵四边形ABCD是矩形
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对 角线所夹锐角的度数为( )D
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于
()
A
A.30° B.45° C.60° D.120°
例2. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小 三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
B
C
∴AB//CD,AD//BC
AB=CD,AD=BC
八年级数学下册-矩形的判定-ppt课件新人教版
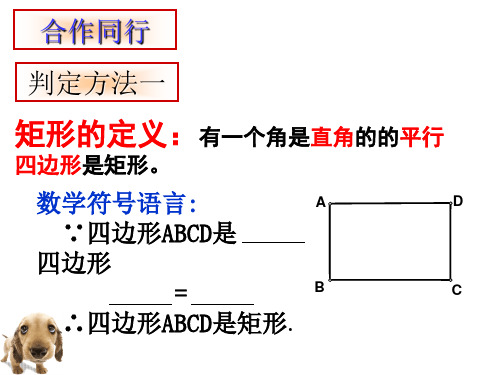
随堂练习
p 136(1)(2)
1、下面说法中正确的是 ( D )
A 有一个角是直角的四边形是矩形 B 两条对角线相等的四边形是矩形 C 两条对角线互相垂直的四边形是矩形 D 四个角都是直角的四边形是矩形
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
生活中的数学
给你一根足够长的绳子,你能检查教 室的门窗或你的桌子是不是矩形吗?你 怎样检查?你现在能解释其中的道理吗?
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习 (1)已知:如图,在平行四边 形ABCD中,AC、BD 相交于点 O,△ AOB是等腰三角形。求: ∠BAD的度数
解:∵ △AOB是等腰三角形 ∴OA=OB
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2BO
A
∴AC=BD
∴平行四边形ABCD是矩形
∴∠BAD=90°
B
D O
C
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习
3、能够判断一个四边形是矩形的条件是(A)
A 对角线相等
【最新】人教版八年级数学下册第十八章《18.2.1 矩形(第1课时)》公开课课件.ppt

• 10、人的志向通常和他们的能力成正比例。2021/1/112021/1/112021/1/111/11/2021 6:23:00 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/1/112021/1/112021/1/11Jan-2111-Jan-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/1/112021/1/112021/1/11Monday, January 11, 2021 • 13、志不立,天下无可成之事。2021/1/112021/1/112021/1/112021/1/111/11/2021
A
DA
D
B
C
B
C
A
DA
D
B
C
B
C
定义:有一个角是直角的平行四边形叫做矩形.
四边形
平行四边形 矩形
探究:矩形具有哪些性质?
1. 矩形具有平行四边形的所有性质. 2. 矩形特有的性质: ① 矩形的Байду номын сангаас个角都是直角; ② 矩形的对角线相等. 3. 矩形的是对中称心性对:称图形,也是轴对称图形.
你在矩形中还发现了哪些基本图形?
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形 第1课时
知识回顾: 1. 平行四边形有哪些性质?
2. 我们都知道三角形具有稳定性, 平行四边形也具有稳定性吗?
D
C
D
C
D
C
A
B
A
B
A
B
3. 在推动平行四边形的过程中,什么发生 变化了?什么没变?
4. 在上述变化过程中,你有没有发现一种 熟悉的、更特殊的图形? 生活中有很多具有矩形形象的物品,你 能举出一些例子吗?
A
DA
D
B
C
B
C
A
DA
D
B
C
B
C
定义:有一个角是直角的平行四边形叫做矩形.
四边形
平行四边形 矩形
探究:矩形具有哪些性质?
1. 矩形具有平行四边形的所有性质. 2. 矩形特有的性质: ① 矩形的Байду номын сангаас个角都是直角; ② 矩形的对角线相等. 3. 矩形的是对中称心性对:称图形,也是轴对称图形.
你在矩形中还发现了哪些基本图形?
第十八章 平行四边形
18.2 特殊的平行四边形
18.2.1 矩形 第1课时
知识回顾: 1. 平行四边形有哪些性质?
2. 我们都知道三角形具有稳定性, 平行四边形也具有稳定性吗?
D
C
D
C
D
C
A
B
A
B
A
B
3. 在推动平行四边形的过程中,什么发生 变化了?什么没变?
4. 在上述变化过程中,你有没有发现一种 熟悉的、更特殊的图形? 生活中有很多具有矩形形象的物品,你 能举出一些例子吗?
18.2.1矩形(第一课时)课件人教版数学八年级下册

18.2.1 矩形(第一课时)
从一般到特殊
? ?
从一般到特殊
?
学习目标
1.理解矩形的概念,明确矩形与平行四边形的区别和联系. 2.探索并证明矩形的性质,会用矩形性质解决相关问题. 3.探索并掌握“直角三角形斜边上的中线等于斜边的一半” 这一重要结论.
一、提出问题,形成概念
问题1 请用6根火柴拼一个平行四边形.
CB的延长线于点E.求证:∠EAB=∠CAB .
A
D
证明:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
O
∴ OA=OB.
E
B
C
∴ ∠OAB=∠OBA.
∴ ∠EAB=∠OBA .
∵ AE∥BD,
∴ ∠EAB=∠CAB .
三、运用性质,解决问题
例2 如图,四边形ABCD是矩形,AE∥BD ,且交
B
C
证明:∵ 四边形ABCD是矩形,
∴ ∠B=90º,AD∥BC,∠A=∠C,∠B=∠D.
∴ ∠A=180º-∠B=90º.
∴ ∠C=∠A=90º,∠D=∠B=90º.
∴ ∠A=∠B=∠C=∠D=90º.
二、探究性质,深化认知 A
D
猜想2:矩形的对角线相等.
已知:四边形ABCD是矩形. 求证: AC=BD.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,
∠AOB =60°,AB=4,求矩形对角线的长.
A
D
O
B
C
三、运用性质,解决问题
例1 如图,矩形ABCD的对角线AC,BD相交于点O,
∠AOB =60°,AB=4,求矩形对角线的长.
解:∵ 四边形ABCD是矩形, A
从一般到特殊
? ?
从一般到特殊
?
学习目标
1.理解矩形的概念,明确矩形与平行四边形的区别和联系. 2.探索并证明矩形的性质,会用矩形性质解决相关问题. 3.探索并掌握“直角三角形斜边上的中线等于斜边的一半” 这一重要结论.
一、提出问题,形成概念
问题1 请用6根火柴拼一个平行四边形.
CB的延长线于点E.求证:∠EAB=∠CAB .
A
D
证明:∵ 四边形ABCD是矩形,
∴ AC与BD相等且互相平分.
O
∴ OA=OB.
E
B
C
∴ ∠OAB=∠OBA.
∴ ∠EAB=∠OBA .
∵ AE∥BD,
∴ ∠EAB=∠CAB .
三、运用性质,解决问题
例2 如图,四边形ABCD是矩形,AE∥BD ,且交
B
C
证明:∵ 四边形ABCD是矩形,
∴ ∠B=90º,AD∥BC,∠A=∠C,∠B=∠D.
∴ ∠A=180º-∠B=90º.
∴ ∠C=∠A=90º,∠D=∠B=90º.
∴ ∠A=∠B=∠C=∠D=90º.
二、探究性质,深化认知 A
D
猜想2:矩形的对角线相等.
已知:四边形ABCD是矩形. 求证: AC=BD.
例1 如图,矩形ABCD的对角线AC,BD相交于点O,
∠AOB =60°,AB=4,求矩形对角线的长.
A
D
O
B
C
三、运用性质,解决问题
例1 如图,矩形ABCD的对角线AC,BD相交于点O,
∠AOB =60°,AB=4,求矩形对角线的长.
解:∵ 四边形ABCD是矩形, A
八年级数学下册教学课件《矩形的判定》
H
(3)将直角尺靠窗框的一个角,如图③,调整窗框的边框,当直角尺的两
条直角边与窗框无缝隙时, 如图④, 说明窗框合格, 这时窗框是 矩形 ,
根据的数学道理是 有一个角是直角的平行四边形叫做矩形 .
概念可以判定矩形,比照平行四边形的判定,那矩形性质的逆命题是
不是也可以用于矩形的判定呢? 我们来看下.
探索新知
∴四边形 ABCD 是矩形
对应训练
如图,在△ABC中,∠ACB=90°,D是AB的中点,DF,
DE分别是△BDC,△ADC的角平分线. 求证:四边形DECF是
矩形. 证明:∵ ∠ACB=90°,D是AB的中点,
A
∴AD=CD=BD.
E
D
∵DE是△ADC的角平分线, ∴DE⊥AC.
∴∠DEC=90°. 同理得∠CFD=90°. C
D F
②
③
④
G
H
(1)先截出两对符合规格的铝合金窗料,如图①,使AB=CD , EF=GH ; (2)摆放成如图②所示的四边形,则这时窗框的形状是 平行四边形 , 根据的数学道理是 两组对边分别相等的四边形是平行四边形 ;
情境导入
工人师傅做铝合金窗框,分下面三个步骤进行:
A
B
①C E
D F
②
③
④
G
A
m
hm
Bn
nC
课后作业
解:能拼成三种平行四边形. (1)如图①的矩形,其对角线长为m. (2)如图②的平行四边形. 其两条对角线长分别为n, 4h2 n2 (3)如图③的平行四边形, 其对角线长分别为h, 4n2 h2
Байду номын сангаас
m n
h ① mn
华东师大版八年级下册数学1.1矩形的性质课件(1)
§19.1.1 矩形的性质
八年级 数学下册 (华师大版)
矩形的定义
有一个角是 直 角的平行四边形 叫做矩形.
A
D
∟
B
C
A
D
矩形的性质
O
B
C
对称性
边
角
对角线
平行四边形 是中心对称 对边平行 对角相等, 对角线互
的一般性质 图形
且相等 邻角互补
A
D
O
B
C
1、从对称性、边、角、对角线四个方面进 行考虑,你能发现矩形有什么特有的性质吗?
A
D
符号语言:
∵ 四边形ABCD是矩形
∴__A_C_=_B__D__
B
C
注:矩形的两条对角线把矩形分成了四个 等腰三角形和四个直角三角形.
A
D
矩形的性质
O
B
C
对称性
边
角
对角线
平行四边形 中心对称图 对边平行 对角相等, 对角线互
的一般性质 形
且相等
邻角互补 相平分
矩形的特殊 轴对称图形 邻边垂直 性质
分,则这个矩形的面积为
.
A
ED
∟
B
C
5、如图,矩形ABCD被两条对角线分成四个小
三角形,如果四个小三角形周长的和是86cm,
矩形的对角线长是13cm , 那么该矩形的周长
是
.
A
D
O
B
C
课堂小结
你有什么收获 或感想?你还 有什么疑问?
2、请以小组的情势讨论总结,并填写完整 前面的表格(课本99页).
矩形是轴对称图形,一共有两条对称轴.
A
D
∟
八年级 数学下册 (华师大版)
矩形的定义
有一个角是 直 角的平行四边形 叫做矩形.
A
D
∟
B
C
A
D
矩形的性质
O
B
C
对称性
边
角
对角线
平行四边形 是中心对称 对边平行 对角相等, 对角线互
的一般性质 图形
且相等 邻角互补
A
D
O
B
C
1、从对称性、边、角、对角线四个方面进 行考虑,你能发现矩形有什么特有的性质吗?
A
D
符号语言:
∵ 四边形ABCD是矩形
∴__A_C_=_B__D__
B
C
注:矩形的两条对角线把矩形分成了四个 等腰三角形和四个直角三角形.
A
D
矩形的性质
O
B
C
对称性
边
角
对角线
平行四边形 中心对称图 对边平行 对角相等, 对角线互
的一般性质 形
且相等
邻角互补 相平分
矩形的特殊 轴对称图形 邻边垂直 性质
分,则这个矩形的面积为
.
A
ED
∟
B
C
5、如图,矩形ABCD被两条对角线分成四个小
三角形,如果四个小三角形周长的和是86cm,
矩形的对角线长是13cm , 那么该矩形的周长
是
.
A
D
O
B
C
课堂小结
你有什么收获 或感想?你还 有什么疑问?
2、请以小组的情势讨论总结,并填写完整 前面的表格(课本99页).
矩形是轴对称图形,一共有两条对称轴.
A
D
∟
华东师大版八年级下册数学19.矩形的判定课件(1)
直线MN∥BC,设MN交∠BCA的平分线于点E, 交∠BCA的外角平分线于点F, (1)求证:OE=OF; (2)当点O运动到何处时,四边形AECF是矩形,并
证明你的结论。
布置作业
教材P106页 2题 107页3,5题
谢谢
A
D
分析:要证四边形 ACBD是矩形,已经 有一个直角的条件, 若能证它是平行四边 形就可以了。
C
E B
巩固练习1. 1.已知:如图, ABCD的四个内角的平分线分别相 交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:∵AB∥CD ∴∠ABC+∠BCD=180° ∵BG平分∠ABC,CG平分∠BCD
猜想:有三个角是直角的四边形是矩形
你能证明上述结论吗?
有三个角是直角的四边形是矩形。
A
D
B
C
已知:在四边形ABCD中,∠A= ∠B= ∠C=900。
求证:四边形ABCD是矩形。
情境二:木工师傅检查所做的门窗是否是 矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相
等来判断所做的门窗是否是矩形。因为对角 线相等的平行四边形是矩形。
证明: ∵ABCD是平行四边形 A
M
D
∴ AB∥CD AB=CD ∴ ∠A+ ∠D=1800
∵M是AD的中点 ∴AM=DM
∵ MB= M∴C△BAM≌ △CDM ∴∠A= ∠D
B
C
∴∠A= 900 ∴ ABCD是矩形
例2:延长Rt△ABC斜边上的中线CE到D, 使DE=CE。求证:四边形ACBD是矩形。
对角线相等的平行四边形是矩形。
A
D
B
C
已知:在 ABCD中,AC= BD。
证明你的结论。
布置作业
教材P106页 2题 107页3,5题
谢谢
A
D
分析:要证四边形 ACBD是矩形,已经 有一个直角的条件, 若能证它是平行四边 形就可以了。
C
E B
巩固练习1. 1.已知:如图, ABCD的四个内角的平分线分别相 交于E、F、G、H,求证:四边形 EFGH为矩形.
证明:∵AB∥CD ∴∠ABC+∠BCD=180° ∵BG平分∠ABC,CG平分∠BCD
猜想:有三个角是直角的四边形是矩形
你能证明上述结论吗?
有三个角是直角的四边形是矩形。
A
D
B
C
已知:在四边形ABCD中,∠A= ∠B= ∠C=900。
求证:四边形ABCD是矩形。
情境二:木工师傅检查所做的门窗是否是 矩形常用什么方法?为什么?
答:木工师傅靠测量门窗的对角线是否相
等来判断所做的门窗是否是矩形。因为对角 线相等的平行四边形是矩形。
证明: ∵ABCD是平行四边形 A
M
D
∴ AB∥CD AB=CD ∴ ∠A+ ∠D=1800
∵M是AD的中点 ∴AM=DM
∵ MB= M∴C△BAM≌ △CDM ∴∠A= ∠D
B
C
∴∠A= 900 ∴ ABCD是矩形
例2:延长Rt△ABC斜边上的中线CE到D, 使DE=CE。求证:四边形ACBD是矩形。
对角线相等的平行四边形是矩形。
A
D
B
C
已知:在 ABCD中,AC= BD。
人教版数学八年级下册《矩形(1)》课件
△
直角三角形
≌ △ ≌
勾股定理
△ ≌ △
4.如图,在矩形ABCD中,对角线AC,BD交于点O,
若∠COD=50°,那么∠CAD的度数是( B )
A.20°
B.25°
C.30°
D.40°
等腰三角形
△
≌ △
△
≌ △
应用新知
18.2.1矩形
第一课时
第十八章
平
行
四
边
形
作业
1.如图,在四边形ABCD中,对角线AC,BD相交于
点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
则四边形ABCD的面积为( D )
A.6
B.12
C.20
D.24
2.在▱ABCD中,E、F分别在BC、AD上,若想要使四边
形AFCE为平行四边形,需添加一个条件,这个条件不
可以是( B )
A.AF=CE
B.AE=CF
C.∠BAE=∠FCD
D.∠BEA=∠FCE
平行四边形
5
3
5
3
4
பைடு நூலகம்业
3.如图,在△ABC中,∠BAC=70°,∠ABC和∠ACB的角平分线
交于D点,E、F、G、H分别是线段AB、AC、BD、CD的中点.
求证:四边形EGHF为平行四边形.
证明:∵ 点、、、分别是、、、的中点
∴ = = = =
∵ =
=
∴ ∥ =
∵ = =
∴ ∥ =
∴ ∥ =
∴ 四边形是平行四边形
知识回顾
直角三角形
≌ △ ≌
勾股定理
△ ≌ △
4.如图,在矩形ABCD中,对角线AC,BD交于点O,
若∠COD=50°,那么∠CAD的度数是( B )
A.20°
B.25°
C.30°
D.40°
等腰三角形
△
≌ △
△
≌ △
应用新知
18.2.1矩形
第一课时
第十八章
平
行
四
边
形
作业
1.如图,在四边形ABCD中,对角线AC,BD相交于
点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
则四边形ABCD的面积为( D )
A.6
B.12
C.20
D.24
2.在▱ABCD中,E、F分别在BC、AD上,若想要使四边
形AFCE为平行四边形,需添加一个条件,这个条件不
可以是( B )
A.AF=CE
B.AE=CF
C.∠BAE=∠FCD
D.∠BEA=∠FCE
平行四边形
5
3
5
3
4
பைடு நூலகம்业
3.如图,在△ABC中,∠BAC=70°,∠ABC和∠ACB的角平分线
交于D点,E、F、G、H分别是线段AB、AC、BD、CD的中点.
求证:四边形EGHF为平行四边形.
证明:∵ 点、、、分别是、、、的中点
∴ = = = =
∵ =
=
∴ ∥ =
∵ = =
∴ ∥ =
∴ ∥ =
∴ 四边形是平行四边形
知识回顾
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类比思考 探究性质
为什么矩形的被子和床单可以反复折叠仍然是矩形? 请你用一张矩形纸片做模拟实验,并说明原因.
类比思考 探究性质
如图,一张矩形纸片,沿着对角线剪去一半,你能 得到什么结论?
A
D
A
O
B
C
O
B
C
Rt△ABC中,BO是一条怎样的线段?它的长度与斜 边AC有什么关系?一般地,这个结论对所有直角三角形 都成立吗?
A
D
O
B
C
运用性质 解决问题
例2(补充)已知:如图 ,矩形 ABCD, AB长8 cm ,对角线比AD边长 4 cm.求 AD的长及点A到BD的距离AE的长
运用性质 解决问题
例3(补充) 已知:如图,矩形ABCD中, E是BC上一点,DF⊥AE于F,若AE=BC. 求证:CE=EF.
课堂小结
矩形:有一个角是直角的平行四边形叫做矩形.
类比思考 探究性质
三位学生正在做投圈游戏,他们分别站在一个直角 三角形的三个顶点处,目标物放在斜边的中点处.三个 人的位置对每个人公平吗?请说明理由.
A
O
B
C
运用性质 解决问题
例1 如图,矩形ABCD的两条对角线相交于点O, 且∠AOB=60°,AB=4 cm.求矩形对角线的长.
你还能得出哪些结论?
You Know, The More Powerful You Will Be
谢谢你的到来
学习并没有结束,希望大家继续努力
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人:XXXXXX 时 间:XX年X; 矩形的四个角都是直角; 矩形的对角线相等且互相平分.
直角三角形斜边上的中线等于斜边的一半. 矩形是轴对称图形,连接对边中点的直线是它的两 条对称轴.
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
的平行四边形叫做矩
形. 小学中学习过的
长方形是矩形吗?正
DC
方形是矩形吗?
独木桥
类比思考 探究性质
作为特殊的平行四边形,矩形具有平行四边形所有 的性质.此外,矩形还有哪些一般平行四边形没有的特 殊性质呢?
A
D
A
D
B
OC
O
B
C
你能分别证明这些猜想吗? 矩形是轴对称图形吗?如果是,指出它的对称轴, 并用轴对称性质解析矩形的性质.
八年级 下册
18.2.1 矩形(1)
观察下列图片有何特征?
当平行四边形移动到一个角是直角时停止, 观察这是什么图形?
观察思考 形成概念
当独木桥前后运动时,四边形ABCD是什么形状? 当独木桥最后停下时,四边形ABCD有什么特殊的变化? 当独木桥静止时,四边形ABCD是什么图形?
有一个角是直角 A B
