磁悬浮球系统的自适应控制器设计
磁悬浮小球控制系统软件设计毕业设计(论文)

磁悬浮小球控制系统软件设计摘要磁悬浮技术具有无摩擦、无磨损、无需润滑以及寿命较长等一系列优点,在能源、交通、航空航天、机械工业和生命科学等高科技领域有着广泛的应用背景。
随着磁悬浮技术的广泛应用,对磁悬浮系统的控制已成为首要问题。
本设计以PID控制为原理,设计出PID控制器对磁悬浮系统进行控制。
在分析磁悬浮系统构成及工作原理的基础上,建立磁悬浮控制系统的数学模型,并以此为研究对象,设计了PID控制器,确定控制方案,运用MATLAB软件进行仿真,得出较好的控制参数,并对磁悬浮控制系统进行实时控制,验证控制参数。
最后,本设计对以后研究工作的重点进行了思考,提出了自己的见解。
PID控制器自产生以来,一直是工业生产过程中应用最广、也是最成熟的控制器。
目前大多数工业控制器都是PID控制器或其改进型。
尽管在控制领域,各种新型控制器不断涌现,但PID控制器还是以其结构简单、易实现、鲁棒性强等优点,处于主导地位。
关键字:磁悬浮系统,PID控制器,MATLAB仿真ABSTRACTMagnetic suspension technology, which has a series of advantages such as contact-free, no friction, no wear, no need of lubrication and long life expectancy, is widely concerned and adopted in high-tech areas such as energy, transportation, aerospace, industrial machinery and life science.With the extensive application of maglev technology, the control of the maglev system has become a priority. In this paper, for the principle of PID control, PID controller designed to control magnetic suspension system.On the basis of analyzing of magnetic suspension system’s structure and working principle, its system mathematical model was established, this thesis describe PID controller designed and get control scheme. It gets the better control parameters by MATLAB software simulation studies, and real-time control of magnetic suspension control system to verify the control parameters. The key research works for further study are proposed at last.Since PID controllers have been the process of industrial production has been most widely and most sophisticated controller. Most industrial controllers are PID controllers or modified. While in the control area, a variety of new controllers continue to emerge, but the PID controller is its simple structure, easy to implement, robust, etc., in a dominant position.Key words: magnetic suspension system; PID controller; MATLAB simulation毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
磁悬浮系统的控制器设计

第8卷 第3期2009年9月 太原师范学院学报(自然科学版)J OU RNAL OF TA IYUAN NORMAL UN IV ERSIT Y (Natural Science Edition ) Vol.8No.3 Sept.2009磁悬浮系统的控制器设计王华东 徐 军(江苏财经职业技术学院电子工程系,江苏淮安223001) 〔摘要〕 在建立磁悬浮系统微分方程模型基础上,引入状态变量将其线性化为状态空间模型.运用MA TL AB 软件计算其极点,并确定了PID 控制器的参数,最后对系统的脉冲响应进行了仿真.〔关键词〕 磁悬浮;MA TL AB ;PID 控制器;脉冲响应〔文章编号〕 167222027(2009)0320050204 〔中图分类号〕 TP27 〔文献标识码〕 A0 引言磁悬浮是利用电磁力使物体悬浮的现象.从磁场类型看,一种是交流磁悬浮,导体在交变磁场中产生涡流,涡流又产生磁场,两种磁场相互作用使导体悬浮.另一种是直流磁悬浮,悬浮的物体必须是铁磁性物体,靠电磁铁的吸引力使其悬浮.目前应用中的小型的磁悬浮设备有磁悬风扇和磁悬浮轴承等.磁悬浮风扇利用磁悬浮技术,使转子与定子之间保持不接触,因此磁悬浮风扇噪声小、震动小、寿命长.据相关资料介绍,一种新型的磁悬浮潜水电泵实现了推力轴承磁悬浮、无磨损,使机器使用时间成倍延长,省去了频繁的2000小时左右定期检修工作,可连续运转数万小时,节省了维修、检修费用,并且使潜水电泵的扬程有了突破性提高.图1 磁悬浮系统Fig.1 Magnetic levitation system本文主要研究直流磁悬浮设备的控制器的设计,目的是让悬浮的物体受到外界干扰时仍然回到原来的位置.本文不涉及悬浮物体的姿态控制和检测等内容.1 设计模型与数学模型研究如图1所示的磁悬浮系统,控制对象是铁磁性材料做成的球体.球的高度为h (t ),线圈电流为i (t ).磁悬浮动力学方程以及线圈回路电压方程分别为:md 2h (t )d t2=mg -k i (t )h (t )2L d i (t )d t=u (t )-Ri (t )(1) 其中m 为球的质量,g 为重力加速度,L 为线圈电感,R 为线圈电阻,k 为磁场和球之间的耦合系数.系统的输入为线圈电压u (t ),输出为球的高度h (t ).球与电磁铁间保持适当的距离时,电磁吸引力与重力平衡.如果球的高度下降太多,则磁场的作用力变弱而使球落下去.如果球离磁铁太近,则磁场作用又会太强而将球拉向磁铁,这也将破坏系统的稳定性.假定球的期望高度为h 0,该位置称为平衡点,此处重力和电磁吸引力相等.令加速度为零,求出维持该位置的期望电流.即:i 20=m g kh 203收稿日期:2009205224 作者简介:王华东(19692),男,江苏淮安人,江苏财经职业技术学院讲师,主要从事电子技术和自动控制研究.方程(1)为非线性方程.将模型在平衡点附近线性化,产生一组线性方程[1].为此引入状态变量:x 1=h x 2=d hd t x 3=i 则方程(1)变为:d x 1d t =x 2d x 2d t =g -kmx 3x 12(2)d x 3d t =u L -RLx 3 将方程(2)在工作点x 3=i 0,x 1=h 0处通过泰勒级数展开进行线性化[2],结果为:d x 1/d t d x 2/d t d x 3/d t=0102km ・i 20h 200-2k m ・i 0h 2-RLx 1x 2x 3+u 01/L.(3)2 应用M A TL A B 软件进行控制器设计假设球的质量为0.1kg ,线圈的电阻为10Ω,线圈电感为100m H ,耦合系数为0.02Nm 2/A ,期望高度为10cm.在MA TL AB 中建立系统的状态空间模型MagLev.>>m =0.1;g =9.81;R =10;L =0.1;k =0.02;h 0=0.1;>>i 0=h 03sqrt (m 3g/k );>>A =[010;23k 3i 0^2/(m 3h 0^3)0-23k 3i 0/(m 3h 0^2);00-R/L ];>>B =[0;0;1/L ];>>C =[100];>>D =0;>>Plant =ss (A ,B ,C ,D )>>MagLev =Plant在命令窗口输入:MagPoles =pole (MagLev )回车得到系统极点[2~3]:MagPoles =14.0071-14.0071-100.0000可见,线性化后悬浮系统的极点为±14,放大器的极点为-100.需加一个PD (比例微分)控制器来稳定系统.理论上PD 控制器的传递函数可写成如下形式:C 0(s )=k p +sk d其中k p 为比例增益,k d 为微分增益.由于高频噪声的影响,使得微分控制难以实现,实际应用中微分作用可以近似,并通过滤波消除噪声的影响.实际控制器的传递函数形式为:C 1(s )=k p +sk d sτf s +1=k p(τf +k d /k p )s +1τf s +1传递函数等价于一个超前控制器,其零点的时间常数为τr +k d /k p ,极点(滤波器)的时间常数为τf ,可见零点比极点慢.选择控制器零点在系统第一个稳定极点的右侧,此处取-10,滤波器的时间常数为25ms ,极点为-40.控制器的传递函数为:15 第3期 王华东等:磁悬浮系统的控制器设计C 1(s )=s +10s +40绘制系统根轨迹的程序为[3~4]:>>PD =tf (-13[110],[140]);>>rlocus (PD 3MagLev );>>axis (503[-32-44]);>>sgrid>>title (′Root locus of PD cont rolled magnetic levitator ′);>>xlabel (′Real axis ′);>>ylabel (′Imaginary axis ′)程序执行结果的根轨迹如图2所示图2 串联PD 控制器的磁悬浮系统根轨迹Fig.2 Root locus of PD controlled magnetic levitator在命令窗口输入:>>rlocus (tf (-13[110],[150])3MagLev )>>rlocfind (tf (-13[110],[150])3MagLev )光标变成十字线,将其放在实轴根轨迹上,介于不稳定极点与控制器零点之间[4],可由图中得到一个稳定的增益值.在虚轴和控制器零点之间中点附近,产生增益500.比例微分控制器影响系统的稳定性和暂态特性.而要改善系统的稳态特性可以采用PI (比例积分)控制系统.PI 控制器传递函数为:C 2(s )=k p +k i s =k p k i ・s +k i /k ps其有一个极点在原点处,一个零点在-k i /k p 处.如果和系统其他零极点相比,PI 控制器的零点与极点相距很近,则当PI 控制器和PD 控制器串联时,它对系统暂态特性的影响可以忽略.本控制系统中选择k i =k p =1.下面程序仿真了磁悬浮模型采用PID 控制器的闭环系统的脉冲响应[3].>>PD =tf (-13[110],[140]);>>PI =tf ([11],[10]);>>[y ,t ]=imp ulse (feedback (5003PI 3PD 3MagLev ,1));>>plot (t ,y );>>grid ;25太原师范学院学报(自然科学版) 第8卷 >>xlabel (′Time ′);>>ylabel (′Imp ulse response ′);>>title (′Imp ulse response of a magneti levitator ′);程序执行结果如图3所示.图3 磁悬浮系统线性模型的脉冲响应曲线Fig.3 Impulse response of a magnetic levitator3 结语由仿真结果可见磁悬浮球受到脉冲干扰会离开平衡位置,干扰消除后,在平衡位置上下减幅振动几次后可以回到原来位置,即系统是稳定的;系统自动调节速度较快,稳态误差较小.结果表明控制器是有效的.参考文献:[1] 薛定宇.控制系统计算机辅助设计———MA TLAB 语言及其应用[M ].北京:清华大学出版社,1996[2] 韩九强.MA TL AB 高级语言及其在控制系统中的应用[M ].西安:西安交通大学出版社,1998[3] Edward B ,Magrab.MA TLAB 原理与工程应用[M ].北京:电子工业出版社,2002[4] Friedland B.Advanced control system design[M ].Prentice Hall :Englewood Cliff s ,NJ ,1996The Design of Controller for Magnetic Levitation SystemW ang H u adong Xu Jun(Jiangsu Vocational and Technical College of Finance &Economics ,Huaian 223001,China ) 〔Abstract 〕 On t he basis of differential equation of magnetic levitation system ,int roduction of state variables and elicit t he state space equation.Calculate t he pole wit h MA TL AB ,t hen de 2termine t he parameters of t he PID cont roller.In t he end ,simulation t he imp ulse response of t he system.〔K ey w ords 〕 magnetic levitation ;MA TL AB ;PID cont roller ;imp ulse response【责任编辑:王映苗】35 第3期 王华东等:磁悬浮系统的控制器设计。
基于单片机的磁悬浮小球控制系统设计毕业论文

基于单片机的磁悬浮小球控制系统设计摘要随着越来越多的磁悬浮技术应用到现实生活中的各个领域,磁悬浮这个在几年前还是很陌生的一个词现在已经广为人知。
磁悬浮以悬浮力产生的原理分类可以分为超导磁悬浮和常导磁悬浮。
磁悬浮的控制系统是一个很复杂的问题。
本文研究的重点就是这两种磁悬浮的控制问题。
超导磁悬浮是利用处于超导状态下的超导体具有斥磁力的原理产生的。
超导磁悬浮的悬浮物体就是超导体本身,所以超导磁悬浮的控制重点就落在了超导体上。
本文从介绍超导磁悬浮的基本应用入手,逐步深入地介绍超导体的基本物理性质,然后介绍超导磁悬浮系统的控制方法、过程和原理。
与超导磁悬浮相比,常导磁悬浮的应用就更为广泛,因为常导磁悬浮的实现过程要简单得多。
常导磁悬浮可以分为应用电磁铁的磁悬浮和引用非电磁性磁铁(稀土永磁铁、普通磁铁等)的磁悬浮。
但是由于电磁铁便于控制和利用,所以利用电磁铁的磁悬浮义勇更为广泛。
本文在常导磁悬浮方面的研究是从一个实例入手,分析电磁铁式磁悬浮的原理,从而进一步研究电磁铁式磁悬浮的控制方法、过程和原理。
在本文的最后,我利用在大学里所学的知识,结合本文的研究重点——磁悬浮装置的控制问题,做出了一个简单的电磁悬浮装置。
这个悬浮装置的原理是利用对电磁铁电流的控制来实现一个铁球在空中的来回反复运动,达到视觉上的悬浮效果。
这虽然与实际的电磁铁悬浮控制方原理不同,但是利用这简单手段也能够达到相同的目的。
这个实例给了我们一个启示:简单的演示实验装置也能够说明磁悬浮列车等高新技术的工作原理,磁悬浮并不是遥不可及的。
关键词:常导磁悬浮,超导磁悬浮,磁悬浮的控制,演示实验装置,磁悬浮列车The design of control system of magnetic levitation ball basedon MCUABSTRACTAs more and more maglev technology is applied to each field in actual life, the word of magnetic suspension a several years ago was very strange has already widely known by the people. Magnetic suspension is classified and can be divided into superconductive magnetic suspension and electromagnetic magnetic suspension from the material which produces lift force. It is a very complicated problem to control the magnetism suspension system. The focal point that this text studies is that these two kinds of magnetic suspension demonstrate the design about question of controlling of the experimental provision.Superconductive magnetic suspension is to utilize the superconductor in superconductive state to upbraid magnetic force principles. To suspend object superconductor,so superconductive control focal point of magnetic suspension drop on the superconductor superconductive magnetic suspension. This text is from recommend that the using basically of superconductive magnetic suspension is started with, introduce the basic physical property of the superconductor , then the control method , course and principle to introduce superconductive magnetic suspension deeply progressively.Compared with superconductive magnetic suspension, the application that electromagnetic magnetic suspension is much more extensive , because the realization course that electromagnetic magnetic suspension is much simpler. Magnetic suspension that electromagnetic magnetic suspension and can be divided into the magnetic suspension which use the electro-magnet and quoted the non- electric magnetic magnet (tombarthite permanent magnet, ordinary magnet ,etc. ). But because the electro-magnet is more convenient and utilizes controlling, it is more extensive to use the magnetic suspension of the electro-magnet. The research in electromagnetic magnetic suspensionof this text is to proceed with a instance , analyse that according to the principle of electro-magnet type magnetic suspension , thus study electromagnetic type magnetic suspension control method , course and principle further.At the end of this text, I utilize knowledge studied in the university, combine the research focal point of this text - -Demonstrate the control question of the experimental provision , has made a simple electric magnetic suspension device in magnetic suspension. The principle of the device is to make use of control on electro-magnet electric current to realize moving repeatedly back and forth in the sky of an iron plate that this suspends, reach the result of suspending on the vision . This is it control square different principle to suspend with real electro-magnet, simple means this can achieve the the same goal too.This instance has given us one to enlighten: The simple demonstration experimental provision can state the operation principle of new and high technology , such as maglev train ,etc. too, magnetic suspension is not out of reach.KEY WORDS:electromagnetic magnetic suspension , superconductive magnetic suspension ,the control of magnetic suspension,demonstrate the experimental provision, the maglev train目录前言......................................................................... 错误!未定义书签。
磁悬浮控制系统设计 自动控制原理课程设计 哈工大

H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书(论文)课程名称:自动控制原理设计题目:控制系统的设计与仿真院系:航院控制科学与工程系班级:09401设计者:学号:109041指导教师:设计时间:2012.2.27-2012.3.14哈尔滨工业大学哈尔滨工业大学课程设计任务书目录一、题目要求与分析 (5)1.1 题目要求 (5)1.2 题目分析 (5)二、基于频率响应法的设计 (5)2.1 人工设计 (5)2.2 计算机辅助设计 (8)2.2.1 对被控对象仿真 (8)2.2.2 控制器的设计 (8)2.2.3 对校正后开环系统仿真 (11)2.2.4 对校正后闭环系统仿真 (12)2.3 校正装置电路图 (12)2.3.1 串联超前环节装置电路 (13)2.3.2 串联迟后环节装置电路 (13)三、基于根轨迹法的设计 (14)3.1 人工设计 (14)3.1.1 原系统根轨迹图 (14)3.1.2 期望主导极点 (14)3.1.3 控制器的设计 (15)3.1.4 校正后系统仿真分析 (16)3.2 计算机辅助设计(Sisotool工具箱) (17)四、基于PID控制器的设计 (18)4.1 PID控制器原理 (18)4.2 PID控制模型与仿真分析 (19)五、设计总结 (20)六、心得体会 (20)七、参考文献 (20)八、附录 (21)8.1 手工绘制渐近对数幅频特性曲线图(原系统、控制器以及校正系统) (21)8.2 任务书 (22)一、题目要求与分析1.1 题目要求已知:一主动磁悬浮系统固有部分输入电压至输出位置的传递函数化简如下:022000()1000G s s =-设计性能指标要求:(1)超调量10%p σ≤ (2)调整时间0.2s t s ≤1.2 题目分析用MALAB 绘制原传递函数0()G s 的单位阶跃响应图,如下图:24681012Step ResponseTime (sec)A m p l i t u d e图 1 原传递函数单位阶跃响应显然,系统发散,不满足题目中超调量及调整时间的要求,需对原传递函数进行校正。
基于单片机的磁悬浮小球控制系统设计

基于单片机的磁悬浮小球控制系统设计
采用霍尔元件检测小球,输位置出电信号经A/D转换反馈至单片机,运用单片机数字PID控制器来控制磁悬浮小球在磁场中的位置。
以单片机为核心,设计磁悬浮小球的控制电路设计,对控制算法进行研究,编写程序,通过传感器对小球位置的测量,利用通过单片机来实现对小球悬浮的稳定控制。
采用霍尔元件检测小球,输位置出电信号经A/D转换反馈至单片机,运用单片机数字PID控制器来控制磁悬浮小球在磁场中的位置。
给定数字量的作用是手动控制小球在磁场中的位置,根据给定量不同,小球的受力大小也随之改变。
单片机控制器主要是在接到传感器的反馈后通过把模拟信号转换成数字信号发给磁铁执行器从而控制磁场大小。
功率驱动则是改变驱动能力。
霍尔元件则是用于测量小球位置的传感器,并将其信号通过模数转换发送给单片机控制器
13电气工程及其自动化(2)班
1304102062
朱培喆。
磁悬浮控制系统设计
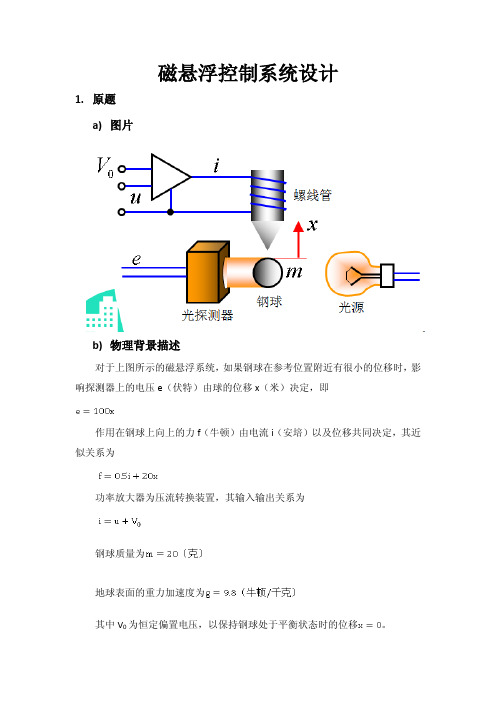
磁悬浮控制系统设计1.原题a)图片b)物理背景描述对于上图所示的磁悬浮系统,如果钢球在参考位置附近有很小的位移时,影响探测器上的电压e(伏特)由球的位移x(米)决定,即作用在钢球上向上的力f(牛顿)由电流i(安培)以及位移共同决定,其近似关系为功率放大器为压流转换装置,其输入输出关系为钢球质量为地球表面的重力加速度为其中V 0为恒定偏置电压,以保持钢球处于平衡状态时的位移。
c)问题的描述以电压u为控制信号,位移x为输出信号,建立系统的传递函数;以影响探测器输出电压e为反馈信号,并给定参考位移(输入)信号r,构成闭环反馈系统。
试设计适当的控制器,是的闭环系统满足下列性能指标:1)跟踪阶跃信号的稳态误差为零,跟踪单位斜坡信号的稳态误差为0.01;2)单位阶跃响应的超调量不大于30%,过度过程时间不大于1秒(△=2%)。
求控制器的传递函数。
2.问题推导a)零初始状态b)闭环传递函数以r为输入信号,x为输出信号,求r到x的传递函数。
;c)开环传递函数;3.问题求解a)问题分析稳态误差要求,跟踪阶跃函数时稳态误差为0,跟踪斜坡函数时稳态误差为0.01,所以应该串联一个积分环节用来增加系统型别,再串联一个放大环节来调整系统的稳态误差。
此开环传递函数对应根轨迹如图1。
图1有3条根轨迹,两条在实部,说明次闭环系统不稳定。
若加一零点与实部极点形成偶极子,由于系统的不精确,可能不能完全消除次极点的负面作用。
可以采用局部反馈校正。
在G(s)上加反馈校正环节,以改变整个系统的开环极点的位置。
b)系统方框图c)希望参数d)求解过程i.反馈校正环节;根轨迹如图2图2其频率特性如图3图3ii.迟后校正环节由此波特图知,剪切频率满足要求,但是相角裕度不满足要求,可采用迟后校正。
串联一环节。
波特图如图4图4 e)问题结果系统方框图为前向通道传递函数为:反馈通道传递函数为:开环传递函数为:闭环传递函数为:单位阶跃响应如图5图54.结论本系统满足性能指标,跟踪阶跃信号的稳态误差为零,跟踪单位斜坡信号的稳态误差为0.01,单位阶跃响应的超调量不大于16%,过渡时间为0.845秒(Δ=2%)。
磁悬浮寻北仪系统的自适应控制

工学硕士学位论文磁悬浮寻北仪系统的自适应控制王红梅哈尔滨工业大学2006年6月国内图书分类号:TP13国际图书分类号:681.5工学硕士学位论文磁悬浮寻北仪系统的自适应控制硕士研究生 :王红梅导师 :魏绍义高工申请学位 :工学硕士学科、专业 :导航、制导与控制所在单位 :控制理论与制导技术研究中心答辩日期 :2006年6月授予学位单位 :哈尔滨工业大学Classified Index:TP13U.D.C.: 681.5Dissertation for the Master Degree in EngineeringTHE ADAPTIVE CONTROL OF THE MAGNETIC NORTH-SEEKING SYSTEMCandidate:Wang Hong-MeiSupervisor:Senior Engineer. Wei Shao-Yi Academic Degree Applied for:Master of Engineering Specialty:Navigation, Guidance and ControlAffiliation: Center for Control Theory and Guidance TechnologyDate of Defence:June, 2006Degree-Conferring-Institution:Harbin Institute of Technology哈尔滨工业大学工学硕士学位论文- - I摘 要在人类的生产和生活实践中,地理方位信息是必不可少的,因此方位指示仪器的研究意义十分重大。
千百年来,人们为研究定位与定向技术进行了不懈的努力。
惯性技术和计算机控制技术的出现及其应用,为研制自主的、精密的方向指示仪器—惯性寻北系统提供了可能。
作为一种精密惯性仪表,寻北仪的定向精度在很大程度上取决于它所采用的陀螺的精度。
在本文中我们研究的这种磁悬浮陀螺寻北仪,就是通过采用自适应控制方法,利用磁悬浮技术实现对单自由度陀螺框架轴的无摩擦悬浮,旨在得到更高的寻北精度,同时提高定向速度。
基于PSO_磁悬浮球系统自适应灰预测控制

第40卷第5期Vol.40㊀No.5重庆工商大学学报(自然科学版)J Chongqing Technol &Business Univ(Nat Sci Ed)2023年10月Oct.2023基于PSO 磁悬浮球系统自适应灰预测控制马晓东1,魏利胜1,21.安徽工程大学电气工程学院,安徽芜湖2410002.安徽省电气传动与控制重点实验室,安徽芜湖241000摘㊀要:目的针对磁悬浮球系统非线性不稳定和滞后性的问题,提出一种基于粒子群优化的自适应灰色预测PID(Proportion Integration Differentiation )复合控制策略㊂方法通过在PID 控制模块的反馈环中引入具有等维新息特征的灰色预测器,对系统误差进行及时反馈修正,以提高控制系统的响应速度和鲁棒性;同时,融合粒子群智能算法对控制器参数迭代优化,以提高控制系统控制精度和抗干扰能力;最后,在MATLAB /Simulink 环境下搭建仿真平台进行对比实验㊂结果验证基于粒子群优化的自适应灰预测控制系统模型的超调量㊁峰值时间㊁调节时间显著改善㊂结论证实该策略可以有效抑制系统滞后性,具有良好的稳定性和鲁棒性㊂关键词:磁悬浮;粒子群算法;灰色预测;PID ;自适应中图分类号:TP273㊀㊀文献标识码:A ㊀㊀doi:10.16055/j.issn.1672-058X.2023.0005.003㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀收稿日期:2022-09-13㊀修回日期:2022-11-21㊀文章编号:1672-058X(2023)05-0016-09基金项目:安徽工程大学研究生教学改革与研究重点项目(2021JYXM001).作者简介:马晓东(1996 ),男,安徽芜湖人,硕士研究生,从事智能控制技术及应用研究.通讯作者:魏利胜(1978 ),男,安徽巢湖人,博士后,教授,从事图像识别与应用㊁嵌入式仪器仪表及系统研究.Email:lshwei_11@.引用格式:马晓东,魏利胜.基于PSO 磁悬浮球系统自适应灰预测控制[J].重庆工商大学学报(自然科学版),2023,40(5):16 24.MA Xiaodong WEI Lisheng.Adaptive grey predictive control of magnetic levitation ball system based on PSO J .Journal of Chongqing Technology and Business University Natural Science Edition 2023 40 5 16 24.Adaptive Grey Predictive Control of Magnetic Levitation Ball System Based on PSO MA Xiaodong 1 WEI Lisheng 1 21.School of Electrical Engineering Anhui Polytechnic University Anhui Wuhu 241000 China2.Anhui Key Laboratory of Electric Drive and Control Anhui Wuhu 241000 ChinaAbstract Objective Aiming at the problem of nonlinear instability and hysteresis of the magnetic levitation ball system an adaptive gray prediction composite control strategy based on particle swarm optimization was proposed.Methods A grey predictor with equal-dimension and new-info characteristics was introduced into the feedback loop of the PID control module to provide timely feedback correction of system errors so as to improve the response speed and robustness of the control system.And the particle swarm intelligence algorithm was integrated to iteratively optimize the controller parameters so as to improve the control accuracy and anti-interference ability of the control system.Finally a simulation platform was constructed in the MATLAB /Simulink environment for comparative experiments.Results The experimental results showed that the overshoot peak time and adjustment time of the adaptive grey predictive control system model based on particle swarm optimization were significantly improved.Conclusion It is confirmed that this strategy can effectively suppress the system hysteresis and has good stability and robustness.Keywords magnetic levitation particle swarm optimization grey prediction proportion integration differentiation PID adaptation1㊀引㊀言近些年来,随着磁悬浮技术迅速发展,具有非接触㊁低磨损㊁功耗低等特点的磁悬浮技术已被广泛应用于高端制造㊁医学㊁食品包装和轨道交通等领域㊂在实第5期马晓东,等:基于PSO磁悬浮球系统自适应灰预测控制际的生产和生活当中,磁悬浮列车㊁平面磁悬浮输送线等已被成熟使用,这给人类生活和工作带来方便和快捷㊂磁悬浮系统是一种典型的非线性开环不稳定系统,且存在着模型参数难以确定㊁易受外界干扰影响等难点,这使得传统的控制方法难以在磁悬浮系统中达到较好的控制效果[1]㊂为了满足磁悬浮系统稳定性㊁实时性的性能要求,设计一种高性能控制器具有十分重要的意义㊂为此,国内外相关的专家和学者在磁悬浮控制(Magnetic levitation control)策略上做了大量研究,且取得一定的研究成果㊂PID(Proportion Integration Differentiation)控制器凭借其控制结构简单㊁易于实现㊁鲁棒性强等优点,在过程控制中占有重要地位,被广泛应用在工业控制中㊂但PID无法自适应调整自身参数,无法保证磁悬浮系统达到良好的控制效果㊂故针对传统单一的PID控制系统响应速度慢和无法自适应在线调整参数的缺点,刘丽丽等[2]采用模糊控制和PID 控制方法组合的策略来对磁悬浮球进行控制,通过模糊推理机对系统的误差及误差变化率做出相应的判断决策,从而对PID的参数进行自适应在线调整,由此提高系统的控制精度和鲁棒性,但模糊控制器的性能优劣过度取决于规则和推理方式选择是否合理,而推理规则和参数固定不变又会降低系统自适应能力;王永涛等[3]针对传统PID控制器参数自适应调整难以达到最优,以及无法满足系统实时性等问题,提出在传统灰色预测模型上构建序列-残差联合灰色预测模型,以对预测误差二次灰色模型预测修正,从而实现对被控对象的快速精准控制㊂除对PID控制器进行参数优化之外,还有部分学者针对磁悬浮系统提出新的控制理论策略㊂Majewski等[4]建立神经网络控制系统,该神经网络由第一层非线性神经元和第二层线性神经元组成,通过实验表明其方法在控制精度和控制速度特性方面优于经典方法;Wei等[5]提出一种时变自动扰动抑制控制器(Time-varying Active Disturbance Rejection Control)方案来克服磁悬浮系统开环不稳定,通过现有线性自动扰动抑制控制器(Linear Active Disturbance Rejection Control,LADRC)加以改进并设计新TADRC 控制方案,提出一种时变增益的(TESO)可以较好保持扩张状态观测器(Extended State Observer,ESO)在瞬态过程中的估计性能;吕治国等[6]针对磁悬浮球运动状态发生变化时,控制器自适应能力较差的问题,提出一种非线性自适应控制方法,通过状态反馈线性化来构建系统模型,对模型参数进行在线估计辨识㊂考虑到单一的控制策略已无法满足高精度设备的控制要求,因此有国内外相关学者尝试将两种或两种以上的控制方法组合来获得更好的控制效果㊂王军晓等[7]针对外部干扰引起的磁悬浮球系统稳定性降低问题,提出一种将滑模预测控制器(Model Predictive Control,MPC)和预测控制(Predictive Control,PC)方法结合的控制策略,将等价输入干扰估计值与预测控制输出的最优控制率结合,从而得到最终的控制率,实现对参考点的快速准确跟踪,提高系统对扰动的鲁棒性;龚事引等[8]将PSO(Particle Swarm Optimization)算法应用于磁悬浮球系统中,针对磁悬浮球模糊控制系统中模糊量化因子难以调节问题,利用PSO算法对量化因子进行优化,结果表明该策略可以提高系统响应速度㊂以上众多的国内外专家学者分别从PID控制器参数优化㊁复合控制等不同角度对磁悬浮系统控制理论进行深入的研究,实现系统较快响应和具备一定抗扰动性㊂但针对磁悬浮系统是非线性系统且开环不稳定,易受外界扰动的特性,传统的控制策略仍很难达到预期的控制效果和实时要求,这使得在实际磁悬浮产品上难以应用推广[9-10]㊂为更好克服以上难点,提出一种基于粒子群优化的自适应灰色预测PID复合控制策略㊂首先通过对磁悬浮球进行动力学分析,从而建立数学模型;并针对PID参数无法自适应调整问题,采用粒子群算法对PID参数进行优化来提高控制器精度;以改善系统的响应速度和鲁棒性,在PID控制器的反馈环引入变步长灰色预测模块提高控制器自适应能力;最后,通过MATLAB/Simulink对所提方法进行实验,以验证所提方法能通过融合寻优速度快的粒子群算法来优化控制器参数来提高控制精度和增强系统抗扰动性,同时通过引入自适应灰预测模型思想来提高系统实时性和鲁棒性,具有应用价值和研究意义㊂2㊀磁悬浮球系统控制器设计2.1㊀磁悬浮球控制原理磁悬浮球系统工作原理是通过方向向上的电磁力来平衡悬浮钢球所受向下的重力㊂在电流和磁场的作用下,磁悬浮球主要受到两种外界力,即电磁铁对磁悬浮球的电磁力和地球对磁悬浮球的万有引力㊂当磁悬71重庆工商大学学报(自然科学版)第40卷浮球受到外界干扰力或自身承载的中重力发生变化时,磁悬浮球脱离预期轨道线路,此时基于YOLOv5(You Only Look Once)图像处理算法通过相机对磁悬浮球及位置进行识别和检测,将位移信号转换成数字信号并输入控制器中㊂磁悬球系统整体架构如图1所示㊂电磁铁驱动电路D /A 转换器相机计算机Fm g图1㊀磁悬浮球系统整体架构Fig.1㊀The overall structure of the magnetic levitationball system图1中控制器将获取的实时位置信号与磁悬浮球的指令位置进行对比后,计算出控制律,经过D /A 转换器和功率放大器处理后,对电磁铁绕组中的电流进行调节,使电磁铁产生相应大小的电磁力,从而改变磁悬浮球的运动状态,达到对磁悬浮球运动状态精准控制目的㊂2.2㊀磁悬浮球系统的建模在建立磁悬浮球的数学模型前,需做出以下假设:(1)忽略磁通漏磁,假设穿过铁芯的磁通无漏磁穿过,忽略边缘效应和磁悬浮球与电磁铁之间的磁阻㊂忽略线圈感抗及电涡流㊂(2)假设磁悬浮球是一个均匀的球体,磁力集中在其中心㊂基于以上假设,我们首先对磁悬浮球进行动力学分析,由牛顿第二运动定律,我们可以得到运动学方程,如式(1):mg -F (i ,x )=md x 2(t )d t 2(1)式(1)中:m 是磁悬浮球的质量(kg),g 是重力加速度(m /s 2),x 是气隙长度(m),为球心到电磁铁下表面间的距离,F (i ,x )表示电磁铁对磁悬浮球电磁力(N)㊂其中电磁铁是由带铁芯的螺线管构成,磁路中的磁阻如式(2):R (x )=2x μ0A(2)式(2)中:μ0是常量,表示空气的磁导率,数值大小为4π∗10-7H /m㊂A 是气隙的导磁截面积㊂由基尔霍夫定律可得如式(3):Ni =Φ(i ,x )R (x )(3)式(3)中:Φ(i ,x )表示单匝线圈的磁通量,i 表示线圈中电流,N 表示线圈匝数㊂由公式磁阻和公式磁动势得到电磁线圈的磁链,磁链表达式如式(4):ψ(i ,x )=NΦ(i ,x )=μ0AN 2i 2x(4)在静磁学中,根据毕奥-萨伐尔定律(Biot -SavartLaw),线圈的电流和磁链成正比关系式如式(5):ψ(i ,x )=Li(5)由电感的储能公式可得磁场的能量W m (i ,x )如式(6):W m (i ,x )=12L (i ,x )i 2=μ0AN 2i 24x(6)由式(6)可知,磁悬浮球受到的电磁力如式(7):F (i ,x )=- W m (i ,x )x=μ0AN 24()ix()2(7)式(7)中的μ0㊁A ㊁N 数为常数㊂根据基尔霍夫定律(Kirchhoff laws),将电磁铁线圈等效成电阻和电感串联电路㊂则电磁铁线圈回路中的电压可以如式(8):U i =Ri +L (x )d i d t(8)式(8)中,R 表示电磁铁线圈的电阻,L 表示电磁铁线圈电感,电感大小与电磁铁线圈结构和气隙长度有关,此处对电磁感应现象中产生的电涡流,线圈间漏磁情况进行忽略㊂当磁悬浮球在一个静态平衡工作点范围内稳定悬浮运动即为达到稳定悬浮状态时,将这个平衡工作点到电磁铁下表面间的距离设为x 0,对应流过的线圈电流为i 0,此时由牛顿运动定律可知小球所受到的重力和电磁力合力为零,可得到边界方程,如式(9):F (i 0,x 0)+mg =0(9)根据式(9),对系统F (i ,x )在平衡点x =x 0处进行泰勒展开,得到结果如式(10):81第5期马晓东,等:基于PSO 磁悬浮球系统自适应灰预测控制F (i ,x )=F (i 0,x 0)+F i (i 0,x 0)(i -i 0)+F x (i 0,x 0)(x -x 0)+12!F i (i 0,x 0)(i-i 0)2+(10)磁悬浮球系统在工作点x 0附近时,电流及位置变化极小,故可将系统F (i ,x )高次项省略,则系统F (i ,x )表达式如式(11):F (i ,x )=F (i 0,x 0)+μ0AN 22()i 0x20()(i -i 0)+μ0AN 2-2()i 20x 30()(x -x 0)(11)受力分析可知磁悬浮球的运动方程如式(12):m d 2xd t2=mg -F (i ,x )(12)将式(11)代入式(12)化简结果如式(13):m d 2x d t2=μ0AN 22()i 0x2()i +μ0AN 22()i20x30()x (13)将磁悬浮球系统的位置刚度系数㊁线圈电流刚度系数分别设为k x ㊁k i ,其表达式如式(14)和式(15):k x =F x (i 0,x 0)=μ0AN 2i 202x 30(14)k i =F i (i 0,x 0)=μ0i 0AN 22x 20(15)对公式两边进行拉普拉斯变换,结果如式(16):ms 2X (s )=-k i I (s )+k x X (s )(16)在忽略外界干扰力的情况下,由式(16)可以推导出输入为线圈电流i 到输出为当前球体位置x 的开环传递函数,经拉普拉斯变换后表达式如式(17):X (s )I (s )=-k i ms 2-k x(17)将磁悬浮球的相关参数代入,得出系统数学模型如式(18):G (s )=X (s )I (s )=-16.36s 2-642.66(18)2.3㊀基于粒子群算法优化的自适应灰预测控制器设计基于粒子群算法优化的自适应灰预测控制器结构图如图2所示㊂图2中r 代表系统输入量,y 代表系统输出量,y ∗代表系统预测输出,e ∗=r -y ∗为系统偏差值㊂粒子群算法输入r磁悬浮球系统预测步长自调节灰色预测器输出e *P I Dy *yk p k d ki 图2㊀基于粒子群算法优化的自适应灰预测控制器结构Fig.2㊀The structure diagram of adaptive grey predictioncontroller based on particle swarm optimization基于粒子群算法优化的自适应灰预测控制器是在PID 控制器的闭环反馈回路中引入灰色预测器,将磁悬浮球控制系统的输出y 作为采样信息,设定适当的误差参考阈值,根据系统实际误差值的大小,自适应调整灰色预测控制器的预测步长,采用不同的预测步长实现前向和后向预测,从而提高灰色预测控制器的预测精度;另通过PSO 算法对控制器的参数进行迭代寻优,确定最优控制器参数,以实现对磁悬浮球的自适应控制㊂2.3.1㊀自适应灰色预测控制器的设计灰色预测控制器的核心是灰色预测模型的建立㊂灰色微分模型一般记为GM (n ,m ),其中n ㊁m 含义是常微分方程的阶数㊁灰色变量个数,即用n 阶微分方程对数量为m 的灰色变量建立模型㊂当n ㊁m 取值较大时,预测精度可能不会得到提高,故选择GM (1,1)作为灰色预测模型㊂灰色预测模型主要是由累积生成操作(AGO)㊁灰建模(GPM)以及累减生成操作(IAGO)构成[11-18]㊂首先,采集原始数据序列,y 0={y 0(1),y 0(2), ,y 0(n )}表示被控对象的输出序列,即GM (1,1)模型的输入量㊂其次,对序列进行累加生成操作(AGO),转换得到一次累加生成序列,如式(19):y(1)(k )=ðkm =1y (0)(m )(19)式(19)中,k =2, ,n 是序列数㊂再次,序列累加生成后,进行灰建模操作㊂对新序列y 1={y 1(1),y 1(2), ,y 1(n )}进行背景值计算,背景91重庆工商大学学报(自然科学版)第40卷值公式如式(20):z (1)(k )=θy (1)(k )+(1-θ)y (1)(k -1)(20)式(20)中,θ为常数,本文将其取值为0.5㊂将其代入式(20),则新序列的MAIN 序列如式(21):z (1)(k )=0.5y (1)(k )+0.5y (1)(k -1)(21)之后,通过一阶微分方程来构建GM (1,1)灰预测模型,一阶微分方程可如式(22):y (0)(k )+az (1)(k )=b(22)式(22)中:y (0)(k )表示灰导数,a 表示发展系数,其大小及符号反映y (1)(k )发展态势㊂z (1)(k )表示白化背景值序列,b 表示具有灰色信息覆盖的作用量,简称灰作用量㊂结合式(21)和式(22)可得结果如式(23):y (0)(k )(1+0.5a )+ay (1)(k -1)=b (23)然后,求解最优参数,设M =a b éëêêùûúúB =-z (1)2()-z (1)3()-z (1)N ()111éëêêùûúúT令y n =⌊y (0)(2),y (0)(3), ,y (0)(n )」,则一阶灰色微分方程可表示为y n =B ∗M ㊂由最小二乘法可以获得最优参数M ,求出a ㊁b ㊂求解公式如式(24):M =(B T B )-1B T y n(24)最后,进行累减生成操作(IAGO )所得结果如式(25):y (1)(k )-y (1)(k -1)=y (0)(k )(25)结合式(23) 式(25)可得,预测结果如式(26)所示:y (0)(k )=1-0.5a 1+0.5a ()y (0)(k -1),k >2y (0)(k )=b -ay (0)(1)1+0.5a ,k =2ìîíïïïï(26)综上,由GM (1,1)派生模型内涵型GM (1,1,C )可知,被控对象灰预测模型序列未来预测值可表达如式(27):y ∗(k )=1-0.5a1+0.5a()(n +p -2)b -ay (0)(1)1+0.5a(27)式(27)中:p 是模型序列预测步长,n 为数据序列长度㊂本文原始数据序列长度为n =5,故原灰色预测模型又可以进一步描述如式(28):y ∗(k )=1-0.5a1+0.5a()(3+p )b -ay (0)(1)1+0.5a(28)传统的灰色预测控制器虽然可以较好的降低超调量,但响应时间却被延长,为了让系统响应更加迅速,故对固定步长进行自适应调整,让系统输入值与输出值进行比较得出系统误差e (k ),设置最小误差阈值e min为0.1和最大误差阈值e max 为0.8,当误差e (k )大于e max ,选择负数预测步长,实现后向预测,增加控制量,加快系统响应速度㊂当误差e (k )小于e min ,选择正数预测小步长,实现前向预测,降低超调量,当误差在最大阈值和最小阈值之间,选择正数预测大步长㊂预测步长p 自适应具体表达式如式(29):p =-8e (k )>0.840.1<e (k )<0.812e (k )<0.1ìîíïïïï(29)构建GM (1,1)等维新息模型,使系统得到更为精准的预测输出,将系统给定输入r (k )与灰色预测控制器得出预测输出y ∗(k )进行作差,得到差值e ∗(k )即为系统的误差预测值㊂最后,将e ∗(k )作为PID 控制器的输入,经过控制器得出作用于磁悬浮球的系统输出量u (k ),由此实现对磁悬浮球系统的自适应控制㊂2.3.2㊀等维新息模型融合信息的快速准确获取关系到预测精度高低㊂灰色预测策略特点之一就是通过获取少量数据信息建模来对系统未来行为进行预测㊂本文在GM (1,1)模型采集信息时引入等维新息模型㊂等维新息模型原理图如图3所示㊂原数据序列Y (0){y (0)(1),y (0)(2),…y (0)(n )}序列更新Y (0){y (0)(0),y (0)(1),…y (0)(n -1)}下一采样时间新数据序列Y (0){y (0)(1),y (0)(2),…y (0)(n )}新数据y (0)(0)图3㊀等维新息模型原理图Fig.3㊀Schematic diagram of the equal dimension newinformation model图3中,首先,将采集到的原系统输出量作为数据原序列;再用采集到的新数据替代原序列中的部分旧2第5期马晓东,等:基于PSO磁悬浮球系统自适应灰预测控制数据,以此来让序列不断更新,使灰色预测控制器可以在仍维持原始数据序列维度不变前提下,达到提高预测精度的目的㊂2.3.3㊀粒子群算法的参数优化粒子群优化算法是一种基于群体智能随机优化算法,具有简单易实现,寻优速度快特点[19-22]㊂粒子群优化算法速度和位置更新公式如式(30)和式(31):v ij(k+1)=wv ij(k)+c1r1(k)[p ij(k)-x ij(k)]+c2r2(k)[g ij(k)-x ij(k)](30)x ij(k+1)=x ij(k)+v ij(k+1)(31)式(30)和式(31)中,v ij(k+1)表示速度更新输出值,x ij(k+1)表示位置更新输出值㊂下标i表示微粒,j表示微粒维数;k表示迭代次数,w表示惯性权重,c表示学习因子,为非负常数,r表示在区间[0,1]内均匀分布的随机数;p表示粒子寻找到个体最优值,g表示为粒子群寻优所得全局最优值,v表示速度,x表示位置㊂粒子群算法对PID控制器的优化本质核心是确定一组合适的参数,使控制性能达到最优㊂粒子群算法设计流程图如图4所示㊂开始初始化粒子群的速度和位置计算各粒子的适应度并更新个体最优和全局最优值更新所有粒子的速度和位置是否满足终止条件结束是否图4㊀粒子群算法设计流程图Fig.4㊀Flow chart of the particle swarm algorithm design首先,对参数进行设置:设置惯性因子㊁粒子群规模㊁最大迭代次数等,确定ITAE指标作为优化算法适应度函数,PSO算法产生初始化的粒子群,随机产生粒子的初始速度和初始位置值㊂其次,根据适应度函数计算粒子对应的适应度值:计算得出粒子个体极值和粒子群群体极值㊂再根据速度及位置公式对粒子和粒子群的速度和位置进行迭代更新,计算更新后的适应度函数值,更新个体极值和群体极值㊂并与历史最优适应度进行比较,选取最好的将其作为当前迭代最优适应度值㊂最后,将性能指标信息传递至PSO中:根据预设定最大迭代次数和适应度下限值判断性能指标是否满足终止条件,若不满足,则继续对粒子群进行速度和位置更新操作,再对更新后产生的粒子群的速度和位置适应度进行比较,直至寻找到满足终止条件的粒子群结束㊂3㊀灰预测控制稳定性分析假设系统线性模型如式(32):x㊃(t)=A x(t)+B u(t)y(t)=C x(t){(32)式(32)中,x(t)ɪR n表示状态变量,u(t)ɪR m表示控制量,y(t)ɪR r表示系统输出量㊂A㊁B㊁C分别表示系统矩阵㊁控制矩阵㊁输出矩阵㊂系统误差公式如式(33):e(t)=r(t)-y(t)(33)令灰色预测控制器输出值为y∗(t),预测误差则如式(34):e∗(t)=r(t)-y∗(t)Δe∗(t)=e㊃∗x(t)=r㊃(t)-y㊃∗(t) {(34)已知PID控制器的输出公式如式(35):u(t)=u(t-T)+k1ˑe∗(t)+k2ˑΔe∗(t)+k3ʏe∗(t)(35)式(35)中,t和T为采用时间和采样周期㊂假设预测误差界于某个正常数Z,如式(36)㊁式(37)所示㊂误差界值Z越小,则意味着灰预测控制系统稳定性越好㊂y∗(t)-y(t) λɤZ(36)e∗(t)-e(t) λɤZ(37)将线性状态方程式(32)代入,由式(33) 式(37)可得结果如式(38):e(t)=r(t)-y(t)=e(t-T)-㊀ʏt0CΦ(t-τ)B k1e∗(τ)+k2e㊃∗(τ)+k3ʏτ0e∗(σ)dσ[]dτ(38)12重庆工商大学学报(自然科学版)第40卷令H (t -T )=C Φ(t -τ)B ,则化简如式(39):ʏtH (t -T )k 2e㊃∗(τ)d τ=H (0)k 2e ∗(t )-㊀ʏt∂∂τH (t -τ)k 2[]e ∗(τ)d τ(39)将式(39)代入式(38),化简结果如式(40):e (t )=e (t -T )-H (0)k 2e ∗(t )-H (t -T )k 1-∂∂τH (t -τ)k 2[]{}e ∗(τ)d τ-ʏτ0H (t -τ)k 3e∗(σ)d σd τ(40)为便于本文讨论分析验证,阐述本文所用函数如式(41)㊁式(42)㊁式(43)㊁式(44)所示:f (t ) λ=supe-λtf (t ) (41) f (t ) ɕ=sup f (t ) (42)m 1=sup H (t -τ)k 1-∂∂τH (t -τ)k 2[]ɕ(43)m 2=sup H (t -τ)k 3 ɕ(44)对式(40)两边进行处理,结果如式(45): I +H (0)k 2 ㊃ e (t ) ɤ e (t -T ) +㊀ H (0)k 2 e ∗(t )-e (t ) +㊀ʏt 0m 1e ∗(τ)-e (τ) d τ+ʏt 0m 1e (τ) d τ+㊀ʏt0ʏτ0b 2e ∗(σ)-e (σ) d σd τ+㊀ʏt0ʏτ0b 2e ∗(σ)-e (σ) d σd τ+㊀ʏtʏτb 2e (σ) d σd τ(45)对式(45)化简结果如式(46):I +H (0)k 2 ㊃ e (t ) λɤ e (t -T ) λ+㊀ H (0)k 2 Z +m 11-e -λt λZ +m 11-e -λtλ e (t ) λ+㊀m 21-e -λtλ()2Z +m 21-e -λtλ()2e (t ) λ(46)令:η1(t )= I +H (0)k 2 -m 11-e -λt λ-m 21-e -λt λ()2éëêêùûúú-1η2(t )= H (0)k 2 +m 11-e -λt λ+m 21-e -λtλ()2对式(46)整理结果如式(47):e (t ) λɤη1(t ) e (t -T ) λ+η1(t )η2(t )Z(47)则当λ足够大时,误差lim t ңɕe (t ) λ收敛于正常数㊂4㊀实验验证及结果分析为了验证本文所设计控制器在磁悬浮球系统中有效性和控制效果,采用MATLAB /Simulink 进行仿真研究,选择超调量σ,峰值时间t r ,调节时间t s 作为衡量控制器性能的指标㊂设定PID 控制器参数k p ㊁k i ㊁k d 的初始值为-480㊁-3200㊁-10;设置粒子群算法参数,惯性因子w =0.6,学习因子c 1与c 2均为2,粒子群规模为20,最大迭代次数为25,粒子速度范围为[-1,1],维数为3㊂采用ITAE 指标作为优化算法适应度函数,其函数公式为ʏɕ0t e (t )d t ㊂采用阶跃函数和正弦函数作为输入激励信号分别来衡量系统的控制器性能优劣和轨迹跟踪能力,其仿真结果分别如图5所示㊁图6所示㊂1.21.00.80.60.40.20.10.20.30.40.50.6位置/m mt /sP I D 方法文本方法文献2方法阶跃信号图5㊀阶跃输入信号下磁悬浮球响应曲线图Fig.5㊀The response curve of magnetic levitation ballunder step input signal3.02.52.01.51.00.50.51.01.52.02.53.0位置/m m t /sP I D 方法文本方法文献2方法正弦信号图6㊀正弦信号下磁悬浮球轨迹对比图Fig.6㊀The comparison chart of magnetic levitation balltrajectory under sinusoidal signal由图5可知,磁悬浮球系统在输入为阶跃响应信号的作用下,PID 策略可以使系统实现较好的稳定,但依然存在较大的超调量㊂本文引入灰色预测思想,能够明显的降低超调量,文献[2]方法为模糊PID 控制策22第5期马晓东,等:基于PSO磁悬浮球系统自适应灰预测控制略,文献[2]方法调节时间相比较于原PID方法有一定程度的减少,但仍待改善,本文引入粒子群优化算法,其调节时间明显要低于其他两种策略㊂三种控制方法在阶跃输入信号下暂态性能对比如表1所示㊂表1㊀暂态性能对比表Table1㊀Comparison of transient performance 方㊀法指㊀标超调量(σ/%)峰值时间(t r/s)调节时间(t s/s) PID19.080.0770.245文献[2]14.20.0650.205本文方法12.090.0170.033㊀注:加粗表示在该指标下效果最佳㊂为检验本文控制器在目标跟踪上响应速度和准确性的表现,故对其进行位置跟踪测试㊂给定磁悬浮球正弦目标轨迹信号,正弦信号是一种典型的周期信号,将其作为位置跟踪测试信号,其目标轨迹函数如式(48):y=sin4πt+1.5(48)此外在同等条件下,使用文献[2]方法㊁PID方法和本文方法对磁悬浮球模型进行仿真测试,其轨迹跟踪效果如图6所示㊂由图6正弦轨迹位置响应曲线图可以看出磁悬浮球系统在本文方法控制器作用下跟踪效果表现最好,期望目标轨迹与实际位置误差最小,响应速度快㊁滞后小㊂同时,从图6中可以看出本文控制方法的抗饱和能力反应速度和跟踪能力都优于文献[2]和PID控制器㊂5㊀结㊀论本文针对磁悬浮球系统实时性和稳定性较差问题,设计了一种基于粒子群优化的自适应灰预测控制策略㊂通过在PID控制模块的反馈环中引入等维新息灰色预测模型,实现对系统误差进行及时反馈修正,提高控制系统的响应速度和鲁棒性;并融入粒子群算法对控制器参数迭代优化,以提高控制系统控制精度和抗干扰能力,实现精准快速控制㊂通过仿真对比实验结果显示本文控制策略模型的超调量㊁峰值时间㊁调节时间显著改善,为其在实际应用中奠定良好的理论研究和实际应用价值㊂参考文献References1 ㊀周丹峰李杰余佩倡等.磁浮交通轨排耦合自激振动分析及自适应控制方法J .自动化学报2019 45122328 2343.ZHOU Dan-feng LI Jie YU Pei-chong et al.Analysis and adaptive control method of coupled self-excited vibration of magnetic levitation traffic rails J .Acta Automatica Sinica 2019 45 12 2328 2343.2 ㊀刘丽丽左继红.磁悬浮球系统模糊PID参数自调整控制方法J .控制工程2021 28 2 354 359.LIU Li-li ZUO Ji-hong.Fuzzy PID parameter self-adjustment control method for magnetic levitation ball system J .Control Engineering 2021 28 2 354 359.3 ㊀王永涛肖俊辰.基于改进灰色预测单神经元PID的URV伺服控制系统研究J .兵器装备工程学报2021 428251 257.WANG Yong-tao XIAO Jun-chen.Research on URV servo control system based on improved grey prediction single neuron PID J .Chinese Journal of Weaponry and Equipment Engineering 2021 42 8 251 257.4 ㊀MAJEWSKI P PAWUS D SZURPICKI K et al.Towardoptimal control of a multivariable magnetic levitation system J .Applied Sciences 2022 12 2 674 678.5 ㊀WEI W XUE W Li D.On disturbance rejection in magneticlevitation J .Control Engineering Practice 2019 82124 35.6 ㊀吕治国龙志强.磁悬浮球系统的非线性自适应控制方法J .控制工程2020 27 1 127 133.LV Zhi-guo LONG Zhi-qiang.Nonlinear adaptive control method of magnetic levitation ball system J .Control Engineering 2020 27 1 127 133.7 ㊀王军晓陈林杰俞立.基于等价输入干扰滑模观测器的磁悬浮球系统模型预测控制J .控制理论与应用2021 381 137 146.WANG Jun-xiao CHEN Lin-jie YU Li.Model predictive control of maglev ball system based on equivalent input disturbance sliding mode observer J .Control Theory and Application 2021 38 1 137 146.8 ㊀龚事引李丹.基于粒子群优化的磁悬浮球系统的模糊强化学习控制J .石河子科技2021 1 41 43.GONG Shi-yin LI Dan.Fuzzy reinforcement learning control32。
