离散傅里叶变换的分析与研究 开题报告
实验离散时间傅里叶变换和离散傅里叶变换
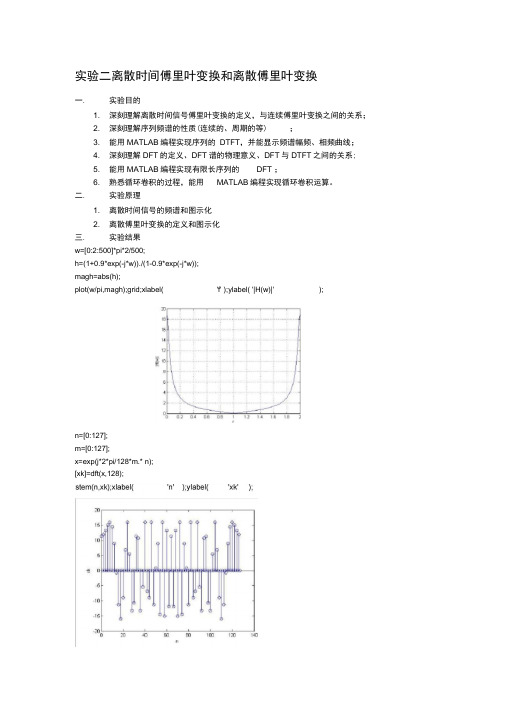
实验二离散时间傅里叶变换和离散傅里叶变换一.实验目的1. 深刻理解离散时间信号傅里叶变换的定义,与连续傅里叶变换之间的关系;2. 深刻理解序列频谱的性质(连续的、周期的等) ;3. 能用MATLAB编程实现序列的DTFT,并能显示频谱幅频、相频曲线;4. 深刻理解DFT的定义、DFT谱的物理意义、DFT与DTFT之间的关系;5. 能用MATLAB编程实现有限长序列的DFT ;6. 熟悉循环卷积的过程,能用MATLAB编程实现循环卷积运算。
二.实验原理1. 离散时间信号的频谱和图示化2. 离散傅里叶变换的定义和图示化三.实验结果w=[0:2:500]*pi*2/500;h=(1+0.9*exp(-j*w))./(1-0.9*exp(-j*w));magh=abs(h);plot(w/pi,magh);grid;xlabel( 'f' );ylabel( '|H(w)|' );n=[0:127];m=[0:127];x=exp(j*2*pi/128*m.* n);[xk]=dft(x,128);n=[0:127];m=[0:127];x=cos(2*pi/128*m.* n);[xk]=dft(x,128);stem( n,xk);xlabel( 'n' );ylabel( 'xk');« 0n=[0:127];m=[0:127]; [xk]=dft(x,128);stem( n,xk);xlabel( 'n' );ylabel( 'xk');n=[0:127];m=[0,127];x=s in(n);[xk]=dft(x,128);stem( n,xk);xlabel( 'n' );ylabel( 'xk');fC. ------------------------ ----------- ------------- ------------ ------------ ------------ -------------40 - -■3D ・-2D =-1D I- ii j | i■西k -____ g , ,上,___________注X] Sfl EC IDO 120 '40n=[0:127];m=[0:127];x=cos( n);[xk]=dft(x,128);stem( n,xk);xlabel( 'n' );ylabel( 'xk');n=[0:127];m=[0:127];x=n;[xk]=dft(x,128);stem( n,xk);xlabel( 'n' );ylabel( 'xk');n=[0:9];x1=[1,1,1,1,1,0,0,0,0,0];x2=[1,1,1,1,1,-1,-1,-1,-1,-1];[y]=circ on vt(x1,x2,10);stem( n,y);xlabel( 'n' );ylabel( 'y');。
离散傅立叶变换DFT实验报告

实验一 离散时间系统的时域分析一、实验目的1. 运用MATLAB 仿真一些简单的离散时间系统,并研究它们的时域特性。
2. 运用MATLAB 中的卷积运算计算系统的输出序列,加深对离散系统的差分方程、冲激响应和卷积分析方法的理解。
二、实验原理离散时间系统其输入、输出关系可用以下差分方程描述:∑=∑=-=-M k k N k k k n x p k n y d 00][][当输入信号为冲激信号时,系统的输出记为系统单位冲激响应 ][][n h n →δ,则系统响应为如下的卷积计算式:∑∞-∞=-=*=m m n h m x n h n x n y ][][][][][ 当h[n]是有限长度的(n :[0,M])时,称系统为FIR 系统;反之,称系统为IIR 系统。
在MA TLAB 中,可以用函数y=Filter(p,d,x) 求解差分方程,也可以用函数 y=Conv(x,h)计算卷积。
例1clf;n=0:40;a=1;b=2;x1= 0.1*n;x2=sin(2*pi*n);x=a*x1+b*x2;num=[1, 0.5,3];den=[2 -3 0.1];ic=[0 0]; %设置零初始条件y1=filter(num,den,x1,ic); %计算输入为x1(n)时的输出y1(n)y2=filter(num,den,x2,ic); %计算输入为x2(n)时的输出y2(n)y=filter(num,den,x,ic); %计算输入为x (n)时的输出y(n)yt= a*y1+b*y2;%画出输出信号subplot(2,1,1)stem(n,y);ylabel(‘振幅’);title(‘加权输入a*x1+b*x2的输出’);subplot(2,1,2)stem(n,yt);ylabel(‘振幅’);title(‘加权输出a*y1+b*y2’);(一)、线性和非线性系统对线性离散时间系统,若)(1n y 和)(2n y 分别是输入序列)(1n x 和)(2n x 的响应,则输入)()()(21n bx n ax n x +=的输出响应为)()()(21n by n ay n y +=,即符合叠加性,其中对任意常量a 和b 以及任意输入)(1n x 和)(2n x 都成立,否则为非线性系统。
实验四离散傅立叶变换DFT

实验四离散傅立叶变换DFT实验四离散傅里叶变换(DFT )一实验目的(1)理解信号变换的基本概念(2)理解离散傅立叶变换的基本概念二实验原理及实例分析 1、离散傅里叶变换傅里叶变换是信号分析和处理的重要工具。
有限长序列作为离散信号的一种,在数字信号处理中占有着极其重要的位置。
对于有限长序列,离散傅立叶变换不仅在理论上有着重要的意义,而且有快速计算的方法-快速傅立叶变换FFT 。
所以在各种数字信号处理的运算方法中,越来越起到核心的作用。
1.1 傅里叶变换的几种形式1、非周期连续时间信号的傅里叶变换非周期连续时间信号)(t x 的傅立叶变换)(ωj X 可以表示为)(ωj X =dt e t x tj ?∞∞--ω)(逆变换为ωωπωd j x t x tj ?∞∞-=)(21)(在这里,ω是模拟角频率。
可以看到,时域的连续函数造成频域的非周期谱,时域的非周期性造成频域的连续谱。
结论:非周期连续时间函数对应于一非周期连续频域变换函数。
2、周期连续时间信号的傅里叶变换周期为T 的周期性连续时间信号)(t x 傅立叶变换是离散频域函数,可表示为-=22)(1)(T T tjm d e t x Tjm X ωωω 逆变换为ωωωd ejm X t x tjm m ∑∞-∞==)()(这就是经常称之为傅里叶级数的变换形式。
在这里,ω也是模拟角频率。
可以看到,时域的连续函数造成频率域的非周期谱,频域函数的离散造成时域函数的周期性。
结论:周期连续时间函数对应于一离散非周期频域变换函数。
3、非周期离散时间信号)(n x 的傅立叶变换)(ωj e X 可以表示为∑∞-∞=-=nnj j e n x e X ωω)()(逆变换为ωπωππωd e e X n x n j j ?-=)(21)( 在这里,ω是数字频率,它和模拟角频率的关系为T Ω=ω。
可以看到,时域的取样对应于频域的周期延拓,而时域函数的非周期性造成频域的连续谱。
实验六 离散傅里叶变换

数学与软件科学学院实验报告学期:13至14 第_2学期 2014年4月7日课程名称:数字信号处理专业:信息与计算机科学实验编号:6 实验项目:6指导教师姓名:学号:实验成绩: A实验六离散傅里叶变换一、实验目的(1) 了解离散傅里叶的定义;(2) 通过实验掌握离散傅里叶变换后的幅度和相位特性;(3) 学会使用cirshif()函数。
二、实验内容(1) 求DFT,设x(n)={1,0,1,1},计算x(n)的4点,8点DFT,画出x(k) 的幅度和相位特性曲线;(2) 利用cirshif()函数实现循环移位,x(n)=0.8n,0<=n<=10,绘制y(n)=x(n+7)R(n);(3) 线性卷积和循环卷积的计算已知x1(n)={1,2,3},长度N1=3,x2(n)={4,3,2,1},长度N2=4①计算两序列的线性卷积;②分别计算两序列的4,5,6,7,8点循环卷积(N>=N1+N2-1时,循环卷积等于线性卷积)。
三、实验准备安装MATLAB的计算机系统。
四、实验步骤及结果一>.求DFT,设x(n)={1,0,1,1},计算x(n)的4点,8点DFT,画出x(k) 的幅度和相位特性曲线;实验代码如下:xn=[1 0 1 1];xk4=fft(xn,4);xk8=fft(xn,8);magX1=abs(xk4);angX1=angle(xk4);magX2=abs(xk8);angX2=angle(xk8);subplot(2,2,1);stem(magX1,'.');ylabel('幅度');subplot(2,2,2);stem(angX1,'.');ylabel('相位');subplot(2,2,3);stem(angX2,'.');ylabel('幅度');subplot(2,2,4);stem(angX2,'.');ylabel('相位');运行后得到的图像如下:二>.利用cirshif()函数实现循环移位,x(n)=0.8n,0<=n<=10,绘制y(n)=x(n+7)R(n);实验代码如下:a=0,b=-7;n=[0:10];x=(0.8).^n;subplot(2,1,1);stem(n,x);xlabel('n');ylabel('x(n)');title('x=(0.8).^n');y=circshift(x,[a,b]);subplot(2,1,2);stem(n,y);xlabel('n');ylabel('y(n)');title('y=x(n+7)R(n)');程序运行后得到的图像如下所示:三>.已知x1(n)={1,2,3},长度N1=3,x2(n)={4,3,2,1},长度N2=4①计算两序列的线性卷积;实验代码:xn1=[1,2,3];xn2=[4,3,2];yn=conv(xn1,xn2);stem(yn);xlabel('序列长度');ylabel('yn=xn1*xn2');title('线性卷积');运行后得到的结果为:②分别计算两序列的4,5,6,7,8点循环卷积(N>=N1+N2-1时,循环卷积等于线性卷积)。
傅里叶变换应用的开题报告

傅里叶变换应用的开题报告傅里叶变换应用的开题报告引言:傅里叶变换是一种重要的数学工具,广泛应用于信号处理、图像处理、通信等领域。
本文将探讨傅里叶变换的原理及其在实际应用中的重要性,并介绍一些典型的应用案例。
一、傅里叶变换的原理傅里叶变换是一种将时域信号转换为频域信号的数学变换方法。
它基于傅里叶级数的思想,将一个周期信号分解为一系列频率不同的正弦波的叠加。
傅里叶变换可以将信号从时域转换到频域,从而更好地理解信号的频谱特性。
二、傅里叶变换在信号处理中的应用1. 频谱分析傅里叶变换可以将信号在频域上进行分析,帮助我们了解信号的频率分布情况。
通过分析信号的频谱,我们可以得到信号的频率成分、频率强度等信息,从而对信号进行合理的处理和优化。
2. 滤波器设计傅里叶变换在滤波器设计中有着重要的应用。
通过将信号转换到频域,我们可以对信号进行滤波处理,去除不需要的频率成分,从而实现信号的降噪、去除干扰等目的。
3. 信号压缩傅里叶变换可以将信号从时域转换到频域,通过对频域信号进行处理,可以实现信号的压缩。
频域上的信号通常可以用较少的频率成分来表示,从而减小信号的存储空间和传输带宽。
三、傅里叶变换在图像处理中的应用1. 图像滤波傅里叶变换在图像滤波中有着广泛的应用。
通过将图像转换到频域,我们可以对图像进行滤波处理,去除图像中的噪声、增强图像的细节等。
2. 图像压缩傅里叶变换在图像压缩中也起到了重要的作用。
通过将图像转换到频域,我们可以利用频域上的特性对图像进行压缩,减小图像的存储空间和传输带宽。
3. 图像识别傅里叶变换在图像识别中的应用也十分重要。
通过将图像转换到频域,我们可以提取图像的频率特征,从而实现对图像的识别和分类。
四、傅里叶变换在通信中的应用1. 调制与解调傅里叶变换在调制与解调中有着重要的应用。
通过将信号转换到频域,我们可以对信号进行调制或解调处理,实现信号的传输和接收。
2. 信道估计傅里叶变换在信道估计中也扮演着重要的角色。
离散时间信号与系统的傅立叶分析 (实验报告)

电子信息工程系实验报告课程名称:数字信号处理实验项目名称:离散时间信号与系统的傅立叶分析 实验时间:班级:通信091 姓名:刘跃维 学号:实 验 目 的:用傅立叶变换对离散时间信号和系统进行频域分析实 验 环 境:计算机 MATLAB 软件原理说明:对信号进行频域分析就是对信号进行傅立叶变换。
对系统进行频域分析即对它的单位脉冲响应进行傅立叶变换,得到系统的传输函数;也可以由差分方程经过傅立叶变换直接求它的传输函数;传输函数代表的就是系统的频率响应特性。
但传输函数是w 的连续函数,计算机只能计算出有限个离散频率点的传输函数值,因此得到传输函数以后,应该在π2~0之间取许多点,计算这些点的传输函数的值,并取它们的包络,该包络才是需要的频率特性。
当然,点数取得多一些,该包络才能接近真正的频率特性。
注意:非周期信号的频率特性是w 的连续函数,而周期信号的频率特性是离散谱,它们的计算公式不一样,响应的波形也不一样。
实验内容和步骤1.已知系统用下面差分方程描述:)1()()(-+=n ay n x n y试在95.0=a 和5.0=a 两种情况下用傅立叶变换分析系统的频率特性。
要求写出系统的传输函数,并打印w e H jw ~)(曲线。
MATLAB 代码如下:B=1;A=[1,-0.95];subplot(2,3,3);zplane(B,A);xlabel('实部Re');ylabel('虚部Im');title('y(n)=x(n)+0.95y(n-1)传输函数零、极点分布');grid on[H,w]=freqz(B,A,'whole');subplot(2,3,1);plot(w/pi,abs(H),'linewidth',2);grid on;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性');axis([0,2,0,2.5]);subplot(2,3,2);plot(w/pi,angle(H),'linewidth',2);grid on;axis([-0.1,2.1,-1.5,1.5]);xlabel('\omega/\pi');ylabel('\phi(\omega)');title('相频响应特性');B=1;A=[1,0.5];subplot(2,3,6);zplane(B,A);xlabel('实部Re');ylabel('虚部Im');title('y(n)=x(n)-0.5y(n-1)传输函数零、极点分布');grid on[H,w]=freqz(B,A,'whole');subplot(2,3,4);plot(w/pi,abs(H),'linewidth',2);grid on;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性');axis([0,2,0,2.5]);subplot(2,3,5);plot(w/pi,angle(H),'linewidth',2);grid on;axis([-0.1,2.1,-1.5,1.5]);xlabel('\omega/\pi');ylabel('\phi(\omega)');title('相频响应特性');运行结果如下图所示:2.已知两系统分别用下面差分方程描述:)1()()(1-+=n x n x n y)1()()(2--=n x n x n y 试分别写出它们的传输函数,并分别打印w e H jw ~)(曲线。
傅里叶变换光谱的相关实验与研究的开题报告

傅里叶变换光谱的相关实验与研究的开题报告一、选题背景及意义傅里叶变换(Fourier Transform, FT)是一种非常重要的数学工具,广泛应用于物理、化学、工程等多个领域。
傅里叶变换光谱是一种应用傅里叶变换法分析光学信号的方法,通过将光信号变换到频域来对光谱特性进行研究,具有很高的精度和准确度,被广泛应用于分析光子晶体、表面增强拉曼光谱等研究领域,对于物质的结构和性质的研究具有重要的科学意义。
二、研究目的本研究旨在通过对FT光谱的相关实验研究,深入探究FT光谱的理论基础和应用方法,构建有效的FT光谱分析模型,提高FT光谱分析的准确性和可靠性。
三、研究内容和方法1. 研究FT光谱的原理和数学基础,了解FT光谱的基本特点和应用范围。
2. 确定研究对象,选取多个实验样品进行FT光谱分析实验。
3. 利用傅里叶变换仪器对实验样品进行扫描,得到相应的原始数据。
4. 进行数据处理,通过MATLAB等软件进行数据分析,绘制出样品的频率谱,分析频谱的特点,找到不同样品的差异所在。
5. 通过对不同样品的分析,构建出可靠的FT光谱分析模型,提高分析准确度和稳定性。
四、研究预期结果与意义1. 通过实验研究,深入了解FT光谱的理论基础和应用方法,为FT光谱分析提供科学和实践基础。
2. 构建有效的FT光谱分析模型,提高FT光谱分析的准确性和可靠性,为光学研究领域提供有益的实践经验。
3. 对比分析不同样品的频率谱,寻找不同样品的差异所在,有助于提高对物质结构和性质的认识和探究,具有较高的学术价值。
五、参考文献1. Hasan, S. H., Ashraf, S. A., & Begum, R. (2019). Fourier transform infrared (FTIR) spectroscopy: Techniques and applications in geomorphology. Journal of molecular structure, 1192, 270-277.2. Luo, Y., Wen, Y., Chen, X., Zou, J., & Tang, H. (2019). Quantitative analysis of multiple components by near-infrared spectroscopy based on spectrum non-linearity optimization and partial least squares regression. Talanta, 205, 120154.3. Ribeiro, D. S., Ren, T., Arnaud, C., Ruas, A., & He, L. (2019). Fourier transform infrared spectroscopy (FTIR) as a tool to investigate lipids complexity in biomaterials. Materials Science and Engineering: C, 104, 110090.。
数字实验报告2离散傅立叶变换

陕西科技大学实验报告班级 学号 姓名 实验组别实验日期 室温 报告日期 成绩 实验名称:离散时间傅里叶变换 一、实验目的1.复习离散时间傅立叶正反变换2.复习DTFT 的两个重要特性3.复习DTFT 的其它特性4.离散LTI 系统的频率响应5.采样及重构信号 二、实验原理1、信号的离散时间傅立叶变换(DTFT )2、DTFT 的两个重要特性周期性:离散时间傅立叶变换是w 的周期函数,其周期为2π。
对称性:对于实值的X(n),是共扼对称的。
即实部为偶对称,虚部为奇对称。
3、DTFT 的其他特性线性; 时移:共扼: 折叠: 卷积: 乘法: 能量:4、LTI 系统的频率响应5、模拟信号的采样与重构采样定理重构: 步骤如下dwe e X n x e n x eX jwn jwn n jwnjw⎰∑-∞-∞=-==πππ)(21)()()()]([)]([)]()([2121n x bF n x aF n bx n ax F +=+∑∞-∞=-=n jwnjwen h eH )()((a )先把样本集转换成一个加权脉冲串列(b )再将此脉冲串列通过一个带宽为F 的低通滤波器进行滤波。
以上两个步骤可用插值公式来描述: 三、实验内容1.求信号的离散时间傅立叶变换并分析其周期性和对称性; 给定正弦信号x(t)=2*cos(2*pi*10*t),fs=100HZ,求其DTFT 。
close all clcf=10;T=1/f;w=-10:0.2:10; t1=0:0.0001:1;t2=0:0.01:1; n1=-2;n2=8;n0=0;n=n1:0.01:n2; x5=[n>=0.01]; x1=2*cos(2*f*pi*t1); x2=2*cos(2*f*pi*t2); x3=(exp(-j).^(t2'*w)); x4=x2*x3;subplot(2,2,1);plot(t1,x1);axis([0 1 1.1*min(x2) 1.1*max(x2)]); xlabel('x(n)'); ylabel('x(n)'); title('原信号x1'); xlabel('t');ylabel('x1'); subplot(2,2,3);stem(t2,x2); axis([0 1 1.*min(x2) 1.1*max(x2)]); title('原信号采样结果x2'); xlabel('t');ylabel('x2');∑∞-∞=-=n a Ts t Fs c n x t x )]([sin )()(subplot(2,2,2);stem(n,x5);axis([0 1 1.*min(x5) 1.1*max(x5)]); xlabel('n');ylabel('x2'); title('采样函数x2'); subplot(2,2,4);stem(t2,x4);axis([0 1 -0.2+1.1*min(x4) 1.1*max(x4)]); xlabel('t');ylabel('x4');0.10.20.3-2-1012tx 1原信号x10.050.10.150.20.25-2-1012原信号采样结果x2tx 20.020.040.060.0800.51nx 2采样函数x20.10.20.30.511.52tx 42.用以下两个有限长序列来验证DTFT 的线性、卷积和共轭特性; x1(n)=[1 2 3 4 5 6 7 8 9 10 11 12];x2(n)=R10(n) 1)线性:w=linspace(-8,8,10000); nx1=[0:11]; nx2=[0:9];x1=[1 2 3 4 5 6 7 8 9 10 11 12]; x2=[1 1 1 1 1 1 1 1 1 1 ];x3=[x2,zeros(1,(length(x1)-length(x2)))]; x4=2*x1+3*x3;X1=x1*exp(-1i*nx1'*w);X3=x3*exp(-1i*nx1'*w); X4=x4*exp(-1i*nx1'*w);subplot(5,3,4),stem(nx1,x1),axis([-1,13,0,20]); subplot(5,3,2),stem(nx2,x2),axis([-1,13,0,5]); subplot(5,3,3),stem(nx1,x4),axis([-1,13,0,26]); subplot(5,3,1),plot(w,abs(X1)); subplot(5,3,7),plot(w,abs(X1)); subplot(5,3,10),plot(w,abs(X1)); subplot(5,3,13),plot(w,abs(X1)); subplot(5,3,5),plot(w,abs(X3)); subplot(5,3,8),plot(w,abs(X3)); subplot(5,3,11),plot(w,abs(X3)); subplot(5,3,14),plot(w,abs(X3)); subplot(5,3,6),plot(w,abs(X4)); subplot(5,3,9),plot(w,angle(X4)); subplot(5,3,12),plot(w,angle(X4)); subplot(5,3,15),plot(w,angle(X4));2)卷积性: close all510010201231246851015-10010050100-10010050100-10010050100-1010050100-8-6-4-2020510-6-4-20246-8-6-4246-8-6-42468-100100100200-6-5-4-3-2-101-5-4.5-4-202-4-202-4-202clcnx1=0:11; nx2=0:9; nx3=0:20;w=linspace(-8,8,40); %w=[-8,8]分10000份 x1=[1 2 3 4 5 6 7 8 9 10 11 12]; x2=[1 1 1 1 1 1 1 1 1 1]; x3=conv(x1,x2);% x1卷积x2x4=x1*exp(-j*nx1'*w);% x1频率特性 x5=x2*exp(-j*nx2'*w);% x2频率特性 x6=x3*exp(-j*nx3'*w);% x1卷积x2频率特性 x7=x4.*x5;subplot(2,2,1),stem(nx1,x1),axis([-1,15,0,15]),title('x1'); subplot(2,2,2),stem(nx2,x2),axis([-1,15,0,5]),title('x2'); subplot(2,1,2),stem(nx3,x3),axis([-1,25,0,80]);title('x1卷积x2结果x3');figure,subplot(2,2,1),stem(x4,'filled'),title('x1的DTFT 结果x4'); subplot(2,2,2),stem(x5,'filled'),title('x2的DTFT 结果x5'); subplot(2,2,3),stem(x6,'filled'),title('x3的DTFT 结果x6'); subplot(2,2,4),stem(x7,'filled'),title('x4的DTFT 结果x7'); figure,subplot(3,2,1),stem(w,abs(x6)), ylabel('幅度'),title('x1卷积x2的DTFT');subplot(4,2,3),stem(w,angle(x6)),ylabel('相位') subplot(4,2,5),stem(w,real(x6)),ylabel('实部') subplot(4,2,7),stem(w,imag(x6)),ylabel('虚部')subplot(4,2,2),stem(w,abs(x7)), title('x1与x2的DTFT 的乘积'); subplot(4,2,4),stem(w,angle(x7)); subplot(4,2,6),stem(w,real(x7)); subplot(4,2,8),stem(w,imag(x7))5101551015x15101512345x251015202520406080x1卷积x2结果x33)共轭性x1n=[1 2 3 4 5 6 7 8 9 10 11 12];w=-10:10; N1=length(x1n); n1=0:N1-1; x1=real(x1n); x2=imag(x1n); x2n=x1-j*x2;X1=x2n*(exp(-j).^(n1'*w)); X2=x1n*(exp(j).^(n1'*w)); x3=real(X2); x4=imag(X2); X2=x3-j*x4;figure,subplot(211);stem(w,X1,'.');title('x1n 共轭的DTFT'); subplot(212);stem(w,X2,'.');title('x1n 的DTFT 取共轭且反折')-10-55100200400600800幅度x1卷积x2的DTFT-10-5510-505相位-10-5510-2000200实部-6-4-22-600-400-2000200虚部-6-4-2020500x1与x2的DTFT 的乘积-10-50510-505-4-2024-2000200-6-4-202-600-400-200020010203040-5050x1的DT FT 结果x481012141618-2024x2的DT FT 结果x5101520-2000200400x3的DT FT 结果x6102030-1000100200x4的DT FT 结果x7-3-2-101220406080x1n 共轭的DTFT-7-6-5-4-3-2-10123-50050100x1n 的DTFT 取共轭且反折3.求LTI 系统的频率响应给定系统H(Z)=B(Z)/A(Z),A=[0.98777 -0.31183 0.0256];B=[0.98997 0.989 0.98997],求系统的幅频响应和相频响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目离散傅里叶变换的分析与研究
姓名XX
专业电子信息工程
学号XXXXXXXXXX
学院物理与电子信息学院
指导教师XXX
淮北师范大学教务处制
一、本课题研究现状及可行性分析
离散傅里叶变换,其实质是有限长序列傅立叶变换的有限点离散采样,从而实现了频域离散化,使数字信号处理可以在频域采用数值运算的方法进行,这样就大大增加了数字信号处理的灵活性。更为重要的是,离散傅里叶变换有多种快速算法,统称为快速傅里叶变换,从而使信号的实时处理和设备的简化得以实现。所以说,离散傅立叶变换不仅在理论上有重要意义,而且在各种信号的处理中亦起着核心作用。
离散傅里叶变换在数字通信、语音信号处理、图像处理、功率谱估计、系统分析与仿真、雷达信号处理、光学、医学、地震以及数值分析等各个领域都有着广泛的应用。
目前,我们已具备有关的大量参考文献和基本的原始程序,对本论文的开展不存在根本性的问题,我们的研究方法是可行的。
二、本课题研究的关键问题及解决问题的思路
关键问题:
五、指导教师意见
该生已查阅大量资料以及相关文献,对本课题有一定的理解,解决问题的方法可行,思路清晰,准备充分,同意开题。
指导教师(签名):
2012年月日
六、教研室审核意见
同 意 开 题
教研室主任(签名):
下由学生独立撰写,在毕业论文(设计)开始二周内完成,交指导教师审阅,接受学校和学院抽查。
线性卷积与循环卷积之间的关系,及对信号的频谱分析。并在MATLAB环境下的编程实现。
解决思路:
在理解和掌握线性卷积,循环卷积以及信号频谱分析的基础上,用MATLAB语言编写线性卷积,循环卷积以及频谱分析的设计程序,最后通过仿真结果验证理论的正确性。
三、论文纲要
1绪论
1.1DFT的定义
1.2DFT与傅里叶变换和Z变换的关系
[7]薛年喜.MATLAB在数字信号处理中的应用.北京:清华大学出版社,2004
[8]张德丰.数字信号处理与应用[M].北京:清华大学出版社,2010.1
[9]王永玉,孙衢.数字信号处理及应用-实验教程[M].北京:北京邮电大学出版社,2009
[10]王世一.数字信号处理[M].北京:北京工业学院出版社,1987
[3]楼顺天,李博菡.基于MATLAB的系统分析与设计-信号处理[M].西安:西安电子科技大学出版社,1998
[4]曹戈.MATLAB教程及实训[M].北京:中国电力出版社,2008 [5] 郑君里.信号与系统[M].2版.北京:高等教育出版社,2000
[6]陈怀琛,吴大正,高西全.MATLAB及在电子信息课程中的应用[M].3版.北京:电子工业出版社,2006
2 DFT的基本性质
2.1 线性性质
2.2 循环卷积性质
2.3循环卷积定理
3 DFT的应用
3.1 用DFT计算线性卷积
3.2 用DFT对信号进行谱分析
3.3 用DFT进行谱分析的误差问题
四、主要参考文献
[1]丁玉美,高西全.数字信号处理[M].3版.西安:西安电子科技大学出版社,2008.8
[2]胡广书.数字信号处理-理论、算法与实现[M].北京:清华大学出版社,1998
