5第五章_离散傅里叶变换解析
离散傅里叶变换 DFT
数字信号处理第五章离散傅里叶变换授课教师：胡双红联系QQ：79274544长沙理工大学计算机与通信工程学院DFT:离散傅里叶变换引言DFSDFTDFT性质DFT应用快速算法：FFT引言DTFT对绝对可加序列给出了频域（ω）表示 Z变换对任意序列给出了广义频域（z）表示 特点：变换都是对无限长序列定义的；变换都是连续变量（ω或z ）的函数；用MATLAB实现时必须将序列截断然后在有限点上求表达式。
即DTFT和ZT都不是数值可计算的变换数值可计算的变换DFT方法：通过在频域对DTFT采样获得。
步骤：通过分析周期序列来建立傅里叶级数(DFS)将DFS推广到有限长序列得DFT优点：适合计算机实现的数值可计算的变换缺点：对长序列的数值计算费时多改进方法：快速傅里叶变换（FFT）第一次课5.1 离散傅里叶级数定义MATLAB实例与Z变换和DTFT的关系Z域采样与重建~式中：x解：由题设可得基波周期~~令x周期，⎪⎧±±==−,2,,02N Lk j N N k L π"作出L=5和N=20的周期序列图>> x=[1,1,1,1,1,zeros(1,15)];>> xtilde=x'*ones(1,3);>> xtilde=xtilde(:);>> xtilde=xtilde';>> n=[-20:39];>> stem(n,xtilde)>> axis([-20,39,-0.5,1.5]);>> xlabel('n');ylabel('x(n)');title('周期方波序列')2）对L=5和N=20的MATLAB脚本如下------------------------MATLAB脚本--------------------->> L=5;N=20;k=[-N/2:N/2];% 方波参数>> xn=[ones(1,L),zeros(1,N-L)];% 方波序列x(n) >> Xk=dfs(xn,N);% DFS>> magXk=abs([Xk(N/2+1:N) Xk(1:N/2+1)]);% DFS幅度>> subplot(2,2,1);stem(k,magXk);>> axis([-N/2,N/2,-0.5,0.5]);>> subplot(2,2,1);stem(k,magXk);>> axis([-N/2,N/2,-0.5,5.5]);>> xlabel('k');ylabel('Xtilde(k)');>> title('L=5,N=20 的方波的DFS');3）结论：方波DFS的DFT包络为抽样函数"sinc"函数k=0时幅度为L，函数的零点在N/L的整数倍点 方波持续时间相同时，周期越大，其频谱越密设x(n)是一有限长的序列，长度为N,即：那么它的z 变换和DTFT 为：,01()0,n N x n n ≤≤−⎧=⎨⎩非零其余()()()()∑∑−=−−=−==1010N n jwnjw N n n e n x e X zn x z X 与Z 变换和DTFT 的关系（了解）~现在以周期3）在4）在解：序列x(n)不是周期的，但是有限长的在设x(n)任意序列N−∞1上式表明：单位圆上对X(z)采样，时域将得到一个周期序列，是原序列x(n)和它的无穷多个移位±rN 的副本的线性组合。
离散时间傅里叶变换
X
(e
j
)
sin
N1
sin
1 2
2
连续时间非周期矩形脉冲傅里叶变换： X(j)2sinT1
4. x[n][n]
X(ej) 1
Xej xnejn nejn1
n
n
20
三、离散时间傅里叶变换的收敛性
例5.1，5.2是无限长序列
x[n]a|n|,|a|1; 其傅里叶变换存在。 x[n]anu[n]|,a|1
X * ( e j ) X ( e j )即,X * ( e j ) X ( e j )
因此:
X (ej)X (e j) RX ( e ej) RX ( e e j) X (ej) X (e j) Im X (ej) Im X (e j)
❖ 若 x[n] 是实偶信号,则 x[n]x[n],
x% [n]X(ej)
ak2(k02l) kN l
23
如图P263 Fig5.9:下页
X (e j ) 2 a 0 ( 2 l) 2 a 1 (0 2 l)
l
l
.. .2aN1 ((N1)02l) ,02/N l
如果周期函数中包含连续相继的N次谐波，则有：
X(ej)2k ak(2N k)
调制特性在信息传输中是极其重要的。
一定是以 2 为周期的,因此,频域的冲激应该是周
期性的冲激串:
2（0 2k）
k
对其作反变换有
xn 1 X ej ejnd
2 2
0 ejnd ej0n
2
22
可见, 2（ 02k） F 1 ej0n k
由DFS ,有 ~ xnkNakejk0n,02N
因此,周期信号 ~xn 可表示为DTFT
离散傅里叶变换
c) 频域循环移位定理 若
则
21
3.2.3 循环卷积定理
长度分别为N1和N2的有限长序列x1(n)和x2(n)的N点DFT
分别为： （ N=max［ N1, N2 ］）。
X1(k)=DFT［x1(n)]
X2(k)=DFT［x2(n)］ 如果 则 X(k)=X1(k)· X2(k)
x n IDFT X k x1 m x2 n m N RN n
10
定义： 的主值区间：周期序列 中从n=0到N-1的范围 的主值序列：主值区间上的序列 为叙述方便，将式(3.1.5)该写成
x n N 表示x(n)以N为周期的周期延拓序列，符号((n))N表示n对模
N的余数，即
这里k是商。
11
例如，N=7,
=x((n))7，则有
x 7 x 7 7 x 0 x 8 x 8 7 x 1
类似
Note：对实序列有 X k X N k
DFT x N n X k , 0 k N 1
28
3.2.5 DFT的共轭对称性
1. 有限长共轭对称序列和共轭反对称序列
分别用xep(n)和xop(n) 表示有限长共轭对称序列和共轭反对称
由此对长度为N的序列x(n)，且 x n x n N ，则
X k x n W
n 0 N 1 kn N
的DFS为
x n N W
n 0
N 1
kn N
kn x n WN n 0
N 1
1 N 1 1 N 1 kn kn x n X k WN X k WN N n 0 N n 0
§5-6 离散时间傅里叶变换----DTFT
《信号与系统》
Electronic Technology Teaching & Research Section
二、离散时间傅里叶变换的举例
1、单边指数序列 于是
X (e ) =
jω ∞ n = −∞
x ( n)
a>0 0
1 2 3 45
x ( n) = a n u ( n)
− jω n
a <1
n − jωቤተ መጻሕፍቲ ባይዱn
π
《信号与系统》
Electronic Technology Teaching & Research Section
于是，我们得到一对变换关系：
X ( e ) = DTFT { x ( n )} =
jω − jω n x ( n ) e -------DTFT变换式 ∑ ∞
n = −∞
π
1 jω jω jωn x(n) = IDTFT{X (e )} = X ( e ) e dω -------DTFT反变换式 ∫ 2π −π
5、奇、偶、虚、实性 设
DTFT x ( n ) = x r ( n ) + jx i ( n ) ←⎯ ⎯→ X ( e jω ) = X R ( ω) + jX I ( ω)
= X ( e jω ) e jϕ ( ω )
当x(n)是实序列，即 则
x(n) = x* (n)
X ( e jω ) = X * ( e − jω )
ω
0
π
2π
ω
《信号与系统》
Electronic Technology Teaching & Research Section
DTFT x ( n ) ← ⎯ ⎯→ X ( e jω ) 例题：设
离散时间傅里叶变换
离散时间傅⾥叶变换1. 离散时间傅⾥叶变换的导出针对离散时间⾮周期序列，为了建⽴它的傅⾥叶变换表⽰，我们将采⽤与连续情况下完全类似的步骤进⾏。
考虑某⼀序列x[n]，它具有有限持续期；也就是说，对于某个整数N1和N2，在 −N1⩽以外，x[n]=0。
下图给出了这种类型的⼀个信号。
由这个⾮周期信号可以构成⼀个周期序列\tilde x[n]，使x[n]就是\tilde x[n]的⼀个周期。
随着N的增⼤，x[n]就在⼀个更长的时间间隔内与\tilde x[n]相⼀致。
⽽当N\to \infty，对任意有限时间值n⽽⾔，有\tilde x[n]=x[n]。
现在我们来考虑⼀下\tilde x[n]的傅⾥叶级数表⽰式\tag{1}\tilde x[n] = \sum_{k=(N)}a_ke^{jk{(2\pi/N)}n}\tag{2}a_k = \frac{1}{N} \sum_{n=(N)} \tilde x[n]e^{-jk{(2\pi/N)}n}因为在-N_1 \leqslant N \leqslant N_2区间的⼀个周期上\tilde x[n]=x[n]，因此我们将上式的求和区间就选在这个周期上\tag{3}a_k = \frac{1}{N} \sum_{n=-N_1}^{N_2} x[n]e^{-jk{(2\pi/N)}n} = \frac{1}{N} \sum_{n=-\infty}^{+\infty} x[n]e^{-jk{(2\pi/N)}n}现定义函数\tag{4}X(e^{j\omega})=\sum_{n=-\infty}^{+\infty}x[n]e^{-j\omega n}可见这些系数a_k正⽐于X(e^{j\omega})的各样本值，即\tag{5}a_k = \frac{1}{N}X(e^{jk\omega_0})式中，\omega_0=2\pi/N⽤来记作在频域中的样本间隔。
离散傅里叶变换系数
离散傅里叶变换系数离散傅里叶变换（Discrete Fourier Transform，DFT）是傅里叶变换在离散域上的一种形式。
它广泛应用于信号处理、图像处理、通信等领域。
离散傅里叶变换系数是对原始信号在频域上的表示，常用于分析信号的频谱特性、提取信号中的特征等。
离散傅里叶变换系数的计算可以通过快速傅里叶变换（Fast Fourier Transform，FFT）算法来高效地实现。
下面将介绍离散傅里叶变换系数的相关参考内容。
1. 基本定义：离散傅里叶变换系数可以用复数表示。
设原始信号为长度为N 的离散序列x(n)，其离散傅里叶变换系数为X(k)，则离散傅里叶变换的定义为：X(k) = ∑ [x(n) * e^(-j2πnk/N)]， n=0,1,2,...,N-1, k=0,1,2,...,N-1。
2. 离散傅里叶变换系数的物理意义：离散傅里叶变换系数表示了原始信号在不同频率分量上的能量分布。
离散傅里叶变换系数的模表示信号在该频率上的幅度，相位表示信号在该频率上的相位差。
3. FFT算法：离散傅里叶变换系数的计算可以通过FFT算法来高效地实现。
FFT算法将离散傅里叶变换的计算复杂度从O(N^2)降低到O(NlogN)。
FFT算法的基本思想是将信号分解成序列长度为2的幂次的子序列，然后利用蝶形结构的计算流程递归计算离散傅里叶变换。
4. 离散傅里叶变换系数的性质：离散傅里叶变换系数具有多种性质，包括线性性质、频率平移性质、频率抽样性质、能量守恒性质等。
这些性质可以用于信号处理的分析和计算。
5. 应用领域：离散傅里叶变换系数广泛应用于信号处理、图像处理、通信等领域。
在信号处理中，可以通过计算离散傅里叶变换系数来分析信号的频谱特性，如频率成分、频率间隔等。
在图像处理中，可以通过计算图像的二维离散傅里叶变换系数来进行图像压缩、图像滤波等操作。
在通信中，离散傅里叶变换系数可以用于信号的调制、解调、信道估计等。
离散傅立叶变换
（2）x(n)的4点DFT
X 1 (k ) x(n)W
n 0 3 kn 4
W
n 0
3
kn 4
4, 0,
k 0 k 1, 2, 3
9
（3）x(n)的8点DFT
X 2 (k ) x(n)W8kn W8kn e
n 0 7 3
3 j
2 kn 81610例题 Nhomakorabea图形显示
从图可见，同一 序列不同点数的 DFT是不相同的。 比较可以发现， 对原序列尾部补 零后增加的谱线 只是有规律地插 在频谱的一个周 期内。
11
DFT和Z变换、序列的傅里叶变换的关系
设序列x(n)的长度为N，其Z变换、傅里叶变换和DFT分别为
X ( z ) Z [ x(n)] x(n) z n
X (k ) X ( z) z W k e j 2k / N
N
0≤k≤ N-1 0≤k≤ N-1
X (k ) X (e jw ) w 2k / N
第一式表明，序列x(n)的N点DFT相当于是在x(n)
的z变换的单位圆上进行N点等间隔取样，同时第 一个取样点应取在z= 1处。 第二式说明，X(k)是x(n)的傅里叶变换X(ejω)在区 间[0，2π]上的N点等间隔取样。
m 0
N 1
23
循环卷积定理证明
证明
X (k ) DFT [ x(n)]
kn x1 (m) x2 (( n m)) N RN (n)WN n 0 m 0
N 1 N 1
kn x1 (m) x 2 (( n m)) N WN m 0 n 0
N 1
数字信号处理：离散傅里叶变换(DFT)
X (k ) XX((kkX)))X(XX(z(ez(zzjjjj))))222kk,,k, 200k0,kkkNN--1N1-1 0((33..1(1.3.44.)1k).4) NNN N
2021/8/24
6
3.1 离散傅里叶变换的定义
DFT的物理意义：
(1)x(n)的N点DFT 是x(n)的Z变换在单位
。 j 2 kn 8
解: (1) 设变换区间N=8， 则：n0
N 0
XX(k(k)
77
)
nn00
xx(Xn(n)W()Wk8k)8nkn 3373 eexj 28j(28knnkn)We8jk83nk NnN000
sin(3 k 2 sin kn
80,1,
,
7
(2) 设变换区间N=16， 则 2 k 8
设序列x(n)的长度为N， 其Z变换和DFT分别为：
N 1
X (z) ZT[x(n)] x(n)zn
n0
N 1
X (k) DFT[x(n)] x(n)WNkn
n0
0 k N-1
X (比k较) 上XXX面(((kkkX)二))式X(XX(z(可z(z)z)))得zzzezej2关jeN2Njk2Nke,系k,j,2N式 k00,0kkkNN--N11-10 ((33k..1(1.3.33.)1).3)N
(
j2 k
X
(k)
X(k)
DFT
[=x(Xn~ ()k]
)RNDD(nFF)ST[n[x~x(0~n()n] )RNnN01(n
[0, 2]上的N点
单位圆上的N
等间隔采样
DFT
点等间隔采样
~
X (k ) DFFTT [ x(n)] ZT DFT [x(n)RN (n)] X
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X p (k ) x p (n)W
nk N
e
n 0
4
2 j nk 10
1 e
j
2 5k 10 2 k 10
1 e
j
sin k j 2 k 2 e 5 sin k 10
5.1 离散傅里叶级数
例题5-2：对于周期序列，试证明离散傅里叶级数 只取决于周期序列中任意一个周期内的样值，与 取样的时间序号起点无关。（P17） f p (t ) Fk
X (k )
' p
n1 N 1 mn1
x p (m)W
m n1
mn1
x p (m)W
n1 1 l 0
N 1
mk N
n1 N 1 m N
mk x ( m ) W p N
X (k )
相频特性
2 k k N
0 2 0 k N
e jn e
j 2 kn N
周期序列是在时 间和频率上均为 离散的一类信号
5.1 离散傅里叶级数
例5-1：求所示周期序列的离散傅里叶级数，并画出该 周期序列的幅频特性 周期序列的周期N=10
j 2 10
WN W10 e
离散的周 期序列
Fourier级数 Fourier变换
单位圆的Z变换
频域信号 离散的非 周期序列
连续的非 周期函数 连续的周 期函数 离散的周 期序列
？
适合计算机处理
5.1 离散傅里叶级数 Fourier变换 ？？？ 离散的频谱 Fourier反变换
离散的时 域信号
周期的频谱
周期的时 域信号
5.1 离散傅里叶级数 周期性 e
jk0t F e k
5.1 离散傅里叶级数
周期序列
x p (n) x p (n rN)
Z变换
X p ( z)
n
x p ( n) z
N r
n
r n 0
( n rN ) x ( n rN ) z p
N 1
周期N 趋于无穷大
可任取一个周期
N 1 nk x p (n)WN
e j0Ts
X p (k ) n 0 主值序列
周期N
1 N 1 kn x p (n) X p (k )WN N k 0
5.1 离散傅里叶级数
幅频特性
j p ( k )
X p (k ) X p (k ) e
离散频谱
j
2 kn N
1 x ( n) 2
X (e j )e jn d
t0 T0
t0
f p (t )e jk0t dt
f p (t )
k
jk0t F e k
周期的时域信号－>离散频谱 离散的时域信号 －>周期频谱
WN e
j 2 N
主值区间
[0, N-1]
1 1 e 2 j ( k m) N 1 e N
j 2 ( k m) N N
1 , k m 0 , k m
j 2 ( N 1) n N
e
j
2 0n N
e
j
2 n N
e
j
2 2n N
…
e
5.1 离散傅里叶级数
x p ( n ) 1 (c0 e
N
j 2 0n N
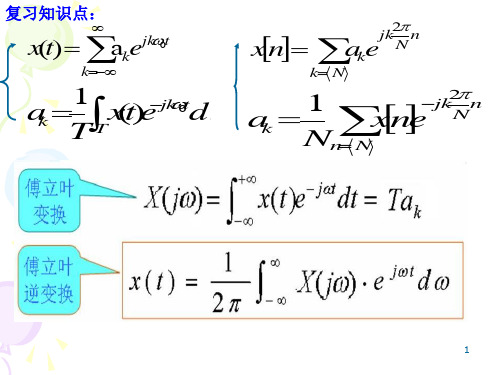
第五章 离散傅里叶变换
•5.1 •5.2 •5.3 •5.4 •5.5 离散傅里叶级数 离散傅立叶变换 离散傅立叶变换的基本性质 DFT与z变换间的关系 各类FT的关系
5.1 离散傅里叶级数 •1 几种傅里叶变换 •2 离散傅立叶级数 •3 周期卷积
X (e j )
n
x ( n )e
X (k )
' p rN n1 N 1 n rN n1
x p (n)W
nk N
X (k )
' p
n1 N 1 mn1
x p (m rN )W
mk N
( m rN ) k N
n1 N 1 mn1
mk Nrk x ( m ) W W p N N
e
j 2 n N
j 2 ( n rN ) N
e
j
2 n N
e
j
2 rN N
e
j
2 n N
的性质
周期为N的周期序列
归一性
正交性
单位圆上的 均匀采样
|e
j
2 n N
2
| 1
2 2
1 N 1 j N kn j N mn 1 N 1 j N ( k m) n e e e N n 0 N n 0
jn
1 x ( n) 2
X (e j )e jn d
jt
jt
1 x(t ) 2
X ( j) x(t )e
dt
d
1 Fk T0
t0 T0
t0
f p (t )e jk0t dt
X ( j)e
f p (t )
k
c1e
j2n N
... c N 1e
j
2 ( N 1) n N )
1 ck e N k 0
N 1 n 0
N 1
2 kn N
e
N 1
jk 0 t
t nTs
e jk0Ts n e
2 mn N
jk
0 2n s
e
1 Fk T0
N 1 n 0
周期N
j
周期N
2 nk N
e jn e
X (e )
j n jn x ( n ) e
j
2 kn N
X p ( k ) x p ( n )e
N 1
1 x p ( n) X p ( k )e N k 0
周期序列的z变换和傅立叶 变换不存在
r
z
N 1 n x ( n ) z p n 0
收敛域不存在
j
X p (e ) x p (n)e
n
jn
5.1 离散傅里叶级数 时域信号
连续的周 期函数 连续的非 周期函数 离散的非 周期序列
j
2 kn N
x p ( n )e
N 1
j
2 mn N
1 ck e k 0 N n 0
N 1
1 [ ck e n0 N k 0
N 1
j
2 kn N
]e
j
2 j ( k m) n N
cm
5.1 离散傅里叶级数 DFS IDFS