离散傅里叶变换和快速傅里叶变换
[理学]离散傅里叶变换及其快速算法
![[理学]离散傅里叶变换及其快速算法](https://img.taocdn.com/s3/m/a4bbbd1b0912a21615792901.png)
非周期序列的离散时间傅里叶变换 (DTFT) /序列的傅里叶变换
• 定义序列x(n)的离散时间傅里叶变换(DTFT)为:
X (e ) DTFT{x(n)}
j n jn x ( n )e
• 序列x(n)的离散时间傅里叶逆变换(IDTFT)为:
x(n) IDTFT{X (e j )} 1 2
按时间抽取的FFT算法
• 设N=2M,M为正整数,如取N=23=8,即离散时间信号为
x(n) {x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7)}
• 按照规则①将序列x(n)分为奇偶两组,一组序号为偶数, 另一组序号为奇数,即
{x(0), x(2), x(4), x(6) | x(1), x(3), x(5), x(7)}
X (e j )e jn d
傅里叶变换对小结
• 傅里叶级数(FS)(时域:连续周期;频域:非周期离散)
1 Xk T
T 2
T 2
x(t )e jk1t dt
x(t )
k
X k e jk1t
k 0, 1, 2,
• 傅里叶变换(FT)(时域:连续非周期;频域:非周期连续)
第三章离散傅里叶变换及其快速计算方法(DFT、FFT)

X (e jw )
(2)Z 变换 -- 提供任意序列的 z 域表示。
n
x( n)e jnw
X (z)
n
x ( n) z n
这两种变换有两个共同特征:
(1)变换适合于无限长序列 (2)它们是连续变量 ω 或 z 的函数
华北电力大学自动化系
3
3.1 问题的提出:可计算性
X (z)
而对于
n
x ( n) z n
n
x ( n) z n
找不到衰减因子使它绝对可和(收敛)。为此,定义新函 数,其 Z 变换:
华北电力大学自动化系
15
DFS 定义:正变换
X ( z)
n
x ( n) z n ~ ( n ) z n x
华北电力大学自动化系
6
3.1 问题的提出:傅里叶变换的四种形式 (3)
2. 周期连续时间信号:傅里叶级数 FS
~ (t ) x X (n 0 )
t T
时域周期频域离散
0
2 T
x(t)
~
n -
X(n 0 )e jn0t
时域连续函数造成频域是非周期的谱。 频域的离散对应时域是周期函数。
X (e jT )
T T
X (e jT )e jnT d
取样定理
n
x(nT )e jnT
1 X ( 0 ) T n
时域的离散化造成频域的周期延拓 时域的非周期对应于频域的连续
华北电力大学自动化系
8
离散傅里叶变换和快速傅里叶变换的区别

离散傅里叶变换和快速傅里叶变换的区别离散傅里叶变换(Discrete Fourier Transform,DFT)和快速傅里叶变换(Fast Fourier Transform,FFT)都是数字信号处理中常用的算法,用于将时域信号转换为频域信号。
虽然它们都是傅里叶变换的变种,但它们之间有很大的区别。
DFT是一种直接计算傅里叶变换的方法,它将N个时域采样点转换为N个频域采样点。
DFT的计算复杂度为O(N^2),因此对于大规模的信号处理任务来说,计算时间会非常长。
而FFT是一种基于分治思想的算法,它将DFT的计算复杂度降低到O(NlogN),因此计算速度非常快,特别适合于大规模信号处理任务。
DFT和FFT的计算方式也有所不同。
DFT的计算公式为:X[k] = sum(x[n] * exp(-j*2*pi*k*n/N))其中,x[n]表示时域采样点,X[k]表示频域采样点,N表示采样点数,k和n分别表示频域和时域的索引。
这个公式需要进行N^2次复数乘法和加法运算,因此计算复杂度很高。
FFT的计算方式则是将DFT的计算过程分解为多个子问题,然后递归地求解这些子问题。
具体来说,FFT将N个采样点分为两个子序列,分别进行DFT计算,然后将它们合并起来得到整个序列的DFT结果。
这个过程可以递归地进行下去,直到只剩下一个采样点为止。
由于FFT采用了分治思想,它的计算复杂度为O(NlogN),比DFT快得多。
DFT和FFT的应用场景也有所不同。
由于DFT的计算复杂度较高,因此它适合于小规模的信号处理任务,例如音频信号的处理。
而FFT则适合于大规模的信号处理任务,例如图像处理和视频处理。
此外,FFT还可以用于信号压缩、滤波和频域分析等领域。
离散傅里叶变换和快速傅里叶变换虽然都是傅里叶变换的变种,但它们之间有很大的区别。
DFT是一种直接计算傅里叶变换的方法,计算复杂度较高,适合于小规模的信号处理任务;而FFT是一种基于分治思想的算法,计算速度非常快,适合于大规模的信号处理任务。
数字图像处理中的常用变换

一、离散傅里叶变换1.离散傅里叶变换的特点离散傅里叶变换(DFT),是连续傅里叶变换在时域和频域上都离散的形式,将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。
在形式上,变换两端(时域和频域上)的序列是有限长的,而实际上这两组序列都应当被认为是离散周期信号的主值序列。
即使对无限长的离散信号作DFT,也应当将其看作经过周期延拓成为周期信号再作变换。
在实际应用中通常采用快速傅里叶变换以高效计算DFT。
DFT将空域变换到频域,很容易了解到图像的各空间频域的成分。
DFT的应用十分广泛,如:图像的特征提取、空间频率域滤波、图像恢复和纹理分析等。
2.离散傅里叶变换的性质1)线性性质2)比例性质3)可分离性4)平移性质5)图像中心化6)周期性7)共轭对称性8)旋转不变性9)卷积定理10)平均值二、离散余弦变换1.离散余弦变换简介为了快速有效地对图像进行处理和分析,常通过正交变换将图像变换到频域,利用频域的特有性质进行处理。
传统的正交变换多是复变换,运算量大,不易实时处理。
随着数字图像处理技术的发展,出现了以离散余弦变换(DCT)为代表的一大类正弦型实变换,均具有快速算法。
目前DCT变换在数据压缩,图像分析,信号的稀疏表示等方面有着广泛的应用。
由于其变换矩阵的基向量很近似于托普利兹(Toeplitz )矩阵的特征向量,而托普利兹矩阵又体现了人类语言及图像信号的相关特性,因此常被认为是对语音和图像信号的最佳变换。
对给定长度为N 的输入序列f(x),它的DCT 变换定义为:⎪⎭⎫ ⎝⎛+⨯=∑-=102)12(cos )()(2)(N x N x x f u C N u F μπ式中:1,,1,0u -=N ,式中的)(u C 的满足:⎪⎩⎪⎨⎧==其它1021)(u u C在数字图像处理中,通常使用二维DCT 变换,正变换为:⎪⎪⎭⎫ ⎝⎛++⨯=∑∑-=-=10102)12(cos 2)12(cos ),()()(2),(N x N y N v y N u x y x f v C u C N v u F ππ 其逆变换IDCT 为:⎪⎭⎫ ⎝⎛++⨯=∑∑-=-=10102)12(cos 2)12(cos ),()()(2),(N u N v N v y N u x v u F v C u C N y x f ππ 式中:1,,1,0u -=N ,1,,1,0v -=N 。
离散傅里叶变换及其快速算法
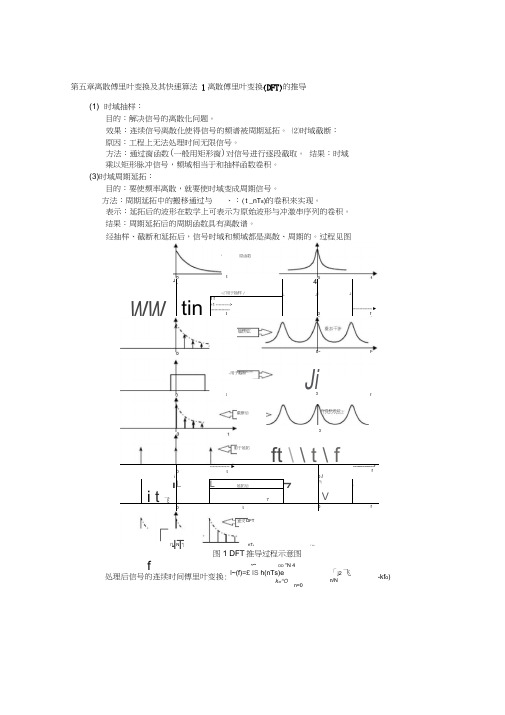
第五章离散傅里叶变换及其快速算法 1离散傅里叶变换(DFT)的推导(1) 时域抽样:目的:解决信号的离散化问题。
效果:连续信号离散化使得信号的频谱被周期延拓。
⑵时域截断: 原因:工程上无法处理时间无限信号。
方法:通过窗函数(一般用矩形窗)对信号进行逐段截取。
结果:时域乘以矩形脉冲信号,频域相当于和抽样函数卷积。
(3)时域周期延拓:目的:要使频率离散,就要使时域变成周期信号。
方法:周期延拓中的搬移通过与 、:(t _nT s )的卷积来实现。
表示:延拓后的波形在数学上可表示为原始波形与冲激串序列的卷积。
结果:周期延拓后的周期函数具有离散谱。
经抽样、截断和延拓后,信号时域和频域都是离散、周期的。
过程见图抽样后0 fJif-用于截断原函数J L<Z 用于抽样i4LJI Ji WWtin1 f=1 ----------> --------------t-------------- ►fVtt截断后有卷积波纹i------------- ►t0 I------------------ rfJL 」L延拓后7角ii t飞7Vtfft \ \ t \ f定义DFT用于延拓「ITf处理后信号的连续时间傅里叶变换:I'U N *|nT sr 0 N图1 DFT 推导过程示意图〜 oo "N 4l ~(f)=£ IS h(nTs)ek =^O「j2 飞n/Nn=0-kf o )(i) l~(f)是离散函数,仅在离散频率点f二kf o k—处存在冲激,强度为a k,其T o NT s余各点为0。
〜N N 1(ii) H(f)是周期函数,周期为Nf o == 工,每个周期内有N个不同的幅值。
T o NT s T s(iii) 时域的离散时间间隔(或周期)与频域的周期(或离散间隔)互为倒数。
2 DFT及IDFT的定义DFT定义:设hnT s是连续函数h(t)的N个抽样值n=0,1,…,N J,这N个点的宽度为N 的DFT 为:DFT N h(nT s)]=^ h(nT s)e」2邢/N =H —— J (k =0,1,…,N _1)7 l NT s 丿IDFT定义:设H 上是连续频率函数H(f)的N个抽样值k =0,1,…,N J,这N个点(NT s 丿的宽度为N的IDFT为:DFT N1 H k丄7 H L e」2「nk/N厶nTs , (k =0,1,…,N —1)|L Ns N k 卫NT se^Rk/N称为N点DFT的变换核函数,e j2 flk/N称为N点IDFT的变换核函数。
离散傅里叶变换的基本性质

x(5 )
A(6 )
W
0 N
x(3 )
A(7 )
x(7 )
W
0 N
A(0 )
A(1 )
A(2 )
W
0 N
A(3 )
W
2 N
A(4 )
A(5 )
A(6 )
W
0 N
A(7 )
W
2 N
A(0 )
A(1 )
A(2 )
A(3 )
A(4 )
W
0 N
A(5 )
W
1 N
A(6 )
W
2 N
A(7 )
W
3 N
N点DIT―FFT运算流图(N=8)
A(5 )
A(6 )
W
0 N
A(7 )
W
2 N
A(0 )
A(1 )
A(2 )
A(3 )
A(4 )
W
0 N
A(5 )
W
1 N
A(6 )
W
2 N
A(7 )
W
3 N
N点DIT―FFT运算流图(N=8)
A(0 ) X(0 ) X(1 ) X(2 ) X(3 ) X(4 ) X(5 ) X(6 )
A(7 ) X(7 )
m N
WN 2
WNm
2. 时域抽取法基2FFT基本原理 FFT算法基本上分为两大类:
时域抽取法FFT(Decimation In Time FFT,简称DITFFT)和频域抽取法FFT(Decimation In Frequency FFT,简 称DIF―FFT)。下面先介绍DIF―FFT算法。
设序列x(n)的长度为N,且满足
N 2M , M 为自然数
离散傅里叶变换及其快速算法
ak 也是以 N周期的周期序列,满足 ak
~ X (k ) Nak
ak 。令 ln
(3.5)
将式(3.4)代入,得
N 1 j kn ~ ~ N X ( k ) x ( n )e n 0 2
k
(3.6)
~ X (k ) 式中, 是以N为周期的周期序列,称为
~ x (n) 的离散傅里叶级数,用DFS表示。
~(k ), N 相位为 幅度为 X
~ arg[ X (k )]
。
基波分量的频率为 2 N ,幅度为
~ 为arg[ X (1)]
~ X (1) N
,相位
。
x ( n ) 以 N 8 为周期 n) 【例3-1】设 x(n) R4 (,将
进行周期延拓,得到周期序列 幅频特性。
~ x ( n)
2016-12-8
解:根据定义求解
14 12 e 8e
j
j
2 k 6
10e
j
j
2 2k 6 j 2 5k 6
2 3k 6
6e
2 4k 6
10e
X (0) 60 X (3) 0
X (1) 9 j 3 3 X (4) 3 j 3
X (2) 3 j 3 X (5) 9 j 3 3
x 3(n )
当k取奇数( k=2m+1 ,m=0,1,…, N/4-1 )时
N n(2 m 1) X 1(2m 1) x 1(n ) x 1 n 4 W N 2 n 0 N 4 1 N n mn x 1(n ) x 1 n W W N N 4 4 n 0 2
第二章 离散傅里叶变换及其快速算法
表示这个顺序时,它正好是“码位倒置”的顺序 。例如,原来的自然顺序应是 x(1)的地方,现在 放着 x(4),用二进制码表示这一规律时, 则是在
x(0 0 1)处放着 x(1 0 0), x(0 1 1)处放着 x(1 1 0)。
表 码位倒置顺序
自然顺序
二进码表示
FFT算法的基本思想:
考察DFT与IDFT的运算发现,利用以下两个特性可减少运
算量: 1)系数
wNnk
j 2 nk
e N 是一个周期函数,它的周期性和对称
性可用来改进运算,提高计算效率。
例 w N n(N k)w N k(N n)w N nk
又如 wNN/2 1,
因此
w(kN/2) N
wN k
k , , ,N
X (k N 2 ) G k W N k H k ,
k 0 ,1 , N 1 2
依此类推,G(k)和H(k)可以继续分下去,这种按时间抽 取算法是在输入序列分成越来越小的子序列上执行DFT
运算,最后再合成为N点的DFT。
蝶形信号流图
将G(k)和H(k) 合成X(k)运算可归结为:
2、按时间抽取的FFT(N点DFT运算的分解) 先从一个特殊情况开始,假定N是2的整数次方,
N=2M,M:正整数
首先将序列x(n)分解为两组,一组为偶数项,一组为奇 数项,
x(x2(r2 r)1) x1 x(2 r()r)
r0,, 1,N-/12
将DFT运算也相应分为两组:
N1
x(k)DF x(T n) x(n)w N nk
N/21
X(2r) a(n)WNn/r2 n0 N/21
X(2r1) b2(n)WNn/2r n0
第四章 离散傅里叶变换及其快速算法
离散 连续
周期延拓 非周期
4.1 离散傅里叶变换的定义
kn X (k ) DFT [ x(n)] x(n)WN , n 0 N 1 N 1 n 0 2 kn N
= x ( n )e
j
k=0, 1, , N-1
X ( k )WN kn k 0 N 1
1 x(n) IDFT [ X (k )] N 1 N
4 N
x D1X N
W N ( N 1 ) 2 ( N 1 ) WN W N ( N 1 )( N 1 ) 1
1
D
1 N
W N 2 ( N 1 )
1 DN N
dftmtx(N) 函数产生N×N的DFT矩阵DN conj(dftmtx(N))/N 函数产生N×N的IDFT矩阵DN-1
二、 圆周移位性质
1. 序列的圆周移位 x(n)的圆周移位定义为
y(n)=x((n+m))N RN(n) 其过程为: 1)、将x(n)以N为周期进行周期延拓得x((n))N 2)、将x((n))N左移m位,得x((n+m))N 3)、取其主值序列x((n+m))N RN(n) 循环移位过程如图所示
WNN 1
2 WN ( N 1)
WNN 1 2 WN ( N 1) ( WN N 1) ( N 1)
DFT
IDFT矩阵形式为
1 1 1 W 1 N 1 D 1 1 W N 2 N N 1 W N ( N 1 ) 1 W N 2 W
0 n N `1 0 k N `1
DFT 则: x1 (n) x2 (n) X1 ( K ) X 2 ( K )
FFT变换相关公式IFFT变换(FFT逆变换)
FFT变换相关公式IFFT变换(FFT逆变换)离散傅里叶变换(Discrete Fourier Transform, DFT)是信号处理中的一种重要技术,用于将一个离散序列(如时域信号)转换为频域表示。
而逆离散傅里叶变换(Inverse Discrete Fourier Transform, IDFT)则是将频域信号转换回时域表示。
在信号处理中,常用的FFT算法(快速傅里叶变换)是对DFT的一种高效实现,能够大大加快计算速度。
FFT算法利用了信号的周期性和对称性,将DFT的计算量从O(n^2)降低到O(nlogn),其中n是信号的长度。
下面介绍一些与FFT和IFFT相关的公式和性质。
1.DFT公式:离散傅里叶变换的公式如下:X[k] = Σ(x[n] * exp(-i * 2π * k * n / N))其中,X[k]是频域信号的第k个频率分量,x[n]是时域信号的第n个采样点,N是信号的长度。
2.IDFT公式:逆离散傅里叶变换的公式如下:x[n] = (1/N) * Σ(X[k] * exp(i * 2π * k * n / N))其中,x[n]是逆变换后的时域信号,X[k]是频域信号的第k个频率分量,N是信号的长度。
3.FFT算法公式:FFT算法是一种将DFT计算量降低的方法,公式如下:X[k] = Σ(x[n] * W^(-kn))其中,W = exp(-i * 2π / N)是旋转因子,n和k分别表示时域和频域的索引。
4.IFFT算法公式:IFFT算法是FFT的逆变换,可以将频域信号转换为时域信号,公式如下:x[n] = (1/N) * Σ(X[k] * W^(kn))其中,W = exp(i * 2π / N)是旋转因子,n和k分别表示时域和频域的索引。
5.FFT和IFFT的性质:-线性性质:FFT和IFFT都满足线性性质,即对于多个信号的线性组合,其FFT和IFFT等于各自信号的FFT和IFFT的线性组合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告课程名称: 信号分析与处理 指导老师: 成绩:__________________实验名称:离散傅里叶变换和快速傅里叶变换 实验类型: 基础实验 同组学生姓名:第二次实验 离散傅里叶变换和快速傅里叶变换一、实验目的1.1掌握离散傅里叶变换(DFT )的原理和实现;1.2掌握快速傅里叶变换(FFT )的原理和实现,掌握用FFT 对连续信号和离散信号进行谱分析的方法。
1.3 会用Matlab 软件进行以上练习。
二、实验原理2.1关于DFT 的相关知识序列x (n )的离散事件傅里叶变换(DTFT )表示为nj n j en x e X Ω-∞-∞=Ω∑=)()(,如果x (n )为因果有限长序列,n =0,1,...,N-1,则x (n )的DTFT 表示为n j N n j e n x e X Ω--=Ω∑=1)()(,x (n )的离散傅里叶变换(DFT )表达式为)1,...,1,0()()(21-==--=∑N k en x k X nk NjN n π,序列的N 点DFT 是序列DTFT 在频率区间[0,2π]上的N 点灯间隔采样,采样间隔为2π/N 。
通过DFT ,可以完成由一组有限个信号采样值x (n )直接计算得到一组有限个频谱采样值X (k )。
X (k )的幅度谱为)()()(22k X k X k X I R +=,其中下标R 和I 分别表示取实部、虚部的运算。
X (k )的相位谱为)()(arctan)(k X k X k R I =ϕ。
离散傅里叶反变换(IDFT )定义为)1,...,1,0()(1)(21-==∑-=N n e k X N n x nk Nj N n π。
2.2关于FFT 的相关知识快速傅里叶变换(FFT )是DFT 的快速算法,并不是一个新的映射。
FFT 利用了n Nj eπ2-函数的周期性和对称性以及一些特殊值来减少DFT 的运算量,可使DFT 的运算量下降几个数量级,从而使数字信号处装订线理的速度大大提高。
若信号是连续信号,用FFT 进行谱分析时,首先必须对信号进行采样,使之变成离散信号,然后就可以用FFT 来对连续信号进行谱分析。
为了满足采样定理,一般在采样之前要设置一个抗混叠低通滤波器,且抗混叠滤波器的截止频率不得高于与采样频率的一半。
比较DFT 和IDFT 的定义,两者的区别仅在于指数因子的指数部分的符号差异和幅度尺度变换,因此可用FFT 算法来计算IDFT 。
三、实验内容与相关分析(共6道)说明:为了便于老师查看,现将各题的内容写在这里——题目按照3.1、3.2、...、3.6排列。
每道题包含如下内容:题干、解答(思路、M 文件源代码、命令窗口中的运行及其结果)、分析。
其中“命令窗口中的运行及其结果”按照小题顺序排列,各小题包含命令与结果(图形或者序列)。
3.1 求有限长离散时间信号x (n )的离散时间..傅里叶变换(DTFT )X (e j Ω)并绘图。
(1)已知⎩⎨⎧≤≤-=其他0221)(n n x ;(2)已知1002)(≤≤=n n x n。
【解答】思路:这是DTFT 的变换,按照定义编写DTFT 的M 文件即可。
考虑到自变量Ω是连续的,为了方便计算机计算,计算时只取三个周期[-2π,4π]中均匀的1000个点用于绘图。
理论计算的各序列DTFT 表达式,请见本题的分析。
M 文件源代码(我的Matlab 源文件不支持中文注释,抱歉): function DTFT(n1,n2,x)%This is a DTFT function for my experiment of Signal Processing & Analysis. w=0:2*pi/1000:2*pi;%Define the bracket of omega for plotting. X=zeros(size(w));%Define the initial values of X. for i=n1:n2X=X+x(i-n1+1)*exp((-1)*j*w*i);%It is the definition of DTFT. endAmp=abs(X);%Acquire the amplification.Phs=angle(X);%Acquire the phase angle (radian). subplot(1,2,1);plot(w,Amp,'r'); xlabel('\Omega');ylabel('Amplification');hold on ; %Plot amplification on the left. subplot(1,2,2);plot(w,Phs,'b');xlabel('\Omega');ylabel('Phase Angle (radian)');hold off ; %Plot phase angle on the right. end命令窗口中的运行及其结果(理论计算的各序列DTFT 表达式,请见本题的分析): 第(1)小题>> n=(-2:2); >> x=1.^n;>> DTFT(-2,2,x);-5051000.511.522.533.544.55ΩA m p l i f i c a t i on-50510-4-3-2-101234ΩP h a s e A n g l e (r a d i a n )第(2)小题>> n=(0:10); >> x=2.^n;>> DTFT(0,10,x);-55106008001000120014001600180020002200ΩA m p l i f i c a t i on-50510-4-3-2-101234ΩP h a s e A n g l e (r a d i a n )【分析】对于第(1)小题,由于序列x(n)只在有限区间(-2,-1,-,1,2)上为1,所以是离散非周期的信号。
它的幅度频谱相应地应该是周期连续信号。
事实上,我们可计算出它的表达式:()Ω-Ω-Ω-Ω-Ω-=Ω-∞+-∞=Ω---=Ω⇒--===Ω∑∑j j j j j n nj n n j X n x X e1e 1)(e 1e 1e e e )()(55222,可见幅度频谱拥有主极大图3.1.1在[-2π,4π]范围内3个周期的幅度谱和相位谱(弧度制)图3.1.2在[-2π,4π]范围内3个周期的幅度谱和相位谱(弧度制)和次极大,两个主极大间有|5-1|=4个极小,即有3个次级大。
而对于它的相位频谱,则是周期性地在-π、0、π之间震荡。
对于第(2)小题,由于是离散非周期的信号。
它的幅度频谱相应地应该是周期连续信号。
而它的表达式:()Ω-Ω-Ω-=Ω-+∞-∞=Ω--≈Ω⇒--===Ω∑∑j j j n nj n nj X n x X e212)(e 21e 212ee)()(11111110,因此主极大之间只有|0-1|=1个极小,不存在次级大。
而对于它的相位频谱,则是在一个长为2π的周期内有|11-1|=10次振荡。
而由DTFT 的定义可知,频谱都是以2π为周期向两边无限延伸的。
由于DTFT 是连续谱,对于计算机处理来说特别困难,因此我们才需要离散信号的频谱也离散,由此构造出DFT (以及为加速计算DFT 的FFT )。
3.2已知有限长序列x (n )={8,7,9,5,1,7,9,5},试分别采用DFT 和FFT 求其离散傅里叶变换X (k )的幅度、相位图。
【解答】思路:按照定义编写M 文件即可。
M 文件源代码: i) DFT 函数:function DFT(N,x)%This is a DFT function for my experiment of Signal Processing & Analysis. k=(0:N-1);%Define variable k for DFT.X=zeros(size(k));%Define the initial valves of X. for i=0:N-1X=X+x(i+1)*exp((-1)*j*2*k*pi/N*i);%It is the definition of DFT. endAmp=abs(X);%Acquire the amplification.Phs=angle(X);%Acquire the phase angle (radian). subplot(1,2,1);stem(k,Amp,'.',’MarkerSize ’,18); xlabel('k');ylabel('Amplification');hold on ; %Plot amplification on the left. subplot(1,2,2);stem(k,Phs,'*');xlabel('k');ylabel('Phase Angle (radian)');hold off ; %Plot phase angle on the right. endii) 基2-FFT 函数function myFFT(N,x)%This is a base-2 FFT function. lov=(0:N-1); j1=0;for i=1:N %indexed addressing if i<j1+1temp=x(j1+1); x(j1+1)=x(i); x(i)=temp; endk=N/2;while k<=j1j1=j1-k;k=k/2;endj1=j1+k;enddigit=0;k=N;while k>1digit=digit+1;k=k/2;endn=N/2;% Now we start the "butterfly-shaped" process.for mu=1:digitdif=2^(mu-1);%Differnce between the indexes of the target variables.idx=1;for i=1:nidx1=idx;idx2=1;for j1=1:N/(2*n)r=(idx2-1)*2^(digit-mu);wn=exp(j*(-2)*pi*r/N);%It is the "circulating coefficients".temp=x(idx);x(idx)=temp+x(idx+dif)*wn;x(idx+dif)=temp-x(idx+dif)*wn;idx=idx+1;idx2=idx2+1;endidx=idx1+2*dif;endn=n/2;endAmp=abs(x);%Acquire the amplification.Phs=angle(x);%Acquire the phase angle (radian).subplot(1,2,1);stem(lov,Amp,'.',’MarkerSize’,18);xlabel('FFT k');ylabel('FFT Amplification');hold on;%Plot the amplification.subplot(1,2,2);stem(lov,Phs,'*');xlabel('FFT k');ylabel('FFT Phase Angle (radian)');hold off; end命令窗口中的运行及其结果:DFT :>> x=[8,7,9,5,1,7,9,5]; >> DFT(8,x);24680102030405060kA m p l i f i c a t i o n02468-3-2-1123kP h a s e A n g l e (r a d i a n )FFT : >> x=[8,7,9,5,1,7,9,5]; >> myFFT(8,x);24680102030405060FFT kF F T A m p l i f i c a t i o n02468-3-2-1123FFT kF F T P h a s e A n g l e (r a d i a n )【分析】DFT 是离散信号、离散频谱之间的映射。
