圆小结与复习课件
最新:人教版九年级上册数学第24章《圆》小结与复习第2课时

(2)举例说明如何计算扇形面积
在半径为R的圆中,因为圆心角是360°的扇形
面积就是圆面积 S R2,所以圆心角是1°的扇
形面积是
R2 360
。这样,在半径为R的圆中,圆心角为
n°的扇形面积S的扇计形 算公n3式6R是02:
1°的扇形面积是 1 R2 360
1°
° n° n°圆心角的扇形的面积 n R2 360
三、选择题:
下A、列三命角题形正外确心的到是三(边C距离)相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆
四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,
则这个三角形的面积为_3_0_c_m__.
相信自己我能行
1P.为如A图B,上6⊙一O动的点半,则径点OAPA 到=1圆0c心mO,的弦最A短B=距16离cm,
.
∵直线l是⊙O的切线,切 点为A
∟
O.
∴ OA⊥ l
A
l
典例精析
【例2】.在Rt△ABC中,∠B=90°,∠A的平分线交 BC于D,以D为圆心,DB长为半径作⊙D.
试说明:AC是⊙D的切线.
过D点作DF ⊥AC于F点,
然后证明DF等于圆D的半
F
径BD
【例3】、如图,AB在⊙O的直径,点D在AB的延长 线上,且BD=OB,点C在⊙O上,∠CAB=30°. (1)CD是⊙O的切线吗?说明你的理由; (2)AC=_____,请给出合理的解释.
B D
C
· E
A
五、 切线 (1) 切线的识别方法: 1.与圆有一个公共点的直线。 2.圆心到直线的距离等于圆的半径的直线是
人教版九年级数学上册第24章《圆》知识小结与复习

A
A.140°B.135°C.130°D.125°
DF
∠BOC=90°+ 1∠A 2
R
E
BM
Q
O
G
P
NC
3、边长分别为3,4,5的三角形的内切圆半径与外 接圆半径的比为( )
A.1∶5 B.2∶5 C.3∶5 D.4∶5
4.已知△ABC,AC=12,BC=5,AB=13。则 △ABC的外接圆半径为 。内切圆半径____ 5. 正三角形的边长为a,它的内切圆和外接圆的半 径分别是______, ____
O1
AM
O
B
如图,在矩形ABCD中,AB=20cm,BC=4cm,点 ⊙p从A开始折线A—B—C—D以4cm/秒的速度 移动,点⊙Q从C开始沿CD边以1cm/秒的速度移 动,如果点⊙P, ⊙Q分别从A,C同时出发,当其中一 点到达D时,另一点也随之停止运动,设运动的时 间t(秒) 如果⊙P和⊙Q的半径都是2cm,那么t 为何值时, ⊙P和⊙Q外切?
(2)若C△ABC= 36, S△ABC=18,则r内=_1____; (3)若BE=3,CE=2, △ABC的周长为18,则AB=_7___;
A
D
8
F
4
o
B
6E
C
1 S △ABC= 2 C △ABC·r内
2.△ABC中, ∠A=70°,⊙O截△ABC三条边所得的
弦长相等.则 ∠BOC=__D__.
3.两圆相切,圆心距为10cm,其中一个圆的半径为 6cm,则另一个圆的半径为_____.
4. 已知圆O1与圆O 2的半径分别为12和2,圆心O1的 坐标为(0,8),圆心O2 的坐标为(-6,0),则两圆的位置 关系是______.
第24章 圆的小结与复习
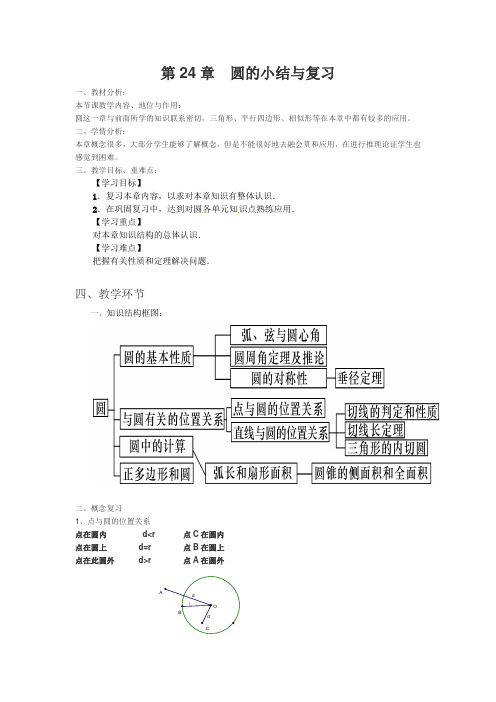
第24章 圆的小结与复习一、教材分析: 本节课教学内容、地位与作用; 圆这一章与前面所学的知识联系密切,三角形、平行四边形、相似形等在本章中都有较多的应用。
二、学情分析:本章概念很多,大部分学生能够了解概念,但是不能很好地去融会贯和应用,在进行推理论证学生也感觉到困难。
三、教学目标、重难点;【学习目标】1.复习本章内容,以求对本章知识有整体认识. 2.在巩固复习中,达到对圆各单元知识点熟练应用.【学习重点】对本章知识结构的总体认识.【学习难点】把握有关性质和定理解决问题.四、教学环节一、知识结构框图:二、概念复习 1、点与圆的位置关系点在圆内 d<r 点C 在圆内点在圆上 d=r 点B 在圆上点在此圆外 d>r 点A 在圆外2、直线与圆的位置关系•直线与圆相离d>r 无交点•直线与圆相切d=r 有一个交点•直线与圆相交d<r 有两个交点3、垂径定理垂径定理:垂直于弦的直径平分这条弦并且平分这条弦所对的两条弧推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;以上共3个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB是直径②AB⊥CD ③CE=DE ④⑤①②③④⑤或①③②④⑤或……4、圆心角定理•圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等此定理也称1推3定理,即上述四个结论中,只要知道其中的1个相等,则可以推出其它的3个结论也即:①∠AOB=∠DOE ②AB=DE ③OC=OF ④①②③④或②①③④……即:∠AOB=2∠ACB5、圆周角定理的推论:推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
即:∠C=∠D推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径即:在⊙O中,∵AB是直径或∵∠C=90°∴∠C=90°∴AB是直径6、圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角.即:在⊙O中,∵四边形ABCD是内接四边形,∴∠C+∠BAD=180°,B+∠D=180°,∠DAE=∠C7、切线的性质与判定定理(1)性质定理:圆的切线垂直于过切点的半径(如上图)∵MN是切线∴MN⊥OA(2)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线两个条件:过半径外端且垂直半径,二者缺一不可即:∵MN⊥OA且MN过半径OA外端∴MN是⊙O的切线切线长定理切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,圆心与这一点的连线平分两条切线的夹角. 即:∵PA 、PB 是的两条切线,∴PA=PB ,PO 平分∠BPA8、圆内接正多边形的计算(1)正三角形1::2弧长、扇形面积公式(1)弧长公式: (2)扇形面积公式:三、随堂训练 学生把通过“自学互研”得出的结论展示出来,并将疑难问题板演到黑板上由学生进行讨论,老师最后再予以点评。
九年级数学上册第二十四章章圆小结与复习课件

∵∠P+∠AOB=180°,∠P=70°, ∴∠DOE=55°.
(2)若PA=4 cm,求△PDE的周长.
(2)∵⊙O分别切PA、PB、DE于A、B、C, ∴AD=CD,BE=CE. ∴△PDE的周长=PD+PE+DE =PD+AD+BE+PE=2PA=8(cm)
考点四 圆中的计算问题
例5 如图,四边形OABC为菱形,点B、C在以点O为圆 心的圆上, OA=1,∠AOC=120°,∠1=∠2,则扇形 OEF的面积?
三、 圆的基本性质 1. 圆的对称性 圆是轴对称图形,它的任意一条___直__径__所在的直
线都是它的对称轴.
2. 有关圆心角、弧、弦的性质. (1)在同圆中,如果圆心角相等,那么 它们所对的弧相等,所对的弦也相等.
圆心角 相等
(2)在同圆或等圆中,如果两个圆心角、 弧
弦
两条弧和两条弦中有一组量相等,那么 相等
3.与切线相关的定理 (1)判定定理:经过圆的半径的外端且垂直于这 条半径的直线是圆的切线.
(2)性质定理:圆的切线垂直于经过切点的半径.
(3)切线长定理:经过圆外一点所画的圆的两条 切线,它们的切线长相等.这一点和圆心的连线 平分这两条切线的夹角.
四、 圆中的计算问题 1.弧长公式
n R
半径为R的圆中,n°圆心角所对的弧长l=__18_0_____. 2.扇形面积公式 半径为R,圆心角为n°的扇形面积S= _n_36_R0_2或____12_l_R__. 3.弓形面积公式
n
(2)正n边形的边长a,半径R,边心距r之间的关系
R2 r2 (a)2. 2
(3)边长a,边心距r的正n边形的面积为
S 1 nar 1 lr. 22
其中l为正n边形的周长.
高中数学必修二第四章小结与复习课件(1)

P1(x1 , y1 , z1 )
O
P2 (x2 , y2 , z2 )
x
y
本章易错点
1.在使用圆的一般方程 x2+y2+Dx+Ey+F=0时, 必须确保 D2+E2-4F否>则0 ,方程不表示圆. 2.判断圆与圆的位置关系时,不能只看交点个数, 两圆有一个公共点,可能是外切,也可能是内切; 两圆没有公共点,可能是外离,也可能是内含.
2.联立两圆方程,看截得解得个数.
△<0
n=0
两个圆相离
△=0
n=1
两个圆相切
△>0
n=2
两个圆相交
4.2.3直线与圆的方程的应用
坐标法解决平面几何问题的“三步曲” • 第一步:建系,几何问题代数化; • 第二步:解决代数问题; • 第三步:还原结论.
4.3空间直角坐标系
4.3.1空间直角坐标系
3.建立直角坐标系,满足建系规则才能建立右手坐 标系.
第四章 圆与方程
4.1圆的方程 4.2直线、圆的位置关系 4.3空间直角坐标系
学法指点
1.要学会根据题目条件,恰当选择圆方程情势: ①若知道或涉及圆心和半径,我们一般采用圆的
标准方程较简单. ②若已知三点求圆的方程,我们常常采用圆的一
般方程用待定系数法求解.
2. 直线与圆的位置关系可以通过公共 点的个数来来判断,但圆与圆的位置关系 不能只通过公共点的个数来判断.
高考热点
1.用圆的标准方程和一般方程解决问题.
(x a)2 (y b) 2 r2 x2+y2+Dx+Ey+F=0 (D2+E2-4F>0)
y
M r
A
O
x
2.直线与圆的位置关系,及圆与圆位置关系 的判定.
苏教版小学五年级数学下册第六单元《圆》课件
课堂小结
通过这节课的学习活动,你有什么收获?
1.圆是由曲线围成的封闭图形。
2.用圆规画圆时,针尖固定的一点是圆心, 连接圆心和圆上任意一点的线段是半径, 通过圆心并且两端都在圆上的线段是直径。
课堂小结
3.圆有无数条直径和半径。在同圆或 等圆中,直径的长度是半径的2倍, 半径的长度是直径的一半,用字母表 示为d=2r或r= d 。
钝角 120°
练一练
3.一个圆被分成了三部分(如下图)。你能 比较这三个扇形的大小吗?
最小
最大
课 堂 检 测 (教材91页第11题) 1.在钟表上分别表示分针从12起,走5分钟、15分
钟和30分钟所经过的部分。
扇形
课 堂 检 测 (教材91页第12题) 2.每个圆里的涂色部分和空白部分都可以看作什
探究新知
比较 3 个车轮 的直径和周长, 你有什么发现?
车轮的直径越长, 周长就越长。
探 究 新 知 知识点2:圆周率的意义及圆的周长公式
如右图, 在正方形内画一 个最大的圆。 你知道正方 形的周长是圆直径的几倍吗? 在圆内再画一个正六边形, 六边形的顶点都在圆上, 六 边形的周长是圆直径的几倍?
3.14×66=207.24(厘米) 3.14×61=191.54(厘米) 3.14×56=175.84(厘米)
试一试
答:26英寸车轮的周长大约是207.24厘米; 24英寸车轮的周长大约是191.54厘米; 22英寸车轮的周长大约是175.84厘米。
练一练
一个圆形喷水池的半径是14米。它的周长是
圆的位置和( 圆心 )有关。 同一个圆中,直径和半径的关系为d 2r 或 r d
2
圆是轴对称图形,有(无数条)对称轴。
第24章 圆的复习-九年级数学上册教学课件(人教版)

原 所示,则这个小圆孔的宽口AB的长度为 8 mm.
理
C
精
炼
O
8mm
A
B
提
D
升
与圆有关的概念
典 1.圆:平面内到定点的距离等于定长的所有点组成的图形.
例 2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
原 4.劣弧:小于半圆周的圆弧.
理 5.优弧:大于半圆周的圆弧.
炼 【注意】(1)三角形的外心是三角形三边的垂直平分线的交点.
(2)一个三角形的外接圆是唯一的.
提
(3)三角形的内心是三角形三条角平分线的交点.
升
(4)一个三角形的内切圆是唯一的.
点与圆的位置关系
典 1.在△ABC中,∠C=90º,AC=1,BC=2,M是AB的中点,以点C为圆 例 心,1为半径作⊙C,则( C )
原 2.垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦, 理 并且平分这条弦所对的两条弧;
精 3.垂径定理的推论:平分弧的直径垂直平分这条弧所对的弦. 炼
提 升
圆的基本性质
典 1.圆的对称性: 例 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
原 2.有关圆心角、弧、弦的性质:
理
在同圆或等圆中,如果两个圆心角、
° 精 炼
提 升
典 6.如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点 例 E.若BC=BE.求证:△ADE是等腰三角形.
原 理
精 炼
提 升
典 7.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 例 (1)若∠CBD=39º,求∠BAD的度数; 原 (2)求证:∠1=∠2. 理
五年级下册数学课件 圆复习(共3个课时)苏教版 - 副本

圆 练习十三
3.
(6,4)
(9,2)
(12,3)
(3)把圆O3先向左平移9格,再向上平移2格,画出平移后 的图形,并标出圆心。
返回
圆 练习十三
3.
(6,4) (9,2)
(12,3)
圆的位置与什么 圆的位置与圆
有关?
心有关。
返回
圆 练习十三
4.(1)指出右边圆里的线段哪一条是直径。
d
直径是经过圆心 的线段。
随着数学的发展,特别是计算机的问世,圆周 率的精确度被算得越来越高。现在,人们已经能够 把圆周率精确到小数点后数万亿位。
返回
圆 练习十三
课堂小结
这节课你们都学会了哪些知识?
圆的周长大小和什么有关? 圆的周长和直径、半径的长度有关。 要求圆的周长,就要知道圆的直径或半径。
返回
圆 练习十三
课后作业
补充习题: 对应练习
答:这条小路的面积是113.04平方米。
返回
圆 练习十三
7.右图中正方形的面积是8平方厘米, 你能算出黄色部分的面积吗?
8 × 3.14=25.12(平方厘米) 25.12÷4×3
= 6.28 ×3 = 18.84(平方厘米) 答:黄色部分的面积是18.84平方厘米。
返回
圆 练习十三
课堂小结
这节课你们都学会了哪些知识?
4.一个圆形花圃的周长是50.24米,里 面种植了3种不同的鲜花(如右图)。 先估计每种鲜花种植面积分别占几分之 几,再算出它们大约各有多少平方米?
200.96×1 = 50.24(平方米)
4
200.96× 1 = 100.48(平方米)
2
答:玫瑰和百合的种植面积大约是50.24平方米, 牡丹的种植面积大约是100.48平方米。
