(新人教版)2019版高中数学 第一章 导数及其应用滚动训练二 新人教A版选修2-2【重点推荐】【精品推荐】
高中数学 第一章 导数及其应用 1.3 导数在研究函数中的运用同步练习(含解析)新人教A版选修2-2

高中数学第一章导数及其应用1.3 导数在研究函数中的运用同步练习(含解析)新人教A版选修2-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第一章导数及其应用1.3 导数在研究函数中的运用同步练习(含解析)新人教A版选修2-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第一章导数及其应用1.3 导数在研究函数中的运用同步练习(含解析)新人教A 版选修2-2的全部内容。
1.3导数在研究函数中的运用1。
曲线f (x )=x ㏑x 在点x =1处的切线方程是( )A . y=2x +2B .y=2x -2C .y=x —1D .y=x +1答案:C解析:解答:根据导数的几何意义求出函数f (x )在x =1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式即可解:y=x ln x , y '=1×ln+x •1x=1+ln x , y '=1又当x =1时y=0,∴切线方程为y=x -1即x —y-1=0,故选:C分析:此题主要考查导数的计算,以及利用导数研究曲线上某点切线方程,属于基础题 2.曲线y=2xx -在点(1,-1)处的切线方程为 A .y=x -2 B .y=—3x +2 C .y=2x —3 D .y= —2x +1 答案:D解析:解答:根据题意 ,由于曲线y=2x x -,则可知其导数2222(2)(2)x x y x x ---'==--,故当x =1时,则可知导数值为—2,则由点斜式方程可知为y= —2x +1,选D.分析:主要是考查了导数在研究曲线的切线方程中的运用,属于基础题. 3. 函数21ln 2y x x =-的单调递减区间为( ) A.(—1,1] B.(0,1] C 。
2018-2019版高中数学 第一章 导数及其应用滚动训练一 新人教A版选修2-2

第一章导数及其应用滚动训练一(§1.1~§1.2)一、选择题1.自变量x从x0变化到x1时,函数值的增量与相应自变量的增量之比是函数( ) A.从x0到x1的平均变化率B.在x=x1处的变化率C.在x=x1处的变化量D.在区间[x0,x1]上的导数考点平均变化率题点函数的平均变化率答案 A解析ΔyΔx=f(x1)-f(x0)x1-x0表示函数从x0到x1的平均变化率.2.下列求导结果正确的是( )A.(a-x2)′=1-2x B.(2x3)′=3xC.(cos 60°)′=-sin 60° D.[ln(2x)]′=12x 考点导数公式的应用题点导数公式的应用答案 B解析根据题意,依次分析选项:对于A,(a-x2)′=a′-(x2)′=-2x,故A错误;对于B,(2x3)′=(322x)′=2×32×12x=3x,故B正确;对于C,(cos 60°)′=0,故C错误;对于D,[ln(2x)]′=(2x)′12x=1x,故D错误.故选B.3.函数y=x(1-ax)2(a>0),且y′|x=2=5,则实数a的值为( )A.13B.0C.1 D.2 考点导数乘除法则及运算题点 导数乘除法则及运算 答案 C解析 y ′=(1-ax )2+x [(1-ax )2]′ =(1-ax )2+x [2(1-ax )(-a )] =(1-ax )2-2ax (1-ax ), 由y ′|x =2=(1-2a )2-4a (1-2a ) =12a 2-8a +1=5(a >0), 解得a =1.4.曲线y =ln x 在点M 处的切线过原点,则该切线的斜率为( ) A .1 B .e C .-1eD.1e考点 导数公式的应用 题点 导数公式的应用 答案 D解析 设M (x 0,ln x 0), 由y =ln x 得y ′=1x,所以切线斜率k =0=|x x y'=1x 0,所以切线方程为y -ln x 0=1x 0(x -x 0).由题意得0-ln x 0=1x 0(0-x 0)=-1,即ln x 0=1,所以x 0=e. 所以k =1x 0=1e,故选D.5.已知函数f (x )=a sin x +bx 3+1(a ,b ∈R ),f ′(x )为f (x )的导函数,则f (2 016)+f (-2 016)+f ′(2 017)-f ′(-2 017)等于( ) A .2 017 B .2 016 C .2D .0考点 导数的加减法则及运算 题点 导数的加减法则及运算 答案 C解析 函数的导数f ′(x )=a cos x +3bx 2, 则f ′(x )为偶函数,则f ′(2 017)-f ′(-2 017)=f ′(2 017)-f ′(2 017)=0, 由f (x )=a sin x +bx 3+1,得f (2 016)=a sin 2 016+b ·2 0163+1,f (-2 016)=-a sin 2 016-b ·2 0163+1,则f (2 016)+f (-2 016)=2,则f (2 016)+f (-2 016)+f ′(2 017)-f ′(-2 017)=2+0=2,故选C.6.设f (x )=ln(x +1)+x +1+ax +b (a ,b ∈R 且为常数),曲线y =f (x )与直线y =32x 在点(0,0)相切,则a +b 的值为( ) A .-1 B .1 C .0 D .2 答案 A解析 由y =f (x )过点(0,0)得b =-1, ∴f (x )=ln(x +1)+x +1+ax -1, ∴f ′(x )=1x +1+12x +1+a , 又∵曲线y =f (x )与直线y =32x 在点(0,0)相切,即曲线y =f (x )在点(0,0)处切线的斜率为32,∴f ′(0)=32,即1+12+a =32,∴a =0,故a +b =-1,选A.7.已知函数f (x )及其导数f ′(x ),若存在x 0使得f (x 0)=f ′(x 0),则称x 0是f (x )的一个“巧值点”.给出四个函数:①f (x )=x 2,②f (x )=e -x,③f (x )=ln x ,④f (x )=tan x ,其中有“巧值点”的函数的个数是( ) A .1 B .2 C .3D .4考点 导数公式的应用 题点 导数公式的应用 答案 B解析 根据题意,依次分析所给的函数:①若f (x )=x 2,则f ′(x )=2x ,由x 2=2x ,得x =0或x =2,这个方程显然有解,①符合要求;②若f (x )=e -x,则f ′(x )=-e -x,即e -x=-e -x,此方程无解,②不符合要求; ③f (x )=ln x ,则f ′(x )=1x ,若ln x =1x,利用数形结合可知该方程存在实数解,③符合要求;④f (x )=tan x ,则f ′(x )=1cos 2x,即sin x cos x =1,变形得sin 2x =2,无解,④不符合要求,故选B.8.若函数f (x )=-1be ax (a >0,b >0)的图象在x =0处的切线与圆x 2+y 2=1相切,则a +b 的最大值为( ) A .4 B .2 2 C .2D. 2考点 简单复合函数的导数题点 简单复合函数的导数的综合应用 答案 D解析 函数的导数为f ′(x )=-1be ax·a ,所以f ′(0)=-1b e 0·a =-ab,即在x =0处的切线斜率k =-a b, 又f (0)=-1b e 0=-1b,所以切点坐标为⎝ ⎛⎭⎪⎫0,-1b ,所以切线方程为y +1b =-abx ,即ax +by +1=0.圆心到直线ax +by +1=0的距离d =1a 2+b 2=1,即a 2+b 2=1,所以a 2+b 2=1≥2ab ,即0<ab ≤12.又a 2+b 2=(a +b )2-2ab =1, 所以(a +b )2=2ab +1≤1+1=2, 即a +b ≤2, 当且仅当a =b =22时等号成立, 所以a +b 的最大值是2,故选D. 二、填空题9.已知函数f (x )=mxm -n的导数为f ′(x )=8x 3,则m n=________.考点 常数、幂函数、指数函数、对数函数的导数 题点 常数、幂函数的导数答案 14解析 ∵函数f (x )=mxm -n的导数为f ′(x )=m (m -n )x m -n -1,∴m (m -n )=8且m -n -1=3,解得m =2,n =-2, 由此可得m n =2-2=14.10.若某物体做运动方程为s =(1-t )2(位移单位为m ,时间单位为s)的直线运动,则其在t =1.2 s 时的瞬时速度v 为________ m/s. 考点 导数的几何意义的应用 题点 导数的物理意义 答案 0.4解析 ∵s =t 2-2t +1,∴s ′=2t -2, ∴v =s ′|t =1.2=2×1.2-2=0.4(m/s).11.函数f (x )=x (x -1)(x -2)(x -3)(x -4)的导数为f ′(x ),则f ′(1)=________. 考点 导数的乘除法则及运算 题点 导数的乘除法则及运算 答案 -6解析 ∵f (x )=x (x -1)(x -2)(x -3)(x -4), 令g (x )=x (x -2)(x -3)(x -4), 则f (x )=(x -1)g (x )∴f ′(x )=(x -1)′g (x )+(x -1)g ′(x ) =g (x )+(x -1)g ′(x ),则f ′(1)=g (1)+(1-1)g ′(1)=g (1), ∵g (1)=1×(1-2)(1-3)(1-4)=-6, ∴f ′(1)=g (1)=-6.12.若点P 是曲线y =x 2-ln x 上任意一点,则点P 到直线y =x -2的最小距离为________. 考点 导数公式的应用 题点 导数公式的应用 答案2解析 令y ′=2x -1x =1,得x =1⎝ ⎛⎭⎪⎫x =-12舍去,故当点P 坐标为(1,1)时,它到已知直线的距离最小,最小距离d =|1-1-2|2= 2.三、解答题13.已知a>0,f(x)=ax2-2x+1+ln(x+1),l是曲线y=f(x)在点P(0,f(0))处的切线,求切线l的方程.考点求函数在某点处的切线方程题点求函数在某点处的切线方程解∵f(x)=ax2-2x+1+ln(x+1),f(0)=1,∴f′(x)=2ax-2+1x+1,∴f′(0)=-1,∴切点P的坐标为(0,1),l的斜率为-1,∴切线l的方程为x+y-1=0.四、探究与拓展14.已知函数f(x)=cos x+e-x+x2 016,令f1(x)=f′(x),f2(x)=f1′(x),f3(x)=f2′(x),…,f n+1(x)=f n′(x),则f2 017(x)等于( )A.-sin x+e-x B.cos x-e-xC.-sin x-e-x D.-cos x+e-x考点导数公式的应用题点导数公式的应用答案 C解析f1(x)=f′(x)=-sin x-e-x+2 016x2 015,f2(x)=f1′(x)=-cos x+e-x+2 016×2 015×x2 014,f3(x)=f2′(x)=sin x-e-x+2 016×2 015×2 014x2 013,f4(x)=f3′(x)=cos x+e-x+2 016×2 015×2 014×2 013x2 012,…,∴f2 016(x)=f′2 015(x)=cos x+e-x+2 016×2 015×2 014×2 013× (1)∴f2 017(x)=-sin x-e-x,故选C.15.已知函数f(x)=x3-3x及曲线y=f(x)上一点P(1,-2),过点P作直线l.(1)若直线l与曲线y=f(x)相切于点P,求直线l的方程;(2)若直线l与曲线y=f(x)相切,且切点异于点P,求直线l的方程.考点求函数过某点的切线方程题点求函数过某点的切线方程解(1)由f(x)=x3-3x,得f′(x)=3x2-3.过点P且以P(1,-2)为切点的直线l的斜率为f′(1)=0,故所求直线l的方程为y=-2.(2)设过点P(1,-2)的直线l与曲线y=f(x)相切于点(x0,x30-3x0).由f′(x0)=3x20-3,得直线l的方程为y-(x30-3x0)=(3x20-3)(x-x0).又直线l过点P(1,-2),所以-2-(x 30-3x 0)=(3x 20-3)(1-x 0), 即(x 0-1)2(x 0+2)=3(x 20-1)(x 0-1), 解得x 0=1(舍去)或x 0=-12,故直线l 的斜率k =-94,故直线l 的方程为y -(-2)=-94(x -1),即9x +4y -1=0.。
【2019版新教材】高中数学A版必修第一册第一章全章节教案教学设计+课后练习及答案(名师推荐精编版)

【新教材】人教统编版高中数学A版必修第一册第一章教案教学设计+课后练习及答案1.1 《集合的概念》教案教材分析集合概念及其基本理论,称为集合论,是近、现代数学的一个重要的基础.许多重要的数学分支,都是建立在集合理论的基础上.此外,集合理论的应用也变得更加广泛.教学目标【知识与能力目标】1.通过实例,了解集合的含义,体会元素与集合的属于关系;2.知道常用数集及其专用记号;3.了解集合中元素的确定性、互异性、无序性;4.会用集合语言表示有关数学对象;5.培养学生抽象概括的能力.【过程与方法目标】1.让学生经历从集合实例中抽象概括出集合共同特征的过程,感知集合的含义.2.让学生归纳整理本节所学知识.【情感态度价值观目标】使学生感受学习集合的必要性和重要性,增加学生对数学学习的兴趣.教学重难点【教学重点】集合的含义与表示方法.【教学难点】对待不同问题,表示法的恰当选择.课前准备学生通过预习,自主学习、思考、交流、讨论和概括,从而更好地完成本节课的教学目标.教学过程(一)创设情景,揭示课题请分析以下几个实例:1.正整数1,2,3,;2.中国古典四大名著;3.2018足球世界杯参赛队伍;4.《水浒》中梁山108 好汉;5.到线段两端距离相等的点.在这里,集合是我们常用的一个词语,我们感兴趣的是问题中某些特定对象的总体,而不是个别的对象,为此,我们将学习一个新的概念——集合(宣布课题),即是一些研究对象的总体.(二)研探新知1.集合的有关概念(1)一般地,我们把研究对象统称为元素(element),把一些元素组成的总体叫做集合(set)(简称为集).思考:上述5 个实例能否构成集合?如果是集合,那么它的元素分别是什么?练习1:下列指定的对象,是否能构成一个集合?①很小的数②不超过30 的非负实数③直角坐标平面的横坐标与纵坐标相等的点④ 的近似值⑤高一年级优秀的学生⑥所有无理数⑦大于2 的整数⑧正三角形全体(2)关于集合的元素的特征(a)确定性:设A一个给定的集合,对于一个具体对象a,则a或者是集合A 的元素,或者不是集合 A 的元素,两种情况必有一种且只有一种成立.(b)互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素.一元素.(c)无序性:集合中的元素是没有顺序关系的,即只要构成两个集合的元素一样,我们称这两个集合是相等的,跟顺序无关.(3)思考1:列举一些集合例子和不能构成集合的例子,对学生的例子予以讨论、点评,进而讲解下面的问题.答案:(a)把3-11内的每一个偶数作为元数,这些偶数全体就构成一个集合.(b)不能组成集合,因为组成它的元素是不确定的.( 4)元素与集合的关系;(a)如果a是集合A的元素,就说a属于(belongto) A,记作a € A(b)如果a不是集合A的元素,就说a不属于(not belong to) A,记作a A例如:A表示方程x2=1的解. 2 A, 1CA( 5)集合的表示方法我们可以用自然语言来描述一个集合,但这将给我们带来很多不便,除此之外还常用列举法和描述法来表示集合.(a)列举法:把集合中的元素一一列举出来,并用花括号”。
高中数学第一章导数及其应用本章整合新人教A版选修2_2【含答案】
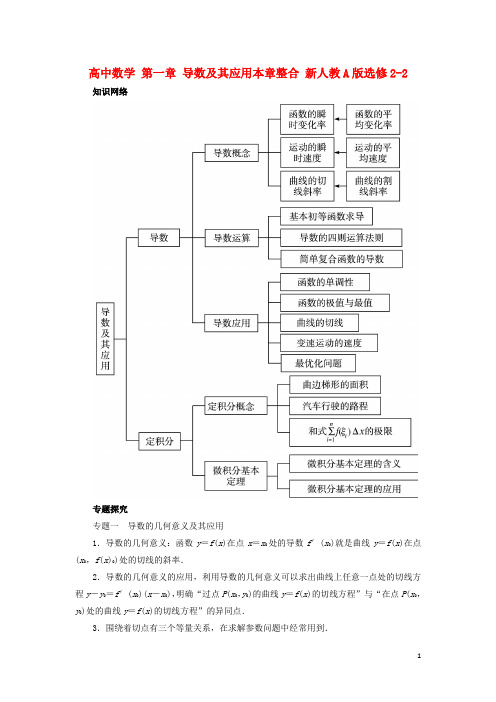
高中数学第一章导数及其应用本章整合新人教A版选修2-2 知识网络专题探究专题一导数的几何意义及其应用1.导数的几何意义:函数y=f(x)在点x=x0处的导数f′(x0)就是曲线y=f(x)在点(x0,f(x)0)处的切线的斜率.2.导数的几何意义的应用,利用导数的几何意义可以求出曲线上任意一点处的切线方程y-y0=f′(x0)(x-x0),明确“过点P(x0,y0)的曲线y=f(x)的切线方程”与“在点P(x0,y0)处的曲线y=f(x)的切线方程”的异同点.3.围绕着切点有三个等量关系,在求解参数问题中经常用到.【例1】已知曲线y =13x 3+43.(1)求曲线在点P (2,4)处的切线方程; (2)求曲线过点P (2,4)的切线方程; (3)求斜率为4的曲线的切线方程.提示:切点坐标→切线斜率→点斜式求切线方程 解:(1)∵P (2,4)在曲线y =13x 3+43上,且y ′=x 2,∴在点P (2,4)处的切线的斜率k =y ′|x =2=4. ∴曲线在点P (2,4)处的切线方程为y -4=4(x -2), 即4x -y -4=0.(2)设曲线y =13x 3+43与过点P (2,4)的切线相切于点A ⎝ ⎛⎭⎪⎫x 0,13x 03+43,则切线的斜率k =0|x x y ='=x 02.∴切线方程为y -⎝ ⎛⎭⎪⎫13x 03+43=x 02(x -x 0),即y =x 02·x -23x 03+43.∵点P (2,4)在切线上, ∴4=2x 02-23x 03+43,即x 03-3x 02+4=0. ∴x 03+x 02-4x 02+4=0.∴x 02(x 0+1)-4(x 0+1)(x 0-1)=0. ∴(x 0+1)(x 0-2)2=0, 解得x 0=-1或x 0=2,故所求的切线方程为4x -y -4=0或x -y +2=0. (3)设切点为(x 0,y 0), 则切线的斜率k =x 20=4, ∴x 0=±2.∴切点为(2,4)或⎝⎛⎭⎪⎫-2,-43.∴斜率为4的曲线的切线方程为y -4=4(x -2)和y +43=4(x +2),即4x -y -4=0和12x -3y +20=0.专题二 利用导数研究函数的单调性借助导数研究函数的单调性,尤其是研究含有ln x ,e x,-x 3等线性函数(或复合函数)的单调性,是近几年高考的一个重点.其特点是导数f ′(x )的符号一般由二次函数来确定;经常同一元二次方程、一元二次不等式结合,融分类讨论、数形结合于一体.【例2】若a ≥-1,求函数f (x )=ax -(a +1)ln(x +1)的单调区间. 解:由已知得函数f (x )的定义域为(-1,+∞),且f ′(x )=ax -1x +1(a ≥-1), (1)当-1≤a ≤0时,f ′(x )<0,函数f (x )在(-1,+∞)上单调递减; (2)当a >0时,由f ′(x )=0,解得x =1a.f ′(x ),f (x )随x 的变化情况如下表:从上表可知,当x ∈⎝ ⎛⎭⎪⎫-1,a 时,f ′(x )<0,函数f (x )在⎝ ⎛⎭⎪⎫-1,a 上单调递减;当x ∈⎝ ⎛⎭⎪⎫1a,+∞时,f ′(x )>0,函数f (x )在⎝ ⎛⎭⎪⎫1a,+∞上单调递增.综上所述,当-1≤a ≤0时,函数f (x )在(-1,+∞)上单调递减.当a >0时,函数f (x )在⎝ ⎛⎭⎪⎫-1,1a 上单调递减,函数f (x )在⎝ ⎛⎭⎪⎫1a ,+∞上单调递增.【例3】若函数f (x )=13x 3-12ax 2+(a -1)x +1在区间(1,4)内为减函数,在区间(6,+∞)上为增函数,试求实数a 的取值范围.解:函数f (x )的导数f ′(x )=x 2-ax +a -1. 令f ′(x )=0,解得x =1或x =a -1.当a -1≤1,即a ≤2时,函数f (x )在(1,+∞)上为增函数,不合题意.当a -1>1,即a >2时,函数f (x )在(-∞,1)上为增函数,在(1,a -1)内为减函数,在(a -1,+∞)上为增函数.依题意当x ∈(1,4)时,f ′(x )<0, 当x ∈(6,+∞)时,f ′(x )>0. 故4≤a -1≤6,即5≤a ≤7. 因此a 的取值范围是[5,7].专题三 利用导数求函数的极值和最值1.极值和最值是两个迥然不同的概念,前者是函数的“局部”性质,而后者是函数的“整体”性质.另函数有极值未必有最值,反之亦然.2.判断函数“极值”是否存在时,务必把握以下原则: (1)确定函数f (x )的定义域; (2)解方程f ′(x )=0的根.(3)检验f ′(x )=0的根的两侧f ′(x )的符号: 若左正右负,则f (x )在此根处取得极大值. 若左负右正,则f (x )在此根处取得极小值.即导数为零点未必是极值点,这一点是解题时的主要失分点,学习时务必引起注意. 3.求函数f (x )在闭区间[a ,b ]上的最大值、最小值的方法与步骤: (1)求f (x )在(a ,b )内的极值;(2)将(1)求得的极值与f (a ),f (b )相比较,其中最大的一个值为最大值,最小的一个值为最小值.【例4】(1)函数f (x )=1x +2x 2+1x 3,求y =f (x )在⎣⎢⎡⎦⎥⎤-4,-12上的最值; (2)若a >0,求g (x )=1x +2x 2+ax3的极值点.解:(1)f ′(x )=-(x +1)(x +3)x, 令f ′(x )>0,得-3<x <-1,令f ′(x )<0,得x <-3,或-1<x <0,或x >0, ∴当x ∈⎣⎢⎡⎦⎥⎤-4,-12时,x ,f ′(x ),f (x )的变化如下表:(2)g ′(x )=-x 2+4x +3ax 4,设u =x 2+4x +3a ,Δ=16-12a , 当a ≥43时,Δ≤0,即g ′(x )≤0,所以y =g (x )没有极值点.当0<a <43时,x 1=-2-4-3a ,x 2=-2+4-3a <0.∴g (x )的递减区间为(-∞,x 1),(x 2,0),递增区间为(x 1,x 2). ∴有两个极值点x 1=-2-4-3a ,x 2=-2+4-3a . 【例5】已知f (x )=x 2+ax -ln x ,a ∈R .(1)若a =0,求函数y =f (x )在点(1,f (x ))处的切线方程; (2)若函数f (x )在[1,2]上是减函数,求实数a 的取值范围;(3)令g (x )=f (x )-x 2,是否存在实数a ,当x ∈(0,e](e 是自然对数的底数)时,函数g (x )的最小值是3,若存在,求出a 的值;若不存在,说明理由.解:(1)当a =0时,f (x )=x 2-ln x , 所以f ′(x )=2x -1x⇒f ′(1)=1,f (1)=1.所以曲线y =f (x )在点(1,f (1))处的切线方程为x -y =0. (2)因为函数在[1,2]上是减函数,所以f ′(x )=2x +a -1x =2x 2+ax -1x≤0在[1,2]上恒成立,令h (x )=2x 2+ax -1,有⎩⎪⎨⎪⎧h (1)≤0,h (2)≤0,得⎩⎪⎨⎪⎧a ≤-1,a ≤-72,得a ≤-72.(3)假设存在实数a ,使g (x )=ax -ln x (x ∈(0,e])有最小值3,g ′(x )=a -1x =ax -1x.①当a ≤0时,g ′(x )<0,所以g (x )在(0,e]上单调递减,g (x )min =g (e)=a e -1=3,a =4e (舍去).②当1a≥e 时,g ′(x )<0在(0,e]上恒成立,所以g (x )在(0,e]上单调递减.g (x )min =g (e)=a e -1=3,a =4e(舍去).③当0<1a <e 时,令g ′(x )<0⇒0<x <1a,所以g (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递减,在⎝ ⎛⎦⎥⎤1a ,e 上单调递增.所以g (x )min =g ⎝ ⎛⎭⎪⎫1a =1+ln a =3,a =e 2,满足条件.综上,存在实数a =e 2,使得当x ∈(0,e]时g (x )有最小值3. 专题四 利用导数证明不等式从近几年高考题看,利用导数证明不等式这一知识点常考到,一般出现在高考题解答题中.利用导数解决不等式问题(如:证明不等式,比较大小等),其实质就是利用求导数的方法研究函数的单调性,而证明不等式(或比较大小)常与函数最值问题有关.因此,解决该类问题通常是构造一个函数,然后考查这个函数的单调性,结合给定的区间和函数在该区间端点的函数值使问题得以求解.其实质是这样的:要证不等式f (x )>g (x ),则构造函数φ(x )=f (x )-g (x ),只需证φ(x )>0即可,由此转化成求φ(x )最小值问题,借助于导数解决.【例6】已知函数f (x )=x 2ex -1-13x 3-x 2. (1)讨论函数f (x )的单调性;(2)设g (x )=23x 3-x 2,试比较f (x )与g (x )的大小.解:(1)f ′(x )=x (x +2)(ex -1-1),由f ′(x )=0得x 1=-2,x 2=0,x 3=1.当-2<x <0或x >1时,f ′(x )>0; 当x <-2或0<x <1时,f ′(x )<0,所以函数f (x )在(-2,0)和(1,+∞)上是单调递增的,在(-∞,-2)和(0,1)上是单调递减的.(2)f (x )-g (x )=x 2ex -1-x 3=x 2(ex -1-x ).因为对任意实数x 总有x 2≥0, 所以设h (x )=ex -1-x .h ′(x )=e x -1-1,由h ′(x )=0得x =1,则当x <1时,h ′(x )<0,即函数h (x )在(-∞,1)上单调递减,因此当x <1时,h (x )>h (1)=0.当x >1时,h ′(x )>0,即函数h (x )在(1,+∞)上单调递增,因此当x >1时,h (x )>h (1)=0.当x =1时,h (1)=0.所以对任意实数x 都有h (x )≥0,即f (x )-g (x )≥0,故对任意实数x ,恒有f (x )≥g (x ). 专题五 导数的应用 解决优化问题的步骤(1)首先要分析问题中各个数量之间的关系,建立适当的函数模型,并确定函数的定义域.(2)其次要通过研究相应函数的性质,如单调性、极值与最值,提出优化方案,使问题得以解决,在这个过程中,导数是一个有力的工具.(3)最后验证数学问题的解是否满足实际意义.【例7】某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格x (单位:元/千克)满足关系式y =ax -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.(1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大.解:(1)因为x =5时,y =11, 所以a2+10=11,a =2.(2)由(1)可知,该商品每日的销售量y =2x -3+10(x -6)2,所以商场每日销售该商品所获得的利润f (x )=(x -3)·⎣⎢⎡⎦⎥⎤2x -3+10(x -6)2=2+10(x -3)(x -6)2(3<x <6).从而,f ′(x )=10[(x -6)2+2(x -3)(x -6)] =30(x -4)(x -6).于是,当x 变化时,f ′(x ),f (x )的变化情况如表:由上表可得,x =4时,函数f (x )取得最大值,且最大值等于42.答:当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大. 专题六 定积分的应用由定积分求曲边梯形面积的方法步骤 (1)画出函数的图象,明确平面图形的形状. (2)通过解方程组,求出曲线交点的坐标. (3)确定积分区间与被积函数,转化为定积分计算.(4)对于复杂的平面图形,常常通过“割补法”求各部分的面积之和.【例8】如图所示,求由曲线y =x ,y =2-x ,y =-13x 所围成的图形的面积.解:由⎩⎨⎧y =x ,y =2-x ,⎩⎪⎨⎪⎧y =x ,y =-13x ,⎩⎪⎨⎪⎧y =2-x ,y =-13x ,得交点(1,1),(0,0),(3,-1),故S =1⎰⎣⎢⎡⎦⎥⎤x -⎝ ⎛⎭⎪⎫-13x d x +31⎰⎣⎢⎡⎦⎥⎤(2-x )-⎝ ⎛⎭⎪⎫-13x d x =1⎰⎝ ⎛⎭⎪⎫x +13x d x +31⎰⎝ ⎛⎭⎪⎫2-23x d x =3222136x x ⎛⎫+ ⎪⎝⎭10|+⎝ ⎛⎭⎪⎫2x -13x 231| =23+16+6-13×9-2+13=136. 专题七 恒成立问题 解决恒成立问题的方法(1)若关于x 的不等式f (x )≤m 在区间D 上恒成立,则转化为f (x )max ≤m . (2)若关于x 的不等式f (x )≥m 在区间D 上恒成立,则转化为f (x )min ≥m . (3)导数是解决函数f (x )的最大值或最小值问题的有力工具. 【例9】已知函数f (x )=x ln x .(1)若函数g (x )=f (x )+ax 在区间[e 2,+∞)上为增函数,求a 的取值范围; (2)若对任意x ∈(0,+∞),f (x )≥-x 2+mx -32恒成立,求实数m 的最大值.解:(1)由题意得g ′(x )=f ′(x )+a =ln x +a +1.∵函数g (x )在区间[e 2,+∞)上为增函数, ∴当x ∈[e 2,+∞)时,g ′(x )≥0, 即ln x +a +1≥0在[e 2,+∞)上恒成立. ∴a ≥-1-ln x .又当x ∈[e 2,+∞)时,ln x ∈[2,+∞). ∴-1-ln x ∈(-∞,-3],∴a ≥-3.(2)∵2f (x )≥-x 2+mx -3, 即mx ≤2x ·ln x +x 2+3. 又x >0,∴m ≤2x ·ln x +x 2+3x.令h (x )=2x ·ln x +x 2+3x,h ′(x )=(2x ln x +x 2+3)′·x -(2x ln x +x 2+3)·x ′x2=(2ln x +2+2x )x -(2x ln x +x 2+3)x2=2x +x 2-3x2, 令h ′(x )=0,解得x =1或x =-3(舍).当x ∈(0,1)时,h ′(x )<0,函数h (x )在[0,1)上单调递减,当x ∈(1,+∞)时,h ′(x )>0,函数h (x )在(1,+∞)上单调递增.∴h (x )min =h (1)=4, 即m 的最大值为4.。
高中数学第一章导数及其应用章末检测试卷新人教A版选修2-2(2021年整理)

2018-2019版高中数学第一章导数及其应用章末检测试卷新人教A版选修2-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019版高中数学第一章导数及其应用章末检测试卷新人教A版选修2-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019版高中数学第一章导数及其应用章末检测试卷新人教A版选修2-2的全部内容。
第一章导数及其应用章末检测试卷(一)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.由曲线y=x2,直线y=0和x=1所围成的图形的面积是()A。
错误!B。
错误!C。
错误!D。
错误!考点利用定积分求曲线所围成图形面积题点不需分割的图形的面积求解答案C解析由题意知,其围成的图形的面积为ʃ10x2d x=错误!错误!=错误!。
2.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内极小值点的个数为()A.1 B.2C.3 D.0考点函数极值的综合应用题点函数极值在函数图象上的应用答案A解析设极值点依次为x1,x2,x3且a<x1〈x2<x3〈b,则f(x)在(a,x1),(x2,x3)上单调递增,在(x1,x2),(x3,b)上单调递减,因此,x1,x3是极大值点,只有x2是极小值点.3.已知某物体运动的路程与时间的关系为s=错误!t3+ln t,则该物体在t=4时的速度为()A。
错误!B。
错误!C.错误!D。
错误!考点求瞬时速度题点用极限的思想求瞬时速度答案D解析s′(t)=t2+错误!,则该物体在t=4时的速度为s′|t=4=42+错误!=错误!。
2019秋新版高中数学人教A版选修2-2习题:第一章导数及其应用 1.5.3 Word版含解析.docx

1.5.3定积分的概念课时过关·能力提升基础巩固1设曲线f(x)在区间[a,b]上连续,将区间[a,b]n等分,在每个小区间上任取ξi,则f(x)d x等于()A.f(ξi)B.f(ξi)·-C.f(ξi)·ξiD.f(ξi)·(ξi-ξi-1)解析根据定积分的概念可知,B选项正确,其余均不等于f(x)d x,故选B.答案B2设连续函数f(x)>0,则当a<b时,定积分f(x)d x的符号()A.一定是正的B.一定是负的C.当0<a<b时是正的,当a<b<0时是负的D.以上结论都不正确解析根据定积分f(x)d x的几何意义可知,f(x)d x一定是正实数,故选A.答案A3下列各式中成立的是()A.[f(x)+5]d x=f(x)d x+5B.|x-1|d x=(1-x)d x+(x-1)d xC.-f(x)d x=-f(x)d x+f(x)d x=2f(x)d xD.-|f(x)|d x=--f(x)d x解析由于|x-1|d x=|x-1|d x+|x-1|d x=(1-x)d x+(x-1)d x,故B项正确.答案B4已知定积分f(x)d x=8,且f(x)为偶函数,则-f(x)d x等于()A.0B.16C.12D.8解析偶函数的图象关于y轴对称,故f(x)d x=2f(x)d x=16.故选B.-答案B5由函数y=-x的图象,直线x=1,x=0,y=0所围成的图形的面积可表示为()A.(-x)d xB.|-x|d xC.x d x D.-2x d x-解析由定积分的几何意义可知所求图形的面积为S=|-x|d x.答案B6不用计算,根据图形,比较下列各式的大小:(1)x d x x2d x(如图所示);(2)-d x2d x(如图所示).答案(1)>(2)<7(x-1)d x=.答案08把由y=cos x,x=0,x=,y=0所围成的图形的面积表示为定积分的形式是.解析由定积分的定义和几何意义求解.答案cos x d x能力提升1根据定积分的定义,x3d x不等于()-A.B.C.D.解析将[0,2]等分为n 个小区间 - (i=1,2,…,n ),若取ξi = - ,则 x 3d x= -,若取ξi =,则x 3d x=;将[0,2]等分成2n 个小区间 - (i=1,2,…,2n ),则Δx= ,取ξi =,则 x 3d x=.故选B.答案B2已知[f (x )+g (x )]d x=12,g (x )d x=6,则3f (x )d x 等于()A.12B.6C.18D.24解析∵ [f (x )+g (x )]d x=f (x )d x+g (x )d x ,∴ f (x )d x=12-6=6.∴3f (x )d x=3f (x )d x=3×6=18.答案C3设a=d x ,b= x 2d x ,c=x 3d x ,则a ,b ,c 的大小关系是( ) A.c>a>b B.a>b>c C.a=b>cD.a>c>b解析根据定积分的几何意义,易知x 3d x<x 2d x<d x ,即a>b>c ,故选B.答案B★4已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为v 甲和v乙(如图所示),那么对于图中给定的t 0和t 1,下列判断一定正确的是( )A.在t 1时刻,甲车在乙车前面B.t 1时刻后,甲车在乙车后面C.在t 0时刻,两车的位置相同D.t 0时刻后,乙车在甲车前面解析由题图可知,曲线v 甲比v 乙在0~t 0,0~t 1与t 轴所围成图形的面积大,则在t 0,t 1时刻,甲车均在乙车前面,故选A. 答案A5已知x2d x=x2d x=,则(x2+1)d x=.解析由定积分的性质,可得(x2+1)d x=x2d x+1d x,而由已知,有x2d x=x2d x+x2d x=.又由定积分的几何意义知1d x=1×2=2,故(x2+1)d x=+2=.答案6(1)计算---1)d x的值;(2)已知f(x)=∈-∈-∈求f(x)在区间[0,5]上的定积分.分析可先根据定积分的几何意义求出相关函数的定积分,再根据定积分的性质进行加减运算.解(1)如图,由定积分的几何意义,得--d x=-1d x=6.由定积分的性质,得---1)d x=--d x--1d x=-6.(2)如图,由定积分的几何意义,得x d x=×2×2=2,(4-x)d x=×(1+2)×1=,-d x=×2×1=1,所以f(x)d x=x d x+(4-x)d x+-d x=2++1=.★7弹簧在拉伸过程中,力与伸长量成正比,即力F(x)=kx(k为常数,x是伸长量),求弹簧从平衡位置拉长b所做的功.解将物体用常力F沿着力的方向移动距离x,则所做的功为W=Fx,本题F是克服弹簧拉力的变力,是移动距离x的函数F(x)=kx.将区间[0,b]n等分,记Δx=,分点依次为x0=0,x1=,x2=,…,x n-1=-,x n=b.当n很大时,在分段[x i,x i+1]所用的力约为kx i,所做的功ΔW i≈kx i·Δx=kx i·.则从0到b所做的总功W近似地等于-ΔW i=-kx i·Δx=-k·=[0+1+2+…+(n-1)]=--.于是得到弹簧从平衡位置拉长b所做的功为W=-ΔW i=-kb2.。
(新人教版)【文库精品】版高中数学 第一章 导数及其应用滚动训练二 新人教A版选修2-2【必做资料】
第一章导数及其应用滚动训练二(§1.3~§1.4)一、选择题1.函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( )A.无极大值点,有四个极小值点B.有三个极大值点,两个极小值点C.有两个极大值点,两个极小值点D.有四个极大值点,无极小值点考点函数极值的应用题点函数极值在函数图象上的应用答案 C解析f′(x)的符号由正变负,则f(x0)是极大值,f′(x)的符号由负变正,则f(x0)是极小值,由题图易知有两个极大值点,两个极小值点.2.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是( ) A.[1,+∞) B.a=1C.(-∞,1] D.(0,1)考点利用导数求函数的单调区间题点已知函数单调性求参数(或其范围)答案 A解析∵f′(x)=3x2-2ax-1,又f(x)在(0,1)内单调递减,∴不等式3x2-2ax-1≤0在(0,1)内恒成立,∴f′(0)≤0,且f′(1)≤0,∴a≥1.3.已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )A.f(b)>f(c)>f(d)B.f(b)>f(a)>f(e)C.f(c)>f(b)>f(a)D.f(c)>f(e)>f(d)考点 利用导数研究函数的单调性 题点 比较函数值的大小 答案 C解析 依题意得,当x ∈(-∞,c )时,f ′(x )>0, 因此,函数f (x )在(-∞,c )上是增函数, 由于a <b <c ,所以f (c )>f (b )>f (a ).4.函数f (x )=x +2cos x 在⎣⎢⎡⎦⎥⎤0,π2上取最大值时的x 值为( )A .0 B.π6 C.π3D.π2考点 利用导数求函数的最值 题点 利用导数求不含参数函数的最值 答案 B解析 由f ′(x )=1-2sin x =0,得sin x =12,又x ∈⎣⎢⎡⎦⎥⎤0,π2,所以x =π6,当x ∈⎣⎢⎡⎦⎥⎤0,π6时,f ′(x )>0;当x ∈⎣⎢⎡⎦⎥⎤π6,π2时,f ′(x )<0, 故当x =π6时取得最大值.5.已知函数f (x )=x 2(ax +b )(a ,b ∈R )在x =2处有极值,其图象在点(1,f (1))处的切线与直线3x +y =0平行,则函数f (x )的单调递减区间为( ) A .(-∞,0) B .(0,2) C .(2,+∞)D .(-∞,+∞)考点 利用导数求函数的单调区间 题点 利用导数求含参数函数的单调区间 答案 B解析 ∵f (x )=ax 3+bx 2,∴f ′(x )=3ax 2+2bx ,∴⎩⎪⎨⎪⎧3a ×22+2b ×2=0,3a +2b =-3,即⎩⎪⎨⎪⎧a =1,b =-3,令f ′(x )=3x 2-6x <0,则0<x <2.6.已知f (x )=x +b x在(1,e)上为单调函数,则实数b 的取值范围是( ) A .(-∞,1]∪[e 2,+∞) B .(-∞,0]∪[e 2,+∞) C .(-∞,e 2]D .[1,e 2]考点 利用导数求函数的单调区间 题点 已知函数的单调性求参数(或其范围) 答案 A解析 若b ≤0,则函数在(0,+∞)上为增函数,满足条件,若b >0,则函数的导数f ′(x )=1-b x 2=x 2-bx2,由f ′(x )>0得x >b 或x <-b ,此时函数单调递增, 由f ′(x )<0得-b <x <b ,此时函数单调递减, 若函数f (x )在(1,e)上为单调递增函数, 则b ≤1,即0<b ≤1,若函数f (x )在(1,e)上为单调递减函数, 则b ≥e,即b ≥e 2, 综上b ≤1或b ≥e 2,故选A.7.已知函数f (x )的图象是下列四个图象之一,且其导函数f ′(x )的图象如图所示,则该函数的图象是( )考点 函数的单调性与导数的关系 题点 根据导函数的图象确定原函数图象 答案 B解析 从导函数的图象可以看出,导函数值先增大后减小,x =0时最大,所以函数f (x )的图象的变化率也先增大后减小,在x =0时变化率最大.A 项,在x =0时变化率最小,故错误;C 项,变化率是越来越大的,故错误;D 项,变化率是越来越小的,故错误.B 项正确. 8.当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( ) A .[-5,-3] B.⎣⎢⎡⎦⎥⎤-6,-98 C .[-6,-2]D .[-4,-3]考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 答案 C解析 当x =0时,ax 3-x 2+4x +3≥0变为3≥0恒成立,即a ∈R .当x ∈(0,1]时,ax 3≥x 2-4x -3,a ≥x 2-4x -3x 3,∴a ≥⎣⎢⎡⎦⎥⎤x 2-4x -3x 3max .设φ(x )=x 2-4x -3x 3,φ′(x )=(2x -4)x 3-(x 2-4x -3)3x2x6=-x 2-8x -9x 4=-(x -9)(x +1)x 4>0, ∴φ(x )在(0,1]上递增,φ(x )max =φ(1)=-6, ∴a ≥-6.当x ∈[-2,0)时,a ≤x 2-4x -3x 3,∴a ≤⎣⎢⎡⎦⎥⎤x 2-4x -3x 3min . 仍设φ(x )=x 2-4x -3x 3,φ′(x )=-(x -9)(x +1)x 4. 当x ∈[-2,-1)时,φ′(x )<0, 当x ∈(-1,0)时,φ′(x )>0.∴当x =-1时,φ(x )有极小值,即为最小值. 而φ(x )min =φ(-1)=1+4-3-1=-2,∴a ≤-2.综上知-6≤a ≤-2. 二、填空题9.若函数f (x )=x 3+32x 2+m 在区间[-2,1]上的最大值为92,则m =________.考点 导数在最值问题中的应用题点 已知最值求参数 答案 2解析 f ′(x )=3x 2+3x =3x (x +1). 由f ′(x )=0,得x =0或x =-1. 又f (0)=m ,f (-1)=m +12,f (1)=m +52,f (-2)=-8+6+m =m -2,∴当x ∈[-2,1]时,最大值为f (1)=m +52,∴m +52=92,∴m =2.10.已知函数f (x )的导函数f ′(x )是二次函数,如图是f ′(x )的大致图象,若f (x )的极大值与极小值的和等于23,则f (0)的值为________.考点 利用导数研究函数的极值 题点 已知极值求参数 答案 13解析 ∵其导函数的函数值应在(-∞,-2)上为正数,在(-2,2)上为负数,在(2,+∞)上为正数,由导函数图象可知,函数在(-∞,-2)上为增函数,在(-2,2)上为减函数,在(2,+∞)上为增函数,∴函数在x =-2时取得极大值,在x =2时取得极小值,且这两个极值点关于点(0,f (0))对称,由f (x )的极大值与极小值之和为23,得f (-2)+f (2)=2f (0),∴23=2f (0),则f (0)的值为13. 11.已知函数f (x )=x e x+c 有两个零点,则c 的取值范围是________. 考点 函数极值的综合应用题点 函数零点与方程的根 答案 ⎝ ⎛⎭⎪⎫-∞,1e解析 ∵f ′(x )=e x(x +1),∴易知f (x )在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,且f (x )min =f (-1)=c -e -1,由题意得c -e -1<0,得c <e -1. 三、解答题12.某品牌电视生产厂家有A ,B 两种型号的电视机参加了家电下乡活动,若厂家对A ,B 两种型号的电视机的投放金额分别为p ,q 万元,农民购买电视机获得的补贴分别为110p ,25ln q 万元,已知A ,B 两种型号的电视机的投放总额为10万元,且A ,B 两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值.(精确到0.1,参考数据:ln 4≈1.4) 考点 利用导数求解生活中的最值问题 题点 利用导数求解最大利润问题解 设B 型号电视机的投放金额为x 万元(1≤x ≤9),农民得到的补贴为y 万元,则A 型号的电视机的投放金额为(10-x )万元,由题意得y =110(10-x )+25ln x =25ln x -110x +1,1≤x ≤9,∴y ′=25x -110,令y ′=0得x =4.由y ′>0,得1≤x <4,由y ′<0,得4<x ≤9, 故y 在[1,4)上单调递增,在(4,9]上单调递减,∴当x =4时,y 取得最大值,且y max =25ln 4-110×4+1≈1.2,这时,10-x =6.即厂家对A ,B 两种型号的电视机的投放金额分别为6万元和4万元时,农民得到的补贴最多,最多补贴约1.2万元.13.设函数f (x )=tx 2+2t 2x +t -1(x ∈R ,t >0). (1)求f (x )的最小值h (t );(2)若h (t )<-2t +m 对t ∈(0,2)恒成立,求实数m 的取值范围. 考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 解 (1)∵f (x )=t (x +t )2-t 3+t -1(x ∈R ,t >0), ∴当x =-t 时,f (x )有最小值f (-t )=h (t )=-t 3+t -1. (2)令g (t )=h (t )-(-2t +m )=-t 3+3t -1-m , 由g ′(t )=-3t 2+3=0得t =1或t =-1(舍去).当t 变化时,g ′(t ),g (t )的变化情况如下表:∴当t ∈(0,2)时,g (t )max =g (1)=1-m . ∵h (t )<-2t +m 对t ∈(0,2)恒成立, ∴g (t )max =1-m <0,∴m >1. 故实数m 的取值范围是(1,+∞). 四、探究与拓展14.已知函数f (x )=2ln x +a x2(a >0).若当x ∈(0,+∞)时,f (x )≥2恒成立,则实数a 的取值范围是________.考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 答案 [e ,+∞)解析 f (x )≥2即a ≥2x 2-2x 2ln x . 令g (x )=2x 2-2x 2ln x , 则g ′(x )=2x (1-2ln x ). 由g ′(x )=0得x =12e 或0(舍去), 当0<x <12e 时,g ′(x )>0; 当x >12e 时,g ′(x )<0,∴当x =12e 时,g (x )取最大值g (12e )=e ,∴a ≥e. 15.已知函数f (x )=ln(x +1)+axx +1(a ∈R ). (1)当a =1时,求函数f (x )在点(0,f (0))处的切线方程; (2)讨论函数f (x )的极值;(3)求证:ln(n +1)>1-112+2-122+3-132+…+n -1n 2(n ∈N *).考点 利用导数研究函数的单调性 题点 构造法的应用(1)解 当a =1时,f (x )=ln(x +1)+xx +1,所以f ′(x )=1x +1+(x +1)-x (x +1)2=x +2(x +1)2, 所以f ′(0)=2, 又f (0)=0,所以函数f (x )在点(0,f (0))处的切线方程为y =2x . (2)解 f ′(x )=1x +1+a (x +1)-ax(x +1)2=x +1+a(x +1)2(x >-1). 令x +1+a =0,得x =-a -1. 若-a -1≤-1,即a ≥0,则f ′(x )>0恒成立,此时f (x )无极值. 若-a -1>-1,即a <0, 当-1<x <-a -1时,f ′(x )<0, 当x >-a -1时,f ′(x )>0,此时f (x )在x =-a -1处取得极小值, 极小值为ln(-a )+a +1.(3)证明 当a =-1时,由(2)知,f (x )min =f (0)=0, 所以ln(x +1)-x x +1≥0,即ln(x +1)≥xx +1. 令x =1n(n ∈N *),则ln ⎝ ⎛⎭⎪⎫1n +1≥1n 1n+1=11+n ,所以lnn +1n ≥11+n. 又因为11+n -n -1n 2=1n 2(n +1)>0,所以11+n >n -1n 2,所以lnn +1n >n -1n2, 所以ln 21+ln 32+ln 43+…+ln n +1n >1-112+2-122+3-132+…+n -1n 2,即ln(n +1)>1-112+2-122+3-132+…+n -1n2.。
高中数学第一章导数及其应用1_3导数在研究函数中的应用教材习题点拨新人教A版选修22
(3) 因为 f ( x) =3x- x3,所以 f ′(x) = 3- 3x2.
当 f ′(x) > 0,即- 1< x< 1 时,函数 f ( x) =3x- x3 单调递增;
当 f ′(x) < 0,即 x> 1 或 x<- 1 时,函数 f ( x) = 3x- x3 单调递减.
(4) 因为 f ( x) =x3-x2- x,所以 f ′(x) = 3x2- 2x- 1.
当 x 变化时, f ′(x), f ( x) 变化情况如下表:
x
( -∞,- 2) - 2
( - 2,2)
2
(2 ,+∞)
f ′(x)
+
0
-
0
+
f ( x)
单调递增
16
单调递减
-16
单调递增
因此,当 x=- 2 时, f ( x) 有极大值,并且极大值为 16;
当 x=2 时, f ( x) 有极小值,并且极小值为- 16. (3) 因为 f ( x) =6- 12x+x3,所以 f ′(x) =- 12+ 3x2. 令 f ′(x) =- 12+ 3x2= 0,得 x= 2 或 x=- 2.
下面分两种情况讨论:
①当 f ′(x) > 0,即- 2<x< 2 时;
②当 f ′(x) < 0,即 x>2 或 x<- 2 时.
当 x 变化时, f ′(x), f ( x) 变化情况如下表:
x
( -∞,- 2)
-2
( - 2,2)
2
(2 ,+∞)
f ′(x -
)
0
+
0
-
f ( x)
单调递减
- 10 单调递增
当 x 变化时, f ′(x), f ( x) 变化情况如下表:
(全国通用版)2018_2019版高中数学第一章导数及其应用习题课导数的应用课件新人教A版选修2_2
解析
答案
反思与感悟 范围.
构造恰当函数并判断其单调性,利用单调性得到x的取值
跟踪训练 2
已知定义在 R 上的函数 f(x)满足 f(1)=1,且对任意的 x∈R
lg x+2 1 (0,10) 都有 f′(x)<3,则不等式 f(lg x)> 3 的解集为________.
解析
答案
类型二
利用导数研究函数的单调性
题型探究
类型一 命题角度1 比较函数值的大小
例1
π 已知定义在0,2上的函数
构造法的应用
f(x),f′(x)是它的导函数,且 sin x·
f′(x)>cos x· f(x)恒成立,则
A. 2f
π >f 6
π 4
B. 3f
π >f 6
1 1 1 1 fx - 2 ln ln f′(x)+ x <0,若 a=2 f , b =- 2 f , c = f ,则 a,b, 2 2 2
c 的大小关系是
A.a<c<b C.a<b<c
e 是自然对数的底数,a∈R. (1)当 a=1 时,求函数 f(x)的单调区间和极值;
解答
1 (2)求证:在(1)的条件下,f(x)>g(x)+ ; 2 1 ln x 1 证明 令 h(x)=g(x)+2= x +2,
1-ln x h′(x)= x2 ,x∈(0,e],
当0<x<e时,h′(x)>0,此时h(x)单调递增,
假设函数f(x)在[1,3]上不存在单调递增区间,
必有g(x)≤0,
(优选)2019年高中数学第一章导数及其应用1.6微积分基本定理优化练习新人教A版选修2-2
1.6 微积分基本定理[课时作业] [A 组 基础巩固]1.⎠⎛241xd x 等于( )A .-2ln 2B .2ln 2C .-ln 2D .ln 2解析:∵(ln x )′=1x,∴⎠⎛241xd x =(ln x )| 42=ln 4-ln 2=ln 2.答案:D2.如图,阴影区域的边界是直线y =0,x =2,x =0及曲线y =3x 2,则这个区域的面积是( )A .4B .8 C.13D.12解析:由定积分的几何意义,得S =⎠⎛023x 2dx =x 3| 20=23-0=8,故答案为B.答案:B3.定积分⎠⎛01(2x +e x)d x 的值为( )A .e +2B .e +1C .eD .e -1解析:⎠⎛01(2x +e x)d x =(x 2+e x)| 10=(1+e)-(0+e 0)=e ,因此选C.答案:C4.已知f (x )=2-|x |,则⎠⎛-12f (x )d x 等于( )A .3B .4C.72D.92解析:f (x )=2-|x |=⎩⎪⎨⎪⎧2-x ,x ≥0,2+x ,x <0,∴⎠⎛-12f (x )d x =⎠⎛-10(2+x )d x +⎠⎛02(2-x )d x =⎝ ⎛⎭⎪⎫2x +x 22| 0-1+⎝ ⎛⎭⎪⎫2x -x 22| 20=32+2=72.答案:C5.函数F (x )=⎠⎛0x t (t -4)d t 在[-1,5]上( )A .有最大值0,无最小值B .有最大值0和最小值-323C .有最小值-323,无最大值D .既无最大值也无最小值解析:F (x )=⎠⎛0x (t 2-4t )d t =⎝ ⎛⎭⎪⎫13t 3-2t 2|x 0=13x 3-2x 2(-1≤x ≤5).F ′(x )=x 2-4x ,由F ′(x )=0得x =0或x =4,列表如下:∴极大值F (0)=0,极小值F (4)=-3.又F (-1)=-73,F (5)=-253,∴最大值为0,最小值为-323.答案:B6.(2015·高考湖南卷)⎠⎛02(x -1)d x =________.解析:⎠⎛02(x -1)d x =⎝ ⎛⎭⎪⎫12x 2-x |20=(2-2)-0=0.答案:07.若⎠⎛1a (2x +1x)d x =3+ln 2,则a =________.解析:⎠⎛1a (2x +1x)d x =(x 2+ln x )|a1=a 2+ln a -1=3+ln 2, ∴a =2. 答案:28.设f (x )=⎩⎪⎨⎪⎧x 2,x ∈[0,1]1x,x ∈,(e 为自然对数的底数),则⎠⎛0ef (x )d x 的值为________.解析:依题意得⎠⎛0e f (x ) d x =⎠⎛01x 2d x +⎠⎛1e 1xd x=13x 3|10+ln x |e1=43. 答案:439.计算下列定积分: (1)⎠⎛12(2x 2-1x)d x ;(2)30π⎰(sin x -sin 2x )d x .解析:(1)函数y =2x 2-1x 的一个原函数是y =23x 3-ln x .所以⎠⎛12(2x 2-1x )d x =(23x 3-ln x )| 21=163-ln 2-23=143-ln 2.(2)函数y =sin x -sin 2x 的一个原函数为y =-cos x +12cos 2x .所以30π⎰(sin x -sin 2x )d x =(-cos x +12cos 2x )30π=(-12-14)-(-1+12)=-14.10.已知f (x )为二次函数,且f (-1)=2,f ′(0)=0,⎠⎛01f x d x =-2. (1)求f (x )的解析式;(2)求f (x )在[-1,1]上的最大值与最小值. 解析:(1)设f (x )=ax 2+bx +c (a ≠0),则f ′(x )=2ax +b .由f (-1)=2,f ′(0)=0,得⎩⎪⎨⎪⎧a -b +c =2b =0,即⎩⎪⎨⎪⎧c =2-ab =0.∴f (x )=ax 2+(2-a ).又⎠⎛01f (x )d x =⎠⎛01[ax 2+(2-a )]d x=[13ax 3+ (2-a )x ]|10=2-23a =-2, ∴a =6,∴c =-4.从而f (x )=6x 2-4. (2)∵f (x )=6x 2-4,x ∈[-1,1], 所以当x =0时,f (x )min =-4; 当x =±1时,f (x )max =2.[B 组 能力提升]1.若f (x )=x 2+2⎠⎛01f (x )d x ,则⎠⎛01f (x )d x =( )A .-1B .-13C.13D .1解析:令m =⎠⎛01f (x )d x ,则f (x )=x 2+2⎠⎛01f (x )d x =x 2+2m ,所以m =⎠⎛01f (x )d x =⎠⎛01⎝⎛⎭⎫x 2+2⎠⎛01f x d x d x = ⎠⎛01(x 2+2m )d x =⎠⎛01(x 2)d x +2m =13+2m ,所以m =-13⇒⎠⎛01f (x )d x =-13.答案:B2. ⎠⎛-33(x 3cos x )d x =________.解析:∵y =x 3cos x 为奇函数,∴⎠⎛-33 (x 3cos x )d x =0.答案:03.函数f (x )=sin(ωx +φ)的导函数y =f ′(x )的部分图象如图所示,其中,P 为图象与y 轴的交点,A ,C 为图象与x 轴的两个交点,B 为图象的最低点.(1)若φ=π6,点P 的坐标为⎝⎛⎭⎪⎫0,332,则ω=________.(2)若在曲线段ABC 与x 轴所围成的区域内随机取一点,则该点在△ABC 内的概率为________.解析:(1)y =f ′(x )=ωcos(ωx +φ),当φ=π6,点P 的坐标为⎝ ⎛⎭⎪⎫0,332时,ωcos π6=332,所以ω=3.(2)由题图知AC =T 2=πω,S △ABC =12AC ·ω=π2,设A ,C 的横坐标分别为a ,b .设曲线段ABC 与x 轴所围成的区域的面积为S ,则S =⎪⎪⎪⎪⎠⎛abf x d x =|f (x )| ba |=|sin(ωb +φ)-sin(ωa +φ)|=2, 由几何概型知该点在△ABC 内的概率为P =S △ABC S =π4. 答案:(1)3 (2)π44.设f (x )=ax +b 且⎠⎛-11f 2(x )d x =1,求f (a )的取值范围.解析:∵⎠⎛-11f 2(x )d x=⎠⎛-11 (a 2x 2+2abx +b 2)d x=(13a 2x 3+abx 2+b 2x )| 1-1 =23a 2+2b 2,∴23a 2+2b 2=1,∴a 2=32-3b 2, 又∵f (a )=a 2+b =-3b 2+b +32=-3(b -16)2+1912,∴当b =16时,f (a )max =1912.∴f (a )≤1912.5.若f (x )是一次函数,且⎠⎛01f (x )d x =5,⎠⎛01xf x d x =176.求⎠⎛12f x x d x 的值.解析:∵f (x )是一次函数,∴设f (x )=ax +b (a ≠0),由⎠⎛01(ax +b )d x =5得(12ax 2+bx )|10=12a +b =5.① 由⎠⎛01xf (x )d x =176得⎠⎛01(ax 2+bx )d x =176,即(13ax 3+12bx 2)|10=176,∴13a +12b =176.② 解①②得a =4,b =3,∴f (x )=4x +3, 于是⎠⎛12f x x d x =⎠⎛124x +3x d x =⎠⎛12(4+3x )d x=(4x +3ln x )|21=8+3ln 2-4=4+3ln 2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章导数及其应用滚动训练二(§1.3~§1.4)一、选择题1.函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( )A.无极大值点,有四个极小值点B.有三个极大值点,两个极小值点C.有两个极大值点,两个极小值点D.有四个极大值点,无极小值点考点函数极值的应用题点函数极值在函数图象上的应用答案 C解析f′(x)的符号由正变负,则f(x0)是极大值,f′(x)的符号由负变正,则f(x0)是极小值,由题图易知有两个极大值点,两个极小值点.2.若函数f(x)=x3-ax2-x+6在(0,1)内单调递减,则实数a的取值范围是( ) A.[1,+∞) B.a=1C.(-∞,1] D.(0,1)考点利用导数求函数的单调区间题点已知函数单调性求参数(或其范围)答案 A解析∵f′(x)=3x2-2ax-1,又f(x)在(0,1)内单调递减,∴不等式3x2-2ax-1≤0在(0,1)内恒成立,∴f′(0)≤0,且f′(1)≤0,∴a≥1.3.已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )A.f(b)>f(c)>f(d)B.f(b)>f(a)>f(e)C.f(c)>f(b)>f(a)D.f(c)>f(e)>f(d)考点 利用导数研究函数的单调性 题点 比较函数值的大小 答案 C解析 依题意得,当x ∈(-∞,c )时,f ′(x )>0, 因此,函数f (x )在(-∞,c )上是增函数, 由于a <b <c ,所以f (c )>f (b )>f (a ).4.函数f (x )=x +2cos x 在⎣⎢⎡⎦⎥⎤0,π2上取最大值时的x 值为( )A .0 B.π6 C.π3D.π2考点 利用导数求函数的最值 题点 利用导数求不含参数函数的最值 答案 B解析 由f ′(x )=1-2sin x =0,得sin x =12,又x ∈⎣⎢⎡⎦⎥⎤0,π2,所以x =π6,当x ∈⎣⎢⎡⎦⎥⎤0,π6时,f ′(x )>0;当x ∈⎣⎢⎡⎦⎥⎤π6,π2时,f ′(x )<0, 故当x =π6时取得最大值.5.已知函数f (x )=x 2(ax +b )(a ,b ∈R )在x =2处有极值,其图象在点(1,f (1))处的切线与直线3x +y =0平行,则函数f (x )的单调递减区间为( ) A .(-∞,0) B .(0,2) C .(2,+∞)D .(-∞,+∞)考点 利用导数求函数的单调区间 题点 利用导数求含参数函数的单调区间 答案 B解析 ∵f (x )=ax 3+bx 2,∴f ′(x )=3ax 2+2bx ,∴⎩⎪⎨⎪⎧3a ×22+2b ×2=0,3a +2b =-3,即⎩⎪⎨⎪⎧a =1,b =-3,令f ′(x )=3x 2-6x <0,则0<x <2.6.已知f (x )=x +b x在(1,e)上为单调函数,则实数b 的取值范围是( ) A .(-∞,1]∪[e 2,+∞) B .(-∞,0]∪[e 2,+∞) C .(-∞,e 2]D .[1,e 2]考点 利用导数求函数的单调区间 题点 已知函数的单调性求参数(或其范围) 答案 A解析 若b ≤0,则函数在(0,+∞)上为增函数,满足条件,若b >0,则函数的导数f ′(x )=1-b x 2=x 2-bx2,由f ′(x )>0得x >b 或x <-b ,此时函数单调递增, 由f ′(x )<0得-b <x <b ,此时函数单调递减, 若函数f (x )在(1,e)上为单调递增函数, 则b ≤1,即0<b ≤1,若函数f (x )在(1,e)上为单调递减函数, 则b ≥e,即b ≥e 2, 综上b ≤1或b ≥e 2,故选A.7.已知函数f (x )的图象是下列四个图象之一,且其导函数f ′(x )的图象如图所示,则该函数的图象是( )考点 函数的单调性与导数的关系 题点 根据导函数的图象确定原函数图象 答案 B解析 从导函数的图象可以看出,导函数值先增大后减小,x =0时最大,所以函数f (x )的图象的变化率也先增大后减小,在x =0时变化率最大.A 项,在x =0时变化率最小,故错误;C 项,变化率是越来越大的,故错误;D 项,变化率是越来越小的,故错误.B 项正确. 8.当x ∈[-2,1]时,不等式ax 3-x 2+4x +3≥0恒成立,则实数a 的取值范围是( ) A .[-5,-3] B.⎣⎢⎡⎦⎥⎤-6,-98 C .[-6,-2]D .[-4,-3]考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 答案 C解析 当x =0时,ax 3-x 2+4x +3≥0变为3≥0恒成立,即a ∈R .当x ∈(0,1]时,ax 3≥x 2-4x -3,a ≥x 2-4x -3x 3,∴a ≥⎣⎢⎡⎦⎥⎤x 2-4x -3x 3max .设φ(x )=x 2-4x -3x 3,φ′(x )=(2x -4)x 3-(x 2-4x -3)3x2x6=-x 2-8x -9x 4=-(x -9)(x +1)x 4>0, ∴φ(x )在(0,1]上递增,φ(x )max =φ(1)=-6, ∴a ≥-6.当x ∈[-2,0)时,a ≤x 2-4x -3x 3,∴a ≤⎣⎢⎡⎦⎥⎤x 2-4x -3x 3min . 仍设φ(x )=x 2-4x -3x 3,φ′(x )=-(x -9)(x +1)x 4. 当x ∈[-2,-1)时,φ′(x )<0, 当x ∈(-1,0)时,φ′(x )>0.∴当x =-1时,φ(x )有极小值,即为最小值. 而φ(x )min =φ(-1)=1+4-3-1=-2,∴a ≤-2.综上知-6≤a ≤-2. 二、填空题9.若函数f (x )=x 3+32x 2+m 在区间[-2,1]上的最大值为92,则m =________.考点 导数在最值问题中的应用题点 已知最值求参数 答案 2解析 f ′(x )=3x 2+3x =3x (x +1). 由f ′(x )=0,得x =0或x =-1. 又f (0)=m ,f (-1)=m +12,f (1)=m +52,f (-2)=-8+6+m =m -2,∴当x ∈[-2,1]时,最大值为f (1)=m +52,∴m +52=92,∴m =2.10.已知函数f (x )的导函数f ′(x )是二次函数,如图是f ′(x )的大致图象,若f (x )的极大值与极小值的和等于23,则f (0)的值为________.考点 利用导数研究函数的极值 题点 已知极值求参数 答案 13解析 ∵其导函数的函数值应在(-∞,-2)上为正数,在(-2,2)上为负数,在(2,+∞)上为正数,由导函数图象可知,函数在(-∞,-2)上为增函数,在(-2,2)上为减函数,在(2,+∞)上为增函数,∴函数在x =-2时取得极大值,在x =2时取得极小值,且这两个极值点关于点(0,f (0))对称,由f (x )的极大值与极小值之和为23,得f (-2)+f (2)=2f (0),∴23=2f (0),则f (0)的值为13. 11.已知函数f (x )=x e x+c 有两个零点,则c 的取值范围是________. 考点 函数极值的综合应用题点 函数零点与方程的根 答案 ⎝ ⎛⎭⎪⎫-∞,1e解析 ∵f ′(x )=e x(x +1),∴易知f (x )在(-∞,-1)上单调递减,在(-1,+∞)上单调递增,且f (x )min =f (-1)=c -e -1,由题意得c -e -1<0,得c <e -1. 三、解答题12.某品牌电视生产厂家有A ,B 两种型号的电视机参加了家电下乡活动,若厂家对A ,B 两种型号的电视机的投放金额分别为p ,q 万元,农民购买电视机获得的补贴分别为110p ,25ln q 万元,已知A ,B 两种型号的电视机的投放总额为10万元,且A ,B 两种型号的电视机的投放金额均不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出最大值.(精确到0.1,参考数据:ln 4≈1.4) 考点 利用导数求解生活中的最值问题 题点 利用导数求解最大利润问题解 设B 型号电视机的投放金额为x 万元(1≤x ≤9),农民得到的补贴为y 万元,则A 型号的电视机的投放金额为(10-x )万元,由题意得y =110(10-x )+25ln x =25ln x -110x +1,1≤x ≤9,∴y ′=25x -110,令y ′=0得x =4.由y ′>0,得1≤x <4,由y ′<0,得4<x ≤9, 故y 在[1,4)上单调递增,在(4,9]上单调递减,∴当x =4时,y 取得最大值,且y max =25ln 4-110×4+1≈1.2,这时,10-x =6.即厂家对A ,B 两种型号的电视机的投放金额分别为6万元和4万元时,农民得到的补贴最多,最多补贴约1.2万元.13.设函数f (x )=tx 2+2t 2x +t -1(x ∈R ,t >0). (1)求f (x )的最小值h (t );(2)若h (t )<-2t +m 对t ∈(0,2)恒成立,求实数m 的取值范围. 考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 解 (1)∵f (x )=t (x +t )2-t 3+t -1(x ∈R ,t >0), ∴当x =-t 时,f (x )有最小值f (-t )=h (t )=-t 3+t -1. (2)令g (t )=h (t )-(-2t +m )=-t 3+3t -1-m , 由g ′(t )=-3t 2+3=0得t =1或t =-1(舍去).当t 变化时,g ′(t ),g (t )的变化情况如下表:∴当t ∈(0,2)时,g (t )max =g (1)=1-m . ∵h (t )<-2t +m 对t ∈(0,2)恒成立, ∴g (t )max =1-m <0,∴m >1. 故实数m 的取值范围是(1,+∞). 四、探究与拓展14.已知函数f (x )=2ln x +a x2(a >0).若当x ∈(0,+∞)时,f (x )≥2恒成立,则实数a 的取值范围是________.考点 利用导数求函数中参数的取值范围 题点 利用导数求恒成立问题中参数的取值范围 答案 [e ,+∞)解析 f (x )≥2即a ≥2x 2-2x 2ln x . 令g (x )=2x 2-2x 2ln x , 则g ′(x )=2x (1-2ln x ). 由g ′(x )=0得x =12e 或0(舍去), 当0<x <12e 时,g ′(x )>0; 当x >12e 时,g ′(x )<0,∴当x =12e 时,g (x )取最大值g (12e )=e ,∴a ≥e. 15.已知函数f (x )=ln(x +1)+axx +1(a ∈R ). (1)当a =1时,求函数f (x )在点(0,f (0))处的切线方程; (2)讨论函数f (x )的极值;(3)求证:ln(n +1)>1-112+2-122+3-132+…+n -1n 2(n ∈N *).考点 利用导数研究函数的单调性 题点 构造法的应用(1)解 当a =1时,f (x )=ln(x +1)+xx +1,精品学习资料所以f ′(x )=1x +1+(x +1)-x (x +1)2=x +2(x +1)2, 所以f ′(0)=2, 又f (0)=0,所以函数f (x )在点(0,f (0))处的切线方程为y =2x . (2)解 f ′(x )=1x +1+a (x +1)-ax(x +1)2=x +1+a(x +1)2(x >-1). 令x +1+a =0,得x =-a -1. 若-a -1≤-1,即a ≥0,则f ′(x )>0恒成立,此时f (x )无极值. 若-a -1>-1,即a <0, 当-1<x <-a -1时,f ′(x )<0, 当x >-a -1时,f ′(x )>0,此时f (x )在x =-a -1处取得极小值, 极小值为ln(-a )+a +1.(3)证明 当a =-1时,由(2)知,f (x )min =f (0)=0, 所以ln(x +1)-x x +1≥0,即ln(x +1)≥xx +1. 令x =1n(n ∈N *),则ln ⎝ ⎛⎭⎪⎫1n +1≥1n 1n+1=11+n ,所以lnn +1n ≥11+n. 又因为11+n -n -1n 2=1n 2(n +1)>0,所以11+n >n -1n 2,所以lnn +1n >n -1n2, 所以ln 21+ln 32+ln 43+…+ln n +1n >1-112+2-122+3-132+…+n -1n 2,即ln(n +1)>1-112+2-122+3-132+…+n -1n2.精品学习资料。
