点阵材料抛物面结构的参数化有限元建模方法及赋形分析
轻质点阵结构的参数化建模及力学性能研究分析论文

轻质点阵结构的参数化建模及力学性能研究分析论文轻质点阵结构的参数化建模及力学性能研究分析论文引言随着3D打印技术和材料制备技术的高速发展,轻质多孔点阵材料作为近年来兴起的力学性能极为优异的新一代轻质高强多功能材料,广泛应用于组织工程学、航空航天、船舶制造等领域。
相比传统材料,轻质多孔点阵材料最大不同在于其具有千变万化的微结构和高孔隙率(大于7000),因面具有轻质量、高强度、高效散热、能吸收电磁波,以及多功能可设计性等特有的优良性能。
近年来,相关轻质点阵结构力学性能的研究受到了国内外专家的高度重视。
Dede等介绍了一种设计单层或多层的周期性点阵结构技术,并对单层点阵结构进行了力学性能的计算分析。
张钱城等根据各类轻质点阵材料的胞元结构分析其力学性能,并分析了强化轻质点阵结构力学性能的主要方法。
陈立明等通过对轻质点阵夹层的力学性能研究,利用轻质点阵结构的均质化等效理论模型,建立了轻质点阵圆柱壳的强度模型以及刚度模型,最后与有限元分析结果进行了对比验证。
Tekoglu等通过对多孔点阵材料在压缩、弯曲和剪切条件下的理论和仿真分析,研究了其单元尺寸变化对力学性能的影响关系。
Fan等对轻质点阵结构力学性能提出了理论模型方法并对其进行了相应的试验研究。
以上研究多为对胞元形式构成的点阵结构模型的力学性能的研究,面没有涉及对胞元结构参数化建模以及多种胞元结构构建试件的对比研究。
本文设计了基于长方体空间微结构衍生的胞元结构,并建立其数学模型以构建试件的参数化模型及分析系统。
针对分别由边结构、顶点结构、面心结构、互连顶点结构以及内十字心结构构建的长方体试件,通过改变胞元尺寸及数量或胞元支柱截面半径,保证试件结构尺寸及质量不变,分析比较在拉压、弯曲、扭转情况下试件的力学性能,并通过动力学模态分析进行验证,提出了在各种载荷下点阵结构材料的设计方法。
1轻质点阵结构参数化建模1. 1胞元结构设计轻质多孔点阵材料通过模拟分子点阵构型,并由节点和节点间连接杆件单元组成一种具有周期性的拓扑结构,不同的胞元结构构成的点阵材料会产生千差万别的力学性能。
有限元模型建模过程

有限元模型建模过程有限元模型建模,这可真是个技术活儿,就像盖房子一样,每一块砖头都得放对地方,每一根钢筋都得恰到好处。
咱们先来说说模型的简化。
这一步就好比是给一个大胖子瘦身,把那些不重要的、对结果影响不大的细节给去掉。
你想想,要是不简化,模型复杂得就像一团乱麻,处理起来能把人给累趴下!比如说,一个机械零件上的小小倒角,在某些情况下,对整体的力学性能影响微乎其微,那就别让它来捣乱啦。
接下来是网格划分。
这网格就像是一张大网,把模型分割成一个个小格子。
网格划分得好不好,直接关系到计算结果的准确性和效率。
要是网格太粗糙,就像用大网眼去捞小鱼,很多关键信息都给漏掉了;要是网格太细密,那计算量可就大得吓人,等结果出来,花儿都谢了。
所以得根据实际情况,拿捏好这个度。
再说说材料属性的定义。
这就好比给每个零件穿上合适的衣服,不同的材料有不同的特性,强度、硬度、弹性模量等等。
如果把钢的属性给了塑料,那得出的结果不就闹笑话了吗?边界条件的设定也很关键。
这就像是给模型装上了轨道,规定它能怎么动,不能怎么动。
比如说,一个固定的支撑点,就得让它老老实实呆着,不能乱跑;一个施加的力,就得搞清楚方向和大小。
不然,模型就像脱缰的野马,不知道跑到哪里去了。
加载条件的确定也不能马虎。
这就像是给模型加上担子,担子有多重,放在哪里,都得心里有数。
加载不当,结果可能就差之千里。
模型检查也是必不可少的一步。
这就像考试前的检查试卷,看看有没有漏题,有没有写错。
检查网格质量、材料属性、边界条件等等,一个小错误都可能导致全盘皆输。
有限元模型建模可不简单,需要耐心和细心,就像雕琢一件艺术品。
每一个步骤都不能掉以轻心,每一个参数都得反复斟酌。
只有这样,才能得到准确可靠的结果,为我们的设计和分析提供有力的支持。
你说是不是?总之,有限元模型建模是个精细活,得用心对待,才能收获满意的成果!。
有限元建模方法分析

2.6 边界条件处理
基于位移法的有限元法,在结构边界上严格满足已知 的位移约束条件。
根据实际边界约束情况,对模型的某些节点施加约束,
消除结构刚体位移和局部可变机构的可能性 。
2.7 连接条件的处理
复杂结构常由杆、梁、板、壳、二维体、三维体等形式 的构件构成。由于各构件之间(梁和二维体、板壳和三维体) 的自由度个数不匹配。连接条件的处理方式:
准则:
①满足平衡条件——结构的整体和任一单元在节点上
都必须保持静力平衡。
②满足变形协调条件——交汇于一点上的各元素在外
力作用下,引起元素变形后必须仍保持交汇于一点。
准则:
③满足边界条件(包括整个结构边界条件及单元间的边界 条件)和材料的本构关系。
④刚度等价原则——有限元模型的抗弯、抗扭、抗拉及 抗剪刚度应尽可能等价。
单元——100多种单元类型。单元分为二维和三维, 具有点、线、面或体的形式,可选用线性和二次(带边中 节点)单元
二、有限元分析过程
§3-4 有限元建模方法
二、有限元分析过程
§3-4 有限元建模方法
有限元分析过程:3个阶段
1.建模阶段 2.计算阶段 3.后处理阶段
关键:建立有限元模型
1、有限元模型为计算提供所有原始数据,模型误差大, 可能产生与实际完全不符的分析结果
1.有限元离散模型的有效性确认
1.2 有限元模型的性能指标
有限元模型是借助于计算机进行分析的离散近似模 型。线性静力问题,包括有限元网格的离散点组成的近 似几何模型,由材料力学特性数据和单元刚度矩阵表达 的变形应力近似、外载荷近似和边界条件近似。
要控制和减小误差,有限元模型应满足性能指标:
1)可靠性
模缩小。
ANSYS参数化有限元技术在板壳结构拓扑优化设计中的应用

ANSYS参数化有限元技术在板壳结构拓扑优化设计中的应用王峰;丁晓红;陈建来
【期刊名称】《机械设计与制造》
【年(卷),期】2008(000)001
【摘要】拓扑优化设计是工程结构降低成本、提高性能的有效手段之一.在ANSYS对加筋板壳结构的有限元分析基础上,可以对板壳结构的加强部件分布进行合理设计.着重介绍了使用ANSYS参数化语言进行加筋板壳结构的分析方法.【总页数】3页(P27-29)
【作者】王峰;丁晓红;陈建来
【作者单位】上海理工大学,机械工程学院,上海,200093;上海理工大学,机械工程学院,上海,200093;上海理工大学,机械工程学院,上海,200093
【正文语种】中文
【中图分类】TH12;O224
【相关文献】
1.ANSYS参数化有限元技术在人行天桥结构分析中的应用 [J], 姚莉莉;徐虎;蔡贵春
2.基于ANSYS参数化语言的微结构拓扑优化设计 [J], 张军化;谢桂兰
3.离散变量板壳结构拓扑优化设计及其应用 [J], 柴山;曲庆文;李建新;王凤生
4.浅析ANSYS在桥梁拓扑优化设计中的应用 [J], 梅来彬;王波
5.ANSYS参数化设计语言及其在电除尘器荷载梁优化设计中的应用 [J], 王学文;杨兆建
因版权原因,仅展示原文概要,查看原文内容请购买。
第二讲有限元建模

➢ 实常数的计算(重点3)
➢ 常规截面(矩形,圆形,圆环),可以手算
➢ ANSYS提供的截面面积(工字型,槽钢等)
➢ 复杂结构(箱型梁):借助AUTOCAD和ANSYS
➢ 第一步:在CAD里画出我们的图形。 第二步:建立UCS,然后把UCS的中心确定在横向和纵向线的中心上,具体步骤如下:命令UCS→N→ 捕捉中心 第三步:建立块。步骤如下:命令 region ,然后选择特殊图形闭合区域面域化 命令 subtract 实现图形的加减。 第四步:质量属性查询。命令 MassProp。
第二讲有限元建模
第1页,本讲稿共19页
有限元法的建模的流程
➢ 建模流程
前处理(建模)
分析物理问题
加载 求解 后处理(分析)
确定结构组成 确定分析类型
单元类型 材料属性
实常数(几何特征) 确定建模方式 简化模型
(依据物理问题)
建模
第2页,本讲稿共19页
有限元建模基础
➢ 模型的定义
➢ 模型传统定义是把实物按比例缩小做成的 东西
孔径1 1
0.5 2
1
1
1
4
第18页,本讲稿共19页
实例2
.55 21
5
R0.5
R0.2
1
2 1 2.5 2.5 0.5 8.5
第19页,本讲稿共19页
面体进行划分,采用网格数量、边长及曲率来控制网格的质量。
第12页,本讲稿共19页
网格划分
➢ 网格质量的评估(难点)
➢ 单元的质量和数量对求解结果和求解过程影响较大,如果结构单元全部由等边三角形、正方形、正四 面体、立方六面体等单元构成,则求解精度可接近实际值,但由于这种理想情况在实际工程结构中很 难做到。因此根据模型的不同特征,设计不同形状种类的网格,有助于改善网格的质量和求解精度。 单元质量评价一般可采用以下几个指标:
有限元分析建模及若干问题PPT课件
a、线弹性支座:当支承结构或基础受外载产生较大的弹 性变形时,这种支座称为弹性支座。根据支反力的不同, 弹性支承可分为弹性线支座和弹性铰支座,它们分别产生 弹性线位移/支反力、线性角位移/反力矩。如图
b、非线性支座
c、斜支座
u
C)装配应力和温度应力 D)油缸/软绳问题(不可拉/压)
φ v
第17页/共37页
0.5
0.5
P
0.5
P
P
0.5
P
P
=
+
原结构
对称载荷
反对称载荷
第12页/共37页
9-6 模型简化
4)小特征删除 由于实际机械零件设计中很多结构的变化是因加工、装配、
调试等功能所需的并非或强度、刚度设计所重点关注的。 因而在对其进行力学分析计算时,可将这类细小的结构忽 略不计。如机械结构中常有的小孔、倒角、凸台、凹槽等。 这些结构通常尺寸较小,如不省略,反而会导致网格划分 困难,节点单元增加,如图所示为一经细节删除操作后有 限元网格模型。 几何模型简化操作实例
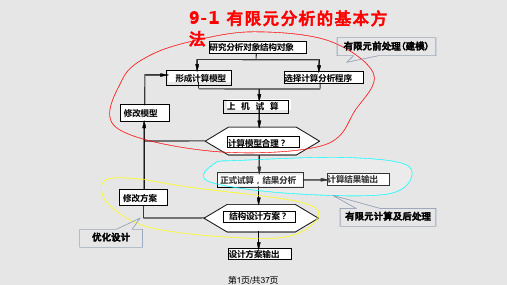
9-1 有限元分析的基本方
法 研究分析对象结构对象
有限元前处理(建模)
形成计算模型
选择计算分析程序
修改模型
上机试算
计算模型合理?
修改方案
优化设计
正式试算,结果分析 结构设计方案?
计算结果输出
有限元计算及后处理
设计方案输出 第1页/共37页
9-1 有限元分析的基本方法
1)建立实际工程问题的计算模型 利用几何、载荷的对称性简化模型, 建立等效模型
第15页/共37页
9-6 模型简化
• b、固定铰支:它与活动铰支的区别在于整个支座不能移 动,但是被支撑的结构可绕固定轴线或铰自由转动。如图。
有限元建模与分析技巧报告
我国的力学工作者为有限元方法的初期发展做出了许多 贡献,其中比较著名的有:陈伯屏(结构矩阵方法), 钱令希(余能原理),钱伟长(广义变分原理),胡 海昌(广义变分原理),冯康(有限单元法理论), 冯钟越(结构有限元分析)。
在1963年前后,经过(卞学磺)等许多人的工作,认识 到有限元法就是变分原理中Ritz近似法的一种变形,从 而发展了使用各种不同变分原理导出的有限元计算公 式。
有限元法的起源
1965年和(张佑启)发现,对于所有的场问题,只要能 将其转换为相应的变分形式,即可以用与固体力学有 限元法的相同步骤求解。
• 其中包括非线性结构分析ADINA。 温度场分析 ADINA-T 流体动力导分析 ADINA-F 流固耦合分析 ADINA FSI 后处理 ADINA PLOT 完整的交互界面 ADINA CAE
Nastran软件简介
由来 版本 文档
Nastran软件的由来
• Nastran,即NASA 结构分析系统,是1966年美国 国家航空航天局(NASA)为了满足当时航空航天工 业对结构分析的迫切需求,主持开发大型应用有
有限元建模与分析技巧报告
讲课题目
有限元建模与分析技巧
讲课提纲
一、有限元分析简介 二、工程分析软件 三、 Patran建模实例 四、交流、提问
有限元分析简介
起源 发展现状
有限元法的起源
有限元法的形成可以回顾到二十世纪50年代,来 源于固体力学中矩阵结构法的发展和工程师对 结构相似性的直觉判断。从固体力学的角度来 看,桁架结构等标准离散系统与人为地分割成 有限个分区后的连续系统在结构上存在相似性。
轻质点阵结构的参数化建模及力学性能研究
轻质点阵结构的参数化建模及力学性能研究
轻质点阵结构是一种特殊而具有创新性的结构形式,它具有结构轻巧、强度高、刚度大、形式多样等优点。
近年来,它的应用越来越广泛,成功的例子包括教室的天花板以及
医疗设备部件。
这种点阵结构能够满足越来越多的应用需求,但是由于它结构较复杂,所
以如何参数化建模和优化设计仍然是一个难题。
基于参数化建模,设计轻质点阵结构有助于缩减开发周期和提高质量,从而提高效率,减少成本。
为了建立轻质点阵结构,首先利用凸优化和可行性算法,以及计算机辅助工程(CAE)软件开发的参数化建模技术,结合有限元分析,从而实现参数化设计。
其次,轻
质点阵结构的力学性能要根据设计要求对模型进行优化,以达到最佳的力学性能。
进行参数化建模时,我们采用CAE软件,并采用有限元分析方法来完成数值分析,就
可以很快实现力学特性分析。
通过参数化建模,我们可以准确选择结构参数,从而获得优
化的最佳结构参数组合。
根据不同的物理属性,轻质点阵结构可以实现最佳的力学性能。
同时,利用软件管理技术可以实现模型加工,并验证模型是否符合实际要求,以确保最终
的设计质量。
通过上述的分析,参数化建模和优化设计是轻质点阵结构的一个重要研究方向,可用
于实现高效有效的设计与生产,进而实现高性能、高可靠性与低成本的设计要求。
自行火炮有限元参数化建模方法
自行火炮有限元参数化建模方法
楚志远;杨国来;陈运生
【期刊名称】《南京理工大学学报(自然科学版)》
【年(卷),期】2002(026)002
【摘要】该文通过对典型的CAD软件输出的有限元模型的分析,提出了自行火炮有限元参数化建模方法。
通过修改节点局部坐标系实施数据转换,指出了参数化建模的关键问题,编制了相应的转换程序,可方便地处理不同的射击工况,解决了自行火炮有限元法重复建模的问题。
结合某自行火炮进行了参数化建模,证明该方法技术途径可行,这对解决火炮工程问题具有重要的实用价值。
【总页数】4页(P120-122,156)
【作者】楚志远;杨国来;陈运生
【作者单位】南京理工大学机械工程学院,南京,210094;南京理工大学机械工程学院,南京,210094;南京理工大学机械工程学院,南京,210094
【正文语种】中文
【中图分类】TJ818,TP319.9
【相关文献】
1.型材拉弯成形过程的参数化有限元建模方法 [J], 张学广
2.基于Isight的冲压驱动桥壳参数化有限元建模方法 [J], 刘博林;谢里阳;张娜;罗义建
3.线膛身管有限元网格参数化建模方法 [J], 邹利波;于存贵;郭昭蔚;冯广斌
4.点阵材料抛物面结构的参数化有限元建模方法及赋形分析 [J], 赵航;张华振;兰澜;
伍科;姜恒坤
5.一种新的土石坝三维有限元参数化建模方法 [J], 黄明镇;金海
因版权原因,仅展示原文概要,查看原文内容请购买。
有限元建模方法
单元数量
真实解
二次单元
最
一次单元
大
变
形
单元数量
2、控制规模原则
1)计算时间 2)存储容量 3)计算精度 4)其 他
五、建模的一般步骤
软件 单元库
分几单单网模边
实际结构 设计方案
析 问 题 定
何 模 型 建
元 类 型 选
元 特 性 定
格 划
型 检
界 条
有限元模型
计算
件
定
义立择义分查义
2 2个移动自由度
空间轴对称结构
2
3个移动自由度 3个转动自由度
2
3个移动自由度 3个转动自由度
1
2个移动自由度 1个转动自由度
1
3个移动自由度 (平面杆单元2个)
平板结构 曲面壳体 轴对称曲面壳体 桁杆结构
1
3个移动自由度(平面梁2个) 3个转动自由度(平面梁1个)
梁结构
1
3个移动自由度(平面2个) 3个转动自由度(平面1个)
3、自适应分网(Adaptive meshing)
2.5 边界条件定义
一、位移约束条件 Displacement Restraints
1、位移约束的必要性
二、载荷条件
1、集中载荷
Concentrated Load
Nodal Load
2、分布载荷 Distributed Load
三、体积力 Volume Load
……
2.4 网格划分方法
一、网格划分原则 1、网格数量 (Number of mesh )
accuracy time
2、网格疏密 ( relative density)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点阵材料抛物面结构的参数化有限元建模方法及赋形分析赵航1,张华振1,2,兰澜2,伍科1,姜恒坤1(1援中国空间技术研究院西安分院,西安710000;2.上海跃盛信息技术有限公司,上海200240)摘要:针对点阵材料抛物面结构进行有限元分析时的几何建模需求,提出了一种点阵材料抛物面结构的参数化有限元建模方法。
首先,利用数学公式表征出抛物面结构在平面投影区域内的点阵材料胞元特征点坐标信息,生成点阵材料的平面几何模型。
然后,采用映射法将平面模型映射到标准抛物面,并将抛物面上每一胞元特征点进行有序编号,基于该特征点序号,编译循环程序,根据需求划分网格生成相应的节点和单元。
基于该方法,建立了手性六边形点阵材料抛物面结构的有限元模型,进行了初步的胞元几何参数优化,并通过分析该抛物面结构重构赋形时的变形能力和最大应力,初步验证文中方法的有效性,为手性六边形点阵材料抛物面结构的进一步优化分析奠定了基础。
关键词:参数化建模;手性六边形点阵材料;可重构赋形反射面;抛物面天线中图分类号:TP391.7文献标志码:A文章编号:员园园圆原圆猿猿猿(圆园员9)01原园153原园4 Parametric Finite Element Modeling Method and Shape Analysis of Lattice Material Parabolic Structure ZHAO Hang1,ZHANG Huazhen1,2,LAN Lan2,WU Ke2,JIANG Hengkun1(1.China Academy of Space Technology(Xi’an),Xi’an710000,China;2.Shanghai YS Information Technology Co.,Ltd.,Shanghai200240,China) Abstract:A parametric finite element modeling method for lattice material parabolic structure is proposed for geometric modeling of finite element analysis for lattice material parabolic structure.Firstly,the mathematical formula is used torepresent the coordinate information of the lattice material cell of the parabolic structure in the plane projection area,and the planar geometric model of the lattice material is generated.Then,the mapping method is used to map the planar model to the standard paraboloid,and each cell feature point on the paraboloid is numbered sequentially.Based on the feature point number,the loop program is compiled,and the corresponding nodes and units are generated according to the requirements.Based on the method,the finite element model of chiral hexagon lattice material parabolic structure is established,and the preliminary optimization of cell geometry parameters is carried out.By analyzing the parabolic structure and reconstructing the deformability and maximum stress during shaping,the method of the method is preliminarily verified.The effectiveness lays the foundation for further optimization analysis of the chiral hexagon lattice material parabolic structure.Keywords:parametric modeling;chiral hexagon lattice material;reconfigurable shaped reflective surface;parabolic antenna0引言近年来,随着卫星通信的发展和需求,在轨可重构赋形天线成为一个具有重要研究意义和实用价值的研究方向。
其中,对反射面进行机械式重构是一个可行性和经济性较高的选择[1-5]。
Leri等[6]应用一种柔性复合材料制成反射面结构并进行重构实验,该结构具有较高的重构赋形精度,但在施加载荷的局部区域易产生屈曲影响形面精度;宋思扬等[7]对碳纤维铝蜂窝夹层结构的平面反射器结构进行重构实验,但该实验仅研究了平面蜂窝结构的赋形能力。
目前对于机械重构赋形天线领域,找到一种合理、高效的反射面赋形材料是一个关键。
在航空领域,Micheal等[8]将一种全新的负泊松比点阵材料应用于可变形机翼研究,该材料具有变形能力强以及能够实现弹性变形的优点。
基于Micheal等学者研究工作的启发,本文将这种点阵材料引入星载天线机械赋形重构,通过有限元法对在一定工况下该材料的赋形能力和应力状况进行了分析。
在确定适用于作为可重构赋形反射面结构的点阵材料的早期设计阶段,为得到重构赋形工况下抛物面上的最大应力和赋形精度,需要按照点阵材料抛物面的实际几何结构构建它的有限元模型。
对于较为复杂的仿真分析,有限元建模占到整个分析工作量的70%[9],包括几何建模、网格划分、边界条件定义和材料参数定义四部分内容。
在建立点阵材料抛物面结构的有限元模型时,会遇到下述三个问题:1)由于点阵材料抛物面结构不能像平面点阵材料那样通过直接阵列的方式生成胞元,模型结构过于复杂,所以通过人工交互基于CAD模型的有限元建模工作量过大[10],时间成本过高且难以自动运行,不利于后续的胞元几何参数优化工作;2)由于点阵材料的胞元形式众多且几何重复而复杂,现有的文献多是对各种点阵材料胞元的平面结构进行建模分析[11],对于点阵材料的复杂曲面的建模分析很少;3)由于点阵材料的胞元结构较为复杂,包含不同长度的边,所以用有限元软件自动生成网格时,胞元各边上的网格大小比例无法控制,需要一种可自定义胞元各边上网格大小的网格生成方法。
针对点阵材料抛物面结构在重构赋形工况下的赋形和受力分析需求,为提高该点阵材料抛物面结构的设计质量和分析效率,本文拟采用参数化有限元建模方法建立其有限元模型。
本文研究了手性六边形负泊松比点阵材料的抛物面结构,提出并且实现了一种适用于主流有限元软件的点阵材料抛物面结构的参数化建模方法。
通过编写程序自动化生成任意口径的由点阵材料构成的抛物面结构,实现几何建模、网格生成、约束和载荷条件施加的参数化工作。
同时可修改胞元拓扑形式和尺寸参数以便于优化,可根据约束的几何特征生成节点或者单元的约束集便于施加约束和载荷,可根据载荷的位置布置相应的作动器等,提高了建模的效率和质量,并为后续抛物面结构和点阵材料胞元的优化设计奠定了技术基础,具有一定的工程意义。
1点阵材料抛物面结构几何模型1.1手性六边形点阵材料性能简介本文涉及到的抛物面赋形重构变形形式主要为面外变形,而对于面外变形,应用负泊松比材料可以有效降低由高斯曲率变化产生的应力,作用原理是通过弯曲主导型点阵材料解耦了材料的弯曲应力和膜应力,从而扩大了材料的变形范围。
图1所示的手性六边形点阵材料就是这样一种负泊松比材料,这种点阵材料在面内变形时,等效泊松比为-1,且不同于其他已知的负泊松比材料,它的泊松比在相当大的应变范围内保持稳定,同时面内呈现2中胞元何参数获由手性六边形成抛物基于对手性六本文反射面的其几何模3所示。
由于文中涉及元从平面物面上时,抛物面上的最大胞元长度与最小胞元长度仅相差1.9%,说明抛物面上的胞元尺寸基本一致。
并且用这种点阵材料构成的抛物面中的拓扑胞元所形引起整个抛物面的宏观变形,故整个抛物面上的最大胞元和最小胞元在面积相差不大的情况下可以忽略这种微小差异,从而有利于在工程实践中加工生产以及在模拟仿真中快捷地参数化建模,而且通过平面映射方法也避免了其他曲面映射方法带来的不必要的建模和运算复杂的情况。
1.3由点阵胞元生成抛物面几何模型建立点阵材料抛物面结构的几何模型,首先要建立胞元的特征点。
如图4所示,一个典型的手性六边形胞元可以由12个特征点确定其基本形状,包括中心六边形的6个角点和6条三角形短边的外端点。
在基本胞元中,这12个特征点主要由胞元的六边形和三角形边长确定,其表达式如下:p1=原l原r2原3摇姨2r0蓘蓡;p2=原r2原3摇姨2r0蓘蓡;p3=r原l4原3摇姨4l0蓘蓡;p4=r2原3摇姨2r0杉删山山山山山山山山山煽闪衫衫衫衫衫衫衫衫衫;p5=l4+r2原3摇姨2l2原r蓸蔀摇0蓘蓡;p6=[r00];p7=p1+e1;p8=原p2;p9=p3+e1+e2;p10=原p4;p11=p5+e2;p12=原p6。
其中,r、l为分别为胞元内六边形边长及最大杆件长。
由特征点确定基本胞元后,可将其通过单位矢量e1和e2在抛物面的平面投影区域辐射阵列得到其他胞元的平面坐标,最后映射到抛物面上即可得该点阵材料的抛物面结构的基本几何模型。
图2胞元的几何尺寸图3抛物面几何模型及局部放大图图4基本胞元的特征点we2e1其辐射阵列的数学表达式为u j=u0+n j e1+m j e2。
其中:u0为基本胞元的特征点坐标;j为胞元的编号;u j为辐射胞元的特征点坐标;n j,m j分别为两个单位矢量的个数。
2参数化有限元建模方法本文基于共节点思想提出一种点阵材料抛物面结构的参数化有限元建模方法:1)首先确定胞元几何信息与节点的对应关系,其次根据胞元的几何特征确定胞元阵列的基本单位矢量方向,然后在目标域内阵列产生所需要的平面的点阵结构的节点和单元信息,最后通过映射生成点阵材料抛物面结构有限元模型;2)为方便定义载荷和约束条件以及计算有效域内的赋形精度,根据节点位置及编号和抛物面之间拓扑关系的数学表达式建立对应的节点集合。
