理论力学2—平面力系(习题课)
理论力学 平面任意力系例题

60
l
l
F
B
F
D
60
l
l D M
M
B
3l
G
F1
l MA
G FAy
x A FAx
17
A
q
例题
平面任意力系
2. 按图示坐标,列写平衡方程。
F
60
例 题 5
y l l D M
F F
x
0,
B
FAx F1 F sin 60 0
y
0,
FAy G F cos 60 0
M作用,梁的跨度为l,求固定端的约束力。
F
45
q
A l
M
B
14
例题
平面任意力系
q
A y
例 题 4
2. 列平衡方程
M
45
F
解: 1. 取梁为研究对象,受力分析如图
B
l
Fx 0,
Fy 0,
FAx F cos 45 0
FAy ql F sin 45 0
q FAx
力系对O点的主矩为
MO
O
主矢FR在第四象限内,与x轴的夹角为 –70.84o。M
O
M F
O
FRx
70.84
A
F1 3 m G1 1.5 m G2 3.9 m 2 355 kN m
FRy
FR
7
例题
平面任意力系
2. 求合力与基线OA的交点到O点的距离 x。 合力FR的大小和方向与主矢FR相同。 合力作用线位置由合力矩定理求得。
理论力学02习题课

M F d 1 2 F d 2ABC 2
平面内两个力偶,如果力偶矩相等,则两个力偶等效
8
主要内容和方法
平面力偶系的合成和平衡条件
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩的 代数和。
M FR d F1d F2 d M1 M 2
例题7:在刚体的A、B、C、D四点作用 有四个大小相等的力,此四力沿四个边 恰好组成封闭的力多边形,如图所示.此 刚体是否平衡?选择其中一对平行力, 同时改变方向,此刚体是否平衡? 答:图示情况下刚体不平衡,依然存在顺时针方向力矩,选择其 中一对平行力,同时改变方向,此时刚体平衡。
14
典型题目
例题8:在下面各图中,力或力偶对点A的矩都相等,它们引起的支座 约束力是否相同?
解:
F 0 F F 0 M 0 F l M 0
x A B A B
M M FA ; FB l l
23
作业题
2-12已知梁上作用有力偶,重量不计,在下面三种情况下,计算 之作的约束力
解:
F 0 F cos F cos 0 M 0 F l cos M 0
Fx 0 F FA
2 5 0 FA F 2 5
Fy 0 FD FA
19
1 1 0 FD F 2 5
支座A点的约束力与假设的方向相反
作业题
2-6如图所示,输电线重量沿AB均匀分布,求电线中点和两 端拉力 f 1m, AB 40m, P 400 N
0 M 2 F cos r2 0 M1 r cos r2 M 1 2 cos r1 r1
理论力学2—平面力系5
B
FCy
C
FCx
F A y FC y ( 2 ) 2 k N
q
M A (F ) 0 : M
A
FAx
ql 1 3 l FC y l FC x l 0
MA
A
FAy
2 3 F 4 kN
M
1 2
F Cx
M
A
6 kN m
2.5.4 平面桁架的内力计算
理想节点
桁架的实际节点
桁架是由杆件彼此在两端用铰链连接形 成的几何形状不变的结构。桁架中所有 杆件都在同一平面内的桁架称为平面桁 架。桁架中的铰链接头称为节点。
2.5.4 平面桁架的内力计算
为简化桁架计算,工程实际中采用以下几 个假设: (1)桁架的杆件都是直杆; (2)杆件用光滑铰链连接; (3)所受的力作用到节点上且在桁架平面内; (4)桁架杆件的重量略去不计,或平均分配在 杆件两端的节点上。 这样的桁架,称为理想桁架。其中的每根杆件都 只是在两端受力,因此所有的杆件都是二力杆。
2l 3
D
0
FDx F
F'Cy D
F Cx
2 3
F 4 kN
C F'Cx
求得结果为负说明与假设方向 相反。
M B FBx C FCx q FCy
2l/3
M
B l/2
A
C
F
FBy
F Cx
2 3
F 4 kN
D 2l/3 C F
FC y
M l
2 kN
M B l/2
F1 D F2
2 A
3 E n FE B
G FG
理论力学课后习题及答案解析

理论力学课后习题及答案解析文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-MG129]第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A 点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;将RB向下平移一段距离d,使满足:最后简化为一个力R,大小等于RB。
其几何意义是:R 的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力RA和一个力偶M A,且:如图所示;将RA向右平移一段距离d,使满足:最后简化为一个力R,大小等于RA。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学习题及解答1
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学第二章(2)

合力FR 的大小等于原力系的主矢
合力FR 的作用线位置
MO FR
小结:平面任意力系简化结果讨论
主矢
FR 0
FR 0
主矩
MO 0
MO 0 MO 0
MO 0
最后结果
说明
合力 合力作用线过简化中心
合力 合力偶
合力作用线距简化中心M O FR
与简化中心的位置无关
平衡
与简化中心的位置无关
21
简化为一个力:
c os (FR
,
i)
Fx FR
,
cos(FR ,
j)
Fy FR
原力系的主矢与简化中心O的位置无关
主矩: 原力系中各力对简化中心O之矩的代数和称为原力
系对点O的主矩。
n
M O M O (F1) M O (F2 ) ...... M O (Fn ) M o (Fi ) i 1
主矩与简化中心的选择有关
称点O为简化中心 F1’、F2’、….Fn’平面汇交力系,合力为FR’
M1、M2、….Mn平面力偶系,合力偶矩为MO
10
1、主矢和主矩
FR’=F1’+F2’+….+Fn’=F ’= F
主矢:量(简平称面为力主系矢中)所有各力的矢量和FR′称为该力系的主矢
主矢FR′的大小和方向余弦为:
FR (Fx )2 (Fy )2
11
平面任意力系向作用面内一点简化
一般力系(任意力系)向一点简化汇交力系+力偶系
(复杂力系)
(两个简单力系)
汇交力系 力偶系
力,FR‘(主矢) , (作用在简化中心)
力偶 ,MO (主矩) , (作用在该平面上)
理论力学第2章平面任意力系
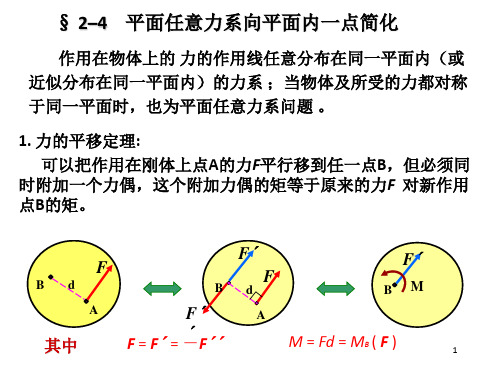
空载时轨道A 、 B的约束反力,并问此起重机在使用过程中有无翻
倒的危险。
解:
(1)起重机受力图如图
(2)列平衡方程 :
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
(1)FR´= 0,Mo ≠ 0, (2)FR´ ≠ 0,Mo = 0, (3)FR´≠ 0,Mo ≠ 0, (4)FR´= 0,Mo = 0,
合力偶,合力偶矩,MO MO (Fi )
合力,合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用,如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解:T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0
理论力学02平面力系的简化和平衡

第二章
平面力系的简化和平衡
2.1力的合成与分解: 1.平行四边形法则: 作用于物体上同一点的两个力可合成 一个合力,此合力也作用于该点,合力的 大小和方向由以原两力矢为邻边所构成的 平行四边形的对角线来表示。
④ R ≠0, MO ≠0,为最一般的情况。此种情况还可以继续简 化为一个合力 R 。
合力R 的大小等于原力系的主矢 合力R 的作用线到简化中心的距离
MO d R
结论:
平面任意力系的简化结果 :①合力偶MO ; ②合力 合力矩定理:由于主矩 而合力对O点的矩
R
M O mO ( Fi )
主矩:
M O M O ( F ) 3F1 1.5P 1 3.9P 2 2355kN m
(2)求合力及其作用线位置:
d x 3.514m 0 0 cos 90 70.84
(3)求合力作用线方程:
MO MO
' ' FR x FRy y FRx x FRy y FRx
二、汇交力系的合成 由几何法知合力等于各分力的矢量和,即
R F Fn F i 1 F 2 F 3
又 由于
Fi X ii Yi j Zi k Fxii Fyi j Fzi k
代入上式得 R
F i F
xi
yi
j Fzi k
根据合矢量投影定理得合力在坐标轴的投影
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MD(F) 0 :
FBl FE1
2 2
l
0
F'Dy F'Dx
FE1
2
2 3
P
D FE1
E
MC (F) 0 :
FAxl FE2
FAxl
FAyl
FEx
l 2
FEy
l 2
0
联立求解以上两方程即得同样结果。
类似地, 亦可以BDC和BD为研究 对象, 进行求解。
FDy 2l/3 P
FDx D
C
E
F'Ex
FAy A
FAx F'Ey
F'Cx
C
F'Ex
F'Cy
E
FAy A
FAx F'Ey
方法3: 分别以BD和AC为研究对象, 受力如图。
a
FDa
1 2
q(2a
b)2
0
FAy
q
解之得:
q(2a b)2 FD 2a
FAx
q(2a 2a
b)2
FAx FD
AE 23
D1 C
F
B
FAy q(2a b)
例4
(2) 再以销钉C为研究对象,受力
如图,建立如图坐标。
y
Fx 0 : F1 F3 cos 45o 0 F1 Fy 0 : F2 F3 sin 45o 0
FCx
FAx
1 2
ql
0
FAx
FCx
1 2
ql
(4) 1 3 2 1 kN 2
M
B
FBx FBy
FCy C
FCx
M
B
FCy C
FCx
q
MA
FAx A FAy
Fy 0 : FAy FCy 0
M
B
FCy C
FCx
FAy FCy (2) 2 kN
qa 2
FABy F qa
q
FD M
3a a
4. 取AB(不含销钉)
Fx 0 :
FAx
FABx
3qa 2
0
FAx qa 方向向左
B
C
aa
Fy 0 : FAy FABy 0 FAy F qa
A q
B
F'ABx
M A(F) 0 :
F'ABy
F
D M
q
3a a
载荷分布及尺寸如图。
BC
销钉B穿透AB及BC两构
aa
件, 在销钉B上作用一铅
垂力F。已知q, a, M, 且
A
M=qa2。求固定端A的 q
约束力及销钉B对AB杆
及BC杆的作用力。
3a a
解: 1. 取BC(不含销钉B)分析
MC (F) 0 :
F
D M
q
BC aa
M FBCy a 0 M
M
A
3qa 2
3a 3
FABx
3a
FABy
a
0
FAy
M A Fa qa2
q
A
MA
FAx
a
课堂作业:试求固定端A和铰支座
F
D
B的约束力。其中 CE=ED
E
q0
C
30°
M B
解: 先以BD为研究对象, 受力 如图。
3a
M D (F ) 0 : FBx a M 0
是AB、BC中点, 求绳EF的张力。
解: 1) 以DC为研究对象, 受
AE
B
力如图。
F
MC (F) 0 :
D C
FDy l
W
l 2
0
FDy
W 2
(1)
FDy FDx D
W
FCy
C
FCx
2) 再以整体为研究对象:
Fy 0 :
FAy FDy 3W 0 (2)
FAy 2.5W
q
D
C
M
a
A
B
a
解: 1)取
q
CD研究 D
FDx
FDy
C
FCx FCy
MC (F) 0 :
qa2 2
FDy
a
0
FDy
qa 2
2)取 BCD M B (F ) 0 :
qa2 2 FDy a FDx a M 0
FDx qa
q
D
C
M
A
B
a
q
D
C
FDx
M
F
2l 3
0
D FDx
FCx
2 3
F
4
kN
CF
F'Cx
求得结果为负说明与假设方向 相反。
F'Cy D
2l/3
M
FCy
B
C
M
B
CF
FBx
FCx
FBy
l/2
q
A
FCx
2 3
F
4
kN
M
D
2l/3
FCy l 2 kN M
B
C
F
l/2
q
A
(3) 取AB连同BC分析
Fx 0 :
解之得:
FAx
M a
3 2
q0a
A
FAx
MA FAy
FDx FDy
D M
FAy
F 2
3M 3a
M A 3q0a2 3M
FBx
B
FBy
习题课5 由直角曲杆ABC、DE, 直杆CD及滑轮组成的结构
如图所示, 杆AB上作用有水平均布载荷q。不计各构件的重量, 在D处作用一铅垂力F, 在滑轮上悬吊一重为P的重物, 滑轮的半 径r=a, 且P=2F, CO=OD。求支座E及固定端A的约束力。 解: DE是二力构件,支座E的 约束力沿ED连线方向。
FGy
力如图。
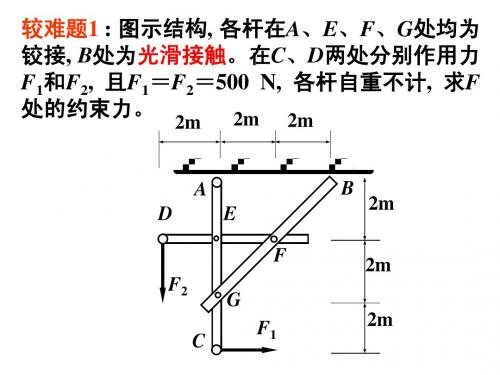
2m 2m 2m
F F'Fx FGx
G
MG (F) 0 : 4FB 2FFy 2FFx 0
解得: FFx 1500 N
A DE
F
F2 G
C
F1
B 2m
FB 1000N
2m
2m
习题课4 : 三根等长同重均质杆(重W )如图在铅
垂面内以铰链和绳EF构成正方形。已知: E、F
MA
FAx
FAy P F FE cos 45o 0
FAy 2F
M A(F) 0 :
MA q6a3a P(4.5a r) FE 6 2a F 6a 0
M A 5aF 18qa2
习题课6 : 三无重杆AC、BD、CD如
P 2l/3
图铰接, B处为光滑接触, ABCD为正方形, 在CD杆距C三分之一处作用一垂直力P, D
F2 F3 45° x
C
F1 FD
F3
q(2a b)2 2a
F2
q(2a 2a
b)2
q
AE
F
B
a
23
D1
C
b
a
a
习题课2: 两根铅直杆AB、CD与水平杆BC铰接,
B、C、D均为光滑铰链, A为固定端, 各杆的长度
均为l=2 m, 受力情况如图所示。已知水平力F
=6 kN, M=4 kN·m, q=3 kN/m。求固定端A及
q
MA
M A(F) 0 :
FAx A FAy
11
M
A
M
2
ql
l 3
FCy
l
FCx
l
0
FCx
2 3
F
4
kN
M A 6 kN m
FCy
M l
2 kN
求得结果为负说明与假设方向相反, 即为顺时针 方向。
习题课3 : 图示结构, 各杆在A、E、F、G处均为
方法1: 先以DC为研究对象
FDy 2l/3
M D (F )
0:
FCy
l
P
2l 3
0
FDx D
P FCy C FCx
FCy
2 3
P
再以BDC为研究对象
2l/3 P FCy
Fy 0 : FEy FB FCy P 0
FEy
1 3
P
方向向下
MC
(F )
0
:
FEx
1)取CD、DE带滑轮分析:
MC (F) 0 :
FT r FE 3 2a F 3a P (1.5a r) 0
FT P
FT
FE 2F
FCx
FCy
FE
2)取整体分析:
Fx 0 :
FAx 6qa FE cos 45o 0
FAy
