中文版-实验模态分析简化版
【工程测试与信号处理课件】实验模态分析

测点布置 (1)能够较好地反映结构物的构型 (2)能够充分显示结构的模态振型 例:一个梁单元无法求解简支梁的10个模态。计算上一般要求 至少20个单元,计算出的20阶模态,只有前10阶准确。 激励点 应避开节点节线。多点激励进行校核。 激励力的选择 在不破坏试件的情况下,尽可能大的激励力,有助于提高 信噪比。 不同大小的激励力,可以定性考查结构非线性的程度
(2)传感器标定;
(3)将试验结构以适当方式支撑起来; (4)选择适当方式激励试验结构; (5)通过拾振系统测量、记录下激励和响应的时间历程。
2.1 试验结构的支撑
试验的目的决定了试验的支撑条件。试验目的主要有三种情况: 与有限元模型进行比较;在常规工作条件下测量试件的动态特 性;对规定边界条件下的子结构进行试验研究,使之与整体结 构相适应。 与试验目的对应的支撑条件一般有自由支撑、固定支撑和原装 支撑三种。 (1)自由支承(Free-Free Support)。 无约束条件对仿真计算容易实现,但需要进行移频处理。试 验实现真正自由支承的方法有:气悬浮、磁悬浮、太空无重力 环境、自由下落(失重)。
4.系统(参数)识别
4.1频域方法的模态参数识别 根据观测到的输入输出数据建立系统的数学模型,并要求这 个数学模型按照一定准则,尽可能精确地反映系统动态特性, 称系统识别。如果系统的数学模型能用一定数量的参数描述, 那么系统识别便成为参数识别,有称参数辨识或参数估计。 模态参数识别的方法分为直接估计法和曲线拟合法。直接估 计法认为系统的观测数据是准确的,没有噪声和误差,直接 由观测数据求取系统的数学模型。
激振器的支撑: (1)固支在结构物外。 (2)悬挂在结构物外(低频)。 因使激振器悬挂系统的频率远低于结构的激励和弹性体共 振频率。必要时可在激振器上附加大的质量块以进一步降 低悬挂频率。 (3)采用隔振悬挂在结构物内部。
模态分析实验报告

模态分析实验报告1.引言模态分析是一种常用的结构动力学方法,旨在研究结构在不同频率下的振动特性,对于结构设计和加固具有重要意义。
本实验旨在通过模态分析方法,研究一个简单的结构体系的固有频率和振型。
2.实验目标通过实验测量和计算,得到结构的第一、第二和第三固有频率,并利用模态分析方法绘制结构的振型图。
同时,通过实验结果对比,验证模态分析方法的有效性。
3.实验材料和方法(1)材料:实验所用的结构是一个简单的桥梁模型,由若干根长木棒组成。
(2)方法:悬挂测频仪对结构进行激振,通过麦克风捕捉振动信号,并用计算机进行分析和处理。
4.实验过程(1)组装结构体系:根据实验设计要求,组装简单桥梁模型,确保结构的稳定性和一致性。
(2)悬挂测频仪:将测频仪正确安装在结构体系的一侧,并调整好位置和角度。
(3)激振:根据测频仪的说明书,调节激振源的频率和幅值,使结构产生振动。
(4)数据记录:用麦克风将振动信号转化为电信号,并通过计算机采集和记录数据。
(5)模态分析:利用采集的数据,进行模态分析,计算结构的固有频率和振型。
(6)数据处理:整理和分析实验结果,绘制振型图并与理论值进行比较。
5.结果分析通过实验和数据处理,得到结构的第一、第二和第三固有频率分别为f1、f2和f3、根据模态分析方法,绘制结构的振型图。
将实验结果与理论值进行比较,进行误差分析、灵敏度分析等。
6.结论本实验利用模态分析方法,研究了一个简单的结构体系的固有频率和振型,并通过实验结果与理论值的比较,验证了模态分析方法的有效性。
通过本实验,我们更深入地理解了结构振动的基本原理和方法,具备了一定的模态分析实验技能。
7.实验总结本实验通过模态分析方法研究了结构的振动特性,对于结构设计和加固具有重要意义。
在实验过程中,我们遇到了一些困难和问题,通过积极探索和思考,取得了一定的实验成果。
但我们也发现了许多不足之处,如实验设计和数据处理的精确性等,需要进一步改进和完善。
结构模态分析实验报告

结构模态分析实验报告1. 引言在结构工程领域中,结构模态分析是一种重要的分析方法,旨在研究和了解结构的固有特性,包括自然频率、振型和阻尼等。
通过模态分析,我们可以评估结构的稳定性、安全性以及对外界激励的响应能力。
本实验旨在通过模态分析方法对某一结构进行测试和分析,以获取结构的模态参数。
2. 实验设备和方法2.1 实验设备本实验使用的设备包括: - 振动台:用于提供激励力的设备。
- 振动传感器:用于测量结构的振动响应。
- 数据采集系统:用于采集传感器测量到的数据。
2.2 实验方法本实验采用以下步骤进行结构模态分析: 1. 确定实验对象:选择待测试的结构,并对其进行准备,如清洁表面、固定传感器等。
2. 安装传感器:将振动传感器安装在结构的关键位置,以测量结构的振动响应。
3. 准备振动台:调整振动台的参数,如频率、振幅等,以提供适当的激励力。
4. 开始振动测试:启动振动台,通过施加激励力对结构进行振动,并同时采集传感器的数据。
5. 数据分析:利用数据采集系统获取的数据,进行模态分析,计算结构的自然频率、振型等参数。
6.结果分析:根据计算得到的模态参数,对结构的稳定性和响应能力进行评估。
3. 实验结果通过实验和数据分析,我们得到了以下结构的模态参数: - 自然频率1:X Hz - 自然频率2:Y Hz - 自然频率3:Z Hz同时,我们还得到了结构的振型图,描述了结构在不同振动频率下的振动形态。
4. 结果分析根据实验结果,我们可以对结构的稳定性和响应能力进行初步评估。
通过比较得到的自然频率和已知的设计要求,我们可以判断结构是否存在共振现象;通过分析振型图,我们可以了解结构在不同振动频率下的振动特点。
5. 结论本实验通过结构模态分析方法,获取了待测试结构的模态参数,并对其稳定性和响应能力进行了初步评估。
实验结果表明,该结构在给定的激励条件下表现出良好的稳定性和响应能力。
这些结果对于结构的设计和改进具有重要的参考价值。
中文版-实验模态分析简化版
Time weighting
Overload indication
BA 7679-16, 27
智能型传感器使得设置极其方便
内置的TEDS( read/write Transducer Electronic Data Sheet ) 芯片, 存储在芯片中的传感器参数可以被 TEDS兼容的系统使用,例如 PULSE™
Output
Time Domain
Inverse FFT
Frequency Response H1(Response,Excitation) - Input (Magnitude) [(m/s?/N] Working : Input : Input : FFT Analyzer 10
10m 1m 0 200 400 600 800 [Hz] 1k 1,2k 1,4k 1,6k
l da ain Mo om iew D V
BA 7679-16, 20
曲线拟合提取模态参数
单自由度方法 (SDOF)
简单结构 少数且分隔较开的模态
多自由度方法 (MDOF)
ω0
Frequency Response H1(Response,Excitation) - Input (Magnitude) [(m/s?/N] Working : Input : Input : FFT Analyzer 10
多个模态 大量且频率接近的模态
局部
基于单一自由度
100m
全局
0 200 400 600 800 [Hz] 1k 1,2k 1,4k 1,6k
基于多个自由度
单参考
基于频响函数矩阵的一行或者一列
多参考 基于频响函数矩阵的多行或者多列
对称结构在同一频率呈现多个模态 一个峰值不一定只意味着一个模态
模态分析实验报告

《机械工程测试技术》综合实验报告实验项目名称:机械结构固有模态实验班级:机械32实验小组成员姓名(学号):张豪47 张唯48赵亮49 景世钊33王汝之42 朱金格28实验小组组长:张豪实验报告日期: 15/12/12实验目的:针对机械结构(简支梁、悬臂梁、圆盘)的固有模态进行分析,了解几种常用的结构动态特性激励方法,掌握机械结构固有模态的测试系统设计、测试系统搭建、数据采集及信号分析方法和技术。
实验原理:模态分析方法及其应用:模态分析方法是把复杂的实际结构简化成模态模型,来进行系统的参数识别(系统识别),从而大大地简化了系统的数学运算。
通过实验测得实际响应来寻示相应的模型或调整预想的模型参数,使其成为实际结构的最佳描述。
主要应用有:用于振动测量和结构动力学分析。
可测得比较精确的固有频率、模态振型、模态阻尼、模态质量和模态刚度。
可用模态实验结果去指导有限元理论模型的修正,使计算模型更趋完善和合理。
用来进行结构动力学修改、灵敏度分析和反问题的计算。
用来进行响应计算和载荷识别。
模态分析基本原理:工程实际中的振动系统都是连续弹性体,其质量与刚度具有分布的性质,只有掌握无限多个点,在每瞬时的运动情况,才能全面描述系统的振动。
因此,理论上它们都属于无限多自由度的系统,需要用连续模型才能加以描述。
但实际上不可能这样做,通常采用简化的方法,归结为有限个自由度的模型来进行分析,即将系统抽象为由一些集中质块和弹性元件组成的模型。
模态分析是在承认实际结构可以运用所谓“模态模型”来描述其动态响应的条件下,通过实验数据的处理和分析,寻求其“模态参数”,是一种参数识别的方法。
模态分析的实质,是一种坐标转换。
其目的在于把原在物理坐标系统中描述的响应向量,放到所谓“模态坐标系统”中来描述。
这一坐标系统的每一个基向量恰是振动系统的一个特征向量。
也就是说在这个坐标下,振动方程是一组互无耦合的方程,分别描述振动系统的各阶振动形式,每个坐标均可单独求解,得到系统的某阶结构参数。
模态分析实验报告一

实验一用不测力模态分析法测量简支梁的模态参数、实验目的(1)学习不测力实验模态分析方法的原理(2)掌握用不测力模态分析法测量结构固有频率、模态振型、模态阻尼比的方法、实验系统框图三、实验原理所谓不测力法就是在试验过程中不需要测量激励力的方法。
工程中的的大量结构和机器都是很难人工施加激励力的。
其结构的响应主要由环境激励引起的,而这些环境激励是既不可控又难以测量的。
不测力法只能利用系统的响应数据对固有频率、模态振型、模态阻尼或阻尼比这几个模态参数进行估计,而这几个模态参数已经能够满足绝大多数工程中结果动力特性分析的要求。
不测力法模态软件利用测量得到相应的自功率谱、互功率谱、传递率和相干函数进行模态参数估计。
前述的运行模态分析法(OMA属于不测力模态分析法。
不测力法也可分为解析法和图解法两种类型。
使用范围与测力法一致。
图解法也可选用自互功率谱综合法或传递函数法,解析法可选用随机子空间法(SSI)。
四、实验步骤简支梁的几何尺寸为:长(x向)625mm宽(y向)50mm使用不测力法做其z方向的的振动模态,实验过程如下。
1. 测点的确定可以将简支梁分出八等分,即九个结点,去掉两端的两个节点以及2号节点,共选取6个测点,如图所示。
实验时,将传感器放置于每一个等分点处。
2. 连接仪器将两个测量用的加速度传感器分别接入采集器的的通道1和通道23. 测量设置打开仪器电源,启动分析软件,选择频谱分析模式。
新建4个窗口,分别显示通道1和通道2的时间波形以及通道1和通道2的平均谱,平衡清零后,即可开始采样。
4. 参数设置(1)系统参数设置:采样频率:2kH z;采样方式:连续;触发方式:自由采集;平均方式:线性平均;平均次数:100次;时域点数:2048点;窗类型:海宁窗•(2)通道参数设置:参考通道:通道1。
工程单位和灵敏度:参考实验十。
本实验中,两个传感器的灵敏度必须设置正确。
模态参数:编写测点号和方向。
实验时,将其中一个传感器放置在参考点处,并在整个测试过程中该传感器位置不变,其通道的“几何参数(模态参数)”栏中“参考标识”打“V”,其余通道的“参考标识”打“X”;移动另外一个传感器进行测量,在每一批次的测试过程结束之后,都要对通道2的测点编号进行设置,具体做法与测力模态分法相似。
模态分析报告【范本模板】

汽车挡风玻璃模态试验报告(模态分析理论与试验第三小组)**: **小组:三组学号:*******目录1 试验目的 (3)2 试验仪器 (3)3 试验对象 (3)4 试验测量和分析系统 (4)5 实验原理 (5)5.1 传递函数 (5)5.2 相干函数 (5)5.3 误差控制 (6)6 模态分析方法和测试过程 (7)6.1 激励方法 (7)6 .2 结构安装方式 (7)7、实验步骤 (8)7.1测点的确定 (8)7.2 仪器连接 (9)7.3 结构生成及约束 (9)7.4 参数设置与采样 (9)7.5实验数据分析处理 (10)8、实验结果和分析 (13)8.1 模态频率和阻尼 (13)8.2 试验与仿真对比 (18)8.3 分析结论 (21)1 试验目的1。
学习模态分析原理和模态测试方法;2。
试验分析得到汽车挡风玻璃的前15阶模态的模态参数;3.试验分析汽车挡风玻璃的动态振动特性;4。
为汽车挡风玻璃的有限元分析计算模型的修改提供可靠依据.2 试验仪器试验仪器如表1所示:表1 试验仪器列表3 试验对象试验对象:POLO三厢车前挡风玻璃.实验对象附件描述见表2表2 实验对象描述4 试验测量和分析系统试验测量分析系统由三大部分组成:试验试验激振系统,响应采集系统,模态分析和处理系统。
其中,(1) 试验激振系统包括:江苏联能LC系列力锤;(2) 响应采集系统包括加速度传感器、和DASP信号采集系统;(3)模态分析和处理系统主要是DASP和Matlab软件。
具体的组成方式如图1和图2所示。
图1模态试验测量分析系统模型示意图图2模态试验测量分析系统-电荷放大器图3模态试验测量分析系统—INV 306U DASP数采系统5 实验原理5。
1 传递函数试验模态分析是基于系统响应和激振力的动态测试,即通过振动测试,经信号处理和参数识别确定系统的模态参数,建立以模态参数表示的运动方程.从模态分析理论可知,这些参数可以通过传递函数或频响函数曲线进行分析求得。
实验模态分析

二、频响函数的测量
3 试件及激振器的支撑 激振器: 1.固支在结构物外。 2.悬挂在结构物外(低频)。 因使激振器悬挂系统的频率远低于结构的激励和弹性体共振频率。必 要时可在激振器上附加大的质量块以进一步降低悬挂频率。 3.采用隔振悬挂在结构物内部。
二、频响函数的测量
二、频响函数的测量
4 测点布置与激振点的选择 测点布置 1.能够较好地反映结构物的构型 2.能够充分显示结构的模态振型 例:一个梁单元无法求解简支梁的10个模态。计算上一般要求至 少20个单元,计算出的20阶模态,只有前10阶准确。 激励点 应避开节点节线。多点激励进行校合。 激励力的选择 在不破坏试件的情况下,尽可能大的激励力,有助于提高信噪 比。 不同大小的激励力,可以定性考查结构非线性的程度
三、曲线拟合方法
频域方法:基于FRFs数据的方法 经典方法,分析仪厂商自65年起开发。如美国HP系列分析 仪:3560、35665、35670、3565s、5423等;丹麦 B&K公 司的模拟分析仪;SISO、SIMO、MIMO识别方法; 最小二乘频域法LSFD 结构系统参数识别ISSPA 复模态指数函数CMIF 利用输入和输出数据进行模态参数识别: 单输入/单输出识别法(SISO) 单输入/单输出识别法(SIMO) 多输入/多输出识别法(MIMO)
二、频响函数的测量
3 试件及激振器的支撑 2.固支支承(Fixed-Fixed Support)。又称地面支承。 理论上容易实现,仿真计算时只需要将有关自由度约束即可。但 实现起来有困难。由于实现固支条件的结构不可能是刚性的,有弹 性。因此要实现固支支承,就必须要求支承结构的最低弹性体频率远 高于试验结构的最高分析频率。因此要实现高频模态的固支支承是很 困难的,一般情况下,中小结构能够实现的固支频率大约是400Hz, 特殊条件下小结构固支有可能超过1000Hz,但对大结构要实现固支 支承很困难。 3.实际工作状态支承。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一般的留数: Rijr = a ·yir ·yjr Beam
Force
原点(驱动点)留数: Riir = a ·yir2 原点留数用于缩放模态模 型
BA 7679-16, 19
提取模态振型
Amplitude
First Mode
Second Mode
Third Mode Beam Acceleration
1 00m
全局
0 200 400 600 800 [Hz] 1 k 1 ,2k 1 ,4k 1 ,6k
单参考
基于频响函数矩阵的一行或者一列
多参考 基于频响函数矩阵的多行或者多列
BA 7679-16, 21
对称结构在同一频率呈现多个模态 一个峰值不一定只意味着一个模态
模态测试
什么是模态测试 为什么做模态测试 怎么做模态测试
2. 测量
3. 曲线拟合
4. 验证
BA 7679-16, 15
频率响应函数
[m/s 瞉 Time(Res po nse) - Input Wo rk ing : Input : Input : FFT A nalyzer 80 40 0
-40 -80 0 40m 80m 1 20m [s ] 1 60m 200m 240m
SDM and FRS (基于验证的模态模型)
仿真“假如。则 。”
结构动力学修改(Structural Dynamics Modification)
质量修改
刚度修改
动力吸振器 移动共振频率 High response Low response Previous response
强迫响应仿真分析
PULSE™
2. 测量
3. 曲线拟合
4. 验证
BA 7679-16, 23
ME‟scope 或者 I„DEAS
PULSE 模态测试顾问(Modal Test Consultant)
Vibration Data
Modal Test Consultant
Modal
File Transfer
当结构受到一个或者多个激励时动力 学行为会怎样?
BA 7679-16, 13
模态测试 什么是模态测试 为什么做模态测试
怎么做模态测试
Brüel & Kjæ r 的解决方案
BA 7679-16, 14
怎么做模态测试
1. 建模
建立几何模型 定义自由度 确定测量方向 频率响应函数 力锤或者激振器激励 定义相干函数,自谱等用于验证 频率 阻尼 留数 (模态振型) MAC (模态置信准则) 模态置信因子 相位分布 模态参与因子 ........
Force Force Force Force Force Force Force Force Force Force Force Force
BA 7679-16, 20
曲线拟合提取模态参数
单自由度方法 (SDOF)
简单结构 少数且分隔较开的模态 多个模态 大量且频率接近的模态
多自由度方法 (MDOF)
阻尼比:
f0
1 T
w0
BA 7679-16, 18
模态模型 – 局部参数
留数在每一个DOF被单独描述 (局部) 留数: 模态的 “强度”
Hw0 2
Amplitude First Mode
Second Mode
Third Mode
w0 留数: R = H(w0) ·
Hale Waihona Puke FrequencyBA 7679-16, 26
PULSE 模态测试顾问
设置和测量
Mounting the transducer
显示器上的几何模型指导传感 器的安装 参量参数的图形化设置 测量状态的声音和视觉通知
Geometry model on screen
自动的标签DOF – label while measuring
BA 7679-16, 17
模态模型 – 全局参数
固有频率和模态阻尼是动力学模型所有自由度的共同特征 (全局) 频域 时域
1 Decay Rate = t
Time
3dB
3 dB bandwidth =2
w0
Frequency
T
t
固有频率: 阻尼比:
w0 = 2pf0
w0
固有频率:
模态测试
什么是模态测试
为什么做模态测试
怎么做模态测试 Brüel & Kjæ r 的解决方案
BA 7679-16, 10
为什么做模态测试
改进有限元模型
– 在原形样机上通过测试进行验证 – 通过引入阻尼来改进有限元模型
故障诊断
– 降低过大的振动水平 – 确保共振远离激励频率
仿真“假如。则。。”
F requenc y Respo ns e H1 (Respo ns e,Excitatio n) - Input (M agnitude) Wo rk ing : Input : Input : F FT A nalyzer
[(m/s ?/ N/ s] 2k
Impulse Res pons e h1(Respo nse,Exc itation) --Input (Real P art )) h1 (Res po nse,Exc itation) Input (Real P art Wo rk ing : Input : Input :: FFT A nalyzer Input F FT A nalyzer
1. 创建几何模型
简便易用的 几何建模工 具 可以利用DXF, STR 和 UFF 文件格式输入几何 模型
2. 定义测试模型
给几何模型分配自由度
3. 输出
几何模型 DOF信息 (测量结果)
包括 面和隐藏的线
BA 7679-16, 30
很容易设置力锤激励
在大量不同的位置敲击被测物体
1 自定义量程 或者 选择输入量程
w0
[(m/s ?/ N] F requenc y Respo ns e H1 (Respo ns e,Excitatio n) - Input (M agnitude) Wo rk ing : Input : Input : F FT A nalyzer 1 0
局部
基于单一自由度 基于多个自由度
Software
PULSE
BA 7679-16, 24
PULSE 模态测试顾问
Setup Calibration Measurement
特征和优点 导引化 测量 几何驱动的 测量
– 可以使用从CAD输入几何选项
分析仪参数的直观图形控制 显著降低了设置和测量时间 降低了人为错误风险 自定义能力
– 确定载荷 – 复杂激励下结构的响应 – 结构动力学修改
结构综合分析
– 预测组装子部件或总成的动力学行为
模态测试
首先利用在飞机工业 今天也广泛的应用于汽车工业和许多其他工业
BA 7679-16, 11
故障诊断
频率响应函数
High responses 运行时的振动响应
BA 7679-16, 12
2 选择 触发水平
敲击被测物体一次 3 选择时间 计权窗
4 设置 预触发
BA 7679-16, 31
PULSE 模态测试顾问
几何模型 导引测量
Input
1 k
0
-1k
-2k 0 40m 80m 1 20m [s ] 1 60m 200m 240m
1 00m
1 0m
1 m
1 00u 0 200 400 600 800 [Hz] 1 k 1 ,2k 1 ,4k 1 ,6k
Frequency Response Function
Impulse Response Function
有限元建模 FEM 预测测试模型 阻尼数据
模态测试
模态模型的 对比和验证
结果 验证
曲线 拟合
测试 有效性 验证
更新 最终模型 仿真预测: “假如。那么。。”
BA 7679-16, 8
故障诊断
有限元 vs 测试模型
发动机缸体的扭转模态
MAC
448 Hz FEA
459 Hz
EMA
BA 7679-16, 9
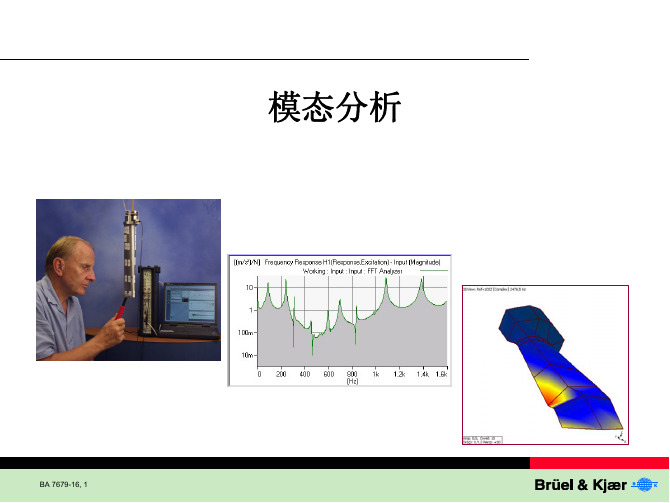
模态分析
BA 7679-16, 1
引言 2
当今需求: 运行的速度越来越快 对燃油经济性要求越来越高 结构越来越轻量化 这些需求要求降低结构重量 结果: 结构变得越来越“弱” 共振频率向激励得频率范围移动 由于动态载荷得存在结构将更容易“失效 ”
BA 7679-16, 3
引言 3
[N] 200
Time(Exc itatio n) - Input Wo rk ing : Input : Input : FFT A nalyzer
FFT
200m 240m
1 00
0
-100
-200 0 40m 80m 1 20m [s ] 1 60m
Output Motion Response H(w) = = = Input Force Excitation
模态参数
理论分析人员利用有限元建 模来获得 – 特征值 – (阻尼) – 特征向量 实验分析人员利用模态测试 来获得: – 固有频率 – 阻尼比 – 模态振型
