数学建模第二次作业
《第三章 数学建模活动(二)》试卷及答案_高中数学必修_北师大版_2024-2025学年

《第三章数学建模活动(二)》试卷(答案在后面)一、单选题(本大题有8小题,每小题5分,共40分)1、某工厂生产一批产品,原计划每天生产100件,10天完成。
后来由于提高效率,每天多生产了20件,实际用了8天完成。
设提高效率后每天生产的件数为x件,那么x的值是:A、60B、80C、100D、1202、在解决实际问题时,建立数学模型的一般步骤不包括以下哪一项?()A. 确定问题背景和目标B. 收集和整理数据C. 建立数学模型D. 进行实验验证3、某工厂生产一批产品,已知生产这种产品需要原材料A和B,其中原材料A的用量与原材料B的用量成比例。
若生产100个产品需要原材料A和原材料B分别为10kg 和20kg,那么生产200个产品需要原材料A和原材料B分别为多少kg?A、20kg和40kgB、30kg和60kgC、40kg和80kgD、50kg和100kg4、在解决数学建模问题时,以下哪项步骤是错误的?A、明确问题背景和目标B、建立数学模型C、收集和分析数据D、求解数学模型,得到结果但不进行验证5、某工厂计划生产一批产品,已知生产这批产品需要投入的原材料费用为3000元,人工费用为1000元,其他费用为500元。
如果每件产品的利润为10元,要使得利润总额达到10000元,至少需要生产多少件产品?A. 500件B. 1000件C. 1500件D. 2000件6、在解决数学建模问题时,以下哪种方法不是常用的策略?()A、建立数学模型B、分析模型,提出假设C、进行数据收集和整理D、进行数学推导,得出结论7、某市为了改善交通状况,计划在一条长为10公里的主干道上增设若干个公交站点。
根据交通流量分析,每两个站点之间的平均距离不宜小于1公里也不宜大于2公里。
如果这条主干道的起点和终点都设有一个站点,那么最多可以设置多少个站点?最少可以设置多少个站点?A. 最多11个站点,最少6个站点B. 最多12个站点,最少5个站点C. 最多11个站点,最少5个站点D. 最多10个站点,最少6个站点8、下列关于函数模型y=ae^(bx)+c(a、b、c为常数,且a>0,b≠0)的说法中,正确的是:A. 当a=1,b=0,c=0时,该函数表示一个常数函数B. 当a=1,b=1,c=0时,该函数表示一个指数函数C. 当a=1,b=0,c=1时,该函数表示一个一次函数D. 当a=1,b=-1,c=1时,该函数表示一个二次函数二、多选题(本大题有3小题,每小题6分,共18分)1、以下哪些选项属于数学建模的基本步骤?()A. 提出问题B. 收集数据C. 建立模型D. 求解模型E. 验证模型F. 模型应用2、某工厂为了提高产品质量,计划对生产流程进行优化。
福师《数学建模》在线作业二1答案

福师《数学建模》在线作业二-0002试卷总分:100 得分:0一、判断题(共40 道试题,共80 分)1.最小二乘法估计是常见的回归模型参数估计方法A.错误B.正确正确答案:B2.我国对异常值没有颁布标准A.错误B.正确正确答案:A3.测试分析将研究对象视为一个白箱系统A.错误B.正确正确答案:A4.建模过程仅仅是建立数学表达式A.错误B.正确正确答案:A5.对实际问题建模没有确定的模式A.错误B.正确正确答案:B6.关联词联想法属于发散思维方法A.错误B.正确正确答案:B7.整个数学建模过程是又若干个有明显区别的阶段性工作组成A.错误B.正确正确答案:B8.建模主题任务是整个工作的核心部分A.错误B.正确正确答案:B9.利用乘同余法可以产生随机数A.错误B.正确正确答案:B10.数学建模是一种抽象的模拟,它用数学符号等刻画客观事物的本质属性A.错误B.正确正确答案:B11.附录是正文的补充A.错误B.正确正确答案:B12.利用理论分布基于对问题的实际假设选择适当的理论分布可以对随机变量进行模拟A.错误B.正确正确答案:B13.求常微分方程的基本思想是将方程离散化转化为递推公式以求出函数值A.错误B.正确正确答案:B14.相对误差等于绝对误差加测量误差A.错误B.正确正确答案:A15.在解决实际问题时经常对随机现象进行模拟A.错误B.正确正确答案:B16.模型不具有转移性A.错误B.正确正确答案:A17.图示法是一种简单易行的方法A.错误B.正确正确答案:B18.样本平均值和理论均值不属于参数检验方法A.错误B.正确正确答案:A19.数学建模仅仅设计变量A.错误B.正确正确答案:A20.数学建模不是一个创新的过程A.错误B.正确正确答案:A21.拐角问题来源于医院手术室病人的接送A.错误B.正确正确答案:B22.数据也是问题初态的重要部分A.错误B.正确正确答案:B23.人口预测模型用以预测人口的增长A.错误B.正确正确答案:B24.泊松分布常用于穿越公路模型中A.错误B.正确正确答案:B25.数学建模中常遇到微分方程的建立问题A.错误B.正确正确答案:B26.利用偏回归平方和评价一个自变量在一组自变量中的重要性A.错误B.正确正确答案:B27.数据变量呈现很强随机性的数据为随机数据A.错误B.正确正确答案:B28.利润受销售量的影响和控制A.错误B.正确正确答案:B29.明显歪曲实验结果的误差为过失误差A.错误B.正确正确答案:B30.回归分析是研究变量间相关关系的统计方法A.错误B.正确正确答案:B31.建立一个数学模型与求解一道数学题目没有差别A.错误B.正确正确答案:A32.利用数据来估计模型中出现的参数值称为模型参数估计A.错误B.正确正确答案:B33.渡口模型涉及到先到后服务的排队问题A.错误B.正确正确答案:A34.数学建模没有唯一正确答案A.错误B.正确正确答案:B35.论文写作的目的在于表达你所做的事情A.错误B.正确正确答案:B36.交流中必须学会倾听A.错误B.正确正确答案:B37.数据的动态性又称为记忆性A.错误B.正确正确答案:B38.面向事件法又称时间增量法A.错误B.正确正确答案:A39.微元法的思想是考察研究对象的有关变量在一个很小的时间段内的变化情况A.错误B.正确正确答案:B40.国际上仅有一种单位体系A.错误B.正确正确答案:A二、多选题(共10 道试题,共20 分)1.数据作用于模型有以下形式____A.在建立模型的初始研究阶段,对数据的分析有助于我们寻求变量间的关系,形成初步的想法B.可以利用数据来估计模型中出现的参数值,称为模型参数估计C.利用数据进行模型检验正确答案:ABC2.创造性思维方法一般有____A.小组群体思维B.发散性思维方法C.从整体上把握问题的方法D.逐步分解法正确答案:ABC3.线性规划问题的特点是____A.每一个问题可用一组决策变量表示某一方案:这组决策变量的值就代表一个具体的方案B.存在一定的约束条件,这些约束条件可以用一组线性等式或线性不等式来表示C.都有一个要求达到的目标,它可以用决策变量的线性函数来表示,这个函数称为目标函数正确答案:ABC4.模拟随机变量常见方法有____A.利用理论分布B.基于对问题的实际、合理假设,选择适当的理论分布模拟随机变量C.基于实际数据的频率表作近似模拟正确答案:ABC5.对现实对象的认识主要来源有_________A.与问题相关的物理、化学、经济等方面的知识B.通过对数据和现象的分析对事物内在规律作出的猜想(模型假设)C.搜集一些对象的相关资料正确答案:AB6.分析检验一般有____A.量纲一致性检验B.参数的讨论C.假设合理性检验正确答案:ABC7.建立数学模型时可作几方面的假设____A.关于是否包含某些因素的假设B.关于条件相对强弱及各因素影响相对大小的假设C.关于变量间关系的假设D.关于模型适用范围的假设正确答案:ABCD8.实验误差有____A.随机误差B.系统误差C.过失误差正确答案:ABC9.建立微分方程模型一般的步骤是____A.把用语言叙述的情况化为文字方程B.给出问题所涉及的原理或物理定律C.列出微分方程,列出该微分方程的初始条件或其他条件D.求解微分方程,确定微分方程中的参数,最后求出问题的答案正确答案:ABCD10.使用模拟系统应达到的目标有()A.描述一个现有的系统B.探索一个假设的系统C.设计一个改进的系统正确答案:ABC。
第二次数学建模作业
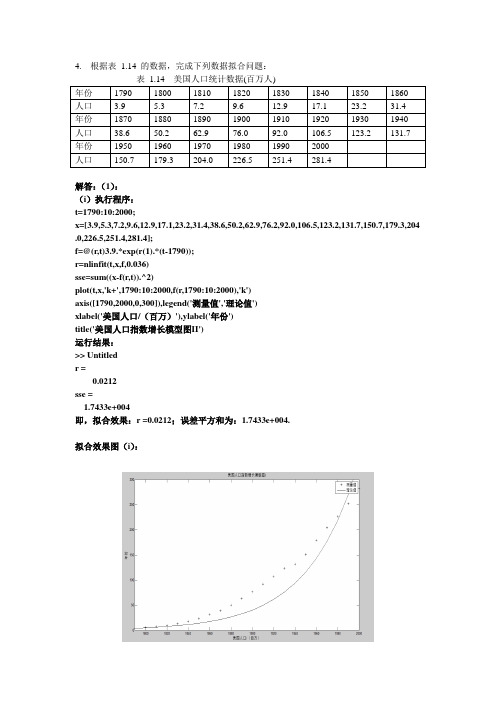
4. 根据表1.14 的数据,完成下列数据拟合问题:年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答:(1):(i)执行程序:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/(百万)'),ylabel('年份')title('美国人口指数增长模型图II')运行结果:>> Untitledr =0.0212sse =1.7433e+004即,拟合效果:r =0.0212;误差平方和为:1.7433e+004.拟合效果图(i):(ii)由表1.14我们知道,当t=1800时,有5)101(0≈+r x ,所以我们可以猜测,r=0.1,x =2.5.对待定参数0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下: >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道,拟合结果为:r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图(ii ):(iii)由表1.14我们知道,当t=1900时,有()76)-t 1900101(00≈+r x ,所以我们可以猜测,r=0.03,x =19, 0t =1800.对待定参数0t ,0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下:>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即,拟合效果:r =0,0x =7.9,0t =1742.5;误差平方和为:2.2657e+003我们由MATLAB9给出的警告信息,知道这个拟合存在病态条件,所以数据可能拟合的不太好。
数学建模第二次作业

《数学建模》第二次作业一、填空题:一、一个连通图能够一笔画出的充分必要条件是( ).二、如图是一个邮路,邮递员从邮局A 动身走遍所有长方形街路后再返回邮局.若每一个小长方形街路的边长横向均为1km ,纵向均为2km ,则他至少要走( )km..3、设某种物资有两个产地21,A A ,其产量别离为10、20,两个销地21,B B 的销量相等均为15。
若是从任意产地到任意销地的单位运价都相等为,a 则最优运输方案与运价具有 两个特点。
4、设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若人口增加率是常数r ,那麽人口增加问题的马尔萨斯模型应为 .五、设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若允许的最大人口数为m x ,人口增加率由sx r x r -=)(表示,则人口增加问题的逻辑斯蒂克模型为 .二、分析判断题:一、从下面不太明确的叙述中肯定要研究的问题,需要哪些数据资料(至少列举3个),要做些甚麽建模的具体的前期工作(至少列举3个) ,成立何种数学模型:一座高层办公楼有四部电梯,早晨上班时刻超级拥堵,该如何解决。
二、一条公路交通不太拥堵,以至人们养成“冲过”马路的适应,不肯意走临近的“斑马线”。
交管部门不允许任意横穿马路,为方便行人,预备在一些特殊地址增设“斑马线”,以便让行人能够穿越马路。
那末“选择设置斑马线的地址”这一问题应该考虑哪些因素?试至少列出3种。
3、地方公安部门想明白,当紧急事故发生时,人群从一个建筑物中撤离所需要的时刻,假设有足够的安全通道.若指挥者想尽可能多且快地将人群撤离,应制定甚麽样的疏散计划.请就那个计划指出至少三个相关因素,并利用数学符号表示。
4、作为经济模型的一部份,若产量的转变率与生产量和需求量之差成正比,且需求量中一部份是常数,另一部份与产量成正比,那麽相应的微分方程模型是甚麽?五、某种疾病每一年新发生1000例,患者中有一半昔时可治愈.若2000年末时有1200个病人,到2005年将会出现甚麽结果?有人说,无论多少年过去,患者人数只是趋向2000人,但不会达到2000人,试判断那个说法的正确性。
第二次数学建模

病人服药后病痛减轻时间与用药剂量、性别和血压组别关系模型摘要:为了掌握一种新止痛药的疗效,我们运用数学统计工具minitab 软件,通过对用药剂量,性别和血压组别之间的数据进行深层次地处理并加以讨论P (是否<0.05)及拟合的多元全相关系数R-Sq 和修正的多元相关系数R-Sq (调整)的值的相差程度,如果R-Sq 和R-Sq (调整)的差值越小,说明模型越好。
据此,我们假设出模型一:εββββ++++=3322110x x x Y然后通过分析讨论对模型一进行优化,最后得出女性病人服药后病痛减轻时间与用药剂量、性别和血压组别关系模型:2131326.032.91.568.31x x x x Y +-+=相对模型一较优,拟合的多元全相关系数R-Sq 和修正的多元相关系数R-Sq (调整)的值的相差程度为 1%。
男性病人服药后病痛减轻时间与用药剂量、性别和血压组别关系模型:213110427.0955.002.48.32x x x x Y ++-=相对模型一较优,拟合的多元全相关系数R-Sq 和修正的多元相关系数R-Sq (调整)的值的相差程度为 1.6%。
一、问题重述一个医药公司的新药研究部门为了掌握一种新止痛剂的疗效,设计了一个药物实验,给患有同种病痛的病人使用这种新止痛剂的一下4个剂量中的某一个:2g,5g,7g和10g,并记录每个病人病痛明显减轻的时间(以分钟计)。
为了了解新药的疗效与病人性别和血压有什么关系,实验过程中研究人员把病人按性别及血压的低、中、高三档平均分配来进行测试。
通过比较给个病人血压的历史数据,从低到高分成三组,分别记作0.25,0.50和0.75.实验结束后,公司的记录结果附录1-1表(性别以0表示,1表示男)。
现在为公司建立一个模型,根据病人用药的剂量、性别和血压组别,预⑴测出服药后病痛明显减轻的时间。
二、符号说明1、Y为病痛减轻时间量,单位(min);2、x表示用药剂量单位(g);13、x表示性别;24、x表示血压组别;35、P表示概率;6、R-Sq拟合的多元全相关系数;7、R表示此观测值含有大的标准化残差;8、S表是方差。
数学建模(2)第二次作业word版
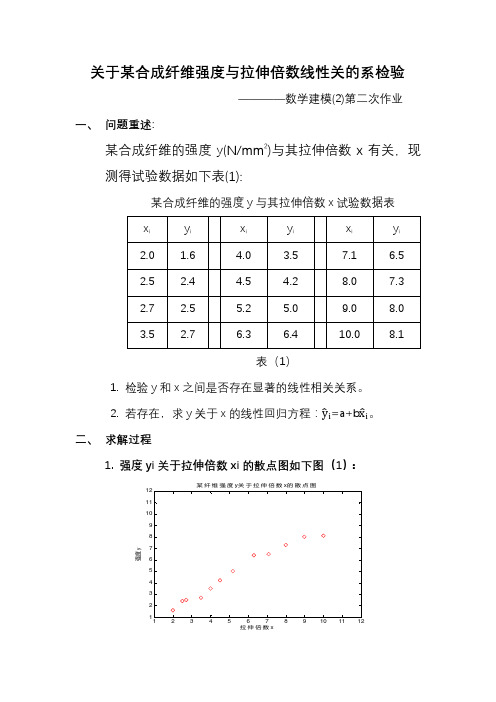
关于某合成纤维强度与拉伸倍数线性关的系检验————数学建模(2)第二次作业一、问题重述:某合成纤维的强度y(N/mm2)与其拉伸倍数x有关,现测得试验数据如下表(1):某合成纤维的强度y与其拉伸倍数x试验数据表表(1)1.检验y和x之间是否存在显著的线性相关关系。
2.若存在,求y关于x的线性回归方程:y i=a+b x i。
二、求解过程1.强度yi关于拉伸倍数xi的散点图如下图(1):图(1)2.样本相关系数计算 (1).计算公式r =nΣxy −ΣxΣynΣx 22nΣy 22(2)计算结果r =12∗382.17−3771.3612∗428.18−64.802∗ 12∗342.86−58.202=0.9859(3)结果分析r >0.8,说明该合成纤维强度y 与拉伸倍数x 成高度线性正相关关系。
2. 回归方程求解 (1).计算公式β1 =n ∑x i y i n i =1− ∑X i n i =1 ∑y i ni =1n x i2ni =1−∑x i n i =12某纤维强度y 关于拉伸倍数x 的散点图拉伸倍数x强度yβ 0=y −β1x (2).计算结果β 1= 12∗382.17−3771.3612∗428.18−64.802=0.8675β0=4.85−0.8675∗5.40=0.1655 (3).回归方程y i =0.1655+0.8675xi (4).回归前后图像对比图(2)回归系数β1=0.8675,表示拉伸倍数每增加一倍,该合成纤维强度增加0.08675。
三、 线性关系检验(1).提出假设123456789101112该纤维强度y 关于拉伸倍数x 的散点图及其线性回归方程拉伸倍数x强度yH0:β1=0线性关系不显著(2).计算检验统计量FF=SSR/1SSE/(n−2)= MSRMSE~F(1,n-2)F =58.89505/11.695902/(12−2)=347.2786(3).显著性水平α=0.05,根据分子自由度1和分母自由度12-2找出临界值Fα=4.965(4).F>Fα,拒绝H0,线性关系显著。
【奥鹏】2019秋福师《数学建模》在线作业二[3]答案
![【奥鹏】2019秋福师《数学建模》在线作业二[3]答案](https://img.taocdn.com/s3/m/3c97774e4b73f242326c5f55.png)
19秋福师《数学建模》在线作业二
试卷总分:100 得分:100
一、判断题(共40题,80分)
1、最小二乘法估计是常见的回归模型参数估计方法
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:B
2、我国对异常值没有颁布标准
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:A
3、测试分析将研究对象视为一个白箱系统
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:A
4、建模过程仅仅是建立数学表达式
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:A
5、对实际问题建模没有确定的模式
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:B
6、关联词联想法属于发散思维方法
A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]
正确的选择是:B
7、整个数学建模过程是又若干个有明显区别的阶段性工作组成A错误
B正确
[仔细阅读以上题目后,并运用所学知识完成作答]。
数学建模作业2

目录1问题 (1)2摘要 (1)3问题重述 (1)4问题分析 (2)5定义符号说明 (6)6流动的模型假设 (7)7模型的建立和求解 (7)8模型的分析 (9)10模型的评价和改进 (10)11参考文献 (12)中厚板轧机轧制压力数学模型研究一、问题由于目前国内多用两种炉型炼钢: 电炉炼钢和转炉炼钢, 致使相同钢种所含碳、锰、铜、硫、磷等元素不同量. 这表明, 研究适合于中厚板轧机的轧制压力模型势在必行. 针对生产实际状况, 拟用以下研究途径: 以生产钢种为对象, 在凸轮塑性计上测定流动应力, 建立流动应力模型; 采集轧钢现场数据, 建立应力状态系数模型, 从而得到整个轧制压力模型; 新轧制力模型离线和在线分析; 新轧制压力模型在线控制生产.二、摘要以现场的钢种为样本, 测定热轧条件下的流动应力, 建立流动应力模型. 采用现场实测轧制数据, 通过数值计算, 得到该轧机轧制压力模型. 以便于在投入计算机在线控制生产的时候,可以使生产的经济效益显著.关键词: 中厚板轧制; 轧制压力; 数学模型三、问题重述由于现代建设中,在不同环境中,需要不同种类的钢种,生产中产生不同种类钢种显得尤为重要,但是,各种生产模式之间的关系成为了投入计算机在线控制生产时的重要问题。
所以,以生产钢种为对象, 在凸轮塑性计上测定流动应力, 建立流动应力模型; 采集轧钢现场数据, 建立应力状态系数模型, 从而得到整个轧制压力模型; 新轧制力模型离线和在线分析; 新轧制压力模型在线控制生产.四、问题分析4.1 实验(1) 方法采用恒应变速率的凸轮塑性计, 用压缩端面上带凹槽并在凹槽里充满润滑剂的园柱形试件.经计算机采样测得.(2) 试验范围变形温度t= 850℃~1 150℃; 对数应变E= 0.05~0.69; 应变速率Ea= 5~80 s- 1 .(3) 试验料从轧制后的钢板上截取,经锻造、退火后截取试样,化学成分见表1.4. 2 数据分析在测定的钢种中, 其流动应力与变形温度的定性关系相一致. 图1 从中可看出, 在C相的流动应力与变形温度在半对数坐标中有较好的线性关系, 其直线斜率与钢种有关. 可以在C相, 变形温度对碳钢流动应力的影响项可用式( 1) , ( 2) 表示.Rt= ae At ( 1)式中, Rt 为随时间变化的流动应力; t 为时间; A 为钢的化学成份函数, A= f ( x%) ; x% 为钢的化学成份.由图2 可知, 流动应力与应变量随着变形温度、应变速率的变化, 存在着两种不同的应力应变曲线形状,即下降型和上升型. 在变形温度高和应变速率低时, 一般呈下降型, 反之呈上升型, 而且其曲线的形状与钢种有关, 即下式表示. 式中, b, B, C—取决于钢种的系数, B= f(x%) .研究表明, 应变速率对流动应力的影响不仅与钢中化学成份有关, 而且与变形温度有关.Rq= b( BE B - CE) ( 2)由图3 可知, 流动应力与应变速率在双对数坐标中呈线性关系, 其直线的斜率与钢种温度有关. 同时,A3 钢的流动应力高于B2F, 但当温度在1150℃时, 两种钢的流动应力差别并不显著. 经分析, 应变速率对流动应力的影响可用式( 3) 拟合. 即 ln(R/ R0 ) = m ln(Ea/E a 0) ( 3)式中, R0, E0 为基准流动应力和基准应变速率; m 为应变速率影响指数, 与钢的化学成份和温度有关.五、定义符号说明t:摄氏温度E:弹性模量Ea:抗拉压刚度R:中厚板轧制的流动应力T:开尔文温度Qp:应力状态系数P:轧制压力Bc:轧件入出口的平均板宽C:碳Mn:锰Si:硅Cu:铜六、流动模型的假设(1) 在流动应力模型中,不仅要考虑钢中碳锰含量的影响,也要考虑铜、硅等元素对流动应力的影响.(2) 变形温度对流动应力的影响最强烈,故在温度项中应包含碳、锰、铜、硅作为自变量来考虑.(3) 应变量对流动应力的影响项,不能简单地用幂函数表示, 而应用非线性函数.(4) 在线控制的数学模型结构要简单,且便于计算机实时控制计算.七、模型的建立和求解7.1流动应力模型对试验测定的9 个钢种的5 139 组R= f ( t, E, Ea,C, Mn, Si , Cu) 数据, 用7 种结构形式的流动应力模型做非线性回归. 其中日本新日铁提供的流动应力模型回归的方差为0. 981, 其余6 个模型的方差为0. 853~0. 860, 明显优于原模型.经分析, 用于中厚板轧制的流动应力模型为R= K T K E K Ea ( 4)其中, K T = a 1·exp( a 2/ T + a3C+ a4Mn+ a 5Si+ a6Cu ) ;K E= a10(E/0.4)(a11+ a12Mn+ a13Ea- a14T )-(a10 - 1) E/ 0.4; K Ea=(Ea/ 10) ( aT+ a8C+ a9T ) ; T = ( t+ 273 )/1 000 .从模型的反算可知, 温度在900℃时, 新旧模型误差高达10%, 但大于1 000℃时, 其流动应力差别减小( 图4) .7.2 建立应力状态系数模型7.2.1 实测轧制数据的整理收集整理钢种及其化学成份, 轧制出口板厚和温度, 各道次的轧制厚度和宽度, 辊径、轧制压力、应变率、应变速度等数据, 便于建立应力状态系数模型.7.2.2 回归分析应力状系数模型应力状态系数模型的结构可分为两类Qp = f (H / D, E) ( 5)Qp = f ( l/ hc, E) ( 6)为研究建立实际可行的应力状态系数模型, 分析中厚板轧机的实际状况. 即采用模型结构为:Qp = f (H / D, l/ hc) ( 7)以4200 轧制实测71 块钢板, 697 个轧制道次的工艺参数为例. 其中SS41, 11 块; Q235- A, 10 块; Q235- B, 15 块; 16Mn, 15 块SM50B- 1, 20 块.得应力状态系数模型:Qp = 3. 938 - 3. 031l/ hc + 0. 762H 0 / D + 1. 303( l/ hc) 2 - 11. 783( l/ hc) ( H0 / D) -3. 594(H 0/ D) 2, l/ hc ≤ 1Qp = 8. 468 - 2. 838l/ hc - 145. 996H 0/ D - 0. 899( l/ hc) 2 + 69. 075( l/ hc) (H 0/ D) +399. 290(H 0 / D) 2 , l/ hc > 1 ( 8) 式中, l 为轧辊和轧件接触孤长的水平投影; hc 为轧件入出口的平均板厚; H 0 为轧件初始入口厚度; D 为轧机工作辊直径.7.3 应力状态系数模型的确定为分析检验式( 8) 的实际应用性, 用离线分析的方法, 在广泛范围内返算结果表明: 式( 8) 能很好地反映轧制压力随厚度变化的规律, Qp 的预报值与实测推算结果是一致的.八、模型的分析8.1 在应力状态系数Qp 模型与金属塑性变形抗力R模型确定之后, 中厚板轧制压力模型也随之确定. 即P = 1. 15QpBclcR ( 9)式中, P 为轧制压力, Bc 为轧件入出口的平均板宽.8.2 以4200 轧机生产用钢为试验对象, 用实验室凸轮塑性计测定金属变形抗力所建立的模型全面考虑了影响变形抗力的各个影响因素, 适用于中厚板轧制.8.3 由此得到的轧制压力模型在4200 轧制计算机控制使用是成功的.8.4 用新轧制压力模型在线控制生产, 轧制过程稳定, 安全可靠, 轧制压力预报精度高于国内同期的模型,各道次轧制压力偏差小于100 吨的频数提高到98. 6% .8.5 新轧制压力模型投入在线控制生产, 提高了负公差的轧制率, 经济效益显著.九、模型的评价和改进优点:在流动应力模型中,不仅考虑了钢中碳、锰含量的影响,也考虑铜、硅、等元素对流动应力的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
09 理综一班 小组成员:李希骏 20090003019 郑晓晓 20090003007 郝运 20092802061 程冬 20092301167
1、 (1) 解: 对于 “两秒准则” , 前后车距离 D 与车速 v 成正比关系 D K 2 v , 其中 K 2 2
(秒) 。对于“一车长度准则” , 假设车身的平均长度是 5m,则前后车距 D 与车速 v 成 正比关系 D K1 v ,其中 K1 1.1185 (秒) 。 所以, “一车长度准则”与“两秒准则”不一致。
12 11.5 11 10.5 10 9.5 9 8.5 8 p(t)=p(0)-gt
市 场 价 格 p(t)
p(t)=p(0)-gt +ht15
20
25 时间t
30
35
40
45
50
由图形可以看出: (2.3.1)式表示价格随时间均匀下降,而(1)式多了一个时间 的二次项,显然(1)式表示的价格随时间的变化要平稳一些,并且到了一定的 时候(t 很大的时候) ,价格还会随时间增加(h>0) 。这显然更符合实际情况一 些。并且,在 t=0 附近(1)式和(2.3.1)式的导数相近,在最佳出售时机附近 的误差也比较微小。 (2)为建立数学模型,引入以下记号: t ~ 从现在开始计算的饲养生猪的天数,t≥0; C(t) ~农场在未来 t天内累计投入的资金(元); c ~ 农场每天投入的资金(元); w(t) ~ 生猪在第t天的体重(公斤); r ~ 生猪体重每天的增加值(公斤/天); p(t) ~ 在第t天的生猪出售的市场价格(元/公斤); g ,h ~ p(t)的参数; R(t) ~ 在t天之后出售生猪的收入(元); Q(t) ~ 在t天之后出售生猪比现在出售多赚的纯利润(元).; 以下为模型假设: (1)农场每天投入的资金 c 为常数,c=3.2 元; (2)现在生猪的体重为w(0)=90公斤,体重每天的增加值r为常数,r=1公斤/天; (3)现在生猪出售的市场价格为p(0)=12元/公斤,g=0.08,h=0.0002; 按照我们引入的记号和提出的模型假设,
比较一车长度准则、两秒准则、理论值和刹车距离实测数据 180 160 140 120
距 离 ( m)
一车长度准则 两秒准则 刹车距离理论值 刹车距离的最小值、平均值和最大值
100 80 60 40 20 0
0
5
10
15
20 25 车 速 v( m/s )
30
35
40
用最大的刹车距离除于车速,即得到最大刹车距离所需要的尾随时间,并 以尾随时间为依据, ,提出更加安全的准则,例如“3 秒准则” 、 “4 秒准则” 或者“t 秒准则” 。 “t 秒准则”是指后车司机根据车速,从前车经过某一标志开始计时,经过 t 秒的时间后到达同一个标志。 不同的车速对应着不同的“t 秒准则” ,通过计算得如下表: 0~10 10~35 35~60 60~75 车速 (mph) t(s) 1 2 3 4 现画出“t 秒准则”的图,绘图程序如下: v=(20:5:80).*0.44704; d2=[18,25,36,47,64,82,105,132,162,196,237,283,334 22,31,45,58,80,103,131,165,202,245,295,353,418 20,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2;k1=0.75;k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40; plot([0,10*0.44704],[0, 10*0.44704],'k',... vi,k1.*vi+k2.*vi.*vi,'k:',[v;v;v],d,'ok','MarkerSize',2) legend('t 秒准则','刹车距离理论值',... '刹车距离的最小值、平均值和最大值',2) hold on plot([10,35]*0.44704,2*[10,35]*0.44704,'k',... [35,60]*0.44704,3*[35,60]*0.44704,'k',... [60,75]*0.44704,4*[60,75]*0.44704,'k') title('t 秒准则,刹车距离的模型和数据') xlabel ('车速 v(m/s)'),ylabel ('距离(m)')hold off
(6)
20 10 0 -10 -20 -30 -40 -50 10.8
0
5
10
15
20
25
30
35
40
C(t)=ct
(1) (2) (3)
p(t)=p(0)-gt+ht 2
w(t)=w(0)+rt
所以在 t 天之后出售生猪的收入为
R(t)=p(t)w(t)=p(0)w(0)+[rp(0)-gw(0) ]t+[hw(0)-gr] t 2 +rht 3
于是在 t 天以后出售生猪比现在出售多赚的纯利润为
t秒 准 则 ,刹 车 距 离 的 模 型 和 数 据 180 160 140 120
距 离 ( m)
t秒 准 则 刹车距离理论值 刹车距离的最小值、平均值和最大值
100 80 60 40 20 0
0
5
10
15
20 车 速 v(m/s)
25
30
35
40
由 “t 秒准则” 的图可知, 当车速低于 33.5m/s, 即小于 120km/h 或 75mph 时, “t 秒准则”是足够安全的。 表 尾随时间 车速(mph) 车速(m/s) 最大刹车距离 (m) 尾随时间(s) 20 8.9408 13.411 1.5 30 13.411 23.774 1.7727 35 15.646 29.413 1.8799 40 17.882 37.795 2.1136 45 20.117 46.482 2.3106 50 22.352 56.693 2.5364 55 24.587 68.732 2.7955 60 26.822 81.686 3.0455 65 29.058 96.469 3.3199 70 31.293 113.39 3.6234 75 33.528 132.74 3.9591 80 35.763 154.23 4.3125 4、先画出原假设和新假设的市场价格关于时间的函数的图像 p=@(a,t)a(1)-a(2).*t+a(3).*t.^2; a0=[12,0.08,0]; a1=[12,0.08,0.0002]; x=0:0.0001:50; plot(x,[p(a0,x);p(a1,x)],'k') xlabel('时间 t'), ylabel('市场价格 p(t)') gtext('p(t)=p(0)-gt') gtext(' p(t)=p(0)-gt +ht^2')
下面用 fminbnd 函数计算(6)的最大值: h0=0.0002; Q=@(h,t) h.*t.^3+(90.*h-0.08).*t.^2+1.6.*t; Z=@(t)-Q(h0,t); [t0,z0]=fminbnd(Z,0,50) 运行结果为: t0 = 13.829 z0 = -10.798 即生猪出售时机为 13.829 天,多赚的纯利润为 Q=10.798 元; 然而,0.829 天是没有意义的,又 Q(13)= 10.761; Q(14)=10.797 故出售时机实际上为 14 天,多赚的纯利润为 10.797 元。 下面将函数 Q0 在不同区间的图形画出: Q0=@(t) 0.0002.*t.^3+(90.*0.0002-0.08).*t.^2+1.6.*t; subplot(2,1,1), fplot(Q0,[0,50],'k'), subplot(2,1,2) , fplot(Q0,[13.2,14.5],'k'),
按照“两秒准则” ,后车司机从前车经过某一标志开始,默数两秒到达同一 标志,这表明前后车距与车速成正比例关系.引入以下符号: D~前后车距(m); v~车速(m/s); K2~按照”两秒准则”,D 与 v 之间的比例系数(s); 于是”两秒准则”的数学模型为 D=K2*v 由于汽车刹车距离为 d=k1*v+k2*v2 则 d-D=v(k1-K2+k2*v) 所以当 v<(K2-k1)/k2 时有 d<D,即前后车距大于刹车距离的理论值,可认为足 够安全.当 v>(K2-k1)/k2 时有 d>D,即前后车距大于刹车距离的理论值,不够安全. 代入 k1=0.75,k2=0.082678, 以及 K2=2, 计算得到当车速超过 15.12m/s( 约合 54.43km/h)时”两秒准则”就不够安全了,也就是说,”两秒准则”只适用于车速较慢 的情况. 下面,用画图的方法来衡量“两秒准则”是否足够安全,即把刹车距离实测 数据、理论值和“两秒准则”都画在同一个图上,根据图指出“两秒准则”足够 安全的车速范围。 绘图程序如下: v=(20:5:80).*0.44704; d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 334 22, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 418 20,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2; K2=2; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1; vi=0:40; plot( [0,40],[0,K2*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2) title('比较两秒准则、理论值和刹车距离实测数据') legend('两秒准则','刹车距离理论值','刹车距离的最小值、平均值和最大值',2) xlabel('车速 v(m/s)'), ylabel('距离(m)') 运行结果如下:
