数模第二次作业
第二次数学建模作业
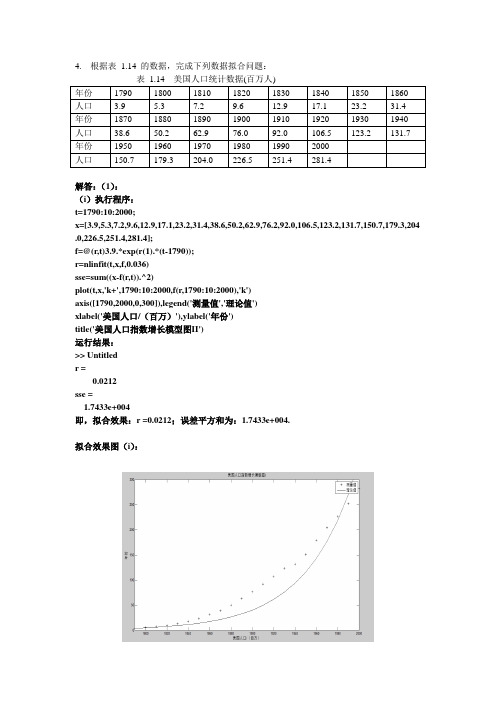
4. 根据表1.14 的数据，完成下列数据拟合问题：年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答：（1）：（i）执行程序：t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/（百万）'),ylabel('年份')title('美国人口指数增长模型图II')运行结果：>> Untitledr =0.0212sse =1.7433e+004即，拟合效果：r =0.0212；误差平方和为：1.7433e+004.拟合效果图（i）：(ii)由表1.14我们知道，当t=1800时，有5)101(0≈+r x ，所以我们可以猜测，r=0.1,x =2.5.对待定参数0x ，r 进行数据拟合同时进行绘图，其程序如下：t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/（百万）'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下： >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道，拟合结果为：r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图（ii ）：(iii)由表1.14我们知道，当t=1900时，有()76)-t 1900101(00≈+r x ，所以我们可以猜测，r=0.03,x =19, 0t =1800.对待定参数0t ,0x ，r 进行数据拟合同时进行绘图，其程序如下：t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/（百万）'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下：>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即，拟合效果：r =0，0x =7.9，0t =1742.5；误差平方和为：2.2657e+003我们由MATLAB9给出的警告信息，知道这个拟合存在病态条件，所以数据可能拟合的不太好。
数学建模作业题目
中原工学院2009年数学建模第二次模拟竞赛题A．飞机的登机顺序安排问题航空公司可以自由的安排等待登机的旅客的登机顺序，首先安排有特殊需要的乘客登机就座已经成为惯例. 按照常规有特殊需要的轮椅旅客首先登机，紧跟着是头等舱的乘客(他们坐在飞机的前部). 然后是安排经济舱和商务舱的乘客按行排队登机，从飞机后排的乘客依次往前安排登机。
从航空公司的角度来看,除了考虑到乘客的等待时间外,时间就是金钱,所以登机时间最好应该减小到最少. 只有飞机载客飞行，航空公司才能赚钱,而过长的登机时间将会限制飞机在一天内的飞行次数.发展大型飞机，诸如空客A380-800客机(载客800人) 这样的最小化登机（离机）时间的问题就更显得重要了。
（1）针对不同的小型(85-210座)、中型(210-330座)和大型(450-800座)客机，设计制订并比较不同乘客人数的登机或离机程序.（2）编写一份不超过两页纸的实施概要，你要阐明你们的研究结论。
阅读对象包括航空公司的业务主管、登机口的执法人员、空（地）勤有关人员.B．移动通讯基站建设问题某手机运营商准备在一个目前尚未覆盖的区域开展业务，计划投资5000万元来建设基站。
该区域由15个社区组成，有7个位置可以建设基站，每个基站只能覆盖有限个社区。
图1是该区域的示意图，每个社区简化为一个多边形，每个可以建设基站的位置已用黑点标出。
由于地理位置等各种条件的不同，每个位置建设基站的费用也不同，且覆盖范围也不同。
表1中列出了每个位置建设基站的费用以及能够覆盖的社区，表2列出了每个社区的人口数。
表1 每个位置建设基站的费用及所能覆盖的社区位置 1 2 3 4 5 6 7 费用（百万元）9.5 7 19 14 17.5 13 11覆盖社区1,2,4 2,3,5 4,7,8,10 5,6,8,9 8,9,12 7,10,11,12,15 12,13, 14,15表2 每个社区的人口数量社区 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 人口（千人） 2 4 13 6 9 4 7.5 12.5 10 11 6 14 9 3.5 6（1）在不超过5000万建设费用的情况下，在何处建设基站，能够覆盖尽可能多的人口；（2）考虑到基站出现故障维修的时候可能会出现所覆盖的社区信号中断等问题，为此对通讯资费进行了调整，规定，仅有一个基站信号覆盖的小区通讯资费按正常资费的68%收取，有两个或两个以上基站信号覆盖的小区的通讯资费按正常收取，针对于5000万元的预算，应该如何建设基站，才能够使得资费的收入达到最大。
数模第二次作业题目
一．食谱问题
某公司饲养实验用的动物以供出售。
已知这些动物的生长对饲料中的三种营养成分：蛋白质、矿物质、维生素特别敏感，每个动物每天至少需要蛋白质70g 、矿物质3g 、维生素10g ，该公司能买到5种不同的饲料，每种饲料1kg 所含营养成分如表1，每种饲料1kg 的成本如表2。
求既能满足动物生长需要，又使总成本最低的饲料配方并进行相关的灵敏性讨论。
表2：5种饲料单位重量(1kg)的成本
二．工资问题
现有一个木工，一个电工和一个油漆工，三人相互同意彼此装修他们自己的房子。
在装修之前，他们达成了如下协议：
（1）
每人总共工作10天（包括给自己家干活在内）； （2） 每人的日工资根据一般的市价在60----80元之间； （3） 每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案，如何计算出他们每人应得的工
现有一个木工，一个电工和一个油漆工，三人相互同意彼此装修他们自己的房子。
在装修之前，他们达成了如下协议：
（4）每人总共工作10天（包括给自己家干活在内）；
（5）每人的日工资根据一般的市价在60----80元之间；
（6）每人的日工资数应使得每人的总收入与总支出相等。
下表是他们协商后制定出的工作天数的分配方案，如何计算出他们每人应得的工
三．投资效益问题
一个投资公司有22亿资金可用来投资，现有6个项目可供选择，各项目所需资金和预计收益如下表：
问：选择哪几个项目投资，可使投资收益最大？
要求：1. 建立数学模型。
2. 提出一般的求解方法。
（穷举法不得分）。
数学建模第二次作业
《数学建模》第二次作业一、填空题：一、一个连通图能够一笔画出的充分必要条件是（ ）.二、如图是一个邮路，邮递员从邮局A 动身走遍所有长方形街路后再返回邮局.若每一个小长方形街路的边长横向均为1km ，纵向均为2km ，则他至少要走（ ）km..3、设某种物资有两个产地21,A A ，其产量别离为10、20，两个销地21,B B 的销量相等均为15。
若是从任意产地到任意销地的单位运价都相等为,a 则最优运输方案与运价具有 两个特点。
4、设开始时的人口数为0x ，时刻t 的人口数为)(t x ，若人口增加率是常数r ，那麽人口增加问题的马尔萨斯模型应为 .五、设开始时的人口数为0x ，时刻t 的人口数为)(t x ，若允许的最大人口数为m x ，人口增加率由sx r x r -=)(表示，则人口增加问题的逻辑斯蒂克模型为 .二、分析判断题：一、从下面不太明确的叙述中肯定要研究的问题，需要哪些数据资料（至少列举3个），要做些甚麽建模的具体的前期工作（至少列举3个） ，成立何种数学模型：一座高层办公楼有四部电梯，早晨上班时刻超级拥堵，该如何解决。
二、一条公路交通不太拥堵，以至人们养成“冲过”马路的适应，不肯意走临近的“斑马线”。
交管部门不允许任意横穿马路，为方便行人，预备在一些特殊地址增设“斑马线”，以便让行人能够穿越马路。
那末“选择设置斑马线的地址”这一问题应该考虑哪些因素？试至少列出3种。
3、地方公安部门想明白，当紧急事故发生时，人群从一个建筑物中撤离所需要的时刻，假设有足够的安全通道.若指挥者想尽可能多且快地将人群撤离，应制定甚麽样的疏散计划.请就那个计划指出至少三个相关因素，并利用数学符号表示。
4、作为经济模型的一部份，若产量的转变率与生产量和需求量之差成正比，且需求量中一部份是常数，另一部份与产量成正比，那麽相应的微分方程模型是甚麽？五、某种疾病每一年新发生1000例，患者中有一半昔时可治愈.若2000年末时有1200个病人，到2005年将会出现甚麽结果？有人说，无论多少年过去，患者人数只是趋向2000人，但不会达到2000人，试判断那个说法的正确性。
奥鹏福师21年秋季《数学建模》在线作业二_4.doc
1.数学建模的真实世界的背景是可以忽视的A.错误B.正确【参考答案】: A2.恰当的选择特征尺度可以减少参数的个数A.错误B.正确【参考答案】: B3.题面见图片A.错误B.正确【参考答案】: B4.现在公认的科学单位制是SI制A.错误B.正确【参考答案】: B5.蒙特卡罗模拟简称M-C模拟A.错误B.正确【参考答案】: B6.研究新产品销售模型是为了使厂家和商家对新产品的推销速度做到心中有数A.错误B.正确【参考答案】: B7.量纲分析是20世纪提出的在物理领域建立数学模型的一种方法A.错误B.正确【参考答案】: B8.利用数据来估计模型中出现的参数值称为模型参数估计A.错误B.正确【参考答案】: B9.数学建模中常遇到微分方程的建立问题A.错误B.正确【参考答案】: B10.整个数学建模过程是又若干个有明显区别的阶段性工作组成A.错误B.正确【参考答案】: B11.系统模拟是研究系统的重要方法A.错误B.正确【参考答案】: B12.数学建模以模仿为目标A.错误B.正确【参考答案】: A13.没有创新，人类就不会进步A.错误B.正确【参考答案】: B14.论文写作的目的在于表达你所做的事情A.错误B.正确【参考答案】: B15.建模中的数据需求常常是一些汇总数据A.错误B.正确【参考答案】: B16.我们研究染色体模型是为了预防遗传病A.错误B.正确【参考答案】: B17.在解决实际问题时经常对随机现象进行模拟A.错误B.正确【参考答案】: B18.对系统运动的研究不可以归结为对轨线的研究A.错误B.正确【参考答案】: A19.关联词联想法属于发散思维方法A.错误B.正确【参考答案】: B20.图示法是一种简单易行的方法A.错误B.正确【参考答案】: B21.捕食系统的方程是意大利学家Lanchester提出的A.错误B.正确【参考答案】: A22.问题三要素结构是初态，目标态和过程A.错误B.正确【参考答案】: B23.任何一个模型都会附加舍入误差A.错误B.正确【参考答案】: B24.现在世界的科技文献不到2年就增加1倍A.错误B.正确【参考答案】: A25.关键词不属于主题词A.错误B.正确【参考答案】: A26.利用无量纲方法可对模型进行简化A.错误B.正确【参考答案】: B27.赛程安排不属于逻辑分析法A.错误B.正确【参考答案】: A28.建模假设应是有依据的A.错误B.正确【参考答案】: B29.建模主题任务是整个工作的核心部分A.错误B.正确【参考答案】: B30.常用的建模方法有机理分析法和测试分析法A.错误B.正确【参考答案】: B31.量纲齐次原则指任一个有意义的方程必定是量纲一致的A.错误B.正确【参考答案】: B32.电-机类比是同一数学模型在科学上应用最为广泛的一种类比A.错误B.正确【参考答案】: B33.数据的需求是与建立模型的目标密切相关的A.错误B.正确【参考答案】: B34.随机误差不是由偶然因素引起的A.错误B.正确【参考答案】: A35.利用理论分布基于对问题的实际假设选择适当的理论分布可以对随机变量进行模拟A.错误B.正确【参考答案】: B36.数学建模的误差是不可避免的A.错误B.正确【参考答案】: B37.建立一个数学模型与求解一道数学题目没有差别A.错误B.正确【参考答案】: A38.数学建模没有唯一正确答案A.错误B.正确【参考答案】: B39.引言是整篇论文的引论部分A.错误B.正确【参考答案】: B40.数学建模第一步是明确问题A.错误B.正确【参考答案】: B41.采取面向事件法进行系统模拟的步骤是____A.写出实体（实体的特征），状态，活动B.确定系统的运转规则，画出说明事件和活动的流向图C.绘制轨迹表表格，产生随机数进行模拟D.写轨迹表【参考答案】: AB42.系统模拟的方式包括____A.计算机程序B.软件包或专用模拟语言C.列表手算【参考答案】: ABC43.数据作用于模型有以下形式____A.在建立模型的初始研究阶段，对数据的分析有助于我们寻求变量间的关系，形成初步的想法B.可以利用数据来估计模型中出现的参数值，称为模型参数估计C.利用数据进行模型检验【参考答案】: ABC44.分析检验一般有____A.量纲一致性检验B.参数的讨论C.假设合理性检验【参考答案】: ABC45.建立数学模型时可作几方面的假设____A.关于是否包含某些因素的假设B.关于条件相对强弱及各因素影响相对大小的假设C.关于变量间关系的假设D.关于模型适用范围的假设【参考答案】: ABCD46.任意分布随机数的模拟包括____A.离散型随机数的模拟B.连续型随机数的模拟C.正态随机数的模拟【参考答案】: ABC47.数学模型的误差原因有____A.来自建模假设的误差B.来自近似求解方法的误差C.来自计算工具的舍入误差D.来自数据测量的误差【参考答案】: ABCD48.正态随机数的模拟的方法有____A.反函数法B.舍选法模拟正态随机数C.坐标变换法D.利用中心极限定理【参考答案】: ABCD49.对模拟模型的分析包括____A.收集系统长期运转的统计值B.比较系统的备选装置C.研究参数变化对系统的影响D.研究改变假设对系统的影响E.求系统的最佳工作条件【参考答案】: ABCDE50.实验误差有____A.随机误差B.系统误差C.过失误差【参考答案】: ABC。
数学建模第二次作业
数学建模任意两个城市之间的最廉价路线参与人员信息：2012年 6 月 6 日一、问题提出某公司在六个城市C1、C2、C3、C4、C5、C6中都有分公司，从Ci 到Cj 的直达航班票价由下述矩阵的第i 行、第j 列元素给出（∞表示无直达航班），该公司想算出一张任意两个城市之间最廉价路线表，试做出这样的表来。
0 50 ∞ 40 25 1050 0 15 20 ∞ 25∞ 15 0 10 20 ∞40 20 10 0 10 2525 ∞ 20 10 0 5510 25 ∞ 25 55 0二 、问题分析若网络中的每条边都有一个数值(长度、成本、时间等)，则找出两节点(通常是源节点和阱节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。
最短路问题，我们通常归属为三类：单源最短路径问题、确定起点终点的最短路径问题、全局最短路径问题———求图中所有的最短路径。
题中要求算出一张任意城市间的最廉价路线表，属于全局最短路问题，并且使得该公司总经理能够与各个子公司之间自由往返。
（此两点为主要约束条件） Floyd 算法，具体原理如下：（1） 我们确定本题为全局最短路问题，并采用求距离矩阵的方法根据路线及票价表建立带权矩阵W ，并把带权邻接矩阵我w 作为距离矩阵的初始值，即(0)(0)()ij v v D d W ⨯==（2）求路径矩阵的方法在建立距离矩阵的同时可建立路径矩阵R ，()ij v v R r ⨯=，ij r 的含义是从i v 到j v 的最短路径要经过点号为ij r 的点。
（3）查找最短路径的方法若()1v ij r p =，则点1p 是点i 到j 的最短距离的中间点，然后用同样的方法再分头查找。
三、 模型假设：1.各城市间的飞机线路固定不变2.各城市间飞机线路的票价不改变3.忽略乘客除票价以外的各项开销费用4.不考虑雷雨云、低云、大风、雷暴、冰雹等主要天气因素对飞行的影响。
数学建模(2)第二次作业word版
关于某合成纤维强度与拉伸倍数线性关的系检验————数学建模(2)第二次作业一、问题重述:某合成纤维的强度y(N/mm2)与其拉伸倍数x有关，现测得试验数据如下表(1):某合成纤维的强度y与其拉伸倍数x试验数据表表（1）1.检验y和x之间是否存在显著的线性相关关系。
2.若存在，求y关于x的线性回归方程：y i=a+b x i。
二、求解过程1.强度yi关于拉伸倍数xi的散点图如下图（1）：图（1）2.样本相关系数计算 (1).计算公式r =nΣxy −ΣxΣynΣx 22nΣy 22(2)计算结果r =12∗382.17−3771.3612∗428.18−64.802∗ 12∗342.86−58.202=0.9859(3)结果分析r >0.8，说明该合成纤维强度y 与拉伸倍数x 成高度线性正相关关系。
2. 回归方程求解 (1).计算公式β1 =n ∑x i y i n i =1− ∑X i n i =1 ∑y i ni =1n x i2ni =1−∑x i n i =12某纤维强度y 关于拉伸倍数x 的散点图拉伸倍数x强度yβ 0=y −β1x (2).计算结果β 1= 12∗382.17−3771.3612∗428.18−64.802=0.8675β0=4.85−0.8675∗5.40=0.1655 (3).回归方程y i =0.1655+0.8675xi (4).回归前后图像对比图（2）回归系数β1=0.8675，表示拉伸倍数每增加一倍，该合成纤维强度增加0.08675。
三、 线性关系检验(1).提出假设123456789101112该纤维强度y 关于拉伸倍数x 的散点图及其线性回归方程拉伸倍数x强度yH0:β1=0线性关系不显著(2).计算检验统计量FF=SSR/1SSE/(n−2)= MSRMSE~F(1，n-2)F =58.89505/11.695902/(12−2)=347.2786(3).显著性水平α=0.05，根据分子自由度1和分母自由度12-2找出临界值Fα=4.965(4).F>Fα，拒绝H0，线性关系显著。
数模第二次作业
数模第二次作业姓名杜永志学号 ********学院理学院1．人员安排某公司的营业时间是上午8 点到22 点，以2 小时为一个时段，共7 个时段，各时段内所需的服务人员人数从早至晚分别为20，25，10，30，20，10，5，每个服务人员可在任一时段开始上班，但要连续工作8 小时，而工资相同，问应如何安排服务人员使公司所付工资总数最少，建立此问题的数学模型。
2、生产裸铜线和塑包线的工艺如下所示:1)拉丝机→裸铜线；2)拉丝机→塑包机→塑包线；3)联合机→塑包线某厂现有I型拉丝机和塑包机各一台，生产两种规格的裸铜线和相应达到两种规格的塑包线，没有联合机。
由于市场需求扩大和现有塑包机设备陈旧，计划新增II型拉丝机或联合机(每种设备最多1台)，或改造塑包机，每种设备选用方案及相关数据如下：已知市场对两种规格裸铜线的需求量分别为3000km和2000km，对两种规格塑包线的需求分别为10000km和8000km。
按照规定，新购及改进设备按每年5%提取折旧费，老设备不提；每台机器每年最多只能工作8000小时。
为了满足需求，确定使费用最小的设备选用方案和生产计划。
(只建立规划模型，不必求解)1解：设xi（i=1、2、3、4、5、6、7）为第i个时间段开始工作的员工数优化目标min x1+x2+x3+x4+x5+x6+x7约束条件（1）x1≥20（2）x1+x2≥25（3）x1+x2+x3≥10（4）x1+x2+x3+x4≥30（5）x2+x3+x4+x5≥20（6）x3+x4+x5+x6≥10（7）x4+x5+x6+x7≥5（8）xi为正整数利用lingo软件求解输入：min x1+x2+x3+x4+x5+x6+x7stx1>20x1+x2>25x1+x2+x3>10x1+x2+x3+x4>30x2+x3+x4+x5>20x3+x4+x5+x6>10x4+x5+x6+x7>5endgin 7输出：Global optimal solution found.Objective value: 40.00000Objective bound: 40.00000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations:Variable Value Reduced CostX1 20.00000 1.000000X2 10.00000 1.000000X3 5.000000 1.000000X4 5.000000 1.000000X5 0.000000 1.000000X6 0.000000 1.000000X7 0.000000 1.000000 即公司安排20个员工第1个时间段开始工作，10个员工第2个时间段开始工作，5个员工第3个时间段开始工作，5个员工第4个时间段开始工作，这样员工数最少，为40人，工资也最少。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数模第二次作业
姓名杜_永_志______________________
学号07114140 ___________________
学院理学院_________________________
1 •人员安排
某公司的营业时间是上午8点到22点，以2小时为一个时段，共7个时段，各时段内所需的服务人员人数从早至晚分别为20，25, 10，30，20，10，5, 每个服务人员可在任一时段开始上班，但要连续工作8小时，而工资相同，问
应如何安排服务人员使公司所付工资总数最少，建立此问题的数学模型。
2、生产裸铜线和塑包线的工艺如下所示：
1）拉丝机裸铜线；2）拉丝机塑包机塑包线；3）联合机塑包线
某厂现有I型拉丝机和塑包机各一台，生产两种规格的裸铜线和相应达到两种规格的塑包
线，没有联合机。
由于市场需求扩大和现有塑包机设备陈旧，计划新增II型拉丝机或联合
机（每种设备最多1台），或改造塑包机，每种设备选用方案及相关数据如下：
已知市场对两种规格裸铜线的需求量分别为3000km和2000km,对两种规格塑包线的需求分
别为10000km和8000km。
按照规定，新购及改进设备按每年5%提取折旧费，老设备不提; 每台机器每年最多只能工作8000小时。
为了满足需求，确定使费用最小的设备选用方案和
生产计划。
（只建立规划模型，不必求解）
1 解：设xi （i=1 、2、3、4、5、6、7）为第i 个时间段开始工作的员工数
利用lingo 输入：min x1+x2+x3+x4+x5+x6+x7 （1）x1 > 20
（2）x1+x2 > 25
（3）x1+x2+x3 > 10
（4）x1+x2+x3+x4 > 30 （5）x2+x3+x4+x5 > 20 （6）x3+x4+x5+x6 > 10 （7）x4+x5+x6+x7 > 5 （8）xi 为正整数
软件求解
优化目标
约束条件
min x1+x2+x3+x4+x5+x6+x7 st
x1>20
x1+x2>25
x1+x2+x3>10
x1+x2+x3+x4>30
x2+x3+x4+x5>20
x3+x4+x5+x6>10
x4+x5+x6+x7>5
end
gin 7
输出：
Global optimal solution found.
Objective value: Objective bound: Infeasibilities:
40.00000
40.00000 0.000000
Extended solver steps: Total solver iterations:
Variable Value
X1 20.00000 1.000000 X2 10.00000 1.000000 X3 5.000000 1.000000 X4 5.000000 1.000000 X5 0.000000 1.000000 X6 0.000000 1.000000 X7 0.000000 1.000000
20个员工第1个时间段开始工作Reduced Cost
10个员工第2个时间段开始工作
即公司安排
第3个时间段开始工作，5个员工第4个时间段开始工作，这样员工数最少，为，5个员工人，工资也
最少。
2解：设xi （i=1、2、3、4、5）表示第i 种方案，xi=1表示采用，xi=O 表示不采用。
tij （单 位为万小时 ）表示第 i 种方案机器生产第 j （j=1 、 2）规格产品的工作时间（注意只有 xi=1 是ti 才有意义）。
Z 为总费用（单位为万元）。
以一年时间为单位来研究问题。
目标函数 <1> 投资费 z1=20x2+10x4+50x5
<2> 运 行
z2=5x1(t11+t12)+7x2(t21+t22)+8x3(t31+t32)+8x4(t41+t42)+12x5(t51+t52)
<3> 固定费用 z3=3x1+5x2+8x3+10x4+14x4
<4> 废 品 损 失 费 z4=0.02*0.003* ( 10000t11+8000t12 ) *x1+0.02*0.003* ( 15000t21+14000t22
) *x2+0.03*0.005*
( 12000t31+10000t32 ) *x3+0.03*0.005*
( 16000t41+13000t42 ) *x4+0.03*0.005*
( 16000t51+12000t52 ) *x5
(5)折旧费 z5=0.05*20x2+0.05*10x4+0.05*50x5
则 z=z1+z2+z3+z4+z5
约束条件 ( 1 ) xi=0 或 1
( i=1 、 2、 3、 4、 5)
（2） x1=1 x3+x4=1
（3）时间限制（ti1+ti2）xi < 0.8
（ 4）产品需求量（裸铜线既要满足市场要求还要能满足塑包机生产用，另外还 要考
虑到是正品满足要求，即要剔除废品）
规格 1 裸铜线 0.98* (10000t11 + 15000t21*x2 ) > 3000+12000t31*x3+16000t41*x4
0.98* (8000t12+14000t22*x2 )> 2000+10000t32*x3+13000t42*x4 <3>规格 1 塑包线 0.97*(12000t31*x3+16000t41*x4+16000t51*x5) > 100000 <4>规格 2 塑包线 0.97*(10000t32*x3+13000t42*x4+12000t52*x5)
> 80000
将以上各式化简后输入 lingo 即可求得最优解。
<1> <2>规格 2 裸铜线
欢迎您的下载，
资料仅供参考!
致力为企业和个人提供合同协议，策划案计划书，学习资料等等
打造全网一站式需求。