高中数学选修4-1(人教版)练习：第二讲2.2圆内接四边形的性质与判定定理含解析

合集下载

人教A版数学选修4第二讲二圆内接四边形的性质与判定定理课时作业(含答案解析)

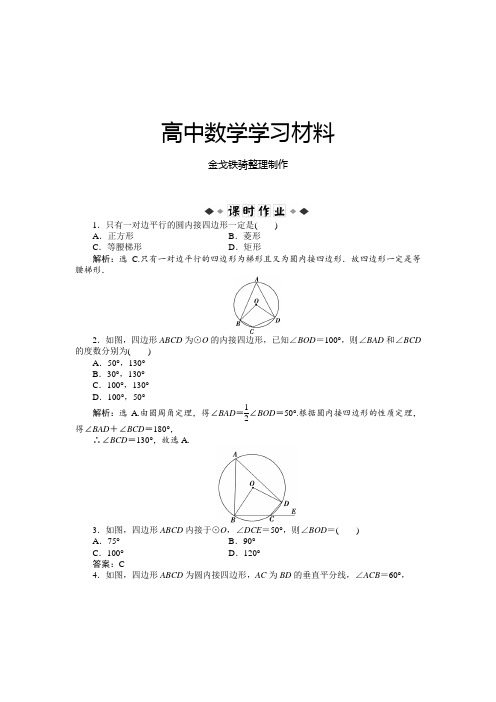
高中数学学习材料金戈铁骑整理制作1．只有一对边平行的圆内接四边形一定是( )A ．正方形B ．菱形C ．等腰梯形D ．矩形解析：选C.只有一对边平行的四边形为梯形且又为圆内接四边形．故四边形一定是等腰梯形．2．如图，四边形ABCD 为⊙O 的内接四边形，已知∠BOD ＝100°，则∠BAD 和∠BCD的度数分别为( )A ．50°，130°B ．30°，130°C ．100°，130°D ．100°，50°解析：选A.由圆周角定理，得∠BAD ＝12∠BOD ＝50°.根据圆内接四边形的性质定理，得∠BAD ＋∠BCD ＝180°，∴∠BCD ＝130°，故选A.3．如图，四边形ABCD 内接于⊙O ，∠DCE ＝50°，则∠BOD ＝( )A ．75°B ．90°C ．100°D ．120°答案：C4．如图，四边形ABCD 为圆内接四边形，AC 为BD 的垂直平分线，∠ACB ＝60°，AB ＝a ，则CD 等于( ) A.33a B.62a C.12a D.13a 解析：选A.∵AC 为BD 的垂直平分线，∴AB ＝AD ＝a ，AC ⊥BD ，∵∠ACB ＝60°，∴∠ADB ＝60°，∴AB ＝AD ＝BD ，∴∠ACD ＝∠ABD ＝60°，∴∠CDB ＝30°， ∴∠ADC ＝90°，∴CD ＝tan30°·AD ＝33a .5．如图，四边形ABCD 是⊙O 的内接四边形，且AB ＝CD ＝5，AC ＝7，BE ＝3，下列命题错误的是( )A ．△ABE ≌△DCEB ．∠BDA ＝45°C ．S 四边形ABCD ＝24.5D ．图中全等的三角形共有2对解析：选D.在△ABE 和△CDE 中，∠CAB ＝∠CDB ，∠AEB ＝∠DEC ，AB ＝CD ， ∴△ABE ≌△DCE ，故A 正确；据此，也可得AE ＝DE ，BE ＝CE ＝3，∴AE ＝DE ＝4.∵在△ABE 中，AE 2＋BE 2＝AB 2，∴AC ⊥BD .∵AE ＝DE ，∴∠BDA ＝45°，故B 正确；S 四边形ABCD ＝2S △ABE ＋S △BEC ＋S △ADE＝2×12×3×4＋12×32＋12×42＝24.5，故C 正确；在该图形中，有3对全等三角形，故D 错误．6．过点P (－1,0)，作⊙C ：(x －1)2＋(y －2)2＝1的两切线，设两切点为A 、B ，圆心为C ，则过A 、B 、C 的圆的方程为________．解析：∵P A ⊥AC ，PB ⊥BC ，∴P 、A 、B 、C 四点共圆，且PC 是其直径，故此圆的方程为x 2＋(y －1)2＝2，即为过A 、B 、C 的圆方程．答案：x 2＋(y －1)2＝2.7．如图，AB ＝10 cm ，BC ＝8 cm ，CD 平分∠ACB ，则AC ＝________，BD ＝________.解析：∠ACB ＝90°，∠ADB ＝90°.在Rt △ABC 中，AB ＝10，BC ＝8，∴AC ＝AB 2－BC 2＝6.又∵CD 平分∠ACB ，即∠ACD ＝∠BCD ，∴AD ＝BD ，∴BD ＝ AB 22＝5 2. 答案：6 5 28．正方形ABCD 的中心为O ，面积为50 cm 2，P 为正方形内一点，且∠OPB ＝45°，P A ∶PB ＝3∶4，则PB ＝________.解析：如图，连接OA ，OB ，则∠OAB ＝45°，∠AOB ＝90°，∴∠OAB ＝∠OPB ＝45°.∴A ，B ，O ，P 四点共圆．∴∠APB ＝∠AOB ＝90°，即△APB 为直角三角形．∴AP 2＋PB 2＝AB 2＝50. 又∵P A ∶PB ＝3∶4，∴2516PB 2＝50，即PB ＝4 2 (cm)．答案：4 2 cm9．已知圆内接四边形ABCD 的边长分别是AB ＝2，BC ＝6，CD ＝DA ＝4，求四边形ABCD 的面积．解：由于四点共圆，∴∠B ＋∠D ＝180°.∴cos ∠B ＝－cos ∠D .根据余弦定理，得AC 2＝22＋62－2×2×6cos ∠B ＝22＋62＋2×2×6cos ∠D ， AC 2＝42＋42－2×4×4cos ∠D ，∴cos ∠D ＝－17，sin ∠D ＝sin ∠B ＝4 37. ∴四边形ABCD 的面积＝12×AB ×BC ×sin ∠B ＋12×AD ×DC ×sin ∠D ＝8 3.10．如图，锐角三角形ABC 的内心为I ，过点A 作直线BI 的垂线，垂足为H ，点E 为内切圆I 与边CA 的切点．(1)求证：A ，I ，H ，E 四点共圆；(2)若∠C ＝50°，求∠IEH 的度数．解：(1)证明：由圆I 与边AC 相切于点E ，得IE ⊥AE ，结合IH ⊥AH ，得∠AEI ＝∠AHI ＝90°.所以，四点A ，I ，H ，E 共圆．(2)由(1)知四点A ，I ，H ，E 共圆，则∠IEH ＝∠HAI .在△HIA 中，∠HIA ＝∠ABI ＋∠BAI ＝12∠ABC ＋12∠BAC ＝12(∠ABC ＋∠BAC )＝12(180°－∠C )＝90°－12∠C . 结合IH ⊥AH ，得∠HAI ＝90°－∠HIA ＝12∠C ，所以∠IEH ＝12∠C . 由∠C ＝50°，得∠IEH ＝25°.11．如图，已知AD 是△ABC 的外角∠EAC 的平分线，交BC 的延长线于点D ，延长DA 交△ABC 的外接圆于点F ，连接FB 、FC .(1)求证：FB ＝FC ；(2)求证：FB 2＝F A ·FD ；(3)若AB 是△ABC 外接圆的直径，∠EAC ＝120°，BC ＝6 cm ，求AD 的长．解：(1)证明：∵AD 平分∠EAC ，∴∠EAD ＝∠DAC .∵四边形AFBC 内接于圆，∴∠DAC ＝∠FBC .∵∠EAD ＝∠F AB ＝∠FCB ，∴∠FBC ＝∠FCB .∴FB ＝FC .(2)证明：∵∠F AB ＝∠FCB ＝∠FBC ，∠AFB ＝∠BFD ，∴△FBA ∽△FDB .∴FB FD ＝F A FB，∴FB 2＝F A ·FD . (3)∵AB 是圆的直径，∴∠ACB ＝90°.∵∠EAC ＝120°，∴∠DAC ＝12∠EAC ＝60°，∠BAC ＝60°. ∠D ＝30°.∵BC ＝6，∴AC ＝2 3 (cm)．∴AD ＝2AC ＝4 3 (cm)．。

高中数学选修4-1(人教版)练习：第二讲2.2圆内接四边形的性质与判定定理

第二讲直线与圆的位置关系2.2 圆内接四边形的性质与判定定理A级基础巩固一、选择题1．圆内接平行四边形一定是( )A．正方形B．菱形C．等腰梯形D．矩形解析：由于圆内接四边形对角互补，平行四边形的对角相等，所以圆内接平行四边形的各角均为直角，故为矩形．答案：D2．已知AB，CD是⊙O的两条直径，则四边形ADBC一定是()A．矩形B．菱形C．正方形D．等腰梯形解析：AB，CD均为⊙O的直径，故四边形ADBC的四个角均为直角，且对角线AB＝CD，所以四边形ADBC为矩形．答案：A3．四边形ABCD内接于圆，∠A∶∠B∶∠C＝7∶6∶3，则∠D等于( )A．36°B．72°C．144°D．54°解析：由圆内接四边形的性质定理，∠A＋∠C＝180°.又由∠A∶∠C＝7∶3，设∠A＝7x，∠C＝3x，则10x＝180°，即x＝18°，所以∠B＝6x＝108°.故∠D＝180°－∠B＝72°.答案：B4.如图所示，四边形ABCD是⊙O的内接四边形，E为AB的延长线上一点，∠CBE＝40°，则∠AOC等于( )A．20°B．40°C．80°D．100°解析：因为四边形ABCD是圆内接四边形，且∠CBE＝40°，由圆内接四边形性质知∠D＝∠CBE＝40°，又由圆周角定理知∠AOC＝2∠D＝80°.答案：C5．如图所示，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝5 5°，则∠BCD的度数为( )A．35°B．45°C．55°D．75°解析：如图所示，连接AD，则△ABD是直角三角形，∠ADB＝90°，则∠DAB＝90°－∠ABD＝35°，根据同弧所对的圆周角相等，∠BCD ＝∠DAB ＝35°.答案：A 二、填空题6.如图所示，四边形ABCD 是圆O 的内接四边形，延长AB 与DC 相交于点P .若PB ＝1，PD ＝3，则BCAD的值为____．解析：因为四边形ABCD 是圆内接四边形，所以∠BCP ＝∠A .又∠P ＝∠P ，所以△BCP ∽△DAP . 所以BC AD ＝PB PD ＝13.答案：137．如图所示，⊙O 1与⊙O 2相交于A ，B 两点，AC 是⊙O 1的直径，延长CA ，CB ，分别交⊙O 2于D ，E ，则∠CDE ＝______．解析：连接AB，因为AC是⊙O1的直径，所以∠ABC＝90°.又因为∠ABC＝∠ADE，所以∠ADE＝90°，即∠CDE＝90°.答案：90°8．如图所示，点A，B，C，D在同一个圆上，AB，DC相交于点P，AD，BC相交于点Q，如果∠A＝50°，∠P＝30°，那么∠Q＝_ _______．解析：因为∠A＝50°，∠P＝30°，所以∠QDC＝∠A＋∠P＝80°.又∠QCD＝∠A＝50°，所以∠Q＝180°－80°－50°＝50°.答案：50°三、解答题9.如图所示，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB＝CE.(1)证明：∠D＝∠E；(2)设AD不是⊙O的直径，AD的中点为M，且MB＝MC，证明：△ADE为等边三角形．证明：(1)由题设知A，B，C，D四点共圆，所以∠D＝∠CBE.由已知得∠CBE＝∠E，故∠D＝∠E.(2)设BC的中点为N，连接MN，则由MB＝MC知MN⊥BC，故O在直线MN上．又AD不是⊙O的直径，M为AD的中点，故OM⊥AD，即MN⊥AD.所以AD∥BC，故∠A＝∠CBE.又∠CBE＝∠E，故∠A＝∠E.由(1)知，∠D＝∠E，所以△ADE为等边三角形．10.如图所示，CD为△ABC外接圆的切线，AB的延长线交直线C D于点D，E，F分别为弦AB与弦AC上的点，且BC·AC＝DC·AF，B，E，F，C四点共圆．(1)证明：CA是△ABC外接圆的直径；(2)若DB＝BE＝EA，求过B、E、F、C四点的圆的面积与△AB C外接圆面积的比值．(1)证明：因为CD为△ABC外接圆的切线，所以∠DCB＝∠A，由题设知BCFA ＝DC EA，所以△CDB∽△AEF，所以∠DBC＝∠EFA.因为B、E、F、C四点共圆，所以∠CFE＝∠DBC，所以∠EFA＝∠CFE＝90°，所以∠CBA＝90°，所以CA是△ABC外接圆的直径．(2)解：连接CE，因为∠CBE＝90°，所以过B、E、F、C四点的圆的直径为CE，因为DB＝BE，CE＝DC，又因为BC2＝DB·BA＝2DB2，所以CA2＝4DB2＋BC2＝6DB2，又因为DC2＝DB·DA＝3DB2，所以CE2＝3DB2.所以过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值为12.B级能力提升1.如图所示，四边形ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD∶∠ECD＝3∶2，那么∠BOD等于( )A．120°B．136°C．144°D．150°解析：因为∠BCD∶∠ECD＝3∶2，且∠BCD＋∠ECD＝180°，所以∠ECD＝72°.由圆内接四边形的性质得∠A＝∠ECD＝72°.又由圆周角定理知∠BOD＝2∠A＝2×72°＝144°.答案：C2．两圆相交于A，B，过A作两直线分别交两圆于C，D和E，F.若∠EAB＝∠DAB，则CD＝________．解析：因为四边形ABEC为圆内接四边形，所以∠2＝∠CEB.又因为∠1＝∠ECB，且∠1＝∠2，所以∠CEB＝∠ECB.所以BC＝BE.在△CBD与△EBF中，∠ECD＝∠BEF，∠D＝∠F，BC＝BE，所以△CBD≌△EBF，所以CD＝EF.答案：EF3.如图所示，A，B，C，D四点在同一圆上，AD的延长线与BC 的延长线交于E点，且EC＝ED.(1)证明：CD∥AB；(2)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G ，F四点共圆．证明：(1)因为EC＝ED，所以∠EDC＝∠ECD.因为A，B，C，D四点在同一圆上，所以∠EDC＝∠EBA.故∠ECD＝∠EBA.所以CD∥AB.(2)由(1)知，AE＝BE.因为EF＝EG，故∠EFD＝∠EGC，从而∠FED＝∠GEC.如图，连接AF，BG，则△EFA≌△EGB，故∠FAE＝∠GBE.又CD∥AB，∠EDC＝∠ECD，所以∠FAB＝∠GBA.所以∠AFG＋∠GBA＝180°.故A，B，G，F四点共圆．。

数学人教A版选修4-1学案课堂导学第二讲第二节圆内接四边形的性质与判定定理 Word版含解析

课堂导学
三点剖析
一、圆内接四边形的性质
【例】如图,圆内接四边形中与的延长线交于点与交于点,则图中相似三角形有对.()
图
解析：△∽△.
同理,△∽△.
△∽△.
△∽△.
答案
二、四点共圆应用举例
【例】如图为半圆的直径、为半圆上两点,∠°,求∠.
图
解：连结,
是直径∠°
∠∠°∠°∠
∠°∠°°°.
三、圆内接四边形的判定(四点共圆)
【例】如图,梯形是等腰梯形∥,求证、、、共圆.
图
证明:∵梯形是等腰梯形,
∴∠∠.
又∵∥,
∴∠∠°.
∴∠∠°.∴、、、共圆.
温馨提示
证明四点共圆通常证四边形的对角互补或它的一个外角等于它的内角的对角.
【例】求证:一个非矩形的平行四边形没有外接圆.
图
已知:如图不是矩形.
求证没有外接圆.
证明:假设有外接圆.
那么∠∠°.
又∵中,∠∠,
∴∠°.
∴是矩形.
这与题设相矛盾,假设不正确.
∴非矩形平行四边形没有外接圆.
各个击破
类题演练
如图,四边形内接于⊙,∠°,那么∠的度数为()
图
°°°°
解析:∠∠°,∠°∠°.
答案
温馨提示
当遇到圆内接四边形时,应考虑内接四边形的性质定理,它是计算或证明角相等或互补的常用依据之一.
类题演练
如图,△的外角平分线交外接圆于,求证.
图
证明:∵、、、共圆,。

高中数学人教a版选修4-1学案：第2讲 2 圆内接四边形的性质与判定定理含解析

二圆内接四边形的性质与判定定理1．了解圆内接四边形的概念．2．掌握圆内接四边形的性质、判定定理及其推论，并能解决有关问题．(重点、易混点)[基础·初探]教材整理1 圆内接四边形的性质定理阅读教材P27～P28定理2，完成下列问题．1．定理1：圆的内接四边形的对角互补．如图2-2-1，四边形ABCD内接于⊙O，则有：∠A＋∠C＝180°，∠B＋∠D＝180°.图2-2-12．定理2：圆内接四边形的外角等于它的内角的对角．图2-2-2如图2-2-2，∠CBE是圆内接四边形ABCD的一外角，则有：∠CBE＝∠D.四边形ABCD内接于圆O，延长AB到E，∠ADC＝32°，则∠CBE等于( ) A．32°B．58°C．122°D．148°【解析】根据圆内接四边形的外角等于它的内角的对角知，∠CBE＝32°. 【答案】 A教材整理2 圆内接四边形的判定定理及推论阅读教材P28～P29，完成下列问题．1．判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．2．推论：如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆．若AD，BE，CF为△ABC的三条高线，交于H，则图2-2-3中四点共圆的组数是( )图2-2-3A．3 B．4C．5 D．6【解析】其中B，D，H，F共圆；C，D，H，E共圆；A，E，H，F共圆；A，F，D，C共圆；B，C，E，F共圆；A，B，E，D共圆．【答案】 D[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：解惑：疑问2：解惑：疑问3：解惑：。

选修4-1第二讲直线与圆的位置关系圆内接四边形的性质与判定定理课件人教新课标1

(1)证明:B,D,H,E四点共圆; A (2)证明:CE平分∠DEF.
F E
H
B
D
C
【本节收获】
性质定理1 圆内接四边形的对角互补.
性质定理2 圆内接四边形的外角等于它的内角的对角. 圆内接四边形判定定理：
如果一个四边形的对角互补,那么它的四个顶点共圆.
推论：如果四边形的一个外角等于它的内角的对角，那么
返回
课后作业
1.AD,BE是△ABC的两条高，求证：∠CED=∠ABC.
A
C E
D
B
2.如图，已知四边形ABCD内接于圆，延长AB和DC相
交于E,EG平分∠E,且与BC,AD分别相交于F,G.
求证： ∠CFG=∠DGF. A
B
F
E
G
C D
返回
再见
A
BE
（2）
性质定理2 圆内接四边形的外角等于它的内角的对角.
1.【圆内接四边形的性质】
性质定理1 圆内接四边形的对角互补
性质定理2 圆内接四边形的外角等于它的内角的对角.
思考3
上述定理的逆命题是什么？它们成立吗？
应该怎样来证明呢？
性质定理1的逆命题：如果一个四边形的对角互补,那么它的四个顶点共圆.
它的四个顶点共圆.
思想方法
(1)圆内接四边形性质定理为几何论证中角的相等或互补提供了一个理论根据，因而也为论证角边关系提供了一种新的途径．
(2)在解有关圆内接四边形的几何问题时，既要注意性质定理的运用，也要注意判定定理的运用，又要注意两者的综合运用．(3)构造全等或类似三角形，以到达证明线段相等、角相等或线段成比例等目的．
∠B+∠E=180° ∵∠B+∠ADC=180°

人教A版选修4-1配套练习第二讲2.2圆内接四边形的性质与判定定理 Word版含解析

第二讲直线与圆的位置关系圆内接四边形的性质与判定定理级基础巩固一、选择题．圆内接平行四边形一定是( )．菱形．正方形．矩形．等腰梯形解析：由于圆内接四边形对角互补，平行四边形的对角相等，所以圆内接平行四边形的各角均为直角，故为矩形．答案：．已知，是⊙的两条直径，则四边形一定是( )．菱形．矩形．等腰梯形．正方形解析：，均为⊙的直径，故四边形的四个角均为直角，且对角线＝，所以四边形为矩形．答案：．四边形内接于圆，∠∶∠∶∠＝∶∶，则∠等于( )．°．°．°．°解析：由圆内接四边形的性质定理，∠＋∠＝°.又由∠∶∠＝∶，设∠＝，∠＝，则＝°，即＝°，所以∠＝＝°.故∠＝°－∠＝°.答案：.如图所示，四边形是⊙的内接四边形，为的延长线上一点，∠＝°，则∠等于( )．°．°．°．°解析：因为四边形是圆内接四边形，且∠＝°，由圆内接四边形性质知∠＝∠＝°，又由圆周角定理知∠＝∠＝°.答案：．如图所示，若是⊙的直径，是⊙的弦，∠＝°，则∠的度数为( )．°．°．°．°解析：如图所示，连接，则△是直角三角形，∠＝°，则∠＝°－∠＝°，根据同弧所对的圆周角相等，∠＝∠＝°.答案：二、填空题.如图所示，四边形是圆的内接四边形，延长与相交于点.若＝，。

人教版高中数学选修4-1《2.2 圆内接四边形的性质与定理》

圆的内接四边形的性质定理1的推导：
连接OA、OC
C D
α
1 B 2
3600
1 D 2
β
O A B
1 B D 360 0 180 0 2 A C 1800
2、圆的内接四边形的性质定理1：
文字语言：圆的内接四边形对角互补符号语言：若四边形ABCD内接于圆O，则有
A D
A D E O C B
O B C
圆内接四边形
圆内接五边形
思考：
1.任意三角形都有外接圆，那么任意正方形都有外接圆吗？为什么？
2.任意矩形都有外接圆吗？为什么？ 3.等腰梯形呢？ 4.任意四边形都有外接圆吗？
如下四边形都内接于圆
A
D
A
D
A
D
A D
O B C
O B C
B
O C
B
O C
这些四边形有什么共同特征？
这与“三角形的外角大于任一不相邻的内角”矛盾
故点D不可能在圆内
4、圆的内接四边形的判定定理：
文字语言：如果一个四边形对角互补，那么这个四边形的四个顶点共圆
符号语言：在四边形ABCD中，如果则有A C 1800 或（ B D 1800 ），那么A、B、C、 D四点共圆
图形语言：
FQ AC .
求证：A、B、P、Q四点共圆
C
P Q A F B
练习1、如图，AD、BE是 ABC 的两条高.
求证： CED ABC
C E D
A
B
练习2、求证：对角线互相垂直的四边形中，各边中点在同一个圆周上。
B F E A H D G C
练习3、如图四边形ABCD内接于圆，延长AB和

人教版数学高二选修4-1导学案二圆内接四边形的性质与判定定理

二圆内接四边形的性质与判定定理1.理解圆内接四边形的两条性质定理，能应用定理解决相关的几何问题.2.理解圆内接四边形判定定理及推论，能应用定理及推论解决相关的几何问题．判断下列各命题是否正确．(1)任意三角形都有一个外接圆，但可能不止一个；(2)矩形有唯一的外接圆；(3)菱形有外接圆；(4)正多边形有外接圆．答案(1)错误，任意三角形有唯一的外接圆；(2)正确，因为矩形对角线的交点到各顶点的距离相等；(3)错误，只有当菱形是正方形时才有外接圆；(4)正确，因为正多边形的中心到各顶点的距离相等．1．圆内接多边形(1)如果多边形的所有顶点都在一个圆上，那么这个多边形叫做圆内接多边形，这个圆叫做多边形的外接圆．(2)如果四边形的四个顶点都在同一个圆上，则称该四边形为圆内接四边形，这个圆叫做四边形的外接圆．2．圆内接四边形的性质定理(1)定理1：圆的内接四边形的对角互补．(2)定理2：圆内接四边形的外角等于它的内角的对角．3．圆内接四边形的判定定理(1)圆内接四边形的判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．(2)圆内接四边形的判定定理的推论：如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆.要点一用圆内接四边形的性质定理解决与线段长度有关的问题例1如图，在⊙O中，AC＝AB，E是弦BC延长线上的一点，AE交⊙O于点D.求证：AC2＝AD·AE.证明如图，连接DC，AB.∵AC＝AB，∴∠ACB＝∠B.又∵四边形ABCD内接于⊙O，∴∠EDC＝∠B，∴∠ACB＝∠EDC.∴∠ADC＝∠ACE.又∵∠EAC＝∠CAD，∴△ADC∽△ACE，∴ACAE＝ADAC，∴AC2＝AD·AE.规律方法要证明等积式，因比例式是等积式的一种特殊形式，故可转化为比例式．只需找到包含AC、AD、AE的两个三角形来证明．而要证三角形相似，可借助圆内接四边形的性质，得出对应的角相等．跟踪演练1如图，ABCD是⊙O的内接四边形，DP∥AC，交BA的延长线于P，求证：AD·DC＝P A·BC.证明如图，连接BD.∵DP∥AC，∴∠PDA＝∠DAC.∵∠DAC＝∠DBC，∴∠PDA＝∠DBC.∵四边形ABCD是圆内接四边形，∴∠DAP＝∠DCB.∴△P AD∽△DCB.得P A∶DC＝AD∶BC，即AD·DC＝P A·BC.要点二利用圆内接四边形的性质定理求角例2如图，已知：AB是⊙O的直径，AC、DE是⊙O的两弦，且DE⊥AB，延长AC、ED相交于F，求证：∠FCD＝∠ACE.证明连接AE.∵∠FCD是四边形ACDE的外角，∴∠FCD＝∠AED，又AB是⊙O的直径，且AB⊥DE，∴AD＝AE，∴∠AED＝∠ACE，∴∠FCD＝∠ACE.规律方法利用圆内接四边形的性质定理求角(1)观察图形，找出圆内接四边形的对角或外角与其内对角；(2)利用圆内接四边形的性质定理1或性质定理2求出所要求的角．(3)当题目中出现圆内接四边形时，首先利用性质定理，再结合其他条件进行推理证明．跟踪演练2如图所示，在圆内接四边形ABCD中，AC平分BD，且AC⊥BD.∠BAD＝72°，求四边形其余的各角．解∵四边形ABCD是圆内接四边形，∴∠BAD＋∠BCD＝180°.又∵∠BAD＝72°，∴∠BCD＝108°.又∵AC平分BD，并且AC⊥BD，∴AC是四边形ABCD外接圆的直径．∴∠ABC＝∠ADC＝90°.要点三利用圆内接四边形的判定定理证明四点共圆问题例3如图所示，在△ABC中，AD＝DB，DF⊥AB交AC于F，AE＝EC，EG⊥AC交AB于G.求证：(1)D、E、F、G四点共圆；(2)G、B、C、F四点共圆．证明(1)如图，连接GF，取GF的中点H.∵DF⊥AB，EG⊥AC，∴△DGF，△EGF都是直角三角形．又∵点H是GF的中点，∴点H到D、E、F、G的距离相等，∴点H是过D、E、F、G的外接圆的圆心，∴D、E、F、G四点共圆．(2)连接DE.由(1)知D、G、F、E四点共圆．由四点共圆的性质定理的推论，得∠ADE＝∠AFG.∵AD＝DB，AE＝EC，∴D是AB的中点，E是AC的中点，∴DE∥BC，∴∠ADE＝∠B，∴∠AFG＝∠B，∴G、B、C、F四点共圆．规律方法判断四点共圆的步骤：(1)观察几何图形，找到一定点、一对对角或一外角与其内对角；(2)判断四点与这一定点的关系；(3)判断四边形的一对对角的和是否为180°；(4)判断四边形一外角与其内对角是否相等；(5)下结论．跟踪演练3已知四边形ABCD为平行四边形，过点A和点B的圆与AD、BC 分别交于E、F，求证：C、D、E、F四点共圆．证明连接EF，因为四边形ABCD为平行四边形，所以∠B＋∠C＝180°.因为四边形ABFE内接于圆，所以∠B＋∠AEF＝180°.所以∠AEF＝∠C.所以C、D、E、F四点共圆．要点四综合运用圆内接四边形的性质定理与判定定理解决问题例4已知CF是△ABC的边AB上的高，FP⊥BC，FQ⊥AC.求证：A、B、P、Q四点共圆．证明连接PQ，在四边形QFPC中，因为PF⊥BC，FQ⊥AC，所以∠FQA＝∠FPC＝90°.所以Q、F、P、C四点共圆．所以∠QFC＝∠QPC.又因为CF⊥AB，所以∠QFC与∠QF A互余．而∠A与∠QF A也互余，所以∠A＝∠QFC.所以∠A＝∠QPC.所以A、B、P、Q四点共圆．规律方法判断四点共圆的常用方法有(1)如果一个四边形的一组对角互补，那么这个四边形的四个顶点共圆；(2)如果一个四边形的一个外角等于它的内对角，那么这个四边形的四个顶点共圆．跟踪演练4如图，A，B，C，D四点在同一圆上，AD的延长线与BC的延长线交于E点，且EC＝ED.(1)证明：CD∥AB；(2)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．证明(1)因为EC＝ED，所以∠EDC＝∠ECD.因为A，B，C，D四点在同一圆上，所以∠EDC＝∠EBA.故∠ECD＝∠EBA.所以CD∥AB.(2)由(1)知，AE＝BE.因为EF＝EG，故∠EFD＝∠EGC，从而∠FED＝∠GEC.连接AF，BG，则△EF A≌△EGB，故∠F AE＝∠GBE.又CD∥AB，所以∠F AB＝∠GBA.所以∠AFG＋∠GBA＝180°.故A，B，G，F四点共圆.1．圆内接平行四边形一定是()A．正方形B．菱形C．等腰梯形D．矩形答案 D解析由于圆内接四边形对角互补，平行四边形的对角相等，所以圆内接平行四边形的各角均为直角，故为矩形．2．若BE和CF是△ABC的边AC和AB边上的高，则________四点共圆．答案B、C、E、F解析由∠BEC＝∠BFC＝90°，知△BCE和△BCF共圆．3．试说明矩形的四个顶点在以对角线的交点为圆心的同一个圆上．证明如图，∵四边形ABCD为矩形，∴OA＝OC，OB＝OD，又AC＝DB，∴OA＝OC＝OB＝OD.则点A、B、C、D到点O的距离相等，∴A、B、C、D这四个点在以点O为圆心，OA为半径的同一个圆上．4．如图所示，AD是△ABC外角∠EAC的角平分线，AD与三角形的外接圆⊙O交于点D.求证：DB＝DC.证明∵AD是△ABC的外角∠EAC的平分线，∴∠EAD＝∠CAD，由题意知A，B，C，D四点共圆，∴∠EAD＝∠BCD，又∵∠CAD＝∠CBD.∴∠DBC＝∠DCB.∴DB＝DC.1.对圆内接四边形的理解(1)圆内接四边形是圆内接多边形的一种特殊情况，它们的关系可以用集合形式表示：{圆内接四边形}⊆{圆内接多边形}．(2)掌握一些常见的结论，例如，正多边形一定存在外接圆；三角形一定存在外接圆，并且三角形的外接圆的圆心(即外心)是三条边的垂直平分线的交点；圆内接梯形一定是等腰梯形等．2．判断四点共圆的基本方法(1)如果四个点与一定点的距离相等，那么这四个点共圆；(2)如果一个四边形的一组对角互补，那么这个四边形的四个顶点共圆；(3)如果一个四边形的一个外角等于它的内对角，那么这个四边形的四个顶点共圆；(4)如果两个三角形有公共边，公共边所对的角相等且在公共边的同侧，那么这两个三角形的四个顶点共圆．。

人教版选修4-12.2圆内接四边形的性质与判定定理课件

∴∠E＋∠1＝180°
A
∵ADFB是⊙O2的内接四边形，
∴∠1＝∠F
C
O1
1
∴∠E＋∠F＝180°
E
B
∴CE∥DF
D
O2
F
小结：
圆的内接四边形的性质定理:
圆的内接四边形的对角互补，并且任何一个外角都等于它的内角的对角。
问题2：如何判定一个四边形有外接圆？
1.圆内接四边形的性质定理1的逆命题是什么吗？性质定理：圆的内接四边形的对角互补.
A
A+C= 1 3600 =1800， 2
α
O
β
同理∠B＋∠D＝180°.
B
C
圆内接四边形性质定理：
定理1.圆的内接四边形的对角互补.
引申：如果延长BC到E，那么
∠DCE＋∠BCD ＝ 180°.
D
又 ∠A ＋∠BCD＝ 180°；
所以∠A＝∠DCE. A
因为∠A是与∠DCE相邻
O
的内角∠DCB的对角，我们把∠A叫做∠DCE的内对角。 B
分析：不在同一直线上的三点确定一个圆。
经过A、B、C、三点作⊙O，
D
如果能够由条件得到⊙O过点D，
那么就证明了命题.
A
讨论： ⊙O与点D有几种位置关系？
O
三种：（1）点D在圆⊙O外；
（2）点D在圆⊙O内；（3）点D在圆⊙O上.
B
C
如果我们否定了点D在圆⊙O外和点D在圆⊙O内；则点D在圆⊙O上成立；
圆内接四边形的判定定理的推论：
推论：如果四边形的一个外角等于它的内角
的对角，那么这个四边形的四个顶点共圆。
已知：在四边形ABCD中，A=DCE，

数学人教A版选修4-1课后训练：第二讲二圆内接四边形的

圆内接四边形的性质与判定定理练习1下列说法正确的有( )①圆的内接四边形的任何一个外角等于它的内角的对角；②圆内接四边形的对角相等；③圆内接四边形不能是梯形；④在圆的内部的四边形叫圆内接四边形．A．0个 B．1个 C．2个 D．3个2圆内接平行四边形的对角线( )A．互相垂直 B．互相垂直平分C．互相平分且相等 D．相等且平分每组对角3如图，四边形ABCD是O的内接四边形，E为AB的延长线上一点，∠CBE＝40°，则∠AOC等于( )A．20° B．40°C．80° D．100°4如图，四边形ABCD是O的内接四边形，AH⊥CD，如果∠HAD＝30°，那么∠B＝( )A．90° B．120°C．135° D．150°5如图，在O中，弦AB的长等于半径，∠DAE＝80°，则∠ACD＝( )A．30° B．45°C．50° D．60°6如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P，若13PBPD，则BCAD的值为______．7如图，两圆相交于A，B两点，过点A的直线交两圆于点C，D，过点B的直线交两圆于点E，F，连接CE，DF，若∠C＝95°，则∠D＝__________.8(能力拔高题)已知圆内接四边形ABCD的边长分别是AB＝2，BC＝6，CD＝DA＝4，则四边形ABCD的面积等于__________．9如图，四边形ABCD是圆的内接四边形，过点C作DB的平行线交AB的延长线于E点，求证：BE·AD＝BC·C D．10(探究题)如图，已知P为正方形ABCD的对角线BD上一点，通过P作正方形的边的垂线，垂足分别为点E，F，G，H.你能判断出点E，F，G，H是否在同一个圆上吗？试说明你的猜想．参考答案1 答案：B ①是圆内接四边形的性质定理2，则①正确；圆内接四边形的对角互补，但不一定相等，则②不正确；圆的内接四边形可以是梯形，则③不正确；顶点在同一个圆上的四边形叫圆内接四边形，则④不正确.2 答案：C 圆内接平行四边形必为矩形，故其对角线互相平分且相等.3 答案：C ∵四边形ABCD 是O 的内接四边形，且∠CBE ＝40°，由圆内接四边形的性质，知∠D ＝∠CBE ＝40°，又由圆周角定理知∠AOC ＝2∠D ＝80°.4 答案：B ∵AH ⊥CD ，∴∠AHD ＝90°.∵∠HAD ＝30°，∴∠D ＝90°－∠HAD ＝60°. 又四边形ABCD 内接于圆， ∴∠B ＝180°－∠D ＝120°.5答案：C ∵四边形ABCD 内接于圆O ， ∴∠DAE ＝∠BCD ＝80°. ∵弦AB 的长等于半径， ∴弦AB 所对圆心角为60°.∴∠ACB ＝12×60°＝30°. ∴∠ACD ＝∠BCD －∠ACB ＝80°－30°＝50°.6 答案：13由于∠PBC ＝∠PDA ，∠P ＝∠P ，则△PAD ∽△PCB ，故13PB BC PD AD ==. 7 答案：85°8 答案：由于四点共圆，∴∠B ＋∠D ＝180°. ∴cos B ＝－cos D .根据余弦定理，得AC 2＝AB 2＋BC 2－2AB ×BC ×cos B ，AC 2＝AD 2＋DC 2－2AD ×DC ×cos D ，∴有AC 2＝22＋62－2×2×6×cos B ＝22＋62＋2×2×6×cos D ， AC 2＝42＋42－2×4×4×cos D ，∴cos D ＝17-，sin D ＝sin B∴四边形ABCD 的面积＝0.5×AB ×BC ×sin B ＋0.5×AD ×DC ×sin D ＝9 答案：分析：转化为证明△ADC ∽△CBE .证明：如图，连接AC ，∵四边形ABCD 为圆内接四边形， ∴∠ADC ＝∠EBC . 又BD ∥EC ，∴∠CEB ＝∠DBA . ∵∠ACD ＝∠DBA ，∴∠CEB＝∠ACD. ∴△ADC∽△CBE.∴AD BCDC BE，即BE·AD＝BC·CD.10答案：分析：根据正方形的对称性，可以猜想，此四个点应当在以O为圆心的圆上，于是连接线段OE，OF，OG，OH，再设法证明这四条线段相等.解：猜想：E，F，G，H四个点在以O为圆心的圆上.证明如下：如图，连接线段OE，OF，OG，OH.在△OBE，△OBF，△OCG，△OAH中，OB＝OC＝OA.∵PEBF为正方形，∴BE＝BF＝CG＝AH，∠OBE＝∠OBF＝∠OCG＝∠OAH＝45°.∴△OBE≌△OBF≌△OCG≌△OAH.∴OE＝OF＝OG＝OH.由圆的定义，可知E，F，G，H四个点在以O为圆心的圆上.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。