立体图形的练习题
一年级立体图形练习题

一年级立体图形练习题一、选择题1. 下列哪个图形是长方体?A. 圆形B. 正方体C. 长方体D. 三角形2. 一个正方体有几个面?A. 4个B. 6个C. 8个D. 10个3. 圆柱体的侧面展开是什么形状?A. 圆形B. 三角形C. 长方形D. 正方形4. 一个球体有几个面?A. 1个B. 2个C. 3个D. 无数个5. 下列哪个图形不是立体图形?A. 长方体B. 正方体C. 圆柱体D. 长方形二、填空题6. 一个长方体有____个顶点。
7. 一个正方体的每个面都是____形。
8. 圆柱体的底面是____形。
9. 球体是一个____面体。
10. 当你从不同方向看一个正方体时,你看到的都是____形。
三、判断题11. 长方体的每个面都是长方形。
()12. 正方体的每个面都是正方形。
()13. 圆柱体有两个底面和一个侧面。
()14. 球体的每个方向看起来都是一样的。
()15. 长方体和正方体都有12条边。
()四、简答题16. 描述一下长方体的特征。
17. 描述一下正方体的特征。
18. 描述一下圆柱体的特征。
19. 描述一下球体的特征。
20. 为什么说球体是一个单面体?五、操作题21. 请画出一个长方体,并标注出它的长、宽、高。
22. 请画出一个正方体,并标注出它的边长。
23. 请画出一个圆柱体,并标注出它的底面半径和高。
24. 请画出一个球体,并描述它的特性。
25. 请用橡皮泥或纸制作一个正方体,并描述制作过程。
六、综合应用题26. 如果你有一个长方体的盒子,它的长是10厘米,宽是8厘米,高是5厘米,请计算它的体积。
27. 假设你有一个正方体的骰子,它的边长是2厘米,请计算它的表面积。
28. 如果你有一个圆柱形的杯子,它的底面直径是8厘米,高是10厘米,请计算它的容积。
29. 假设你有一个球形的气球,它的直径是20厘米,请计算它的表面积。
30. 请描述一下如何用积木搭建一个长方体的房子,并说明需要多少块积木。
立体图形竞赛练习题.doc

立体图形竞赛练习题一、选择题(每题5分,共30分)1.如图1是图2中( )的表面展开图.(A )甲正方体 (B )乙正方体 (C )丙正方体(D )甲正方体或丙正方体 解:从展开图可以看出,每个面上至少有一块阴影,从而排除丙;又每个面上没有相邻的阴影,从而排除乙;故选(A )图1 图22.一个立方组合体的三视图如图3,则该组合体共有多少个小正方体( )( )(A )7个或8个 (B )8个或9个 (C )9个或10个 (D )11个 解:从主视图知正面7个,从左视图、俯视图知第二排3个故选(C )图33.如图4所示的立方体,如果把它剪开,可以是图( )图4(A ) (B ) (C ) (D ) 解:选(D )4.一个长方形折叠后能围成一个三棱柱,这个三棱柱的底面一定是( )(A )三角形 (B )等边三角形 (C )等腰三角形 (D )直角三角形 解:选(A )5.一个画家有14个棱长为dm 1的正方体,他在地面上把它们摆成如图5所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )(A) 233dm (B) 224dm (C) 221dm (D) 242dm图5 图6 图7解::这个模型的主视图如图6,它的面积是26dm ,其它的三个侧面的视图和它一样,故侧面积是222446dm dm =⨯; 这个模型的俯视图如图7, 它的面积是2933dm dm dm =⨯.所以涂上颜色的总面积是22233924dm dm dm =+.故选(A).二、填空题(每题5分,共30分)6.如图8,是标有1,2,3,4,5,6六个数字的一个正方体的三种不同摆法。
问三个正方体朝左的一面的数字之和是______. 图8解:有三个正方体中的已知数字可判断数字1与4相对,2与6相对,3与5相对,故三个正方体朝左的一面的数字和为5+1+4=107. 如图9,是一个大正立方体,把它的每个面都划分为9个小正方形,这个大正方体中共有多少个正方体。
第三单元认识立体图形(同步练习)-2023-2024学年人教版数学一年级上册
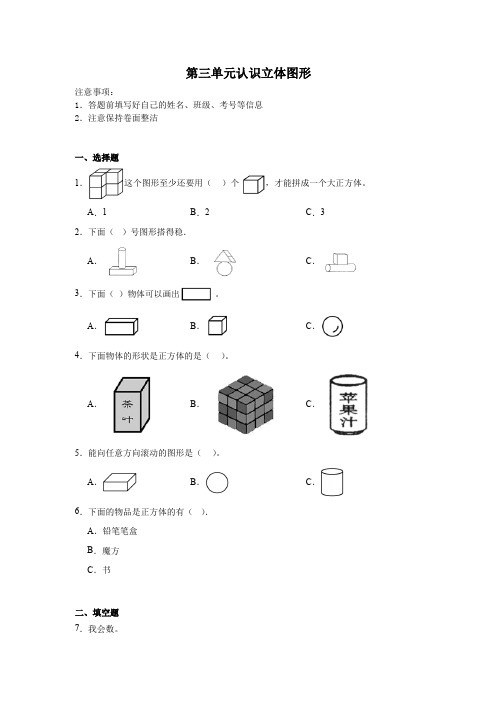
第三单元认识立体图形注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.注意保持卷面整洁一、选择题1.这个图形至少还要用()个,才能拼成一个大正方体。
A.1B.2C.32.下面()号图形搭得稳.A.B.C.3.下面()物体可以画出。
A.B.C.4.下面物体的形状是正方体的是()。
A.B.C.5.能向任意方向滚动的图形是()。
A.B.C.6.下面的物品是正方体的有().A.铅笔笔盒B.魔方C.书二、填空题7.我会数。
( )个,( )个,( )个,( )个。
8.在长方体的下面写“C”,在正方体的下面写“Z”.9.拼成的形状需要( )个。
10.长方体有( )个,正方体有( )个,圆柱有( )个,球有( )个;一共有( )个图形;( )最多,( )最少,( )和( )同样多。
11.数一数。
有( )个,有( )个,有( )个,有( )个。
12.长方体有( )个,圆柱有( )个,正方体有( )个,球有( )个。
三、判断题13.“七巧板”是由7块板组成,拼出来的图案变化万千。
( ) 14.数学课本是长方体,算术本是长方形。
( )15.我的数学课本是正方体。
( )16.用手摸一摸,圆柱上下两个面,它们的大小相同.( ) 17.长方体的六个面允许有两个面是一样大小的正方形。
( )四、解答题18.照样子把下列图形分成我们学过的图形.19.右面哪个图形是用左面两个图形拼起来的?圈一圈。
20.(1)左边有()个图形,右边有()个图形。
(2)把左边3个图形圈起来,从右边数第3个图形涂上你喜欢的颜色。
21.第一行摆第二行摆从第一行拿几个放到第二行,两行一样多?参考答案:1.B【分析】由题意可知,用8个小正方体能拼成一个大正方体,图中的图形用了6个小正方体,还差2个小正方体就能拼成一个大正方体了,据此解答即可。
【详解】这个图形至少还要用(2)个,才能拼成一个大正方体。
故答案为:B2.A【详解】略3.A【详解】略4.B【详解】略5.B【解析】略6.B【详解】略7. 4 2 1 4【分析】长方体是长长方方的有平平的面;正方体是正正方方的有平平的面;圆柱上下是圆且上下一样粗;球没有平面可以任意方向滚动的;根据立体图形的特征,先数一数,再填空即可。
立体图形的练习题

立体图形的练习题一、选择题(每题2分,共20分)1. 一个正方体的体积是27立方厘米,其棱长是:A. 3厘米B. 6厘米C. 9厘米D. 12厘米2. 一个长方体的长、宽、高分别是5厘米、4厘米和3厘米,其表面积是:A. 94平方厘米B. 114平方厘米C. 134平方厘米D. 154平方厘米3. 一个圆柱的底面半径为2厘米,高为5厘米,其体积是:A. 12π立方厘米B. 20π立方厘米C. 36π立方厘米D. 50π立方厘米4. 一个圆锥的底面半径为3厘米,高为4厘米,其体积是:A. 9π立方厘米B. 12π立方厘米C. 15π立方厘米D. 18π立方厘米5. 若一个球的体积是4/3π立方厘米,其半径是:A. 1厘米B. 2厘米C. 3厘米D. 4厘米二、填空题(每题2分,共20分)6. 一个长方体的长、宽、高分别是a厘米、b厘米和c厘米,其体积公式为:_________立方厘米。
7. 圆柱的体积公式为:底面积乘以_________。
8. 圆锥的体积公式为:1/3乘以底面积乘以_________。
9. 球的体积公式为:4/3π乘以_________的立方。
10. 若一个正方体的棱长为x厘米,其表面积公式为:_________平方厘米。
三、计算题(每题10分,共30分)11. 一个长方体的长为10厘米,宽为8厘米,高为6厘米,求其体积和表面积。
12. 一个圆柱的底面半径为4厘米,高为9厘米,求其体积和表面积。
13. 一个圆锥的底面半径为5厘米,高为12厘米,求其体积。
四、解答题(每题15分,共30分)14. 一个正方体的棱长为7厘米,求其对角线的长度。
15. 一个球的半径为8厘米,求其表面积和体积。
五、附加题(10分)16. 一个正四面体的棱长为a厘米,求其表面积和体积。
答案:1-5:A B C B A6-10:abc,高,高,半径,6x^211:体积=480立方厘米,表面积=596平方厘米12:体积=452π立方厘米,表面积=226π平方厘米13:体积=60π立方厘米14:对角线长度=7√3厘米15:表面积=502.4π平方厘米,体积=2048π立方厘米16:表面积=√3a^2平方厘米,体积=√2/12a^3立方厘米。
2024年数学七年级上册立体几何基础练习题(含答案)

2024年数学七年级上册立体几何基础练习题(含答案)试题部分一、选择题:1. 下列哪个图形是正方体?()A. 长方体B. 正六面体C. 圆柱体D. 球体2. 一个长方体的长、宽、高分别为2cm、3cm、4cm,它的对角线长度是多少cm?()A. 5cmB. 6cmC. 7cmD. 9cm3. 下列哪个图形的表面积最小?()A. 正方体B. 长方体C. 球体D. 圆柱体4. 一个正方体的体积是64立方厘米,它的棱长是多少厘米?()A. 2cmB. 4cmC. 6cmD. 8cm5. 下列哪个图形有6个面?()A. 三棱锥B. 四棱锥C. 圆锥D. 球体6. 一个圆柱的底面半径为3cm,高为5cm,它的侧面积是多少平方厘米?()A. 45πcm²B. 54πcm²C. 75πcm²D. 90πcm²7. 下列哪个图形的体积最大?()A. 长方体(长、宽、高分别为2cm、3cm、4cm)B. 正方体(棱长为3cm)C. 球体(半径为2cm)D. 圆柱体(底面半径为2cm,高为3cm)8. 一个圆锥的底面半径为4cm,高为3cm,它的体积是多少立方厘米?()A. 48πcm³B. 64πcm³C. 72πcm³D. 96πcm³9. 下列哪个图形可以展开成一个长方形?()A. 正方体B. 球体C. 圆锥D. 圆柱体10. 一个正方体的棱长为x,它的表面积是多少?()A. 6x²B. 8x²C. 12x²D. 24x²二、判断题:1. 正方体的六个面都是正方形。
()2. 圆柱体的底面和顶面都是圆形。
()3. 球体的表面积和体积相等。
()4. 长方体的对角线长度等于其长、宽、高的和。
()5. 圆锥的体积等于底面积乘以高。
()6. 正方体的体积是棱长的三次方。
()7. 两个相同体积的正方体,它们的表面积也相同。
初一立体图形练习题

初一立体图形练习题一、选择题(每题2分,共20分)1. 下列哪个选项不是立体图形?A. 立方体B. 圆柱C. 圆锥D. 长方形2. 一个长方体的长、宽、高分别为3cm、2cm和4cm,其体积是:A. 12cm³B. 24cm³C. 36cm³D. 48cm³3. 圆柱的底面半径为2cm,高为6cm,其体积是:A. 12πcm³B. 24πcm³C. 36πcm³D. 48πcm³4. 圆锥的底面半径为3cm,高为5cm,其体积是:A. 15πcm³B. 22.5πcm³C. 30πcm³D. 45πcm³5. 一个正方体的棱长为4cm,其表面积是:A. 64cm²B. 96cm²C. 128cm²D. 196cm²6. 一个球的半径为5cm,其体积是:A. 125πcm³B. 250πcm³C. 500πcm³D. 1000πcm³7. 一个棱锥的底面是正方形,边长为4cm,高为6cm,其体积是:A. 24cm³B. 32cm³C. 48cm³D. 64cm³8. 一个棱柱的底面是正六边形,边长为3cm,高为4cm,其体积是:A. 54cm³B. 72cm³C. 90cm³D. 108cm³9. 一个圆锥的底面直径为6cm,高为8cm,其体积是:A. 24πcm³B. 36πcm³C. 48πcm³D. 60πcm³10. 一个圆柱的底面直径为8cm,高为10cm,其体积是:A. 251.2πcm³B. 502.4πcm³C. 1004.8πcm³D.2009.6πcm³二、填空题(每题2分,共20分)11. 一个长方体的长、宽、高分别为a、b、c,其体积公式为________。
小学数学毕业考试立体图形真题练习

小学数学毕业考试立体图形真题练习一、选择题1.将一个正方体木块加工成一个最大的圆柱形木块,圆柱形木块上的底面直径是二、图形计算11.求表面积。
12.求下面组合图形的体积。
(单位:厘米,取3.14)=13.一个零件的形状如下图所示,求这个零件的体积。
三、解答题14.吴老师买了一套新房,客厅长6米,宽4米,高3米。
请同学们帮吴老师算一算装修所需要的部分材料。
(1)客厅准备用边长5分米的方砖铺地面,需要多少块?(2)准备粉刷客厅的四周墙壁和顶面,门窗、电视墙等10平方米不粉刷,实际粉刷的面积是多少平方米?15.神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱,将三名航天员运送至中国空间站。
神舟十三号乘组人员在空间站工作和生活六个月,创造了我国航天员在太空驻留天数的新纪录。
飞船主体由轨道舱、返回舱和推进舱构成。
轨道脑主体为圆柱形,集工作、吃饭和睡觉等诸多功能于一体,总长度为2.8米,直径约2.2米(如图)它的体积大约是多少?(得数保留一位小数)16.求瓶子的体积。
(单位:cm)17.一只底面半径为40厘米的圆柱形水桶内盛有80厘米深的水,将一个高8厘米的圆锥形铁块沉没水中,水没有溢出,水面上升1.5厘米,铁块的底面积是多少平方厘米?18.毕业啦!同学们用卡纸做了一顶“博士帽”(如图),帽子上面是边长为30厘米的正方形,下面是底面直径为20厘米、高为8厘米的无盖无底圆筒,做这顶帽子的上、下部分,分别用卡纸多少平方厘米?(连接处不计)18.一个圆锥形的沙堆,底面面积是28.26平方米,高是6米。
用这堆沙在20米宽的公路上铺2厘米厚的路面,能铺多少米?20.一块蛋糕如下图,在它的表面涂上奶油,需要涂多少平方厘米的奶油?这块蛋糕体积多大?21.一根长2米,横截面直径是20厘米的木头浮在水面上,它正好是一半露出水面。
(1)这根木头的体积是多少立方厘米?(2)这根木头与水接触的面积是多少平方厘米?22.如图是一个粮囤的示意图,它是由圆锥和圆柱两部分组成的。
立体图形练习题

一、基础概念题1. 请列举出三种常见的立体图形。
2. 立体图形的体积和表面积分别是什么?3. 立体图形的三视图分别是什么?4. 简述长方体、正方体、圆柱体、圆锥体的特征。
二、计算题1. 已知长方体的长、宽、高分别为10cm、6cm、4cm,求其体积和表面积。
2. 一个正方体的边长为8cm,求其体积和表面积。
3. 圆柱体的底面半径为5cm,高为10cm,求其体积和表面积。
4. 圆锥体的底面半径为3cm,高为4cm,求其体积和表面积。
三、应用题1. 一个长方体木块,长、宽、高分别为15cm、10cm、6cm,将其切割成最大的正方体,求正方体的边长。
2. 一个圆柱体水池,底面直径为10m,深为2m,求水池的容积。
3. 一个圆锥形帐篷,底面半径为6m,高为10m,求帐篷的占地面积。
4. 一块长方体铁块,长、宽、高分别为20cm、15cm、10cm,将其熔铸成一个球体,求球体的半径。
四、作图题1. 请画出长方体的三视图。
2. 请画出正方体的三视图。
3. 请画出圆柱体的三视图。
4. 请画出圆锥体的三视图。
五、判断题1. 立体图形的体积和表面积都是固定的。
()2. 长方体和正方体都是特殊的立方体。
()3. 圆柱体的底面一定是圆形。
()4. 圆锥体的侧面展开是一个扇形。
()六、选择题1. 下列哪个立体图形的体积公式是V = πr²h?A. 长方体B. 正方体C. 圆柱体D. 圆锥体2. 下列哪个立体图形的表面积公式是S = 2πrh + 2πr²?A. 长方体B. 正方体C. 圆柱体D. 圆锥体3. 一个正方体的边长为2cm,其体积为多少?A. 4cm³B. 8cm³C. 12cm³D. 16cm³4. 一个圆锥体的底面半径为3cm,高为4cm,其体积为多少?A. 12πcm³B. 36πcm³C. 48πcm³D. 144πcm³七、填空题1. 一个立方体的边长为5cm,其体积是______cm³,表面积是______cm²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体图形的复习练习题
一、判断:
(1)长方体和正方体都有六个面,十二个顶点,八条棱。
()(2)圆锥体的高有一条;圆柱体的高有两条。
()(3)圆柱的侧面展开是一个正方形,那么它的底面周长和高一定相等()(4)正方体的棱长总和是48厘米,它的每条棱长是8厘米。
()(5)圆柱体的体积等于圆锥体的3倍。
()(6)一个正方体的棱长是6厘米,它的表面积和体积相等。
()
2、求下列立体图形的表面积和体积;(只列式)
三、填空:
1、等底等高的圆柱与圆锥,已知圆锥的体积是24立方分米,则圆柱的体积是()
2、等底等高的圆柱与圆锥,它们的和是28立方米,则圆柱的体积是()
3、圆柱和圆锥的体积相等,底面积也相等,圆柱和圆锥的高的比是()
四、综合应用:
用一根长36分米的铁丝做一个长方体框架,使它的长:宽:高=2:3:4,在这个长方体框架外面糊一层包装纸,至少需要多少平方分米的纸?它的体积又是多少呢?
现有一个直径是4米,高6米的圆锥形沙堆,把它铺在一个宽10米,厚4cm的公路上,能铺多长?
五、巩固训练:
1、一个近似于圆锥的沙堆,测得底面直径是4米,高是1.5米。
每立方米沙约重1.6吨,这堆沙约重多少吨?(得数保留整吨数)
2、把一根长5米的圆柱形钢材截成三段后表面积比原来增加9.6平方分米,这根钢材原来的体积是多少?
3、一个直径是6分米,高是16分米的圆锥形容器,注满水后倒入底面直径是4分米的,高为20分米的圆柱形杯子中,问水面的高度是多少?
4、一个底面周长是6.28米,高6米的圆锥形沙堆,用这堆沙在5米宽的公路上铺4厘米厚的路面,能铺多少米?。
