电场强度叠加原理
场强叠加原理公式

场强叠加原理公式
电场场强叠加原理公式:
电场场强叠加原理公式表达的是两个电场的场强叠加,其数学表达式可以用下列公式表示:
E=E1+E2
其中E是两个电场在某一空间点的叠加电场强度,E1表示第一个电场在该点的电场强度,E2表示第二个电场在该点的电场强度。
磁场场强叠加原理公式:
磁场场强叠加原理公式也可以表示为两个磁场的场强叠加,其数学表达式可以用下列公式表示:
B=B1+B2
其中B是两个磁场在某一空间点的叠加磁场强度,B1表示第一个磁场在该点的磁场强度,B2表示第二个磁场在该点的磁场强度。
电磁波场强叠加原理公式:
电磁波场强叠加原理公式可以表示为两个电磁波的场强叠加,其数学表达式可以用下列公式表示:
E=E1+E2
B=B1+B2
其中E和B分别是两个电磁波在某一空间点的叠加电场和叠加磁场强度;E1和B1表示第一个电磁波在该点的电场和磁场强度;E2和B2表示第二个电磁波在该点的电场和磁场强度。
总之,场强叠加原理公式是电磁学中十分重要的公式,它可以帮助我们计算和预测电磁场的变化和传播规律。
在实际应用中,我们可以利用该原理来分析、设计和优化电磁设备和系统,从而提高其性能和可靠性。
电场强度叠加原理的应用

电场强度叠加原理的应用简介电场强度叠加原理是电学中重要的概念之一。
它描述了当存在多个电荷体系时,每个电荷体系所产生的电场强度可以通过向量叠加得到整个体系的电场强度。
这个原理在各个领域都有广泛的应用,下面将介绍几个具体的应用案例。
电荷体系叠加一个典型的应用场景是计算由多个点电荷组成的体系所产生的电场强度。
对于每个点电荷,可以计算出其在空间中的位置以及与其他点电荷之间的距离,进而得到其产生的电场强度。
然后,将所有点电荷的电场强度进行向量叠加,即可得到整个体系的电场强度。
电场强度叠加原理的应用不仅限于点电荷,对于分布式电荷体系,也可以采用类似的方法,将其划分为无数个微小的电荷元,然后通过叠加每个电荷元所产生的电场强度,最终得到整个体系的电场强度。
电场的叠加与屏蔽在现实生活中,我们常会遇到多个电场相互作用的情况。
根据电场强度叠加原理,我们可以将每个电场独立地分析,并将它们的电场强度进行向量叠加。
有时,多个电场之间会发生屏蔽现象。
屏蔽是指由于电场的相互作用,使得某些区域的电场强度明显减弱或者完全消失。
这种现象可以通过电场强度叠加原理来解释。
当两个电场方向相反,并且强度相当时,它们的向量叠加结果为零,即两个电场相互屏蔽。
电场的合成与分解电场强度叠加原理还可以用于电场的合成与分解。
在某些情况下,我们需要将一个复杂的电场分解为几个简单的电场分量进行分析。
这时,可以通过电场强度叠加原理将复杂电场拆分为几个已知的电场,从而更方便地进行计算。
同样地,根据电场强度叠加原理,我们也可以将多个已知电场进行叠加,得到一个复杂的电场。
这种合成的方法在电场分布复杂的情况下尤为有用,它能帮助我们准确地描述电场随空间分布的特性。
电场叠加的实际应用电场强度叠加原理在实际中有着广泛的应用。
以下是一些具体的应用案例:1.静电喷涂技术:将电荷赋予喷涂液体,通过叠加电场产生静电力,使液体粒子静电吸附在物体表面,实现均匀喷涂。
2.离子束注入技术:利用电场强度叠加原理,将离子束引入材料表面,改变材料结构和性质,应用于微电子器件的制造和材料表面改性。
电场叠加原理

电场叠加原理
电场叠加原理是电学中的一个重要概念,它描述了当存在多个电荷或电场时,它们对某一点的作用效果等于各个电荷或电场分别作用时的效果之和。
这一原理在电学领域有着广泛的应用,对于理解和分析电场的行为具有重要意义。
首先,我们来看一下电场叠加原理的基本表达式。
设有n个点电荷q1、q2、
q3...qn,分别位于r1、r2、r3...rn处,那么在某一点P处的电场强度E等于各个点电荷对该点产生的电场强度之和,即E=E1+E2+E3...+En。
其中Ei表示第i个点电荷对点P产生的电场强度。
这就是电场叠加原理的数学表达形式。
接下来,我们来看一些电场叠加原理的应用。
在实际问题中,往往会存在多个电荷或电场对某一点产生作用的情况,这时就可以利用电场叠加原理来求解问题。
比如,当有多个点电荷分布在空间中时,我们可以通过叠加原理来计算某一点的电场强度,从而分析该点的受力情况。
又如,在电容器中,如果存在多个电荷,我们也可以利用叠加原理来计算电容器的总电荷或总电场强度。
此外,电场叠加原理还可以帮助我们理解电场的叠加规律。
在空间中,如果存在多个电场,它们会相互叠加,形成一个合成的电场分布。
这时,我们可以利用叠加原理来分析合成电场的性质,从而更好地理解电场的行为。
总的来说,电场叠加原理是电学中一个非常重要的概念,它对于理解和分析电场问题具有重要意义。
通过对叠加原理的理解和运用,我们可以更好地解决电场问题,提高对电场行为的认识,为实际问题的分析和应用提供有力的支持。
因此,在学习电学知识的过程中,我们应该深入理解电场叠加原理,并灵活运用它来解决问题。
电场强度的叠加原理

电场强度的叠加原理
电场强度是描述电场强度大小的物理量,它的单位是高斯。
对于任意的一个点电荷,电场线的位置由该点电荷所受电场力的
方向和该点位置与该点电荷的电势差的方向共同决定。
我们知道,电场强度只与电荷有关,与电荷位置无关。
那么,电场强度的大小又由什么决定呢?这是因为:
(1)点电荷所在的位置与该点处电场强度的方向是互相垂
直的;
(2)一个点电荷所受电场力与它所在位置之间没有空间距离;
(3)一个点电荷所受电场力,是由它周围电场强度的叠加
而成的。
因此,在某一点附近,在一定范围内,其电场力之和等
于该点所受电场力。
我们可以这样来理解:如果我们在一个平面内画出一条平行线,那么在这条平行线上所有点的电场力之和等于它在这条平行
线上各点所受电场力之和。
很明显,电场强度可以看作是一种均
匀分布的力。
— 1 —
这样我们就把电场强度描述为场强叠加原理在整个空间中任意一点附近所产生的场强。
这样我们就得到了一个矢量,即:场强=电场强度矢量+电势差。
— 2 —。
用叠加原理求电场强度和电场力

用叠加原理求电场强度和电场力叠加原理是一种基本的电磁学原理,用于求解由多个电荷产生的电场的问题。
该原理基于电场是一个线性物理量的事实,即当有多个电荷同时存在时,它们各自产生的电场矢量可以简单地叠加在一起。
根据叠加原理,如果在空间中有多个电荷,那么在其中一点的电场强度是所有电荷在该点产生的电场强度的矢量和。
假设有n个电荷qi(i=1,2,...,n),其位置矢量为ri(i=1,2,...,n),则该点的电场强度E为:E=E1+E2+...+En其中,Ei是电荷qi在该点产生的电场强度。
根据库仑定律,电荷qi产生的电场强度Ei可以表示为:Ei = k * qi / ri^2 * ri/,ri其中,k为库仑常数,ri^2为电荷qi与该点的距离的平方, ri/,ri,为单位化的位置矢量。
由于电场是一个矢量量,所以叠加原理不仅适用于电场强度的叠加,也适用于电场力的叠加。
根据叠加原理,多个电荷对其中一点的电场力可以简单地叠加在一起。
假设有两个电荷q1和q2,在其中一点产生的电场力F可以表示为:F=F1+F2其中,F1为电荷q1对该点的电场力,F2为电荷q2对该点的电场力。
根据库仑定律,电荷q1对该点的电场力F1可以表示为:F1=k*q1*q/r^2*r/,r类似地,电荷q2对该点的电场力F2可以表示为:F2=k*q2*q/r^2*r/,r其中,r是该点与电荷q的距离,r/,r,是单位化的位置矢量。
通过以上的推导,我们可以使用叠加原理来求解由多个电荷产生的电场强度和电场力。
只需要计算每个电荷对其中一点的电场强度和电场力,然后将它们简单地叠加在一起即可。
需要注意的是,在实际应用中,叠加原理适用于处于远距离的电荷,也就是说两个电荷之间的距离要相对较大,以保证不会发生明显的相互作用影响。
如果两个电荷之间的距离较小,则必须考虑它们之间的相互作用效应,此时只使用叠加原理将得到不准确的结果。
除了叠加原理,还有一种更简单的方法来求解由多个电荷产生的电场强度和电场力,那就是使用超级叠加原理。
电场强度的叠加原理

电场强度的叠加原理嘿,咱们今天来聊聊电场强度的叠加原理。
你知道吗,这电场强度的叠加原理就像是一群小伙伴一起用力推一个大箱子。
每个人使的力大小和方向都不太一样,但是最后箱子受到的总的推力,就是把每个人的力加起来。
就说我之前有一次去看孩子们拔河比赛吧。
两队小朋友,每队都有十来个人,大家都紧紧拽着绳子,拼命往后拉。
这时候,每个人的力量就好像是电场中的一个电场强度。
有的小朋友力气大,有的小朋友力气小,有的往左边使劲儿,有的往右边使劲儿。
但是最后决定绳子往哪边移动的,可不是看某一个人的力量,而是把所有人的力量加在一块儿。
咱们回到电场强度的叠加原理上来。
假如在一个空间里,有两个点电荷,一个带正电,一个带负电。
那么正电荷会产生一个向外的电场,负电荷会产生一个向里的电场。
这两个电场在空间中的每一点相互叠加。
就好像拔河比赛中两队小朋友的力量在绳子上的每一点相互作用一样。
再比如说,在一个房间里,同时开着几台风扇。
每台风扇吹出的风都有自己的方向和速度,这就相当于每个点电荷产生的电场。
而房间里最终感受到的风的情况,就是把每台风扇吹出的风加在一起。
这就是电场强度的叠加原理在生活中的一个类比。
如果空间中有多个点电荷,那情况就更复杂啦。
但原理还是一样,就是把每个点电荷在某一点产生的电场强度按照矢量的加法法则加起来。
这就像是一群小朋友在操场上乱跑,每个人的速度和方向都不一样,要想知道在某个点上,这群小朋友总的运动趋势,就得把每个人的速度矢量加起来。
咱们来做个简单的计算。
假设有一个正电荷 Q1 在坐标原点,产生的电场强度为 E1;还有一个负电荷 Q2 在(a, 0) 点,产生的电场强度为 E2。
那么在点(x, y) 处的总电场强度 E 就等于 E1 + E2。
通过库仑定律和电场强度的公式,咱们就能算出具体的数值和方向。
在实际应用中,电场强度的叠加原理用处可大了。
比如说在电路设计中,电子在导线中流动会产生电场,多个电子的电场叠加起来,就会影响电流的分布和传输。
电场叠加原理

电场叠加原理
电场叠加原理是指在某个空间中,如果有多个电荷或电荷分布存在,那么在该空间中任一点的电场强度等于每个电荷或电荷分布所产生的电场强度的矢量和。
简言之,电场的叠加是线性的。
具体来说,如果在某一点P处有n个电荷qi(i=1,2,...,n),它们与该点的距离分别为ri,则该点处的电场强度可以表示为:
E=k*(q1/r1^2)*r1̂+k*(q2/r2^2)*r2̂+...+k*(qn/rn^2)*rn̂
其中,k为电场常数,r1̂、r2̂、...、rn̂分别为从电荷qi到点P的矢量方向,r1、r2、...、rn为它们的长度。
这一原理可以用于计算任意分布的电荷所产生的电场分布。
在实际应用中,我们可以将电荷分布离散化为若干小电荷,然后对每个小电荷的电场进行计算,并将结果进行叠加得到总电场分布。
需要注意的是,在考虑电场叠加时,应该同时考虑静电场和电磁场的叠加。
对于静电场,叠加原理适用于任意空间,而对于电磁场,则需要考虑相对论效应和场的传播特性等因素,可能会导致电磁场的非线性叠加。
总之,电场叠加原理是电学中的基本概念之一,它为我们计算和描述电场提供了重要的方法和工具。
在实际应用中,我们可以利用这一原理进行诸如电场分析、电场测量、电场模拟等方面的研究和设计。
第三讲 电场 电场强度 场强叠加原理 点电荷系的场强
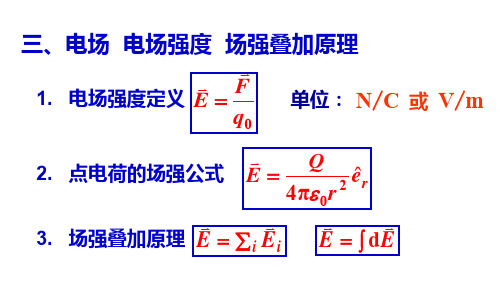
0q F E=1. 电场强度定义 单位: 2. 点电荷的场强公式 re r QE ˆπ420ε= 3. 场强叠加原理 N /C或 V /m三、电场 电场强度 场强叠加原理∑=i i E E ⎰=E Ed在电场中某一点的电场强度定义为 ,若该点没有试验电荷,那么该点的电场强度又如何,为什么?Q1.3.1答:不变。
0q F EQ1.3.2在地球表面上通常有一竖直方向的电场,电子在此电场中受到一个向上的力,电场强度的方向朝上还是朝下?答:朝下。
两个点电荷相距一定距离,已知在这两点电荷连线中点处电场强度为零。
你对这两个点电荷的电荷量和符号可作什么结论? 答:q 1 q 2 O q 1 q 2Q1.3.3在点电荷的电场强度公式中,若 r → 0,则电场强度的大小 E 将趋于无限大,对此,你有什么看法呢? 答:当 r → 0 时,公式没有意义。
r e rQ E ˆπ420ε= Q1.3.4Q1.3.5电力叠加原理和场强叠加原理是彼此独立没有联系的吗?答:不是。
∑==n i iF F 1 01q F n i i∑== 若带电体由 n 个点电荷组成, 由电力叠加原理 由场强定义 P ∑==n i i q F 10 ∑==n i i E 1q i q 1 0q F E=q 0r >> l 电偶极子 的方向由 -q 指向 +q +qO -qPr l 定义 电偶极矩 (electric moment ) lq p =p如图所示,一电偶极子的电偶极矩 ,P 点到电偶极子中心 O 的距离为 r ,r 与 l 的夹角为 q 。
在 r >> l 时,求 P 点的电场强度 在 方向的分量 E r 和垂直于 r方向上的分量 E q 。
-q +q l P r OQ1.3.6 l q p = OP r = q E22cos 21-+⎪⎭⎫ ⎝⎛-=q l r r 解: -q +q l -r +r +E -E P r O a - a + q 20π41++=r q E ε--++-=a a cos cos E E E r 20π41--=r q E ε; 1cos 1cos ≈≈-+a a ; ⎪⎭⎫ ⎝⎛+≈q cos 112r l r ⎪⎭⎫ ⎝⎛-≈⎪⎭⎫ ⎝⎛+=--q q cos 11cos 21222r l r l r r式中 又 q εεcos 2π411π430220r l q r r q E r ≈⎪⎪⎭⎫ ⎝⎛-=-+--+++=a a q sin sin E E E -q +q -r +r +E -E P r O l a - a + q q a a sin 2sin sin r l ≈≈-+⎪⎪⎭⎫ ⎝⎛+=-+22011sin 2π4r r r l q E q εq q εsin π430r l q ≈30cos 2π41r p q ε=30sin π41rp q ε=如图所示是一种电四极子,它由两个相同的电偶极子组成,这两个电偶极子在一直线上,但方向相反,它们的负电荷重合在一起。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
●◆☆★电场强度叠加原理
一般地说,电场是由电荷激发的。
为了显示电场的存在,并研究电场中各点(简称场点)的性质,我们通常取一个试探电荷放在各场点,以测定其所受的力。
如果在电场中某一个确定点上,先后放置一量值不同而同种的试探电荷、2、3、…,实验指出,试探电荷受力的方向相同、而大小不同,相应地为、2、3、…。
显然,在同一点P上,有
可见,在电场中的某一个确定点上,若试探电荷的量值改变,它所受的力的大小也改变,但它们两者之比这个矢量却是确定不变的,亦即其大小和力的方向是一定的。
换句话说,在电场中某一确定点上,尽管我们可以引入量值不同的试探电荷,然而,并不因之而变,它与试探电荷的量值无关。
对于电场中不同的点,一般来说,(包括其大小和的方向)也要随之而变,但各点分别有其确定的大小和方向。
由此可见,,因而它只与激发电场的场源电荷和电场中各点的位置有关。
于是,我们便可在电场中的每一点上,把所测出的作用于该处试探电荷上的力与之比,作为描述静电场性质的一个物理量,并称为电场强度,简称场强。
它是一个矢量,以符号(简称矢量)表示,即
从上述电场强度的定义式可知,电场中某点的电场强度(大小和方向)等于位于该点的单位正电荷所受的力。
也就是说,某一点的电场强度矢量,其大小等于单位正电荷在该点所受电场力的大小;其方向与正电荷在该点所受电场力的方向一致;与负电
荷在该点所受电场力的方向相反(如下图中的、等)。
场强的单位是(牛每库)或(伏每米)。
以后可以看到,这两种单位是等同的,在电工学中常常使用后者。
必须指出,只要有电荷存在就有电场存在,电场的存在与否是客观的,与是否引入试探电荷无关。
引入试探电荷只是为了检验电场的存在和讨论电场的性质而已。
正象人们使用天平可以称量出物体的质量,如果不用天平去称量物体,物体的质量仍然是客观存在的一样。
在点电荷、、…、共同激发的电场中某场点,放置一个试探电荷。
根据静电力的叠加原理,试探电荷
所受的力,等于各个点电荷、、…、单独存在时电场施于试探电荷的力、、…、之矢量和,即
今将上式两端除以,得
按场强定义,上式右端的各项分别是各点电荷(场源电荷)在同一点的场强,即:
左端代表这些点电荷同时存在时该点的总场强,即
于是,有
上式表明,电场中某点的总场强,等于各个点电荷单独存在时在该点的场强之矢量和。
这就是电场强度叠加原理。
它是电场的基本性质之一。
利用这个原理,我们可以计算任意点电荷系或带电体的场强(如图)。
所谓点电荷系,就是由若干个点电荷组成的集合。
例如,一个带电体,就可看作由许多点电荷构成的点电荷系。
