3电场强度叠加原理1
3电场强度叠加

电场强度的叠加考情分析一,知识导图二,重点知识透析电场强度是描述电场力的性质的物理量,是电场中最基本、最重要的概念之一,高中阶段的学习对整个电场部分起了辅垫作用,而在高考中也是考试的热点。
求解电场强度的基本方法有:1 定义法E=F/q,2 真空中点电荷场强公式法E=KQ/r2,3 匀强电场公式法E=U/d,4 若空间某位置的电场强度是由几个点电荷共同产生时,则该点的电场强度可认为等于每个点电荷单独存在时所激发的电场强度的矢量和。
矢量叠加法E=E1+E2+E3……等。
但对于某些电场强度计算,必须采用特殊的思想方法。
三典例分析一、叠加条件的理解如图所示,一导体球A带有正电荷,当只有它存在时,它在空间P点产生的电场强度的大小为E A,在A球球心与P点连线上有一带负电的点电荷B,当只有它存在时,它在空间P点产生的电场强度大小为E B,当A、B同时存在时,P点的场强大小应为A.E B B.E A+E B C.E A-E B D.以上说法都不对讲析因为导体球A不能视为点电荷,即引入电荷B后,导体球的电荷分布发生了变化,所以P点的电场强度无法确定,正确答案为D。
二利用叠加式E=E1+E2+…(矢量合成)求场强E2如图,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b 点处的场强为零,则d点处场强的大小为(k为静电力常量)( )A.k B.k C.k D.k[解析] 考查真空中点电荷的场强公式及场强的叠加.由题意,b点处的场强为零说明点电荷q和圆盘在b点产生的场强等大反向,即圆盘在距离为R的b点产生的场强为E Q=,故圆盘在距离为R的d 点产生的场强也为E Q=,点电荷q在d点产生的场强E q=,方向与圆盘在d点产生的场强方向相同,d点的合场强为二者之和,即E合=+=,B正确.3图中a、b是两个点电荷,它们的电量分别为Q1、Q2,MN是ab连线的中垂线,P是中垂线上,电荷连线上方的一点。
电场叠加原理

电场叠加原理
电场叠加原理是电学中的一个重要概念,它描述了当存在多个电荷或电场时,它们对某一点的作用效果等于各个电荷或电场分别作用时的效果之和。
这一原理在电学领域有着广泛的应用,对于理解和分析电场的行为具有重要意义。
首先,我们来看一下电场叠加原理的基本表达式。
设有n个点电荷q1、q2、
q3...qn,分别位于r1、r2、r3...rn处,那么在某一点P处的电场强度E等于各个点电荷对该点产生的电场强度之和,即E=E1+E2+E3...+En。
其中Ei表示第i个点电荷对点P产生的电场强度。
这就是电场叠加原理的数学表达形式。
接下来,我们来看一些电场叠加原理的应用。
在实际问题中,往往会存在多个电荷或电场对某一点产生作用的情况,这时就可以利用电场叠加原理来求解问题。
比如,当有多个点电荷分布在空间中时,我们可以通过叠加原理来计算某一点的电场强度,从而分析该点的受力情况。
又如,在电容器中,如果存在多个电荷,我们也可以利用叠加原理来计算电容器的总电荷或总电场强度。
此外,电场叠加原理还可以帮助我们理解电场的叠加规律。
在空间中,如果存在多个电场,它们会相互叠加,形成一个合成的电场分布。
这时,我们可以利用叠加原理来分析合成电场的性质,从而更好地理解电场的行为。
总的来说,电场叠加原理是电学中一个非常重要的概念,它对于理解和分析电场问题具有重要意义。
通过对叠加原理的理解和运用,我们可以更好地解决电场问题,提高对电场行为的认识,为实际问题的分析和应用提供有力的支持。
因此,在学习电学知识的过程中,我们应该深入理解电场叠加原理,并灵活运用它来解决问题。
电场强度叠加原理

电场强度叠加原理电场强度叠加原理是指在同一空间内,由多个电荷所产生的电场对某一点的电场强度之和等于各个电荷所产生的电场强度的矢量和。
这一原理在电场叠加的计算中起着非常重要的作用,下面我们将对电场强度叠加原理进行详细的介绍。
首先,我们来看一下电场强度的定义。
电场强度是指单位正电荷在电场中所受到的力,通常用E表示。
在电场中,如果有多个电荷分布在空间中,每个电荷都会产生一个电场,这些电场会相互影响并叠加在一起。
根据叠加原理,某一点的电场强度等于各个电荷产生的电场强度矢量和。
其次,我们来看一下电场强度叠加原理的具体计算方法。
假设空间中有n个电荷,分别为q1, q2, ..., qn,它们分别位于点P1, P2, ..., Pn,那么点P处的电场强度E等于各个电荷产生的电场强度矢量和,即:E = E1 + E2 + ... + En。
其中,E1, E2, ..., En分别为点P1, P2, ..., Pn处的电场强度。
这里需要注意的是,电场强度是矢量量,因此在进行叠加计算时需要考虑方向和大小。
接着,我们来看一下电场强度叠加原理的应用。
在实际问题中,我们经常会遇到多个电荷同时存在的情况,此时就需要利用电场强度叠加原理来计算电场强度。
例如,当我们需要计算某一点的电场强度时,首先需要找出该点受到影响的所有电荷,然后分别计算各个电荷产生的电场强度,最后将它们叠加在一起得到最终的电场强度。
最后,我们来总结一下电场强度叠加原理的特点。
电场强度叠加原理是电场叠加的基本原理,它适用于各种情况下的电场叠加计算。
在实际问题中,我们可以利用电场强度叠加原理来简化复杂的电场计算,从而更方便地分析和解决问题。
综上所述,电场强度叠加原理是电场叠加计算中的重要原理,它可以帮助我们更好地理解和计算电场的分布和作用。
在实际问题中,我们可以根据电场强度叠加原理来进行电场计算,从而更好地应用和理解电场的相关知识。
希望本文对您有所帮助,谢谢阅读!。
库仑定律 场强及叠加原理

3、一点电荷电场中某点受到的电场力很大,则该点的电场强度E:(C)
(A)一定很大(B)一定很小(C)可能大也可能小
4、两个电量均为+q的点电荷相距为2a,0为其连线的中点,则在其中垂线上场强具有极大值的点与0点的距离为:(C)
E=Ex= q/2π2ε0R2 ,场强方向为X轴的正方向
8、内半径为R1,外半径为R2的环形薄板均匀带电,电荷面密度为σ,求:中垂线上任一P点的场强及环心处0点的场强。
解:利用圆环在其轴线上任一点产生场强的结果
任取半径为r,宽为dr的圆环,其电量
dq=ds= 2rdr
在圆心处的场强为E0=0
a一定很大b一定很小c可能大也可能小4两个电量均为q的点电荷相距为2a0为其连线的中点则在其中垂线上场强具有极大值的点与2a5真空中面积为s间距均匀带等量异号电荷q和q忽略边缘效应则两板间相互作用力的大带等量同号电荷两者的距离远大于小球直径相互作用力为f
库仑定律、电场强度及场强叠加原理
1、电量Q相同的四个点电荷置于正方形的四个顶点上,0点为正方形中心,欲使每个顶点的电荷所受电场力为零,则应在0点放置一个电量q=-(1+22)Q/4的点电荷。
(A)F/2(B)F/4(C)3F/4(D)3F/8
7、如图所示,一均匀带电细棒弯成半径为R的半圆,已知 棒上的总电量为q,求半圆圆心0点的电场强度。
解:任取一段dl,其电量为dq=λdl=λRdθ
λ=q/πR,dE=dq/4πε0R2
dEx=dEcosθdEy=dEsinθ
由对称性可知Ey=0
Ex= dEx=q/2π2ε0R2
电场叠加原理

电场叠加原理
电场叠加原理是指在某个空间中,如果有多个电荷或电荷分布存在,那么在该空间中任一点的电场强度等于每个电荷或电荷分布所产生的电场强度的矢量和。
简言之,电场的叠加是线性的。
具体来说,如果在某一点P处有n个电荷qi(i=1,2,...,n),它们与该点的距离分别为ri,则该点处的电场强度可以表示为:
E=k*(q1/r1^2)*r1̂+k*(q2/r2^2)*r2̂+...+k*(qn/rn^2)*rn̂
其中,k为电场常数,r1̂、r2̂、...、rn̂分别为从电荷qi到点P的矢量方向,r1、r2、...、rn为它们的长度。
这一原理可以用于计算任意分布的电荷所产生的电场分布。
在实际应用中,我们可以将电荷分布离散化为若干小电荷,然后对每个小电荷的电场进行计算,并将结果进行叠加得到总电场分布。
需要注意的是,在考虑电场叠加时,应该同时考虑静电场和电磁场的叠加。
对于静电场,叠加原理适用于任意空间,而对于电磁场,则需要考虑相对论效应和场的传播特性等因素,可能会导致电磁场的非线性叠加。
总之,电场叠加原理是电学中的基本概念之一,它为我们计算和描述电场提供了重要的方法和工具。
在实际应用中,我们可以利用这一原理进行诸如电场分析、电场测量、电场模拟等方面的研究和设计。
第三讲 电场 电场强度 场强叠加原理 点电荷系的场强
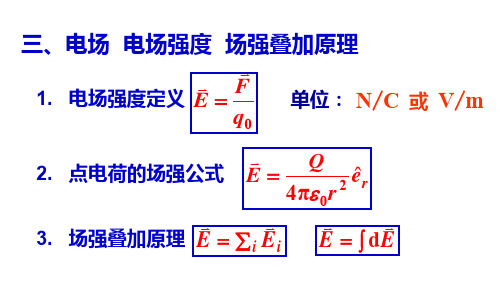
0q F E=1. 电场强度定义 单位: 2. 点电荷的场强公式 re r QE ˆπ420ε= 3. 场强叠加原理 N /C或 V /m三、电场 电场强度 场强叠加原理∑=i i E E ⎰=E Ed在电场中某一点的电场强度定义为 ,若该点没有试验电荷,那么该点的电场强度又如何,为什么?Q1.3.1答:不变。
0q F EQ1.3.2在地球表面上通常有一竖直方向的电场,电子在此电场中受到一个向上的力,电场强度的方向朝上还是朝下?答:朝下。
两个点电荷相距一定距离,已知在这两点电荷连线中点处电场强度为零。
你对这两个点电荷的电荷量和符号可作什么结论? 答:q 1 q 2 O q 1 q 2Q1.3.3在点电荷的电场强度公式中,若 r → 0,则电场强度的大小 E 将趋于无限大,对此,你有什么看法呢? 答:当 r → 0 时,公式没有意义。
r e rQ E ˆπ420ε= Q1.3.4Q1.3.5电力叠加原理和场强叠加原理是彼此独立没有联系的吗?答:不是。
∑==n i iF F 1 01q F n i i∑== 若带电体由 n 个点电荷组成, 由电力叠加原理 由场强定义 P ∑==n i i q F 10 ∑==n i i E 1q i q 1 0q F E=q 0r >> l 电偶极子 的方向由 -q 指向 +q +qO -qPr l 定义 电偶极矩 (electric moment ) lq p =p如图所示,一电偶极子的电偶极矩 ,P 点到电偶极子中心 O 的距离为 r ,r 与 l 的夹角为 q 。
在 r >> l 时,求 P 点的电场强度 在 方向的分量 E r 和垂直于 r方向上的分量 E q 。
-q +q l P r OQ1.3.6 l q p = OP r = q E22cos 21-+⎪⎭⎫ ⎝⎛-=q l r r 解: -q +q l -r +r +E -E P r O a - a + q 20π41++=r q E ε--++-=a a cos cos E E E r 20π41--=r q E ε; 1cos 1cos ≈≈-+a a ; ⎪⎭⎫ ⎝⎛+≈q cos 112r l r ⎪⎭⎫ ⎝⎛-≈⎪⎭⎫ ⎝⎛+=--q q cos 11cos 21222r l r l r r式中 又 q εεcos 2π411π430220r l q r r q E r ≈⎪⎪⎭⎫ ⎝⎛-=-+--+++=a a q sin sin E E E -q +q -r +r +E -E P r O l a - a + q q a a sin 2sin sin r l ≈≈-+⎪⎪⎭⎫ ⎝⎛+=-+22011sin 2π4r r r l q E q εq q εsin π430r l q ≈30cos 2π41r p q ε=30sin π41rp q ε=如图所示是一种电四极子,它由两个相同的电偶极子组成,这两个电偶极子在一直线上,但方向相反,它们的负电荷重合在一起。
微专题43 电场强度的叠加-2025版高中物理微专题

微专题43电场强度的叠加【核心考点提示】求合场强的四种特殊方法电场的叠加原理:如果有几个点电荷同时存在,它们的电场就互相叠加形成合电场.这时某点的场强等于各个电荷单独存在时在该点产生的场强的矢量和.(1)同一直线上电场叠加,E 合=E 1±E 2(同向则应相加,异向则应相减).(2)不在同一直线上电场叠加,E 合用平行四边形定则求解.以上是求合场强最基本的方法,求合场强还有一些技巧型的方法如:对称法、补偿法、等效替换法、极限法、特值法、微元法等.【经典例题选讲】【例题1】(2018·衡水模拟)如图所示,N (N >5)个小球均匀分布在半径为R 的圆周上,圆周上P 点的一个小球所带电荷量为-2q ,其余小球带电量为+q ,圆心处的电场强度大小为E 。
若仅撤去P 点的带电小球,圆心处的电场强度大小为()A .E B.E 2C.E 3D.E 4解析:选C 假设圆周上均匀分布的都是电荷量为+q 的小球,由于圆周的对称性,圆心处场强为0,则知在P 处带电量+q 的小球在圆心处产生的场强大小为E 1=k qr 2,方向水平向左,可知圆周上其余小球在O 处产生的场强大小为E 2=E 1=k qr 2,方向水平向右,带电量为-2q的小球在圆心处产生的场强大小为E 3=k2qr 2,方向水平向右。
根据叠加原理E =E 2+E 3,则k q r 2=E 3,所以撤去P 点的小球后,圆心处场强大小为E3,C 正确。
【变式1】(2018·抚顺期中)如图所示带正电的金属圆环竖直放置,其中心处有一电子,若电子某一时刻以初速度v 0从圆环中心处水平向右运动,则此后电子将()A .做匀速直线运动B .做匀减速直线运动C .以圆心为平衡位置振动D .以上选项均不对[解析]将圆环分成无数个正点电荷,再用点电荷场强公式和场强叠加原理求出v 0方向所在直线上的场强分布即可。
由场强叠加原理易知,把带电圆环视作由无数个点电荷组成,则圆环中心处的场强为0,v 0所在直线的无穷远处场强也为0,故沿v 0方向从圆心到无穷远处的直线上必有一点场强最大。
电场的叠加原理

电场的叠加原理
电场的叠加原理是指当有多个电荷体同时存在时,它们各自产生的电场可以独立地叠加。
也就是说,对于一个空间中的某一点而言,由多个电荷体产生的电场矢量可以根据矢量叠加原理进行叠加来求得。
假设有n个电荷体,每个电荷体的电荷量分别为q1、q2、…、qn,位置分别为P1、P2、…、Pn。
对于某一点P而言,各个
电荷体产生的电场矢量可以表示为E1、E2、…、En。
根据叠加原理,P点的合成电场E可以表示为各个电场矢量的
矢量和:
E = E1 + E2 + … + En
其中,每个电场矢量的大小和方向由库仑定律给出:
Ei = K * (qi / r^2) * ri
其中,K为库仑常数,r为P点到电荷体Pi的距离,ri为由电
荷体Pi指向P点的单位矢量。
注意,电荷体产生的电场矢量
的方向是由正电荷指向负电荷的方向。
通过将所有电荷体产生的电场矢量E1、E2、…、En进行矢量
叠加,可以求得P点的合成电场E的大小和方向。
需要注意的是,叠加原理只适用于电场是线性介质中的情况。
当介质不是线性时,例如介电常数不是常量或存在磁场时,电场的叠加原理可能不成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◎味知、擊
Northeastern University
1、点电荷系的场强
n
••• F = F + F +
Nቤተ መጻሕፍቲ ባይዱ+
Fn
=
i=1
F
E= F
q。
5 F
q
。
F
+
Fn
H-----F
=
q。
q。
n
土
=丄 Ei =丘
Q
ei
q o 4n% r1
= E2 F =—Q
q o 4ns0 r2
Ei =
Fi =__Q1
q o 4 兀8。F: ei
体分ns0布
—e 2 er
电场强度叠加原理1
— E=
f 4(f)
dq
_—r 匸re 2
电荷体密度p : dq = pdV
◎味知、擊
Northeastern University
电场强度叠加原理1
亓_ 1 dq 一
=总面戸分e 布
— E = f
如(V)
dq
_—r 匸re 2
电荷面密度。:dq = adS
(轴的方向:指向+0的矢量)
电偶极矩(电矩):p = qr0
+q
ro
家知、擘
Northeastern University
电场强度叠加原理1
计算轴线延长线上一点的电场强度
瓦1
4ne0
E
1
qI
+ 4 ne0
2
(X
亠 E E
q
+ 4 ne0
E
十
-q
+q O e ro/2
X
2 xr
(x 2
r2 )2 i
丘=瓦+瓦"•+f
Q瓦
电场强度叠加原理1
场强叠加原理a
味比人擘
Northeastern University
电场强度叠加原理1
电偶极子的电场强度
电偶极子:
两个相距的等量异号点电荷+0和-0,它们在空间产 生
电场。若场点到这两个点电荷的距离比,0大得多,这两
个点电荷构成的电荷系称为电偶极子
电偶极子的轴:r0
电场强度叠加原理1
2、连续分布电荷的场
强
把带电体看作是由许多个电荷元
LdV
组成,再利用场强叠加原理。
’、、、、亍 、\、P
任取体积元dV,视为点电荷
dE = 呉 e
dE
根据场强叠加原理
4兀爲r
J)奸 Ao!
dq _
—e r
◎味知、擊
Northeastern University
dE = 1 dq
4 一r
,视为点电荷,电量
为:
A 人=纟,dq =
dx dE ,
=—— 衅;
L
4n% x
Northeastern University
电场强度叠加原理1
电场强度叠加原理a
Principle of superposition of electric field indensity 电场强度E = F qo
- 10点电荷电场强度服菽戸乌
思考:多个点电荷产生的电场以及带电体 产 生的电场如何计算
4
A
E E十 X
◎莉濟、’
电场强度叠加原理1
E = -^ 4 n%
2 xr
•
2
(x 2 -当)2
L4
X r0, E =
i = 1 2P
4 m0 x5 4 n% X 3
O +q
0 2 ro/
X
-->A
_ E
X
金冢比六擊
_______ _________________________
Northeastern University
J r 1 adS 一
E s戒戸%
题 £比大学
电场强度叠加原理1
例1 设有一均匀带电直线段长度为Z,总电荷量为Q,
求其延长线上一点户电场强度.
_________F---------------X --------------A P
解:X <----1 丨— dx
L 二----T 0 dE
a0
力 建坐标系,在坐标为x处取一线元
