11第十一讲 条件平差习题课
平差(教学课件)-成晓倩-第1章内容总结及权习题

X
0 n
)
(二次以上项)
K k1
k2
kn
(
f X
1
)
0
(
f X
2
)
0
(
f X
n
)
0
n
k0
f
(
X
0 1
,
X
0 2
,
,
X
0 n
)
k
i
X
0 i
i 1
Z k1X1 k2 X 2 kn X n k0 KX k0
二、全微分法:
dX i
Xi
X
0 i
(i 1,2, , n)
dX (dX1 dX 2 dX n )T
线性函数
Z Y
KX FX
K0 F0
DZZ DYY DZY
KDXX K T FDXX F T KDXX F T
DYZ
F DX X
KT
QZZ QYY
KQXX K T FQXX F T
QZY
KQ XX
F
T
QYZΒιβλιοθήκη FQXX K T协方差传播律
协因数传播律
广义传播律
内容总结
7.两个传播律
hAB
N
2 站
pi
C Ni
测站高差精度相同时,水准测量高差的中误差与测 站数的平方根成正比,权与测站数成反比
hAB S 公里
pi
C Si
各测站距离大致相等时,水准测量高差的中误差 与距离的平方根成正比,权与距离成反比
内容总结
9.测量中的具体应用
二、同精度独立观测值的算术平均值
x
N
pi
平差习题集

1. 误差来源,测量平差的任务,多余观测的目的。
2. 试用公式说明方差协方差阵与协因数阵之间的关系?协因数阵与权阵之间的关系?在什么情况下它们为对角矩阵?若协因数阵为单位阵表示什么意思? 3. 已知随机变量y 、z 都是观测值L=[L1、L2、L3]T 的函数,函数关系如下:3162101733241L L L z L L L y +-=++=,已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=420231012LLQ ,证明y 、z 间互不相关。
4. 已知间接平差的模型为V=BX-L ,已知观测值的中误差为Q LL ,试推导Q VV 。
5. 已知独立观测值L 1,L 2的中误差为σ1和σ2,试求下列函数的中误差: (1)122X L L =- (2)211212Y L L L =+6. 某平差问题有15个同精度观测值,必要观测数为8,现选取8个参数,且参数之间有2个限制条件。
若按附有限制条件的条件平差法进行平差,应列出多少个条件方程和限制条件方程?由其组成的法方程有几个?7. 在相同条件下,观测两个角度∠A=30︒00'00",∠B=75︒00'00",设对∠A 观测6个测回的权为1,问观测∠B 9个测回的权为多少?8. 在相同观测条件下,应用水准测量测定点A —B —C —D 之间的高差,设路线长度分别为S 1=2km ,S 2=4km ,S 3=6km ,令12km 的高差观测值权为单位权观测,设每公里观测高差中误差为σ,试求各段观测高差之权及单位权中误差。
9. 取一长度为d 的直线之丈量结果的权为1,则长度为D 的直线之丈量结果的权为多少?若长度为D 的直线丈量了n 次,则其算术平均值的权为多少?。
10. 已知一水准网如下图,其中A 、B 为已知点,观测了8段高差,若设E 点高程的平差值与B 、E 之间高差的平差值为未知参数21ˆˆX X 、,按附有限制条件的条件平差法(概括平差法)进行平差时,必要观测个数为 ,多余观测个数为 ,一般条件方程个数为 ,限制条件方程个数为C11. 在已知水准点A 、B (其搞成无误差)间布设设水准线路,如图所示。
平差习题库

一、填空题:1、观测条件由观测仪器、____________和_____________三部分构成。
2、观测误差按其性质的不同可分为系统误差和偶然误差,其中____________误差在观测或计算过程中可以采用一定的措施消除或削弱,而___________误差在观测结果中必然存在。
3、测量平差的首要任务是经过数据处理,确定观测值的________________,而__________________________________________也是其必不可少的任务。
4、偶然误差的统计规律性是指:界限性、_______性、_______性和_______性。
5、在某相片上量得一距离长为200㎝,其相对中误差为1/3000,则该距离的绝对中误差为_____________________㎝。
6、测量平差是在______________的基础上利用_______________原理进行的。
7、单位权中误差mo、权Pi和中误差mi之间的关系为_______________________。
8、有一四边形导线环,同精度观测其各内角,共观测5组结果,计算出5个闭合差为﹣8″、9″、7″、﹣5″、-7″,则每组观测值之和中误差为____________,每个导线角观测值中误差___________。
(保留一位小数)9、设某角度观测值的协因数为3,则其观测值的权为_________。
10、观测成果的质量高低__________(能、否)反映观测条件的好坏。
11、理论上我们取3倍中误差为极限误差;而等级控制测量因为观测的精度要求比较高,往往规定______倍中误差为极限误差12、衡量精度常用的几种指标有中误差、___________误差和__________误差。
13、精度是指误差分布的________________程度。
14、由三角形闭合差ω计算测角中误差mβ的公式为______________________。
条件平差原理

§9.1 条件平差原理在条件观测平差中,以n 个观测值的平差值1ˆ⨯n L 作为未知数,列出v 个未知数的条件式,在min =PV V T 情况下,用条件极值的方法求出一组v 值,进而求出平差值。
9.1.1基础方程和它的解设某平差问题,有n 个带有相互独立的正态随机误差的观测值 ,其相应的权阵为 , 它是对角阵,改正数为 ,平差值为 。
当有r 个多余观测时,则平差值 应满足r 个平差值条件方程为:⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n (9-1) 式中i a 、i b 、…i r (i =1、2、…n )——为条件方程的系数;0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ(i =1、2、…n )代入(9-1)得条件方程(9-2)式中a w 、b w 、……r w 为条件方程的闭合差,或称为条件方程的不符值,即(9-3) 令⎪⎪⎪⎪⎪⎭⎫⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ2111⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L则(9-1)及(9-2)上两式的矩阵表达式为0ˆ0=+A LA (9-4) 0=+W AV (9-5)上改正数条件方程式中V 的解不是唯一的解,根据最小二乘原理,在V 的无穷多组解中,取PV V T = 最小的一组解是唯一的,V 的这一组解,可用拉格朗日乘数法解出。
平差(教学课件)-成晓倩-第3章条件平差

法方程纯量形式
NK W 0
K N 1W
aa ab ar p k a p k b p k r wa 0 ab bb br p k a p k b p k r wb 0 ar br rr k k k w 0 r p a p b p r
f f1 , f 2 ,, f n
T
f f f , ,, L ˆ ˆ L ˆ ˆ ˆ L ˆ L 1 2 n L L L L L
T
QFF f T Qf ( AQf )T N 1 ( AQf )
AV W 0
W ( AL A0 )
闭 合 差
函数模型
一、条件平差原理
AV W 0
W ( AL A0 )
乘系数
构造拉格 朗日函数
V T PV 2K T ( AV W )
K [k a
r ,1
k b k r ]T
一阶导数
( K T AV ) d (V T PV ) 2 2V T P 2 K T A 0 dV V V
一、条件平差原理
K N 1W
平差值
ˆ L V L
V P 1 AT K
NK W 0
R( N ) R( AP1 AT ) r
条件平差法方程的个数=多余观测个数r
内 容 安 排
一、条件平差原理
二、精度评定 三、不同几何模型的条件方程
四、公式汇编
二、精度评定
附有参数的条件平差法方程法方程法方程华北科技学院习题附

1
法方程:1
2
2
x2
8
0
\
3 2 0Ks 5
华北科技学院
第9章习题
5、
v1 v2
v1
v3 v4 v4 v5
5 0 6 0 3 0
v1
xˆ
0
试问: (1)以上函数模型为何种平差方法的模型? (2)本题中,n,t,r,c,u,s分别是多少?
A V B xˆ W 0
cn n1 cu cu c1
C
su
xˆ
u1
Wx
s1
0
法方程
NBaaTKK
Bxˆ CT
W 0 Ks 0
Cxˆ Wx 0
华北科技学院
第9章习题
某平差问题有12个同精度观测值,必要观测数t
= 6,现选取2个独立的参数参与平差,应列出多 少个条件方程?
HA X1 X2 X3 - HB 0
间接平差:
h1 X1
h2 X1 HB - HA
h3 X3 HB - HA
华北科技学院 h4 X3 ,h5 X2
第9章习题
(2)u=2.不独立 附有限制条件的条件平差 r+u=5
h1 X1 0
h2 X2 0
h1 h5 h3 0
h2 h5 h4 0
HA X1 X2 HB 0
华北科技学院
第9章习题
2、A,B为已知点,C为
11第十一讲 条件平差习题课
6.指出图示导线网按条件平差时条件方程的总数及 各类条件式的个数。
0
v3
(2)法方程及其解 Naa
K (3)求改正数V
V=
(4)求各观测值的平差值 Lˆ1 Lˆ2 Lˆ3
2.如图所示,设A点的 高程为100.000m,各测段的 观测高差及路线长度分别为:
h1 1.335m h2 1.055m h3 2.396m
S1 2km S2 2km S3 3km
试用条件平差法求 P1 、P2 点的高程平差值(观 测值改正数及条件式闭合差以mm为单位)。
(1)列条件方程
v1
v2
0
v3
(2)观测高差的权(以2km观测值的权为单位权)
P1
P2
P3
(3)组成并解算法方程
Naa K
(4)求各观测值的平差值及待定点的高程平差值
Lˆ2
Lˆ3
xˆ2
3.指出图示自由 测角网按条件平差时 条件方程的总数及各 类条件式的个数。
4.指出图示非自由 测角网按条件平差时条 件方程的总数及各类条 件式的个数。
5.指出图示非自由 测角网按条件平差时条件 方程的总数及各类条件式 的个数。
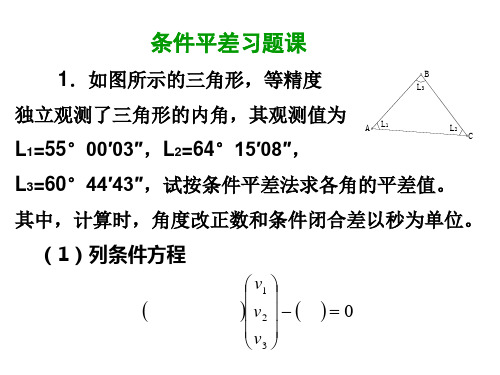
条件平差习题课
1.如图所示的三角形,等精度
独立观测了三角形的内角,其观测值为 A L1
L1=55°00′03″,L2=64°15′08″,
B L3
L2 C
L3=60°44′43″,试按条件平差法求各角的平差值。
其中,计算时,角度改正数和条件闭合差以秒为单位。
(1)列条件方程
vHale Waihona Puke v2
测量平差习题

第一章观测误差与传播率第一节观测误差1、在下列情况下用钢尺丈量距离,使量得的结果产生误差,时判别误差的性质与符号:(1)尺长不准确;(2)尺长检定过程中,尺长与标准尺长比较产生的误差;(3)尺不水平;(4)尺反曲或垂曲;(5)尺端偏离直线方向;(6)估读小数不准确;2、在下列情况下使水准测量中水准尺的读数带有误差,试判别误差的性质与符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沉;(5)水准尺竖立不直。
第二节衡量精度的指标3、为检定某经纬仪的测角精度,对已知精确测定的水平角α=58002’00.0”(无误差)进行10次观测,其结果为:58002’03” 58002’01” 58001’58” 58001’57” 58002’04”58001’59” 58001’59” 58002’05” 58002’01” 58001’57”试求测角中误差σ。
4、设有两组观测值X i和Y i,它们的真误差分别为:△x:2,-3,+1,0,+2 △y:0,+3,+1,-2,+3试求观测量X与Y的方差σx2和σy2,哪个测量观测精度高?5、某距离在相同的观测条件下观测20次,得独立观测值(单位:m)为:437.59 437.61 437.60 437.55 437.59 437.62 437.64 437.62437.64 437.61 437.69 437.63 437.61 437.62 437.61 437.60437.56 437.68 437.65 437.58试计算该距离的算术平均值X及其方差与中误差估值。
6、有两段距离S1和S2,经多次观测得观测值及其中误差分别为300.00±2cm和600.00±2cm,试问哪段距离观测精度高?二距离各次观测值的观测真误差是否相同?7、有一段距离,其观测值及其中误差为652.48m±9mm。
(1)试估计该观测值的真误差实际可能出现的范围是多少?(2)试求该观测值的相对中误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
v3
(2)法方程及其解 Naa
K (3)求改正数V
V=
(4)求各观测值的平差值 Lˆ1 Lˆ2 Lˆ3
2.如图所示,设A点的 高程为100.000m,各测段的 观测高差及路线长度分别为:
h1 1.335m h2 1.055m h3 2.396m
S1 2km S2 2km S3 3km
试用条件平差法求 P1 、P2 点的高程平差值(观 测值改正数及条件式闭合差以mm为单位)。
(1)列条件方程
v1
v2
0
v3
(2)观测高差的权(以2km观测值的权为单位权)
P1
P2
P3
(3)组成并解算法方程
6.指出图示导线网按条件平差时条件方程的总数及 各类条件式的个数。
Naa K
(4)求各观测值的平差值及待定点的高程平差值
Lˆ2
Lˆ3
xˆ2ห้องสมุดไป่ตู้
3.指出图示自由 测角网按条件平差时 条件方程的总数及各 类条件式的个数。
4.指出图示非自由 测角网按条件平差时条 件方程的总数及各类条 件式的个数。
5.指出图示非自由 测角网按条件平差时条件 方程的总数及各类条件式 的个数。
条件平差习题课
1.如图所示的三角形,等精度
独立观测了三角形的内角,其观测值为 A L1
L1=55°00′03″,L2=64°15′08″,
B L3
L2 C
L3=60°44′43″,试按条件平差法求各角的平差值。
其中,计算时,角度改正数和条件闭合差以秒为单位。
(1)列条件方程
v1 v2
