NS方程的非结构化网格方法及其差分格式
【国家自然科学基金】_非结构混合网格_基金支持热词逐年推荐_【万方软件创新助手】_20140802

推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 混合网格 非结构网格 子弹簧系统 动态网格 ball-vertex弹簧法 高阶精度格式 间断伽辽金方法 质量优化 网格自适应 网格粗化 网格生成 结构网格 粘性绕流计算 粘性流动 粒子成像测速 稀薄过渡流 离心泵 直角网格 有限谱差分方法 有限谱体积方法 有限体积方法 无网格方法 数值模拟 并行算法 多段翼型 喷流干扰 ns方程 dsmc方法 dg/fv混合算法
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 非结构网格 钝体驻定火焰 粒子输运 火焰面模型 激波捕捉 混合算法 欧拉方程 概率密度函数方法 旋转riemann求解器 多维格式 多核机群系统 基于特征线方程的分离算法 前沿推进 sn方法 riemann邶求解器 mpi/openmp混合并行计算 delaunay三角化 "红斑"现象
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 混合网格 非结构网格 非定常运动 非定常计算方法 结构网格 水平井 有限体积法 数值试井 动态网格技术 几何守恒率 井模型 pebi网格
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
二维NS方程无结构网格并行计算

,,&) ‘  ̄r 】 。P = , i【二丁,  ̄ 又
可得最佳梯度: 让f取极小,
E( 。 (一) PJ . ‘ ,
( 6)
3
御1
&C
I
{一 一一r,‘ [ 、 (YX一} ( ) Y',甲 、 。 ') ) i ,
12 r 1: i 1 一z 1 z r
工作 。
图1 结构剖分网格的区域分解
30 9
图2 无结构网格区域分解
22并行计算 .
本文的并行工作是在CRE高性能计算中心的S2 ENT P计算机上, 采用四个节点进行计算, 利
用M I P 函数实现各个节点之间的通讯。
3计算结果
本文采用上述格式在S2 P上进行了 A 22翼型的绕流计算。 R E 82 分别针对较粗网格和细网 格 进行了计算,下面图 和图 给出了计算的 3 4 细网 格以 及粗、 细网 格计算结果和实验的比 较,结 果表明加密网格可以得到与实验更加吻合的结果。通过计算表明,本文采用的计算方法可以 有效地应用于 S N 方程的计算中,而采用并行计算可以 提高计算的效率并可以 克服单机内存不 足的缺陷。由 无结构网格的结构复杂性, 于 本文采用四 个节点的并行效率接近3 还需要进一 , 步的努力,以提高C U的利用效率。 P
张 信・ 波动 无自 今数的 敞 分格 空 动力 学 9 1) n H . N den s ee rl 涵 无 、 由 耗 差 式, 气 学 报18 ( a X N D r c c m , ao 8 ( Z g , i e e 1 h f h Jn f o u
第 A m 丝 f 堂创 i 十全丝A 逐色一一一一一一一一一一一
二维NS -方程无结构网格并行计算
徐听 符松
模拟casson流体的非结构化网格simple算法

模拟casson流体的非结构化网格simple算法非结构化网格算法是一种用于模拟高复杂度流体流动的数值方法。
它已成功应用于模拟Casson流体的研究。
Casson流体是一种悬浮流体,具有十分复杂的粘弹性性质和粘性,其可塑性比一般流体要大。
因此,精确模拟Casson流体流动的计算过程较为复杂,传统的结构化网格CSG(Computational Structured Grid)数值模拟方法难以满足其误差要求,因此非结构化网格算法(Unstructured Grid)会非常有效。
非结构化网格算法主要包括多种算法,如Delaunay Triangulation(DT)、Voronoi Diagram(VMD)和Simple Polygon Representation(SPR),以及基于特征曲线的算法等。
Simple算法是其中比较简便的方法,它通过建立和更新网格,构建紧凑的网格单元,使模拟的结果尽可能精确。
Simple算法由两个阶段组成。
第一个阶段是构建模拟场所需要的非结构化网格。
注入物理空间盒子中,先将已知边界和控件网格单元按已知几何空间形状建立,然后再填充内部扩充到未知面的随机网格单元,提高该空间网格的精度和复杂度,以完成模拟。
第二个阶段是更新非结构化网格单元,使它们更加紧凑,以满足模拟的要求。
重新排列网格单元的顺序,使其与物理る空间的几何形状保持更为一致,从而降低误差。
结合Simple算法,可用于计算Casson流体流动方程,模拟Casson流体具有耦合性质的流动情况。
Simple算法可以更好地反映流体流动的实际情况,更精确地处理流体流动现象,使研究者在复杂流体流动环境中获得更准确的结果。
另外,由于该方法的算法简单,模拟的精度高,因此被广泛应用到研究Casson悬浮流体的研究中。
非结构网格的LU-SGS隐式算法在浅水方程组中的应用的开题报告

非结构网格的LU-SGS隐式算法在浅水方程组中的应用的开题报告一、选题背景浅水方程组是描述流体在水平方向上流动的方程组,广泛应用于海洋、大气、湖泊等自然环境中。
由于其耦合性强、非线性大、空间尺度差异性明显等特点,目前尚未找到一种通用的数值求解方法。
在数值计算中,网格的生成和处理一直是一个非常重要的问题。
对于常规方法来说,网格的划分和重构的复杂度非常大,而且不利于处理几何结构复杂的区域。
非结构网格的应用则能够有效解决这些问题。
为解决浅水方程组的数值求解问题,应用非结构网格的LU-SGS隐式算法进行求解具有重要的应用价值。
二、相关工作目前,对于浅水方程组的求解方法主要有传统有限差分法、有限体积法、有限元法等。
这些数值方法通常需要使用结构化网格,并不能很好地刻画复杂的地形和海洋环境。
近年来,基于非结构网格的方法受到广泛关注,例如有限元、有限体积和谱方法等。
LU-SGS隐式算法是目前非结构网格求解方法中最常用的一种。
由于其具有稳定性和效率的优势,已被广泛应用于模拟流体动力学、天气预报、海洋气象等众多领域。
隐式求解方法的一个重要优势是可以处理比显式方法更长的时间步长,从而减少计算量和存储量。
三、研究内容和方法本文旨在使用非结构网格的LU-SGS隐式算法对浅水方程组进行数值求解,并探究其应用效果。
具体研究内容和方法如下:1.构建浅水方程组的数学模型。
2.建立非结构网格,并使用有限体积法或有限元法离散方程组。
3.采用LU-SGS隐式算法进行数值求解,并进行稳定性分析、误差分析及收敛性分析。
4.基于仿真结果进行分析和讨论,验证所提算法的有效性和优越性。
四、创新点和意义本研究的创新点和意义在于:1.提出非结构网格的LU-SGS隐式算法求解浅水方程组的方法,有效解决了传统数值方法中对结构化网格的需求限制问题。
2.所提方法具有实际应用价值,可广泛应用于海洋、大气、湖泊等自然环境中的数值模拟。
3.能够提高数值方法的效率和精度,具有重要的科学研究和工程应用价值。
流体力学ns方程怎么积分_概述说明以及解释

流体力学ns方程怎么积分概述说明以及解释1. 引言1.1 概述流体力学是研究流体运动和力学行为的学科,广泛应用于各个领域,包括航空航天、汽车工程、海洋工程等。
在流体力学中,Navier-Stokes(NS)方程被认为是描述流体的基本方程之一。
NS方程描述了流体在三维空间中的质量守恒、动量守恒以及能量守恒。
由于NS方程的复杂性和非线性特性,解析求解NS方程变得十分困难,因此需要借助数值积分方法进行求解。
1.2 文章结构本文将以“流体力学NS方程怎么积分”为主题,探讨NS方程的积分方法。
文章结构如下:引言:介绍研究背景、文章概述以及目的。
流体力学NS方程概述:详细介绍什么是流体力学NS方程以及其基本形式和含义,阐述其应用范围和重要性。
NS方程积分方法总览:概述基本求解方法和数值模拟技术,并介绍常见的NS 方程数值求解算法和逼近方法。
NS方程积分详解及其实践应用:详细说明将NS方程离散化为有限差分形式的步骤和原理,讨论不同类型流体问题的积分方法,并介绍已有工具包和软件在流体力学中使用NS方程进行模拟研究的案例。
结论与展望:总结已经阐述过的内容,展望NS方程积分方法的发展趋势,并讨论对NS方程积分的理解以及未来可能的应用前景。
1.3 目的本文旨在概述并解释流体力学中NS方程的积分方法。
通过对基本求解方法、数值模拟技术以及常见数值求解算法和逼近方法等进行总览和详解,希望读者可以全面了解NS方程积分的原理和实践应用。
同时,通过介绍已有工具包和软件在流体力学研究中使用NS方程进行模拟的案例,展示该方法在实际问题中的应用价值。
最后,我们将对NS方程积分方法未来发展趋势进行展望,并总结对于NS方程积分的理解与未来可能的应用前景。
2. 流体力学NS方程概述:2.1 什么是流体力学NS方程流体力学Navier-Stokes(NS)方程是描述流体运动的基本方程之一。
它由欧洲科学家Claude-Louis Navier和George Gabriel Stokes提出,并以他们的名字命名。
高等计算流体力学讲义(8)

高等计算流体力学讲义(8)第三章 不可压缩流动的数值方法§1 基本方程及其性质一、基本方程考虑不可压缩NS 方程: 0∇=u(1)()p tρρρτ∂+∇=-∇+∇∂u uu f(2)其中粘性应力为, 2τμ=S(3)12()T=∇+∇S u u如果粘性系数为常数,τμ∇=∆u (4)经无量纲化,常粘性系数不可压缩NS 方程可以写为:()p tυ∇=∂+∇=-∇+∆∂u u uu f u,其中/υμρ=为运动粘性系数。
NS 方程也可以写为无量纲化形式01()R ep t∇=∂+∇=-∇+∆∂u u uu f u其中ρ已经吸收到p 中(p 代表/p ρ)。
不可压缩方程的边界条件为:固体壁面:wall =u u , 进口条件:in =u u ,出口条件:n∂=∂u 0。
不可压缩方程中的压力场可以相差任一常数而对速度场无影响,所以压力场只是在相差任意常数的条件下是确定的。
为了确定全场压力值,还应指定流场中某一点的压力。
二、不可压N -S 方程的特点:(1) 方程为二阶偏微分方程,二阶项中包含参数μ(粘性系数)。
边界层、分离、湍流…(2) 方程是非线性的,表现为对流项()∇uu 。
对一维问题,非线性项为u ux∂∂。
假定u 的波数为k 的Fourier 分量为()s i n u u t k x = (5) 则:21sin 22u uukx x∂=∂ 。
即振幅由212u u→ ;波数由2k k →。
也就是说,振幅呈现非线性变化,且可以产生高频成分。
粘性的作用,使得解的结构进一步复杂化,考虑模型方程221Re u u tx∂∂=∂∂把(5)式带入模型方程,得2(/Re)()k tut e -=可见,雷诺数越大,或频率越低(流动结构的尺度越大),振幅衰减越慢。
综上所述:由于非线性的作用,会产生高频的流动结构;在大雷诺数的条件下,这些高频结构有较长的生命周期,并且与衰减缓慢的低频结构相互作用,使得流动表现出复杂的的非线性、多尺度特征。
【计算流体力学】第5讲-差分方法3
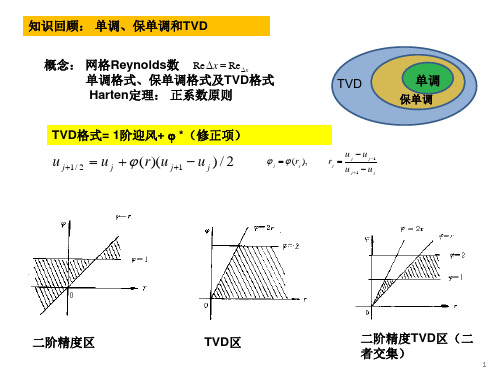
通量差分分Байду номын сангаас (FDS): 耗散低、分辨率高
Step 1: 运用差分格式,计算
U ,U L j 1/ 2
R j 1/ 2
Step 2: 运用Riemann解, 计算
F j 1/ 2
F
(U
L j 1/
2
,U
) R
j 1/ 2
Step 3: F Fj1/2 Fj1/2
x
x
U ,U L j 1/ 2
R j 1/ 2
f
j 1/
2
x
x
f f + f =+
x x x
13
3. 特征重构方法
常系数方程组:
U t
A U x
0
U t
S1ΛS U x
0
V t
Λ V x
0
vk t
k
vk x
0
变系数情况—— 局部冻结系数
完全 解耦
U f(U) 0 U A U 0
t x
t x
在基架点上系数 A j 不变
U t
u j u j1 u j1 u j
二阶精度区
TVD区
二阶精度TVD区(二 者交集)
1
通量分裂技术: 模型方程 NS/ Euler 方程
Step 1 针对模型方程构造差分格式
u a u 0 t x
u uˆ j1/2 uˆ j1/2
x
x
a0
uˆ j1/2 =......
格式1
a0
uˆ j1/2 =......
6
➢ Steger-Warming 具体步骤 (以一维为例)
u a u 0
t x
拉格朗日法ns方程

拉格朗日法ns方程
拉格朗日法(Lagrangian formulation)是一种在动力学中描述系统的方法,其中系统的状态由拉格朗日量(Lagrangian)来定义。
Navier-Stokes(NS)方程组是描述流体动力学中流体运动的方程。
拉格朗日法并不常用于描述整个Navier-Stokes方程组,而通常更适用于描述系统的特定动力学。
NS方程组描述了流体的质量守恒、动量守恒和能量守恒。
对于一个不可压缩、粘性的流体,NS方程组可以写成如下的形式:
使用拉格朗日法对整个Navier-Stokes方程组进行求解并不常见,因为NS方程组通常以欧拉法(Eulerian formulation)的形式进行表述。
欧拉法通过描述流体在空间中的固定点上的性质来分析流体动力学。
如果你有特定的问题或系统,可以提供更多详细信息,以便我能够更好地帮助你。
1/ 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安交通大学学报JOURNAL OF XI'AN JIAOTONGUNIVERSITY1999年 第33卷 第9期 Vol.33 No.9 1999NS方程的非结构化网格方法及其差分格式张楚华, 谷传纲, 苗永淼摘要: 采用同位非结构化网格上的有限体积法,对Navier-Stokes方程的SIMPLE算法及差分格式进行了研究.提出了适用于非结构化网格的不用求解单元顶点变量值的二阶混合差分格式.该格式的优点在于:1)减少了计算工作量;2)避免了普通混合差分格式因使用简单的一阶迎风差分格式所引起的网格界面方向相关性的问题.最后,采用三角形网格,利用提出的方法及差分格式,对方腔内的驱动层流及绕翼型湍流进行了数值计算,计算结果与基准解或实验值的符合程度优于普通混合差分格式.关键词: 非结构化网格;差分格式;有限体积法中国图书资料分类法分类号: O357Unstructured Grid Method and Its Differential Schemes for NS EquationsZhang Chuhua, Gu Chuangang, Miao Yongmiao(Xi′an Jiaotong University, Xi′an 710049, China)Abstract: The SIMPLE algorithm and differential schemes are used for solving Navier-Stokes equations through finite volume method with collocated unstructured grid. A two order hybrid scheme without the necessity of computing the variables at elements vertices is presented. Compared with the ordinary hybrid scheme, the advantages are :1)computation is reduced; 2) grid dependency problem, which is resulted from one order upwind interpolation in ordinary hybrid scheme on unstructured grid, can be avoided. Finally, the proposed method and schemes are used to calculate laminar flow in a lid-driven cavity and turbulent flow around an airfoil. The numerical results fit benchmark solutions and experiments better than those calculated through ordinary hybrid scheme.Keywords: unstructured grid;differential scheme;finite volume method 长期以来,人们一直认为有限差分法(包括有限体积法)对复杂形状流动问题的处理能力不如有限元法,近年来发展起来的非结构化网格方法[1,2]正逐步改变这一看法.在非结构化网格上利用有限体积法来求解流动方程, 既能提高有限体积法处理复杂形状流动问题的能力,又能保持离散方程的局部守恒特性,而后者对数值求解非线性偏微分方程的收敛过程有时是至关重要的. 在非结构化网格上采用有限体积法求解流场,是计算流体动力学中很有发展前途的研究方向.当然这一领域仍然有一些棘手的问题亟待解决和完善,其中主要包括:1)高质量的非结构化网格生成问题;2)非结构化网格方法的计算工作量问题;3)非结构化网格上高精度差分格式的实现问题;4)快速稳定的非结构化代数方程组的求解问题;5)在高伸展比的非结构化网格单元上实现稳定性、经济性俱佳的计算格式;6)自适应问题.本文对2)、3)、4)的问题进行了研究,提出了一种适合于在非结构网格上计算的差分格式,并对驱动方腔内的流动及孤立翼型绕流进行了数值模拟,得到了满意的数值结果.1 控制方程 本文研究的问题为二维、定常、不可压缩流动,控制方程可写成如下通用方程 (1)其中: U m为沿着坐标方向x m的速度分量; Φ为求解变量; ΓΦ为广义扩散系数;为广义源项.式(1)的具体形式见文献[3].2 计算方法2.1 通用方程的离散 利用Gauss定理,将控制方程(1)在任一边数为n的非结构化网格单元上离散为 (2)其中: ΔV为网格单元的体积.式(2)左端的第1部分为对流部分(ρVΦ.A)f=m fΦf (3)式(2)左端的第2部分为扩散部分,文献[2,4]分别利用局部非正交坐标系及Gauss定理推导出的扩散部分的离散形式为 (4)式(4)中的第1项为正交扩散项,第2项为非正交扩散项.式中出现了单元顶点处的变量值.其中下标f为界面;下标il、ir、ist、iend分别表示边f的左单元、右单元、起点、终点;σV为界面积分体积;n f为单位法向矢量; n i end为左、右单元连线的单位法向矢量. 式(3)与(4)中的m f为通过界面f的质量流量,引入Peclet准则,PΔ=m f/D f,其中D f 为通过界面的扩导,,则PΔ数表示输运量Φ通过界面f的对流和扩散能力的相对大小.这与结构化网格上的研究结果是相同的,因此可以借用结构化网格的思想来进一步得出通用方程在非结构化网格上的离散形式.然而,它们之间也存在很大的差异,主要表现在:1)界面上Φf的计算;2)非正交扩散项的计算.这两项的计算方式对非结构化网格方法的精确性及计算工作量的影响都很大. 在计算Φf时,由于非结构化网格拓扑结构的无规律性,在较粗的非结构化网格上应用简单的一阶迎风格式容易出现网格相关性问题,而一些在结构化网格上行之有效的高阶差分格式,如高阶迎风格式、QUICK格式、MUSCL格式等很难在非结构化网格上实施.这是因为在采用这些格式确定界面上的对流项时,需要知道远上游结点处的变量值,而在非结构化网格拓扑结构中,远上游结点属于“游荡结点”[2],无法从网格的拓扑结构中直接确定这些点的位置,只能在流场计算中,根据局部流动方向计算出远上游结点的位置,这给非结构化网格方法进一步增加了计算负担.本文根据线性重组建梯度方法及限制因子方法,提出了适合于非结构化网格上计算的二阶混合差分格式,界面上的变量计算公式为 (5)其中限制因子α根据文献[3]的方法计算,当α=0时,上式就退化为普通混合差分格式. 式(4)中,非正交扩散项出现单元顶点处的变量值,这些值一般由相邻单元中心处的变量值插值而来.常用的插值方法有面积加权插值、距离负幂次函数加权插值、最小二乘插值方法.前两种方法实现简单,计算速度快,但计算精度低;后一种方法具有二阶精度,但实现复杂,可能出现奇性问题,计算速度慢,数值计算表明,在每轮迭代计算中,约有一半时间花在利用最小二乘法插值各类变量在单元顶点值的计算上.本文利用界面梯度近似关系式(Φ)f=,其中表示线性插值运算,对式(4)中的非正交扩散项进行如下变换 (6)这样在非正交扩散项中不再出现单元顶点处的变量值,从而极大地减少了计算工作量,同时仍可以采用与结构化网格相同的处理方法,将正交项隐式处理,而将非正交项显式处理. 将式(3)、(5)、(6)代入式(2),即得 (7)对于任一单元P,可将式(7)归纳为 (8) A P=∑A nb A(PΔ)=A(|PΔ|)+[|-PΔ, 0|] B(PΔ)=A(PΔ)+PΔ A(|PΔ|)=[|0, 1-0.5|PΔ||]其中 [|,|]表示求最大值运算; Δr为左、右单元之间的长度矢量; f1表示线性插值因子.2.2 压力修正方程 本文采用SIMPLE算法求解压力,压力修正量p′的方程在形式上与式(8)完全相同,相应的系数为 为了进一步减少非结构化网格的计算工作量,本文采用以界面序号为循环变量而不是直接以单元序号为循环变量来离散流动方程;采用预条件矩阵共轭梯度平方法[5]来加速离散代数方程组的收敛速度.3 计算结果3.1 方腔内的驱动流动 对Re=1000时方腔内的驱动流动进行计算,与文献[6]相同,按层流计算.图1为计算网格,在方腔的每条边上布置21个结点,网格结点数Nn=504,边数Nl=1 429,单元数Ne=926,网格疏密程度相当于31×31的结构化四边形网格.图2为通过方腔几何中线上的流动速度分布.图3为方腔内流动的速度矢量图.从图2可以看出,在相同疏密程度的网格上,利用本文所提出的不用求解单元顶点处变量值的二阶混合差分格式比一阶混合格式更接近于基准解.图1 方腔内的计算网格 (a)水平向速度(b)竖直向速度-.-:一阶格式; ——:二阶格式; .:文献[6]图2 Re=1 000时方腔几何中心线上的流动速度图3 速度矢量(Re=1 000)3.2 孤立翼型绕流 对某大型轴流压缩机进口级动叶片中间截面的孤立翼型绕流进行了湍流数值计算.文献[7]给出了此翼型详细的几何尺寸及翼型表面压力的测量值,其中翼型弦长l=0.0824m,自由来流速度U∞=39.8m/s,翼弦雷诺数Re=2×105.图4为计算网格在翼型附近的局部放大图.计算区域为翼型上、下游与上、下区域分别延长5倍长的范围,计算区域为双连通区域,网格节点数N n=3061,边数N l=9041,单元数N e=5980.图5与图6分别为翼弦攻角为0°时翼型表面压力系数与翼型附近压力分布等值线图.由图可知,计算结果与实验值吻合很好.图4 孤立翼型绕流局部网格图5 翼型表面压力系数(i=0°)图6 翼型附近等压线(i=0°)4 结 论 (1)推导了同位非结构化网格上的SIMPLE算法,发现在非结构化网格上,Peclet 准则仍然是构造差分格式的基本出发点,这与结构化网格方法是一致的. (2)提出了一种适合于非结构化网格计算的不用求解单元顶点处变量值的二阶混合差分格式,该格式避免了普通混合差分格式在非结构化网格上容易出现网格相关性的问题,同时减少了计算工作量. (3)计算结果表明,本文提出的差分格式对数值解的准确性有所改善.作者简介: 张楚华,男,1967年10月生,能源与动力工程学院流体机械研究所,讲师.作者单位:张楚华, 谷传纲, 苗永淼 (西安交通大学, 710049, 西安)参考文献:[1] Jameson A, Mavriplis D. Finite volume solution of two dimensional Euler equations on a regular triangular mesh. AIAA J, 1986, 24(4): 611~618.[2] Sheng H M, Chen Y S. An unstructured grid method for flow computations at all speeds. 见:第六届全国计算传热学会议论文集.郑州, 1995. 35~44.[3] 张楚华.三维湍流流动的非结构化网格的数值解法及其在离心风机内的应用研究:[博士学位论文].西安:西安交通大学能源与动力工程学院, 1999.[4] Davidson L. A pressure correction method for unstructured meshes with arbitrary control volumes. International Journal for Numerical Methods in Fluids, 1996, 22(4): 265~281.[5] Sonneveld P. CGS, a fast Lanczos-type solver for nonsymmetric linear systems. SIAM J Sci Stat Comput, 1989, 10(1): 36~52.[6] Ghia U, Chia K N, Shin C T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J of Comp Phys, 1982, 48(3): 387~411.[7] 钱泽球.大型轴流压缩机组性能预测及设计方法的研究:[硕士学位论文].西安:西安交通大学能源与动力工程学院, 1993.收稿日期: 1999-01-08.(编辑 蒋慧姝)NS方程的非结构化网格方法及其差分格式作者:张楚华, 谷传纲, 苗永淼, Zhang Chuhua, Gu Chuangang, Miao Yongmiao作者单位:西安交通大学,710049,西安刊名:西安交通大学学报英文刊名:JOURNAL OF XI'AN JIAOTONG UNIVERSITY年,卷(期):1999,33(9)被引用次数:12次1.Ghia U;Chia K N;Shin C T High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method 1982(03)2.Sonneveld P CGS,a fast Lanczos-type solver for nonsymmetric linear systems 1989(01)3.Davidson L A pressure correction method for unstructured meshes with arbitrary control volumes[外文期刊] 1996(04)4.钱泽球大型轴流压缩机组性能预测及设计方法的研究[学位论文] 19935.张楚华三维湍流流动的非结构化网格的数值解法及其在离心风机内的应用研究[学位论文] 19996.Sheng H M;Chen Y S An unstructured grid method for flow computations at all speeds 19957.Jameson A;Mavriplis D Finite volume solution of two dimensional Euler equations on a regular triangular mesh[外文期刊] 1986(04)1.罗昔联.顾兆林.雷康斌.加濑究一种三维切削网格上的N-S方程离散方法[期刊论文]-西安交通大学学报 2010(5)2.罗昔联.顾兆林.雷康斌.加濑究一种求解N-S方程的自适应直角网格方法[期刊论文]-西安交通大学学报 2009(11)3.马薇.罗芳.梁武科带前置诱导轮的复合叶轮型离心泵数值分析[期刊论文]-电网与水力发电进展 2008(5)4.赵道利.梁武科.万天虎.马薇.吴广宽.廖伟丽灯泡贯流式水轮机轮缘间隙流动的数值模拟[期刊论文]-西安理工大学学报 2007(3)5.王宝潼.张楚华.席光.刘帆串列叶片式离心叶轮内流场的数值研究[期刊论文]-西安交通大学学报 2007(11)6.张楚华三维流体诱发振动的理论模型与数值模拟[期刊论文]-西安交通大学学报 2007(5)7.姜华.席光对流项二次迎风插值格式在非结构化网格中的应用[期刊论文]-西安交通大学学报 2006(11)8.范辉.曾凡棠.郭森水环境数值模拟-SIMPLE算法研究与进展[期刊论文]-环境科学与技术 2006(z1)9.朱斌与内弹道耦合的多管发射膛口非定常流场数值模拟[学位论文]硕士 200610.李荣非正交曲线坐标系下的温度场和流场的计算[学位论文]硕士 200511.钟世梁MPI环境下传热流动问题的并行数值计算[学位论文]硕士 200512.匡江红.史平洋.丁士发流动与传热数值模型的发展现状[期刊论文]-发电设备 2001(1)本文链接:/Periodical_xajtdxxb199909015.aspx。
