奥数-等腰三角形和等边△-第十讲教师版
奥数-等腰三角形和等边△-师

第十讲 等腰三角形和等边三角形一、 基础知识1.等腰三角形的性质及推论:(1) 等腰三角形的两底角相等(2) 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)(3) 等边三角形的各角都相等,并且每一个角都等于︒602.等腰三角形的判定及推论:(1)从定义入手,证明一个三角形的两条边相等(2)从角入手,证明一个三角形的两个角相等(3)有一个角为︒60的等腰三角形是等边三角形尤其要注意全等在等腰、等边三角形中的应用.二、名校真题回放1.(北京市西城区2006年抽样测试八年级(上)试卷)如图,在△ABC 中,AC AB =,它的周长为24,又BC AD ⊥于D ,△ABD 的周长为20,则AD 的长为多少?解答:82.(北京市西城区2006年抽样测试八年级(上)试卷)在等边三角形ABC 中,E D ,分别在边AC BC ,上,AE DC =,F BE AD 交于点,.请你判断ABE DAC ∠∠和的大小关系,并证明你的结论.解答:ABE DAC ∠=∠3.(北京市西城区2006年抽样测试八年级(上)试卷)已知:如图,△ABC 中,AC AB =,D 为AC 上一点,A DBC ∠=∠21.求证:BD AC ⊥ 解答:利用三角形内角和.4.(北京市西城区2006年抽样测试八年级(上)试卷)已知△ABC 的三边c b a ,,满足等式:02222=-+-bc ab c a ,试说明△ABC 是等腰三角形.解答:0)2)((=++-b c a c a5. (2006年海淀区八年级第一学期期末测评)如图为一张梯形纸片ABCD ,AD ∥BC ,︒=∠90BDC .将其沿对角线BD 翻折后压平,AD 和'BC 相交于点E ,则图中的等腰三角形有__________________,_________________(只写出两个正确结论)解答:△BED ,△'BCC 等等.三、活题巧解(一)等腰三角形的性质例1.(2001年湖州市中考题)如图,在△ABC 中,BC AC C =︒=∠,90,AD平分CAB ∠交BC 于D ,AB DE ⊥于E ,若AB =6cm ,则△DEB 的周长是多少?解答:6cm例2.(2002年上海市竞赛题)如图,BD AC ,相交于E ,AC 平分DAB ∠,且AC AD AE AB ==,,有以下四个结论:(1)BD AC ⊥;(2)DE BC =;(3)DAB DBC ∠=∠21;(4)△ABE 是等边三角形.其中正确的结论是什么? 解答:(2)(3)例3.(1996年连云港市中考题)在△ABC 中,AC AB =,P 为三角形内一点,APC APB ∠<∠,则PBC ∠与PCB ∠的大小关系如何?解答:作BAP CAQ ∠=∠,并使得AP AQ =,连接CQ ,得到PBC ∠<PCB ∠例4.(第11届“希望杯”试题)如图,在△ABC 中,︒=∠==60,4,2ACB BC AC ,将△ABC 折叠,使得点B 和点C 重合,折痕为DE ,则△AEC 的面积是多少?解答: 332 例5.(2004年洛阳市中考题)用一根长为a 米的线围成一个等边三角形,其面积为b 平方米,现在这个等边三角形内任取一点P ,则点P 到等边三角形三边的距离之和是多少米?解答:ab 6米例6.(1997年天津市竞赛题)如图,△ABC 是边长为1的等边三角形,CD BD BDC =︒=∠,120,点N M ,分别在AC AB ,上,且︒=∠60MDN ,连结MN ,求证:△AMN 的周长等于2.解答:延长AC 至E ,使BM CE =,连结DE .先证△BMD ≌△CED ,再证△MDN ≌△EDN .例7.(2000年无锡市竞赛题)在△ABC 中,AC AB =,过△ABC 某一顶点的直线可将△ABC 分成两个等腰三角形,试求△ABC 各内角的度数.解答:共有4种情况,其内角相应度数为)7540,7540,7180(),72,72,36(),108,36,36(),90,45,45(︒︒︒︒︒︒︒︒︒︒︒︒(二)等腰三角形的判定例8.(2002年泰州市中考题)如图,在△ABC 中,AC AB =,︒=∠36A ,CEBD ,分别为ACB ABC ∠∠,的角平分线,且相交于F ,则图中的等腰三角形有几个?解答:8个例9.(2003年长春市中考题)在△ABC 中,C B ∠=∠2,则AC 与AB 2之间的大小关系是什么? 解答:作D BC C CAD 于交∠=∠,得到AB AC 2<例10.(1999年江苏省竞赛题)已知△ABC 是等边三角形,E是AC 延长线上的任意一点,△CDE 也是等边三角形,若NM ,分别是线段BE AD ,的中点,求证:△CMN 是等边三角形.解答:先证△ACD ≌△BCE ,再证△DCM ≌△ECN ,得到︒=∠=60,NCM CN CM例11.(1996年北京市竞赛题)三角形三边长c b a ,,满足c b a c b a +-=+-1111,则三角形一定是( ) A.等边三角形 B.以a 为底边的等腰三角形C.以c 为底边的等腰三角形D.等腰三角形解答:把原式恒等变形,得到0))()((=+--c a b a c b ,故选D.例12.(第3届“希望杯”试题)等腰三角形的周长为a ,一腰的中线将周长分成3:5的两部分,则此三角形的底边长是多少?解答:分情况讨论,两种情况里舍去一种,解得底边长为a 61 例13.(2001年唐山市中考题)如图,在△ABC 中,AC AB =,D 为△ABC外一点,,60︒=∠ABD BDC ADB ∠-︒=∠2190,则AB 与CD BD +的大小关系如何?解答:延长CD 至E ,使BD DE =,连结AE .得到CD BD AB +=例14.(1999年天津市竞赛题)如图,△ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且AC BE =,延长BE 交AC 于F ,求证:EF AF =解答:延长ED 至H ,使DE DH =,连结CH .四、练习1.(第11届“希望杯”试题)若一个等腰三角形的三条边长均为整数,且周长为10,求底边的长. 解答:2或42.(2005年银川市中考题)如图,以直角三角形ABC 的两直角边BCAB ,为一条边,分别作等边△ABE 和等边△BCF ,连接EC EF ,.求证:(1)EC EF =;(2)CF EB ⊥. 解答:证明△EBF ≌△EBC3.(2001年柳州市中考题)如图,在等边△ABC 中,BE AD CD AE ,,=相交于P点,AD BQ ⊥于Q .求证:PQ BP 2=.解答:证明△ABE ≌△CAD4.(第11届“希望杯”试题)一个三角形的三条边的长分别是c b a c b a ,,(,,都是质数),且16=++c b a ,则这个三角形是( )A.直角三角形B.等腰三角形C.等边三角形D.直角三角形或等腰三角形解答:B5.(2002年江苏省初二第二试)如图,在△ABC 中,︒=∠=90,ACB BC AC ,D 是AC 上一点,BD AE ⊥于E ,BE 交AC 于D ,BD AE 21=,求证:BD 是ABC ∠的平分线.解答:延长BC AE ,相交于F .。
小学奥数《三角形的认识》教学课件

本讲主要内容: 三角形的定义; 三角形的分类; 三角形的三边关系; 三角形的内角和; 三角形的外角和。
新知探究
mathematics
知识梳理
数学知识点
mathematics
总一关:认识三角形 按边分类; 按角分类
新知探究
mathematics
第三关:多边形内(外)角和 每增加一条边,内角增加180度; 任意多边形外角和都是360度
1
2
3
1
3
2
其它多边形的内角和都 是通过三角形得到的
数学例题
mathematics
例题1: (1)三角形是由___________条边,___________个角,___________个顶点构成的; 下图 是一个三角形,如果用字母 A、B、C 分别表示三角形的三个顶点,那么这个三角形可以表 示为___________。 (2)三角形可以按照角来分: 三个角都是锐角的三角形叫做____________________; 有一个角是直角的三角形叫做____________________; 有一个角是钝角的三角形叫做____________________。 (3)三角形也可以按照边来分: 有两条边相等的三角形叫做____________________; 三条边都相等的三角形叫做____________________。
多边形内角和: 设边数为n,内角和为180°×(n-2)。 多边形外角和: 任意多边形外角和是360°。
2 1
1
3
2
4
1
3
2
数学例题
mathematics
例题3: (1)三角形三个内角的角度之和是多少度?你是怎么得到的呢? (2)如图 1,∠1+∠2+∠3+∠4=___________. (3)如图 2,∠1+∠2+∠3+∠4+∠5=____________. (4)如图 3,∠1+∠2+∠3+∠4+∠5+∠6=______________. (5)通过以上题目,总结: n边形的内角和=______________.
等腰三角形和等边三角形课件

02
等腰三角形的顶角记作$angle
A$,底角记作$angle
B$和
$angle C$。
性质
等腰三角形是轴对称 图形,有一条对称轴 ,即高线所在的直线 。
等腰三角形的三线合 一,即中线、垂线和 角平分线三线重合。
等腰三角形的两底角 相等,记作$angle B = angle C$。
等腰三角形的判定
巧。
中学数学竞赛
在中学数学竞赛中,等腰三角形和 等边三角形也是常见的考察内容, 旨在提高学生的数学素养和思维能 力。
大学生数学竞赛
在大学生数学竞赛中,等腰三角形 和等边三角形也经常出现,涉及的 知识点包括几何学、三角学和解析 几何等。
05
练习题与答案解析
基础练习题
题目1
一个等腰三角形的顶角是 70度,求它的底角?
等腰三角形和等 边三角形课件
汇报人: 202X-12-26
目录
• 等腰三角形的定义与性质 • 等边三角形的定义与性质 • 等腰三角形与等边三角形的异同
点 • 等腰三角形和等边三角形的实际
应用 • 练习题与答案解析
01
等腰三角形定义与性质
定义
01
等腰三角形是两边相等的三角形 ,记作$bigtriangleup ABC$, 其中$AB = AC$。
题目2
一个等腰三角形的底角是 45度,求它的顶角?
题目3
一个等腰三角形的两条腰 长为5厘米,求它的周长?
进阶练习题
题目4
一个等边三角形的边长为6厘米,求它的面积?
题目5
一个等边三角形的面积为15平方厘米,求它的边长?
题目6
一个等腰三角形的一个底角是60度,求它的顶角?
初中数学《等腰三角形》PPT执教课件 北师大版1

2. 如图,在△ABC 中,AC=BC,∠ACB=120°, CE⊥AB 于点 D,且 DE=DC.求证:△CEB 为 等边三角形.
证明:∵CE⊥AB于点D,且DE=DC, ∴BC=BE. ∵AC=BC,∠ACB=120°, CE⊥AB于点D, ∴∠ECB=60°. ∴△CEB为等边三角形.
初中数学《等腰三角形》PPT执教课件 北师大版1
初中数学《等腰三角形》PPT执教课件 北师大版1
初中数学《等腰三角形》PPT执教课件 北师大版1
在△ABE与△ADC中,
∴△ABE≌△ADC(SAS). ∴AB=AD. ∴AB=BD=AD,即△ABD是等边三角形.
初中数学《等腰三角形》PPT执教课件 北师大版1
初中数学《等腰三角形》PPT执教课件 北师大版1
角形.
初中数学《等腰三角形》PPT执教课件 北师大版1
(1)解:∵∠BAC=60°,∠C=70°, ∴∠ABC=180°-∠BAC-∠C =180°°-70°=50°. ∵BE 平分∠ABC, ∴∠FBD= ∠ABC=25°. ∵AD⊥BC,∴∠BDF=90°. ∴∠AFB=∠FBD+∠BDF=115°.
初中数学《等腰三角形》PPT执教课件 北师大版1
初中数学《等腰三角形》PPT执教课件 北师大版1
B
组
4. 如图,在△ABC 中,∠ABC=2∠C, BC=2AB=2BE,AD 是 BC 边的中线. 求证:△ABD 是等边三角形.
证明:∵BC=2AB=2BE,AD是BC边的中线, ∴AB=BD=CD=BE. ∴∠E=∠BAE. ∵∠ABC=∠E+∠BAE=2∠E,∠ABC=2∠C, ∴∠E=∠C. ∴AE=AC.
初中数学《等腰三角形》PPT执教课件 北师大版1
八年级奥数:等腰三角形的性质

八年级奥数:等腰三角形的性质等腰三角形的性质解读课标两边(角)相等的三角形是等腰三角形,等腰三角形是一类特殊三角形,具有以下丰富的性质:等腰三角形的两底角相等;等腰三角形是轴对称图形,底边上的高、中线、顶角的平分线互相重合;特别地,等边三角形的各边相等、各角都为60°.等腰三角形的性质为角度的计算、线段相等、直线位置关系的证明等问题提供了新的理论依据.熟悉以下基本图形、基本结论:问题解决例1 已知等腰三角形ABC 中,AB =AC ,D 为BC 边上一点,连结AD ,若△ACD 和△ABD 都是等腰三角形,则∠C 的度数是__________.例2 如图,在△ABC 中,D 在AC 上,E 在AB 上,且AB =AC .BC =BD ,AD =DE =BE ,则∠A 的度数为( ).A .30°B .45°C .60°D .75°例3 如图,在△ABC 中,已知∠A =90°,AB =AC ,D 为AC 中点,AE ⊥BD 于E ,延长AE 交BC 于F .求证: ∠ADB =∠CDF .例4 如图,在△ABC 中,AC =BC ,∠ACB =90°,D 是AC 上一点,AE ⊥BD 交BD 的延长线于E ,且AE =BD .求证:BD 是∠ABC 的角平分线. 12例5 操作:如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连结MN.数学冲浪知识技能广场1.等腰三角形的一个外角为100°,则这个等腰三角形的顶角的度数为_____________.2.如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C= _________.3.如图,AOB是一钢架,且∠AOB=10°,为使钢架更加坚固,需在其内部添加一些钢管EF、FG、GH ,添加的钢管长度都与OE相等,则最多能添加这样的钢管____根.4.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,那∠C的度数是______.5.如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小等于__________度.6.一如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是().A.①②③ 8.①②④ C.②③④ D.①③④7.如图,△ABC 中,AB =AC ,AE =AD ,∠BAD =,则∠EDC =( ).A .B .C .D . 8.在等腰△ABC 中,AB =AC ,一边上的中线BD 将这个三角形的周长分成15和12两个部分,则这个等腰三角形的底边长为( ).A .7 8.11 C .7或11 D .7或109.如图,在△ABC 中,∠ACB =90°,AC =AE ,BC =BF ,则∠ECF =( ).A .60.B .45.C .30.D .不确定10.如图,在△ABC 中,∠B =2∠C ,则AC 与2AB 之间的关系是( ).A .AC >2AB B .AC =2AB C .AC ≤2ABD .AC <2AB11.如图,在Rt △ABC 中,∠C =90°,AC =4,BC =3,以△ABC 的一边为边画等腰三角形,使它的第三个顶点在△ABC 的其他边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图中标明所画等腰三角形的腰长(不要求尺规作图).12.如图,在△ABC 中,AC =BC ,∠ACB =90°,将△ABC 绕点C 逆时针旋转角(0°<<90°),得到△A 1B 1C ,连结BB 1,设B 1C 交AB 于D ,A 1B 1分别交AB 、AC 于E 、F .(1)在图中不再添加任何线段的情况下,请你找出一对全等三角形,并加以证明(△ABC ≌△A 1B 1C 除外).(2)当△BB 1D 是等腰三角形时,求.13.已知Rt △ABC 中,AC =BC ,∠C =90°,D 为AB 边的中点,∠EDF =90°,将∠EDF 绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当∠EDF 绕D 点旋转到DE ⊥AC 于E 时(如图①),易证S △DEF +S △CEF =△ABC ,当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,S △DEF 、S △CEF 、S △ABC .又有怎样的数量关系?请写出你的猜想,不需证明. α12α13α14α23αααα12思想方法天地14.如图,在△ABC 中,AB =BC ,在BC 上取点M ,在MC 上取点N ,使MN =NA ,若∠BAM =∠NAC ,则∠MAC =_______________.15.有一个等腰三角形纸片,若能从一个底角的顶点出发,将其剪成两个等腰三角形纸片,则原等腰三角形纸片的顶角为____________度.16.已知△ABC 的某两个内角的比是4:7,且AB =AC ,BD ⊥AC 于D ,BE 平分∠ABC 交AC 于E ,则∠EBD 的大小是_____________. 117.如图,AA ’、BB ’分别是∠EAB 、∠DBC 的平分线,若AA ’=BB ’=AB ,则∠BAC 的度数为__________.18.在平面直角坐标系中,已知点A (3, 3),P 是y 轴上一点,则使△AOP 为等腰三角形的点P 共有( )个. .A .2B .3C .4D .519.如图,在△ABC 中,已知AC =BC ,∠ACB =90°,D 为AB 的中点,E 、F 分别为AC 、BC 上一点,且ED ⊥DF ,EM ⊥AB 于M ,FN ⊥AB 于N ,下列结论:①DE =DF ;②CE +CF =AC ;③S 四边形CEDF =S △ABC ;④EM +FN =AB .其中正确的有( ). A .① B .①② C .①②③ D .①②③④20.如图,在等腰Rt △ABC 中,AD 为斜边上的高,以D 为端点任作两条互相垂直的射线与两腰相交于E 、F ,连结EF 与AD 相交于G ,则∠AED 与∠AGF 的关系为( ).A .∠AED >∠AGFB .∠AED =∠AGFC .∠AED <∠AGF D .不能确定21.如图,已知四边形ABCD 中,AC 平分∠BAD ,DC =BC ,求∠ADC +∠ABC 的值.121222.如图,AE 、AD 是直线且AB =BC =CD =DE =EF =FG =GA ,若∠DAE =,求的值.应用探究乐园23.一个三角形可被剖分成两个等腰三角形,原三角形的一个内角为36°,求原三角形最大内角的所有可能值.24.已知点C 为线段AB 上一点,分别以AC 、BC 为边在线段同侧作△ACD 和△BCE ,且CA =CD ,CB =CE ,∠ACD =∠BCE ,直线AE 与BD 交于点F .(1)如图①,若∠ACD =60°,则∠AFB =____________;如图②,若∠ACD =90°,则∠AFB =___________;如图③,若∠ACD =120°,则∠AFB =____________;(2)如图④,若∠ACD =,则∠AFB =_______________(用含的式子表示);(3)将图④中的∠ACD 绕点C 顺时针旋转任意角度,如图⑤;试探究∠AFB 与的数量关系,并予以证明.ααααα。
等腰三角形和等边三角形的判定PPT课件
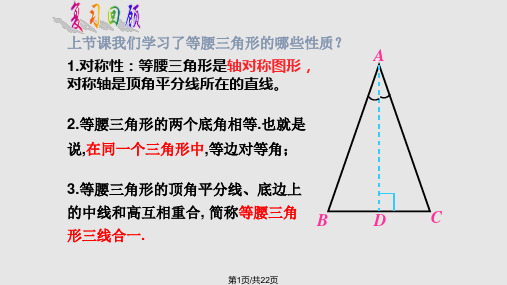
∴ ∠ADE=∠B,∠AED=∠C. (两直线平行,同位角相等)
∴ ∠ADE=∠AED(. 等量代换)
∴ △ADE为等腰三角形. (有两个角相等的三角形是等腰三角形)
第8页/共22页
动脑筋
有一个角是60°的等腰三角 形是等边三角形吗?为什么?
第9页/共22页
如图,在等腰三角形ABC中,
性质
判定
等
A 有两边 1.两腰相等
1.两边相等
腰
相等的
三
三角形 2.两底角相等 2.两角相等
角
是等腰
形 B
C 三角形 3. “三线合一”
4.是轴对称图形
第20页/共22页
等边三角形
名称 图 形 定 义
性质
判定
等
A 三边相 1.三边相等
1.三边相等
边
等的三
三
角形是 2.三角相等
2.三角相等
角 形B
等边三
由此得到等腰三角形的判定定理:
结论
有两个角相等的三角形是等腰三角形 (简称“等角对等边”).
注意:“等边对等角”的前提条件是在同一个三角形中。
A
几何语言表示如下:
在∆ABC中,
∵∠B=∠C
∴AB=AC
第5页/共22页
B
C
巩固练习:下列两个图形是否是等腰三角形?
300
400
400
750
第6页/共22页
结论
由此并且结合三角形内角和定理, 还可以得到等边三角形的判定定理: 三个角都是60°的三角形是等边三角 形。
第7页/共22页
例2 已知:如图,在△ABC中,AB=AC,点D, E分别是AB,AC上的点,且DE∥BC.
专题27 等腰三角形与等边三角形(教师版)

一、选择题 9.(2020·绍兴)如图,等腰直角三角形ABC 中,∠ABC =90°,BA =BC ,将BC 绕点B 顺时针旋转θ(0°<θ<90°),得到BP ,连结CP ,过点A 作AH ⊥CP 交CP 的延长线于点H ,连结AP ,则∠P AH 的度数( )A .随着θ的增大而增大B .随着θ的增大而减小C .不变D .随着θ的增大,先增大后减小 {答案}C{解析}本题考查了等腰三角形的性质,三角形的内角和,旋转的性质.由旋转得BC=BP=BA ,∴△BCP 和△ABP 均是等腰三角形.在△BCP 中,∠CBP=θ,BC=BP ,∴∠BPC=90°-12θ.在△ABP 中,∠ABP=90°-θ,同理得∠APB=45°+12θ,∴∠APC=∠BPC +∠APB =135°,又∵∠AHC=90°,∴∠PAH=45°,即其度数是个定值,不变.因此本题选C .7.(2020·铜仁)已知等边三角形一边上的高为2,则它的边长为( ) A .2 B .3 C .4 D .4{答案}C {解析}设等边三角形的边长为2x ,过等边三角形的一个顶点作对边的高,由等边三角形“三线合一”的性质得直角三角形的一条直角边为x ,由勾股定理得x2+(2)2=(2x )2,解得x=4,因此本题选C .3.(2020·聊城)如图,在△ABC 中,AB =AC ,∠C =65°,点D 是BC 边上任意一点,过点D 作DF ∥AB 交AC 于点E ,则∠FEC 的度数是( )A .120°B .130°C .145°D .150°{答案}B{解析}可利用三角形的外角性质求∠ FEC 的度数,结合等腰三角形与平行线的性质,可得∠ EDC 、∠B 均与∠C 相等.即:∵AB =AC ,∴∠B =∠C =65°.∵DF ∥AB ,∴∠ EDC =∠B =65°.∴∠FEC =∠EDC +∠C =65°+65°=130°.10.(2020·河南)如图,在△ABC 中,AB =BC =3,∠BAC =30°,分别以点A ,C 为圆心,AC 的长为半径作弧,两弧交于点D ,连接DA ,DC ,则四边形ABCD 的面积为( ) A.63 B.9 C.6 D. 33{答案}D{解析}∵分别以点A 、C 为圆心,AC 的长为半径作弧,两弧交于点D , ∴AD=AC=CD ,∴△ACD 是等边三角形,∴∠DAC=60°.∵AB=BC ,AD=CD ,连接BD 交AC 于点E ,∴BD 垂直平分AC ,∴∠AEB=90°.ABCD E F在Rt △ADE 中,∵∠DAC=60°,∠AED=90°,AE=32,∴323∴四边形ABCD 的面积为:3333221=⨯⨯.9.(2020自贡)如图,在Rt△ABC 中,△ACB =90°,△A =50°,以点B 为圆心,BC 长为半径画弧,交AB 于点D ,连接CD ,则△ACD 的度数是( )A .50°B .40°C .30°D .20°{答案} D .{解析}本题考查了直角三角形,圆,等腰三角形等知识,∵在Rt △ABC 中,∠ACB =90°,∠A =50°,∴∠B =40°,∵BC =BD ,∴∠BCD =∠BDC =12(180°﹣40°)=70°,∴∠ACD =90°﹣70°=20°,因此本题选D .5.(2020·福建)如图,AD 是等腰三角形ABC 的顶角平分线,5=BD ,则CD 等于( )A.10B.5C.4D.3{答案}B{解析}本题考查了等腰三角形三线合一的性质,∵AD 是等腰三角形ABC 的顶角平分线,5=BD,∴CD=BD=5,因此本题选B .(2020·南充) 6.如图,在等腰三角形ABC 中,BD 为∠ABC 的平分线,∠A=36°,AB=AC=a ,BC=b ,则CD=( )(第6题) A.2b a + B.2ba - C.a-b D.b-a {答案}C{解析}∵AB=AC ,∠A=36°,∴∠ABC=∠ACB=72°,∵BD 平分∠ABC ,∴∠ABD=12∠ABC=12×72°=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠C=∠BDC=36°,∴BD=BC=b ,同理:AD=BD=b ,∴CD=AC-AD=a-b ,故选C .(2020·济宁)5.一条船从海岛A 出发,以15海里/时的速度向正北航行,2小时后到达海岛B 处.灯塔C 在海岛在海岛A 的北偏西42°方向上,在海岛B 的北偏西84°方向上.则海岛B 到灯塔C 的距离是()A.15海里B.20海里C. 30海里D.60海里 {答案}C{解析}根据题意画图,如图,∠A=42°,∠DBC=84°,AB=15×2=30(海里), ∴∠C=∠DBC-∠A=42°,∴BC=BA=30(海里).10.(2020·无锡)如图,等边△ABC 的边长为3,点D 在边AC 上,AD =12,线段PQ 在边BA 上运动,PQ=12,有下列结论:NMHG AB CD EFC B FE ABC P QDD Q C B(P)AE①CP 与QD 可能相等; ②△AQD 与△BCP 可能相似; ③四边形PCDQ 面积的最大值为31316; ④四边形PCDQ 周长的最小值为3+372.其中,正确结论的序号为( )A .①④B .②④C .①③D .②③{答案} D{解析}设AQ =x ,则BP =52—x①如图1,当点P 与B 重合时,此时QD 为最大,过点Q 作QE ⊥AC ,∵AQ =52,∴AE =54,QE =534,∴DE =34,∴此时QD =212,即0≤QD ≤212;而332≤CP ≤3,两个范围没有交集,即不可能相等;①错误②若△AQD ∽△BCP ,则AD BP =AQ BC ,代入得2x 2—5x +3=0,解得x 1=1,x 2=32,∴都存在,∴②正确;③如图2,过点D 作DE ⊥AB ,过点P 作PF ⊥BC ,S 四边形PCDQ =S △ABC —S △AQD —S △BPC =34×32-12⋅x ⋅34-12×3×34(52-x )=34 x +21316,∵52—x ≥0,即x ≤52,∴当x =52时面积最大为31316;③正确; ④如图,将D 沿AB 方向平移12个单位得到E ,连接PE ,即四边形PQDE 为平行四边形,∴QD =PE ,四边形周长为PQ +QD +CD +CP =3+PE +PC ,即求PE +PC 的最小值,作点E 关于AB 的对称点F ,连接CF ,线段CF 的长即为PE +PC 的最小值;过点D 作DG ⊥AB ,∴AG =14,EN =FN =HM =34,∴CH =332+34=734,FH =MN =32-14-12=34,∴FC =392,∴四边形PCDQ 周长的最小值为3+392,④错误.DQ PCB A13.(2020·湖北孝感)某型号飞机的机翼形状如图所示,根据图中数据计算AB的长为________米.(结果保留根号)(第13题){答案}(533-1.6).{解析}如图,过点A作AM⊥CM于M,则CM=5m,在Rt△BCM中,∠BCM=30°,所以BM=CM∙tan30°=53.由题意可知△DCN是等腰直角三角形,所以CN=CD=3.4m,所以MN=5-3.4=1.6(m),因为△AMN是等腰直角三角形,所以MN=AM=1.6m,所以AB=BM-AM=(533-1.6)m.故答案为(533-1.6).第13题答图6.(2020·荆门)如图3,△ABC中,AB=AC,∠BAC=120°,BC=23,D为BC的中点,AE=14AB,则△EBD的面积为( )A.334B.338C.34D.38{答案}BDECAB图3{解析}连结AD .∠B =∠C =12×(180°-∠A )=30°.由等腰三角形的“三线合一”可知AD ⊥BC .∴AD=BD ·tan B =1.∴S △ABC =12BC ·AD =12××1AE =14AB ,∴S △EBD =34S △ABD=38S △ABC .故选B .7. (2020·张家界)已知等腰三角形的两边长分别是一元二次方程2680x x -+=的两根,则该等腰三角形的底边长为( ) A. 2 B. 4C. 8D. 2或4{答案}A{解析}本题考查了等腰三角形的性质,三角形的三边关系,解一元二次方程,能求出方程的解并能够判断三角形三边存在的条件是解此题的关键.解一元二次方程求出方程的解,得出三角形的边长,用三角形存在的条件分类讨论边长,即可得出答案. 解:x 2-6x+8=0 (x -4)(x -2)=0 解得:x=4或x=2,当等腰三角形的三边为2,2,4时,不符合三角形三边关系定理,此时不能组成三角形; 当等腰三角形的三边为2,4,4时,符合三角形三边关系定理,此时能组成三角形, 所以三角形的底边长为2, 故选:A .14.(2020·青海)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( ) A .55°,55° B .70°,40°或70°,55° C .70°,40° D .55°,55°或70°,40° {答案}D{解析}(1)当70°是顶角时,另两个角相等,都等于12×(180°-70°)=55°;(2)当70°是底角时,另一个底角也是70°,顶角=180°-70°×2=40°.因此另外两个内角的底数分别是55°,55°或70°,40°.故选D . 5.(2020·临沂)如图,在ABC ∆中,AB AC =,40A ∠=︒,//CD AB ,则BCD ∠=( )A.40°B.50°C.60°.D.70°{答案}D{解析} 根据三角形内角和定理和等腰三角形的等边对等角且AB AC =,40A ∠=,可得:70ABC ACB ∠=∠=;然后根据两直线平行内错角相等且//CD AB 可得:70BCD ABC ∠=∠=,所以选D . 11.(2020·宜宾)如图,△ABC 和△ECD 都是等边三角形,且点B 、C 、D 在一条直线上,连结BE 、AD ,点M 、N 分别是线段BE 、AD 上的两点,且BM =13BE ,AN =13AD ,则△CMN 的形状是( )A .等腰三角形B .直角三角形C .等边三角形D .不等边三角形{答案} C{解析} 由△ABC 和△ECD 都是等边三角形,可得△BCE ≌△ACD (SAS ),∴∠MBC =∠NAC ,BE =AD ,∵BM =13BE ,AN =13AD ,∴BM =AN ,∴△MBC ≌△NAC (SAS ),∴MC =NC ,∠BCM =∠ACN ,∵∠BCM+∠MCA =60°,∴∠NCA+∠MCA =60°,∴∠MCN =60°,∴△MCN 是等边三角形.9.(2020·玉林)如图,A ,B ,C 三岛的平面图,C 岛在A 岛的北偏东35°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西55°方向,则A ,B ,C 三岛组成一个( )A .等腰直角三角形B .等腰三角形C .直角三角形D .等边三角形 {答案}A{解析}如图所示: ∵C 岛在A 岛的北偏东35°方向,∴∠CAD =35°,∵B 岛在A 岛的北偏东80°方向,∴∠BAD =80°,∴∠CAB =∠BAD -∠CAD =45°, ∵C 岛在B 岛北偏西55°方向,∴∠CBE =55°, 又∵DA ∥EB ,∴∠ABE+∠BAD=180°,∴∠ABE=100°,∵∠CBE=55°,∴∠CBA=100°-55°=45°,∴∠CBA=∠CAB,∴CA=CB,在△ABC中,∴∠C=180°-∠ABC-∠CAB=180°-45°-45°=90°,∴△ABC为等腰直角三角形,故选:C.9.(2020·毕节)已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为()A.13 B.17 C.13或17 D.13或10{答案}B,{解析}本题考查等腰三角形的三边关系.解:分两种情况讨论:若3为底边,腰长为7,则此等腰三角形的周长为3+7+7=17;若7为底边,腰长为3,则此等腰三角形不存在,因为3+3<7,不符合三角形的三边关系,故选B.9.(2020·烟台)七巧板是我们祖先的一项创造,被誉为“东方魔板”.在一次数学活动课上,小明用边长为4cm的正方形纸片制作了如图所示的七巧板,并设计了下列四幅作品﹣﹣“奔跑者”,其中阴影部分的面积为5cm2的是()A.B.C.D.【解析】最小的等腰直角三角形的面积=18×12×42=1(cm2),平行四边形面积为2cm2,中等的等腰直角三角形的面积为2cm2,最大的等腰直角三角形的面积为4cm2,则A、阴影部分的面积为2+2=4(cm2),不符合题意;B、阴影部分的面积为1+2=3(cm2),不符合题意;C、阴影部分的面积为4+2=6(cm2),不符合题意;D、阴影部分的面积为4+1=5(cm2),符合题意.故选:D.10.(2020·天门仙桃潜江)如图,已知△ABC和△ADE都是等腰三角形,△BAC=△DAE=90°,BD,CE 交于点F,连接AF.下列结论:△BD=CE;△BF△CF;△AF平分△CAD;△△AFE=45°.其中正确结论的个数有A.1 B.2个C.3个D.4个{答案}C{解析}∵△ABC 和△ADE 都是等腰直角三角形, ∴AB=AC ,AD=AE , ∵∠BAD=90°+∠CAD , ∠CAE=90°+∠CAD , ∴∠BAD=∠CAE , 在△AEC 与△ADB 中,AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩, ∴△AEC ≌△ADB(SAS), ∴BD=CE ,故①正确; ∴∠ADB=∠AEC ,∵∠DEF+∠AEC+∠EDA=90°, ∴∠DEF+∠ADB+∠EDA=90° ∴∠DEF+∠EDF=90∘, ∴BD ⊥CE ,故②正确; ∵作AN ⊥CE ,AM ⊥BD ∵△AEC ≌△ADB(SAS), ∴AM=AN ,∵AF 是∠BFE 的角平分线, ∠BFE=90°,∴∠AFE=45°,故④正确 ,故③正确;因为QF ≠PF ,故③错误。
等腰三角形和等边三角形(整理)PPT课件

说一说 填一填
3. ( 两条边相等 )的三角形是等腰三角形,
两个底角(相等)。
(
)的三角形是等边三角形,每个
角都是( )度,它又是一个
(
)。
说一说 填一填
3. ( 两条边相等 )的三角形是等腰三角形, 两个底角(相等)。
(三条边都相等)的三角形是等边三角形, 每个角都是( 60 )度,它又是一个( 锐 角三角形 )。
说一说 填一填
• 1. ( 由三条线段围成 )的图形叫做三 角形,三角形具有( 稳定 )性。三角 形有( 3 )个顶点,( 3 )条边, ( 3 )个角,( )条高。
说一说 填一填
• 1. ( 由三条线段围成 )的图形叫做三 角形,三角形具有( 稳定 )性。三角 形有( 3 )个顶点,( 3 )条边, ( 3 )个角,( 3 )条高。
条路最近?途中那两条路一样长?为什么?
40米
20米
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
43
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
说一说 填一填
• 4.(1)一个三角形的内角和是(180)度。 • (2)用两块完全一样的三角形拼成一
个三角形,这个三角形的内角和是(180) 度。 • (3)把一个大三角形剪成两个小三角 形,每个小三角形的内角和是(180)度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十讲等腰三角形和等边三角形基础知识b等腰三角形的性质及推论:(1)等腰三角形的两底角相等(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(三线合一)(3)等边三角形的各角都相等,并且每一个角都等于60。
2.等腰三角形的判定及推论:(1)从定义入手,证明一个三角形的两条边相等(2)从角入手,证明一个三角形的两个角相等(3)有一个角为60。
的等腰三角形是等边三角形尤其要注意全等在等腰.等边三角形中的应用.二.名校真题回放1.(北京市西城区2006年抽样测试八年级(上)试卷)如图,在'ABC中,4B = AC, 它的周长为24,又AD丄BC于D, AABD的周长为20,则AD的长为多少?解答:82.(北京市西城区2006年抽样测试八年级(上)试卷)在等边三角形ABC中,D卫分别在边BCAC上, DC = AE, AD、BE交于点F •请你判断ZDACfUZABE的大小关系,并证明你的结论.解答:ZDAC = ZABE3.(北京市西城区2006年抽样测试八年级(上)试卷)已知:如图'△ABC中,AB=AC,D为AC上一点,ZDBC = -ZA•求证J AC丄BD 2解答:利用三角形内角和•4.(北京市西城区2006年抽样测试八年级(上)试卷)已知△ ABC的三边4人C满足等式:“2+2ah-2be = O,试说明△ ABC是等腰三角形.解答5 (“ 一c)(« + C + 2h) = 05.(2006年海淀区八年级第一学期期末测评)如图为一张梯形纸片ABCD,AD//BC, ZBDC = 90。
.将其沿对角线BD翻折后压平, 仙和BC'相交于点E,则图中的等腰三角形有__________________ , _________________ (只写出两个正确结论)解答:“BED,△〃(:(?等等.三、活题巧解(一)等腰三角形的性质例1.(竞赛选题)在A ABC 中,AB M AC, ZA=100° , BD 为ZB 的平分线,求证:BC=BD+ADo 证明:在BC 上截取BE=BD,截取BF=BA,连接DE, DFVAB=AC, ZA=100"八••ZC=40° . ZDBC=20° A ZDEB=80"/. ZCDE=ZDEB-ZC=8O** -40° =40° ・•. ZCDE= ZC, :、DE=EC ①XVAB=BF, ZABI>=ZFBD, BD=BD, A A ABD$^ A FBD ADA=DF ② 又VZDFC=180" -ZDFB=180" -ZA=80° , :.乙DEB=:ZDFC=8O" , ADE=OF ③ 由①©③的EC=AD /.BC=BE+EC=BD+AD例2. (2002年上海市竞赛题)如图,AC.BD 相交于AC 平分ZDAB.且AB = AE.AD = AC.有以下四个结论:(1) &C 丄BD : (2) BC=DE : (3) ZD 心『DAB ;⑷"亚是等边三角形•其中正确的结论是什么?(2) (3)等腰 A ABC 中,AB 二AC, ZA=20。
. D 是 AB 边上一点,AB=BC,连接 6 ZBDC=3O" i^AAED^ ABAC,连接 EC,贝!|ZAED=ZBAC 20", ZDAE=ZADE=ZB=ZACB=8(rAZCAE=ZDAE-ZBAC=80° -20" =60° 又 VAE=AB=ACA A ACE 是一个多边三角形,有AE 二EC=ED A ZDEC=ZAEC-ZAED=40°AZEDC=- (180" -40° ) =70"2AZBDC=180" - (ZADE+ZEDC) =30°例4.(第11届“希望杯”试题)如图,在△ ABC 中,AC = 2,SC = 4,ZACB = 60% 将△4BC 折叠,使得点B 和点C重合,折痕为DE,则△AEC 的面积是多少? 解答5 —Vs3解答: 例3 求证: 证明:F EDCBAADDB例5 (竞赛选题)A ABC 是等腰直角三角形,ZBAC=90* ,点D 是AABC 内一点,且ZDAC= ZDCA=150" 求证:BD 二BA 证明:以AD 为边在AADB 由作等边AAOE,连接BE,则Z1=Z2=Z3=6(r , AE=ED 二AD VZDAC=15O",A ZEAB=90" ・Z1・ZDAC=15O° . A ZDAC=ZEAB XVDA=AE, AB=ACA A EAB 丝 A DAG A ZEBA=ZDCA=150" ••■ZBEA=180" -ZEBA ・ZEAB=150° ZBED=360。
-ZBEA-ZAED=150" A ZBEA=ZBED 又 TBE=BE, AE=ED A A BEA 丝 A BED ABD^BA例6・(1997年天津市竞赛题)如图,△ABC 是边长为1的等边三角形,ZBDC = 120°、BD = CD,点 M,N 分别在 AB/C 上,且ZMDN = 60。
,连结MV,求证:△AMN 的周长等于2.解答:延长/1<?至£,快CE = BM,连结DE •先证△ BMD 辿 CED.再证△ MDN 空△EDN.例7. (2000年无锡市竞赛题)在△ABC 中,AB = AC.过△ABC 某一顶点的直线可将△ ABC 分成 两个等腰三角形,试求△ABC 各内角的度数.解答,共有4种情况,其内角相应度数为:183 540° 540。
(450,45^900),(36^36M08«),(36Vr,7r),(— — —A例8. (2002年泰州市中考题)如图,在△ABC 中,AB = AC. ZA = 36% BD 、CE B C解答:8个(二)等腰三角形的判定分别为厶〃GZACB 的角平分线,且相交于F,则图中的等腰三角形有几个?例9.(第64届莫斯科数学竞赛题〉如图,在AABC 中,作出它的角平分线AK,中线BL 和高CM* 是缚边三角形证明:YA AMC 是直角三角形,L 是斜边AC 中的中点。
AAL=LC=ML 又 ML=LK=MK AAL=LC=LKA A ACK 也是直角三角形 •••AK 丄 BC・:AK 既是A ABC 的角平分线,又是它的高。
A AABC 是等腰三角形t AAB=AC又在RtABMC 中,K 是BC 中点,ABC=2MK=2KL=AC AAB=BC=AC•••A ABC 为等边三角形例10.(1999年江苏省竞赛题)已知△4BC 是等边三角形,£是4C 延长线上的任意一点,△(:£>£:也是等边三角形,若M.N 分别畏线 段AD.BE 的中点,求证:ZiCMN 是等边三角形. 解答:先证4ACD 沁 BCE.再证△DCM 丝△ECN,得到CM =CN 上 NCM =60°例H- (1996年北京市竞赛题)三角形三边长“上,C 满足一・- + - =—-—,则三角形一定是() a b C“一o+c解答:把原式恒等变形,得到(b-c )(a-b )(a+c ) = Q.故选D.例12.(第3届“希望杯”试题)等腰三角形的周长为《 , 一腰的中线将周长分成5:3的两部分,则此三 角形的底边长是多少?A一点,ZABD = 60。
,ZADB = 90。
-二 ZBDC ,则 AB 与 BD + CD 的大小关系如/ \ \«uVB C如果A KLM 是等边三角形,证明:A ABC 也A.等边三角形C •以C 为底边的尊腰三角形B.以《为底边的等腰三角形D.等腰三角形 解答:分情况讨论,两种情况里舍去一种,解得底边长为-“6例13・(2001年唐山市中考题)如图,在△ABC 中,AB = AC. D 为△ABC 外 何?解答:延长仞至£,使DE = BD ・连结•得到AB^BD + CDL例14・(1999年天津市竞赛题)如图,△4BC中,AD是BC边上的中线,E是仙上的一点,且BE = AC,延长BE交AQ于F, 求证:AF=EF解答:延长ED至使DH = DE・连结CH.例15.(第11届初二培训)如图,已知等边三角形AABC内有一点N, ND丄BC, NE丄AB, NF丄AC, D, E, F 都是重足,M是A ABC中异于N的另一点,若Pi=ND+NE=NF. P2=MD=ME=MF.即Pi与P2的大小关系是,解:如图,连结AN, BN, CN 69 A ABN, ABCN, AACN,则S A ABC=S & ABX+S A BCN+S A ACN设A ABC的边长AB=BC=CA=a,高为h则-ah= -a*NE+-a •ND+-a*NF=>ND+NE+NF=h2 2 2 2同理• LLM作MD丄BG MF丄AC, ME'丄AB可得s MA +ME' +MF* =h又MDMMD,, MEMME,■ MF>MF* ,且其中至少有一个式子的等号不成立.A P I=ND+NE=NF<MD+ME+MF=P2四、练习1.(第10届初二希望杯试题)如图,C是线段AB上,在AB 的同侧作等边三角形△ ACM和ABCN,连结AN, BM.若Z MBN=38。
,则ZANB=_。
解:由△ ACM与△ BCN均为等边三角形,知AM=CM=AC,CN=BN=BC,在AACN与AMCB 中,AC二MC, CN=CB, ZCANMCT +ZMCN=Z MCB所以△ ACN^AMCB, ZANC= ZMBG因为ZMBNM8° ,所以ZMBC=60。
・38° =22° , ZANB=ZANC+ZCNB=82"2. (2005年银川市中考题)如图,以直角三角形ABC的两宜角边AB.BC为一条边,分别作等边△ABE和等边△BCF,连接EF,EC•求证.(1)EF = E6 (2) EB丄 CF. 解答:证明△ EBF辿 EBC3. (2001年柳州市中考题)如图,在等边△ABC中,AE = CD.AD.BE相交于P 点,Bg丄AD于Q.求证:BP = 2PQ.解答:证明'ABEg'CAD NMB CACFAEQD CA4. (1998年南宁市竞赛题)如图,正三角形ABC中,分别是AB.AC.BC的中点,M为RC上任意一点,ZXMSP为正三角形•求证:RM = QS・解答:连接P&PR5. (2001年沈阳市中考题)如图,ABCD是平行四边形,以AC为边长在两侧各作一个正三角形ACP.ACQ.求证:BPDQ为平行四边形.解答:\ADQ 沁 CBP、故DQ = BP,同理,BQ=DP6.(第7届初二第2试)如图,P是尊边AABC中的-4'^,PA=2.PB=2A/3,PC=4,则A ABC的边长是.C 解:如图,将A BAP绕B点逆时针旋转60° ,则BA与BC重合,BP移到Bld处,PA 移到MC 处,所以BM=BP> MC=PA, ZPBM-60"。
