圆弧法边坡稳定性分析计算表格
圆弧法计算滑坡稳定系数
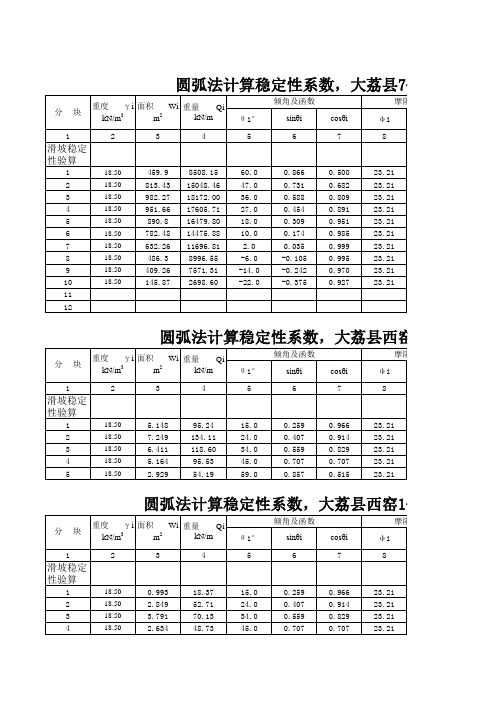
3
4
5
6
7
459.9 813.43 982.27 951.66 890.8 782.48 632.26 486.3 409.26 145.87
8508.15 15048.46 18172.00 17605.71 16479.80 14475.88 11696.81 8996.55 7571.31 2698.60
701.5
2513.7 14256.0 6814.6
1.33
0.429
50
13.68
684
408.2 11689.7 5696.6
0.429
50
13.62
681
-940.4 8947.3 4517.7
0.429
50
13.79
689.5 -1831.7 7346.4 3839.7
0.429
50
14.35
717.5 -1010.9 2502.1 1790.4
荔县西窑1---1'治理工程剖面稳定性验算表
摩阻力 tyφi 9
ci
粘阻力 li
ci·li kN/m
滑动分力Ti 法向分力Ni
kN/m
kN/m
11
12
13
19
20
抗滑力 Ri
kN/m 21
稳定系数 Fs
24
0.429
26
0.429
26
0.429
26
3
4
5
6
7
96.84 171.55 211.59 237.48 209.28 178.22 151.45 119.54 69.43 15.48
1791.54 3173.68 3914.42 4393.38 3871.68 3297.07 2801.83 2211.49 1284.46 286.38
边坡稳定分析
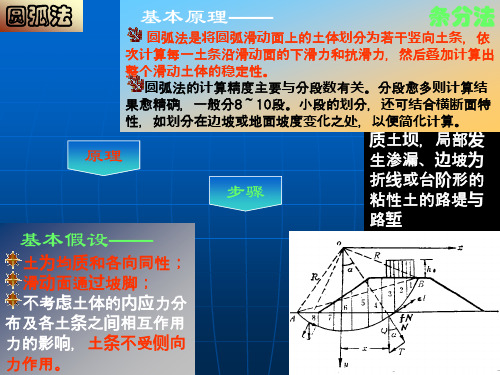
NQ BL
2 800 1.88m 6.4 7.4 18
13 arctg 2518n 27.5
解: (3)按4.5H法确定滑 动圆心辅助线。在此取 θ=25°,由表4-1得β1 =25°,β2=35°。据此 两角分别自坡脚和左顶 点作直线相交于O点, BO的延长线即为滑动 圆心辅助线。 (4)绘出三条不同位置 的滑动曲线: ①一条通过路基中线; ②一条通过路基的右 边缘(如图中的圆弧所 示); ③一条通过距右边缘 1/4路基宽度处。
解: (10)将每一段的重力 Gi化为二个分力: a.在滑动曲线法线 方向分力:Ni=Gicosαi b.在滑动曲线切线 方向分力:Ti=Gisinαi 并分别求出此两者之 和,ΣNi和ΣTi (11)算出滑动曲线圆 弧长L (12)计算稳定系数
圆弧法边坡稳定性分析表
分 段 1 sinα 0.85 α 58°00′ cosα 0.53 Ω m2 29.9 G=Ω KN 508 Ni=Gicosαi KN 269 Ni=Gisinαi KN 732 L m
步骤
计算每一小段滑动面上的 反力(抵抗力),即内摩擦力 Nif(其中f=tgi )和粘聚力cLi (Li为i小段弧长)。
以圆心O为转动圆心,半径R 为力臂,计算滑动面上各力对O 点的滑动力矩和抗滑力矩。
抗滑力矩
n n M r R N i f cLi i 1 i 1
2
3 4 5 6 7 8
0.64
0.47 0.28 0.11 -0.07 -0.27 -0.37
39°47′
28°02′ 16°15′ 6°18′ -4°00′ -15°40′ -21°43′
0.77
0.88 0.96 0.99 0.99 0.97 0.93
土坡圆弧滑动按整体稳定法

mαi值曲线
例6-3 用简化的毕肖普法计算例题6-2土坡 的稳定安全系数。
土
条
编 号
i ()
lii
(m)
1 6.08 1.30
2 12.64 1.31
3 19.38 1.37
4 26.41 1.41
5 33.90 1.54
6 42.13 1.75
7 51.61 2.04
8 63.73 3.12
合 计
26.11 33.63 41.15 47.66 54.88 60.17 55.68 52.29
26.08 33.60 41.03 47.52 54.65 59.77 55.26 51.72
319.47
371.57 369.63
第一次试算后,求得稳定安全系数:
泰勒确定最危险滑动面圆心的经验方法
当 0且 53时,滑动面可能是中点圆,
也有可能是坡脚圆或坡面圆,它取决于硬层
的埋藏深度。当土体高度为H,硬层的埋藏深
度为ndH。若硬层埋藏较深,则滑动面为中点 圆,圆弧滑动面与硬层相切,滑动面与土面 的交点为A,A点距坡脚的躏为nxH,nx可根据 nd及β值查表得,若硬层埋藏较浅,则滑动面 可能是坡脚圆或坡面圆,其圆心位置需通过 试算确定。
n
的 作 用
i
Ti
K Mr
R (Wi cosi
i1
tani
cili
)
Ms
n
R Wi sini
i1
力
Ni li
n
K Mr
tan Wi cosi
i1
cL
Ms
n
Wi sini
i1
n
K Mr Ms
tan Wi cosi
边坡稳定性计算表
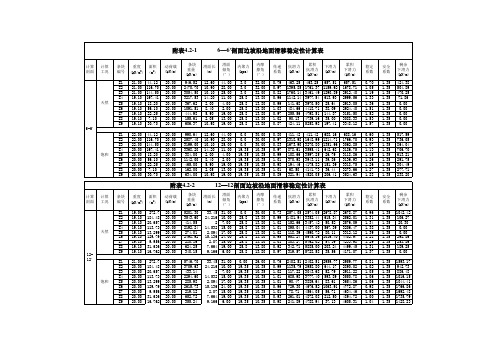
E9 19.10 16.762 20.00 340.15 9.166 6.00 25.8 13.80 0.97 319.57 5728.58 35.56 4171.07
E1 21.00 272.7 20.00 5746.70 33.45 31.00 0.00 26.00 0.76 2402.51 2402.51 2959.77 2959.77
内聚力 (kpa)
3.0 3.0 3.0 25.8 25.8 25.8 25.8 25.8 25.8
内摩 擦角 (°)
32.00 32.00 32.00 13.80 13.80 13.80 13.80 13.80 13.80
传递 系数
0.79 0.97 0.82 0.96 0.99 1.03 0.97 1.02 0.87
E2 20.00 184.48 20.00 3709.63 24.216 10.00 19.35 10.35 0.99 1135.79 2958.80 644.17 2890.02
E3 20.00 20.657 20.00 433.14
2 7.00 19.35 10.35 1.02 117.22 3043.68 52.79 2911.22
安全 系数
1.35 1.35 1.35 1.35 1.35 1.35 1.35 1.35 1.35
剩余 下滑力 (kN/m)
424.38 504.89 470.25 71.86
0.00 0.00 0.00 0.00 0.00
1.35 1.35 1.35 1.35 1.35 1.35 1.35 1.35 1.35
E1 19.00 272.7 20.00 5201.30 33.45 31.00 0.0 30.00 0.73 2574.05 2574.05 2678.87 2678.87
基于Bishop方法的EXCEL计算边坡稳定性计算
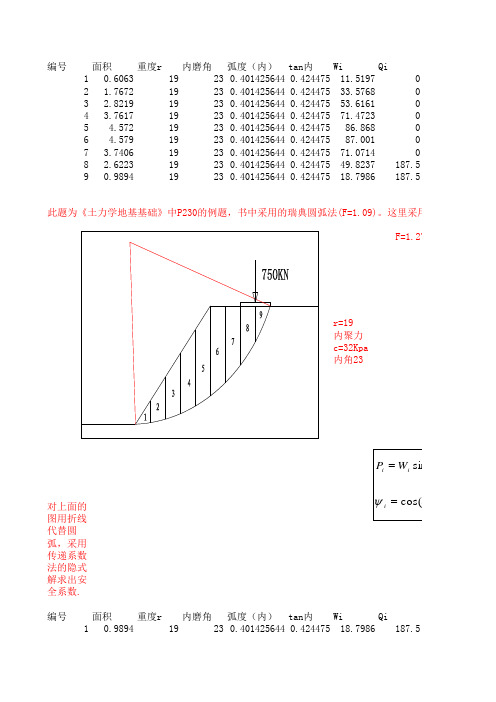
6 3.7617
19
23 0.401425644 0.424475 71.4723
7 2.8219
19
23 0.401425644 0.424475 53.6161
8 1.7672
19
23 0.401425644 0.424475 33.5768
9 0.6063
19
23 0.401425644 0.424475 11.5197
0.985919 60.73016 45.78545 1.240837 0.985221 60.77319 45.78545 1.241563 0.985092
0.942883 140.6092 170.2456 1.240837 0.942105 140.7253 170.2456 1.241563 0.941962
0
8 2.6223
19
23 0.401425644 0.424475 49.8237 187.5
9 0.9894
19
23 0.401425644 0.424475 18.7986 187.5
此题为《土力学地基基础》中P230的例题,书中采用的瑞典圆弧法(F=1.09)。这里采用简化Bishop法. F=1.279
1.05675 47.94511 15.84464 1.240837 1.05643 47.95964 15.84464 1.241563 1.056371
1.054698 54.40672 27.83262 1.240837 1.054276 54.42849 27.83262 1.241563 1.054198
ma
抗滑动力 下滑力 F
ma
抗滑动力 下滑力 F
ma
路基边坡稳定性验算

路基边坡稳定性验算计算书
一、计算说明
本设计路线中,以K0+080断面路堑边坡高度(H=30m)最高,故本计算算例取K0+080断面边坡进行计算。
具体边坡稳定性分析参数:路基填土为低液限粘土,粘聚力c=10Kpa,内摩擦角27度。
容重r=17KN/m3,荷载为公路Ⅰ级。
计算方法采用4.5H法确定圆心辅助线。
此边坡坡率不一致,故采用平均坡度进行计算,经计算可知此边坡的平均坡度为1:1.如下图示:
二、计算过程分析
计算原理采用瑞典条分法,将圆弧滑动面上的土体按照6m的宽度进行划分。
下图所示为o1圆弧滑动面的计算实例
采用计算表格可得计算结果:
L=
=R θπ
180
88.02m 则边坡稳定系数为: =
+=
∑∑i
hi b i
hi b cL Ks θγθϕγsin cos tan =⨯⨯⨯⨯⨯+⨯505
.9661701
.23927tan 61702.8810 1.35>1.25
按照上述方法一一计算出o2、o3、o4、o5处的稳定系数分别为1.32、1.29、1.33、1.37.故取Ks=1.29为最小的稳定系数,此时由于Ks>1.25,所以边坡稳定性满足要求。
边坡稳定性计算表
336.37 336.37 748.48 1084.85 1704.90 2789.75
下滑力 (kN/m)
412.76 799.22 1661.11
457.51 860.03 1788.26
累积 下滑力 (kN/m)
412.76 1211.98 2873.09
457.51 1317.54 3105.80
3.45 3.94 1.18
26.00 28.00 32.00
26.00 28.00 32.00
0.0 0.0 0.0
0.00 0.00 0.00
30.00 30.00 30.00
36.10 101.30 47.42
36.10 137.39 184.82
25.00 25.00 25.00
30.14 85.32 39.75
附表4.1.2-1
3─3'剖面边坡沿地面滑移稳定性计算表
计算 计算 剖面 工况
条块 重度 面积 编号 (kN/m3) (m2)
动荷载 (kN/m)
条块 重量 (kN/m)
滑面长 (m)
3-3'
自重+动 荷载
自重+动 荷载+暴
雨
条块1 条块2 条块3
条块1 条块2 条块3
18.90 19.50 19.50
荷载+暴 E2
雨
E3
21.00 21.00 21.00
22.00 22. 3.66
20.00 20.00 20.00
69.56 198.71 96.86
3.45 3.94 1.18
20.00 20.00 20.00
71.92 207.22 100.52
边坡稳定性分析例题
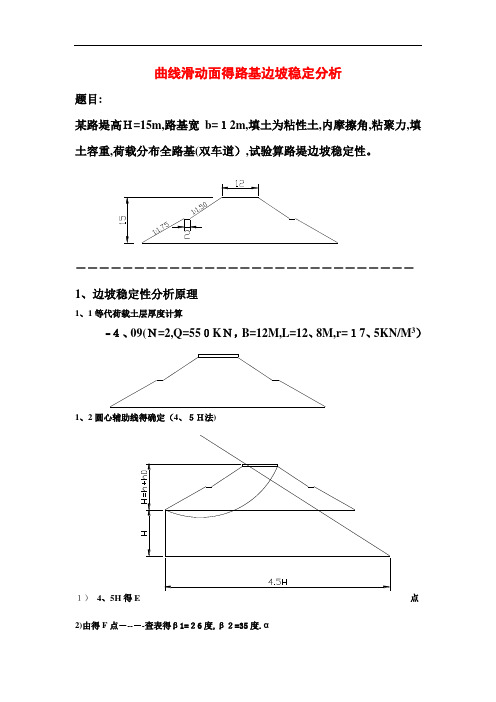
曲线滑动面得路基边坡稳定分析题目:某路堤高H=15m,路基宽b=12m,填土为粘性土,内摩擦角,粘聚力,填土容重,荷载分布全路基(双车道),试验算路堤边坡稳定性。
―――――――――――――――――――――――――――――1、边坡稳定性分析原理1、1等代荷载土层厚度计算=4、09(N=2,Q=550KN,B=12M,L=12、8M,r=17、5KN/M3)1、2圆心辅助线得确定(4、5H法)1)4、5H得E点2)由得F点-----查表得β1=26度,β2=35度.α1、3假设滑动圆弧位置,求圆心位置一般假设圆弧一端经过坡脚点,另一端经过得位置为:路基顶面左边缘、左1/4、中1/2、右1/4、右边缘等处,圆心分别对应O1,O2,O3,O4,O5,分别计算这五种滑动面得稳定安全系数,从中找出最小值。
1、4对滑动土体进行条分------从滑动面顶端(路基上)向左每5m划分一个土条。
1、5在AUTOCAD图中量取各计算数据量取半径各土条得面积各土条横距图--------圆心在O1图-------圆心在O2图-------圆心在O3图------圆心在O4图------圆心在O51、6数据填入EXCEL表格并计算五种滑动面得计算数据汇总3、计算结果分析与结论3、1计算结果分析稳定系数K与滑动面位置变化示意图。
重点说明:稳定系数在滑动面在路基最左端时最大,然后逐渐减小,当滑动面在路基中间时达到最小,为1、51,然后当滑动面在路基上得点继续向右移动时,稳定系数又逐渐增大,到达最右端时为1、64。
3、2结论1)由于Kmin=1、51,大于规范规定得1、20~1、25,故边坡稳定。
2)不满足要求,如何处理:1、减小边坡坡度2、换添路基土,选择粘性系数较大得土3、加固边坡。
