Lingo教程
LINGO应用教程
第十章 LINGOLingo 软件是求解线性规划、非线性规划的数学软件,也可用于一些线性和非线性方程组的求解等。
Lingo 实际上也是最优化问题的一种建模语言,包括许多常用的数学函数供使用者建立优化模型时调用,并可以接受与其他数据文件交换数据。
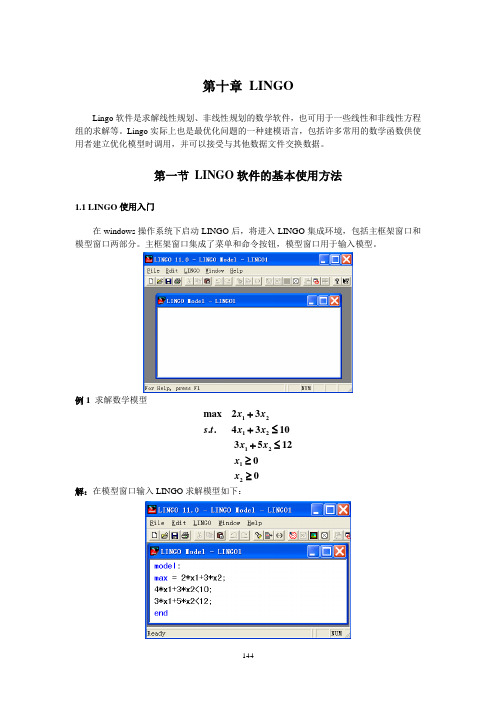
第一节 LINGO 软件的基本使用方法1.1 LINGO 使用入门在windows 操作系统下启动LINGO 后,将进入LINGO 集成环境,包括主框架窗口和模型窗口两部分。
主框架窗口集成了菜单和命令按钮,模型窗口用于输入模型。
例1 求解数学模型12121212max 23..4310351200x x s t x x x x x x ++≤+≤≥≥解:在模型窗口输入LINGO 求解模型如下:输入模型后选择菜单LINGO|Solve 或者按工具栏的,LINGO开始编译模型,如有语法错误将返回一个错误的消息并指明错误出现的位置;如果通过编译,LINGO将激活Solver运算器寻求模型的最优解,首先出现Solver Status状态窗口显示模型求解的运算状态信息:状态窗口显示的信息含义如下:“Global optimal solution found”表示得到全局最优解。
“Objective value: 7.454545”表示最优目标值为7.454545。
“Total solver iterations:2” 表示迭代2次得到结果。
“V alue”给出最优解中各变量的值:x1=1.272727,x2=1.636364。
Reduced Cost 值列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时,目标函数的变化率。
其中基变量的reduced cost值应为0,对于非基变量xj,相应的reduced cost值表示当某个变量xj 增加一个单位时目标函数减少的量( max型问题)。
本例中此值均为0。
SLACK OR SURPLUS值给出约束条件的松驰变量或剩余变量的值。
lingo入门教程(共55张)

3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
第18页,共55页。
分析
(fēnxī)
6 A1 5 6
B1 6 C1
S
3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
假设从S到T的最优行驶路线 P 经过城市C1, 则P中从S到C1的子路也一定 是从S到C1的最优行驶路线; 假设 P 经过城市C2, 则P中从S到C2的子路也一定是从S到C2的最优行驶路线. 因此, 为得到从S到T的最优行驶路线, 只需要先求出从S到Ck(k=1,2)的最 优行驶路线, 就可以方便地得到从S到T的最优行驶路线.
第19页,共55页。
分析
(fēnxī)
6 A1 5 6
B1 6 C1
S
3 3
A2
8 67
A3 4
7
B2
8 9
5 C2 6
T
此例中可把从S到T的行驶过程分成4个阶段,即 S→Ai (i=1,2 或3), Ai → Bj(j=1或2), Bj → Ck(k=1或2), Ck → T. 记d(Y,X)为城 市Y与城市X之间的直接距离(若这两个城市之间没有道路直 接相连,则可以认为直接距离为∞),用L(X)表示城市S到城市
L B2 minL A1 5, L A2 6, L A3 4 7 L A3 4; L C1 minL B1 6, L B2 8 15 L B2 8;
略2去),最小运量136.2275(吨公里)。
1
3
5
0
0
1
2
3
4
5
6
lingo教程_

修改运行时的 内存限制
激活敏感 性分析
LINGO软件菜单——WINDOW
1. 命令行窗口(Open Command Window ) 从窗口菜单中选用“Open Command Window”命令或直接按Ctrl+1可以打开LINGO 的命令行窗口。在命令行窗口中可以获得命 令行界面,在“:”提示符后可以输入LINGO的 命令行命令。 2. 状态窗口(Status Window) 从窗口菜单中选用“Status Window”命 令或直接按Ctrl+2可以打开LINGO的求解状 态窗口。 3. 回到模型窗口(Sent To Back) Ctrl+B 4. 关闭所有窗口(Close All) Ctrl+3 5. 并行放置窗口 (Tile) Ctrl+4 6. 层叠放置窗口(Cascade) Ctrl+5 7. 放置图标(Arrange Icons) Ctrl+6
解的目标函数值
目前为止的 迭代次数
• 运行状态窗口
使用的特殊求解程序 : B-and-B (分枝定界算法) Global (全局最优求解程序) Multistart(用多个初始点求解的程序)
LINGO软件菜单——EIDT
1. 恢复(Undo) 从编辑菜单中选用“恢复”(Undo)命令或按Ctrl+Z组合键,将撤销上 次操作、恢复至其前的状态。 2. 剪切(Cut) 从编辑菜单中选用“剪切”(Cut)命令或按Ctrl+X组合键可以将当前选 中的内容剪切至剪贴板中。 3. 复制(Copy) 从编辑菜单中选用“复制”(Copy)命令、单击“复制”按钮或按Ctrl+C组 合键可以将当前选中的内容复制到剪贴板中。 4. 粘贴(Paste) 从编辑菜单中选用“粘贴”(Paste)命令、单击“粘贴”按钮或按Ctrl+V 组合键可以将粘贴板中的当前内容复制到当前插入点的位置。 5. 粘贴特定..(Paste Special。。) 与上面的命令不同,它可以用于剪贴板中的内容不是文本的情形. 6. 全选(Select All) 从编辑菜单中选用“Select All”命令或按Ctrl+A组合键可选定当前窗口 中的所有内容。 7. 匹配小括号(Match Parenthesis) 从编辑菜单中选用“Match Parenthesis”命令、单击“Match Parenthesis”按钮或按Ctrl+P组合键可以为当前选中的开括号查找匹配的 闭括号。 8. 粘贴函数(Paste Function) 从编辑菜单中选用“Paste Function”命令可以将LINGO的内部函数粘贴 到当前插入点。
LINGO教程(数据输入输出)

14
例:
LLIINNGGOO 教 程
首先,建立相应的EXCEL数据文件 mydata.xls ,并定义相应的数据单元
B4:B7单元 C4:C7单D元4:D7单元E4:E7单元 F4:F7单元 命名为 CITIES 命名为 CO命S名T 为 NEE命D 名为SUPP命LY名为SOLUTION
用于输出结果
已经存在,则覆盖原文件
11
例:
Lingo程序exam0403.LG4(部分) :
输出表头, 并换行
LLIINNGGOO 教 程
@TEXT('exam0403.txt')=@write(4*' ','Value',12*' ','Dual',13*' ', 输出变量Ordered
'Decrease',8*' ','Increase',@newline(2)); @TEXT('exam0403.txt')=@write('Variables:',@newline(2));
• 打开EXCEL文件 • 菜单命令“插入|对象” • 选择“新建|LINDO
Document”,建立一个空的 LINGO文件对象,且在EXCEL 中出现LINGO菜单 • 输入LINGO 程序内容,即可在 EXCEL中运行LINGO程序 •虽然在EXCEL文件中嵌入了LINGO对象,但需要人工干预才能运行这个对象。 •若希望在EXCEL中自动运行一个LINGO程序 ,则需要将LINGO程序用命令脚 本进行描述,并需要用EXCEL的宏命令进行调用。
数据单元定义方法:选择EXCEL的菜单命令“插入|名称|定义” ,才谈出对话框中输入单元名称
LINGO使用教程

§6 LINGO的命令行命令
§7 综合举例
作者 胡志兴
LINGO 教程
LINGO 是用来求解线性和非线性优化问题的简易工具。LINGO 内置了一种建立最优化模 型的语言,可以简便地表达大规模问题,利用 LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门
当你在 windows 下开始运行 LINGO 系统时,会得到类似下面的一个窗口:
·集的名字 ·父集的名字 ·可选,集成员 ·可选,集成员的属性 可用下面的语法定义一个派生集:
setname(parent_set_list)[/member_list/][:attribute_list]; setname 是集的名字。parent_set_list 是已定义的集的列表,多个时必须用逗号隔开。如 果没有指定成员列表,那么 LINGO 会自动创建父集成员的所有组合作为派生集的成员。派 生集的父集既可以是原始集,也可以是其它的派生集。
data: students,sex,age= John 1 16 Jill 0 14 Rose 0 17 Mike 1 13;
《Lingo教程》课件

学习面向对象编程的基本概念和Lingo中的类、对象和继承。
2
继承和多态
掌握继承和多态的概念,以及如何使用它们设计灵活可扩展的程序。
3
使用Lingo进行网络编程
了解如何使用Lingo进行网络通信和数据交换。
4
错误处理
学习如何处理异常和错误,以确保程序的稳定性和利用Lingo开发图形用户界面, 创建直观、互动和易于使用的应 用程序。
游戏制作
使用Lingo创建令人兴奋的游戏, 实现各种令人惊叹的游戏效果。
多媒体应用
探索Lingo在音频、视频和动画 等多媒体应用领域的应用。
Lingo开源社区
Lingo开源社区介绍
了解Lingo开源社区,与其他开发者交流经验和分享资源。
Lingo社区资源分享
探索Lingo社区分享的各种资源,如代码库、教程和文档。
Lingo的应用领域
Lingo常用于游戏开发、动画制作、多媒体交互和图形用户界面设计等领域。
Lingo环境配置
安装Lingo
下载并安装Lingo以开始您的编 程之旅。
Lingo开发环境介绍
了解Lingo的开发环境,掌握各 种工具和功能。
Lingo常用工具
收集有用的Lingo工具,以加快 您的开发效率。
总结
通过本次《Lingo教程》PPT课件,您应该对Lingo的概述、环境配置、基础和高级语法、实例应用、开源社区 以及Lingo的现状和未来有了更深入的了解。希望这些知识能够对您的Lingo开发之旅起到帮助和指导作用。
基础语法
1 变量和常量
2 数据类型
学习如何声明和使用变量和常量以存储数据。
掌握Lingo的不同数据类型,如字符串、数字 和布尔值。
Lingo教程
LINGO教程LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
§1 LINGO快速入门●安装:实验室的所有电脑都已经事先安装好了Lingo 8(或者9, 10, 11)。
如果要在自己的电脑上安装这个软件,建议从网上下载一个破解版的,按照提示一步一步地安装完毕。
●简单例子:当你在windows系统下开始运行LINGO时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都要在该窗口内编码实现。
下面举两个例子。
例 1 某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示。
产品I 产品II设备 1 2 8台时原材料A 4 0 16kg原材料B 0 4 12kg该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应该如何安排生产计划使该厂获利最多?我们用下面的数学模型来描述这个问题。
设x_1、x_2分别表示在计划期内产品I、II的产量。
因为设备的有效台时是8,这是一个限制产量的条件,所以在确定产品I、II的产量时,要考虑不超过设备的有效台时数,即可用不等式表示为x_1 + 2x_2 <=8同理,因原材料A、B的限量,可以得到以下不等式4x_1 <=164x_2 <=12该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x_1、x_2以得到最大的利润。
若用z表示利润,这时z=2x_1+3x_2.综合上述,该计划问题可用数学模型表示为:目标函数 max z=2x_1+3x_2约束条件 x_1 + 2x_2 <=84x_1 <=164x_2 <=12x_1、x_2 >=0一个优化模型一般有三部分组成:1.目标函数(Objective Function):要达到的目标。
LINGO教程(PDF)
例 2.3
sets: product/A B/; machine/M N/; week/1..2/; allowed(product,machine,week):x; endsets
LINGO 生成了三个父集的所有组合共八组作为 allowed 集的成员。列表如下: 编号 成员 1 (A,M,1)
共 53 页 4
注意:用“[]”表示该部分内容可选。下同,不再赘述。
Setname 是你选择的来标记集的名字,最好具有较强的可读性。集名字必须严格符合标 准命名规则:以拉丁字母或下划线(_)为首字符,其后由拉丁字母(A—Z) 、下划线、阿拉 伯数字(0,1,…,9)组成的总长度不超过 32 个字符的字符串,且不区分大小写。
LINGO 教程
LINGO 是用来求解线性和非线性优化问题的简易工具。LINGO 内置了一种建立最优化模型 的语言,可以简便地表达大规模问题,利用 LINGO 高效的求解器可快速求解并分析结果。
§1 LINGO 快速入门
当你在 windows 下开始运行 LINGO 系统时,会得到类似下面的一个窗口:
共 53 页 3
LINGO 教程
MonthM..MonthN MonthYearM..MonthYearN
Oct..Jan Oct2001..Jan2002
Oct,Nov,Dec,Jan Oct2001,Nov2001,Dec2001,Jan2002
③ 集成员不放在集定义中,而在随后的数据部分 数据部分来定义。 数据部分 例 2.2
共 53 页 1
LINGO 教程
A3 A4 A5 A6 销量
5 7 2 5 35
2 6 3 5 37
1 7 9 2 22
9 3 5 2 32
2024年度LINGO基本教程完整版PPT大纲
2024/2/2
1
目录
2024/2/2
• 引言 • LINGO编程基础 • 线性规划问题求解 • 整数规划与非线性规划问题求解 • 约束条件处理技巧 • 优化算法介绍与应用 • 实际问题建模与求解案例分析 • 课程总结与展望
2
01
引言
Chapter
2024/2/2
拉格朗日乘子法
引入拉格朗日乘子,构造拉格朗 日函数,将等式约束问题转化为 无约束优化问题。
罚函数法
将等式约束条件转化为某种形式 的罚函数,加入到目标函数中, 通过求解无约束优化问题得到近 似解。
2024/2/2
22
不等式约束条件处理方法
积极约束法
将不等式约束条件转化为等式约束条件,引 入松弛变量,构造新的目标函数进行求解。
24
06
优化算法介绍与应用
Chapter
2024/2/2
25
梯度下降法原理及在LINGO中实现
01
梯度下降法基本原理
通过迭代求解目标函数的最小值,每次迭代沿着当前位置的负梯度方向
前进一段距离,直到达到最小值或满足停止条件。
2024/2/2
02 03
LINGO中实现梯度下降法
在LINGO中,可以使用内置函数或自定义程序来实现梯度下降法。需要 定义目标函数、梯度函数和迭代步长等参数,并通过循环迭代来逼近最 小值。
在LINGO中,可以使用内置函数或自定义程序来实现牛顿 法。需要定义目标函数、一阶导数和二阶导数等参数,并 通过循环迭代来逼近根。
牛顿法的优缺点
牛顿法具有收敛速度快、精度高等优点,但需要计算二阶 导数矩阵,计算量较大,且对初始值有一定要求。
LINGO教程
INV (0) 10
MIN
I 1, 2, 3, 4
{400 RP(I ) 450OP(I ) 20 INV (I )}
加上变量的非负约束
26
LINGO 教 程
用DEM,RP,OP,INV分别表示需求量、正常生产的产量、 加班生产的产量、库存量,则DEM,RP,OP,INV对每个 季度都应该有一个对应的值,也就说他们都应该是一 个由4个元素组成的数组,其中DEM是已知的,而 25RP,OP,INV是未知数。
LINGO 教 程
问题的模型(可以看出是LP模型 ) 目标函数是所有费用的和 约束条件主要有两个: 1)能力限制: RP ( I ) 40, I 1,2,3,4 2)产品数量的平衡方程:
23
LINGO 教 程
1. LINGO入门 2.在LINGO中使用集合
3. 运算符和函数
2.在LINGO中使用集合 4. LINGO的主要菜单命令 5. LINGO命令窗口 6.习题
24
LINGO 教 程
集合的基本用法和LINGO模型的基本要素
例 SAILCO公司需要决定下四个季度的帆船生产量。下 理解LINGO建模语言最重要的是理解集合(Set)及其 四个季度的帆船需求量分别是40条,60条,75条,25条, 属性(Attribute)的概念。 这些需求必须按时满足。每个季度正常的生产能力是40 条帆船,每条船的生产费用为400美元。如果加班生产, 每条船的生产费用为450美元。每个季度末,每条船的 库存费用为20美元。假定生产提前期为0,初始库存为 10条船。如何安排生产可使总费用最小?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LINGO教程LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
§1 LINGO快速入门●安装:实验室的所有电脑都已经事先安装好了Lingo 8(或者9, 10, 11)。
如果要在自己的电脑上安装这个软件,建议从网上下载一个破解版的,按照提示一步一步地安装完毕。
●简单例子:当你在windows系统下开始运行LINGO时,会得到类似于下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model –LINGO1的窗口是LINGO的默认模型窗口,建立的模型都要在该窗口内编码实现。
下面举两个例子。
例 1某工厂在计划期内要安排生产I、II两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表所示。
产品I 产品II设备 1 2 8台时原材料A 4 0 16kg原材料B 0 4 12kg该工厂每生产一件产品I可获利2元,每生产一件产品II可获利3元,问应该如何安排生产计划使该厂获利最多?我们用下面的数学模型来描述这个问题。
设x_1、x_2分别表示在计划期内产品I、II的产量。
因为设备的有效台时是8,这是一个限制产量的条件,所以在确定产品I、II的产量时,要考虑不超过设备的有效台时数,即可用不等式表示为x_1 + 2x_2 <=8同理,因原材料A、B的限量,可以得到以下不等式4x_1 <=164x_2 <=12该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x_1、x_2以得到最大的利润。
若用z表示利润,这时z=2x_1+3x_2.综合上述,该计划问题可用数学模型表示为:目标函数 max z=2x_1+3x_2约束条件 x_1 + 2x_2 <=84x_1 <=164x_2 <=12x_1、x_2 >=0一般来说,一个优化模型将由以下三部分组成:1.目标函数(Objective Function):要达到的目标。
2.决策变量(Decision variables):每组决策变量的值代表一种方案。
在优化模型中需要确定决策变量的最优值,优化的目标就是找到决策变量的最优值使得目标函数取得最优。
3.约束条件(Constraints):对于决策变量的一些约束,它限定决策变量可以取的值。
在写数学模型时,一般第一行是目标函数,接下来是约束条件,再接着是一些非负限制等。
在模型窗口输入如下代码:Max = 2*x1+3*x2;!This is a linear program.X1+2*x2<=8;4*x1<16;4*x2<12;注意:1.每一个lingo表达式最后要跟一个分号;2.多数电脑中没有 符号,lingo中<=代替;为了方便可以用<代替小于等于,用>代替大于等于。
3.我们可以添加一些注释,增加程序的可读性。
注释以一个!(叹号必须在英文状态下输入,它会自动变为绿色)开始,以;(分号)结束。
4.Lingo中不区分变量名的大小写。
变量名必须以字母(A-Z)开头,后面的字符可以是字母、数字、下划线。
变量名不能超过32个字符。
点击工具栏上的按钮或者用Lingo菜单下的solve求解这个模型,如果模型没有语法错误,即可得到如下结果。
Global optimal solution found. 已经找到全局最优解Objective value: 14.00000 目标函数值Infeasibilities: 0.000000 不可行的约束数Total solver iterations: 1 迭代次数Variable Value Reduced CostX1 4.0000000.000000X2 2.0000000.000000Row Slack or Surplus Dual Price1 14.000001.0000002 0.0000001.5000003 0.0000000.12500004 4.0000000.000000Reduced Cost()非基变量变为基变量时目标函数的系数必须的增加值。
Dual Price(对偶价格或者影子价格)在编译阶段没有语法错误,lingo会调用内部的求解器开始为你的模型搜索最优解,还最后会显示一个求解状态窗口:求解状态窗口内各项:Variables Box(变量框)●Total: 模型中的变量总个数(total number of variables in the model)●Nonlinear: 模型中非线形变量的个数(the number of the total variablesthat are nonlinear)注: X * X + Y = 100; 中X是非线性变量,Y是线性变量。
●Integer: 模型中整数变量的个数(total number of integer variablesin the model)注意:计算各种变量个数时,不计算可以确定变量值的变量。
如:如果约束条件中x=10,那么这个变量不被看做是一个变量Constraints Box●Total:所有的约束条件个数(total constraints in the expanded model)●Nonlinear:所有的非线性约束的个数(the number of these constraintsthat are nonlinear)Nonzeroes Box(约束框)Total:模型中非零系数的个数。
Nonlinear:非线性变量个数。
如果一个约束条件里中的所有变量都是确定的,则约束条件不进行计数。
The Nonzeros box shows the total nonzero coefficients in the model and the number of these that appear on nonlinear variablesNonzeroes Box(非零框)显示该模型的总非零系数和非线性的这些变量出现的数目。
Generator Memory Used Box求解时使用的内存量Elapsed Runtime Box求解模型时用的时间,这个会受电脑运行的其他程序的影响。
Solver Status BoxExtended Solver Status BoxLingo程序的一些规则:1.在Lingo中最开始都是“MAX=”或者“MIN=”开始表示求目标函数的最大或者最小值。
2.变量和它前面的系数之间要用“*”连接,中间可以有空格。
3.变量名不区分大小写,但必须以字母开始,不超过32个字符。
4.数学表达式结束时要用分号“;”表示结束。
表达式可以写在多行上,但是表达式中间不能用分号。
5.在电脑系统中一般没有“小于等于”符号,在Lingo采用“<=”来表示“小于等于”,用“>=”表示“大于等于”。
小于等于也可以用更简单的“<”表示,大于等于用“>”表示。
Lingo模型语言:例1.2运输问题使用LINGO软件计算6个仓库8个销售地的最小费用运输问题。
产销单位运设VOLUME_i_j为从仓库i运送到销售地j那里的货物量,那么我们的目标函数可以表示为:MIN = 6 * VOLUME_1_1 + 2 * VOLUME_1_2 +6 * VOLUME_1_3 +7 * VOLUME_1_4 +4 * VOLUME_1_5 +...8 * VOLUME_6_5 + VOLUME_6_6 + 4 * VOLUME_6_7+3 * VOLUME_6_8;这里我们只列出了48个项中的9项,输入这么多的数据非常麻烦,而且容易出错。
而运用Lingo提供的模型语言则可以很容易的来描述这个目标函数,而且很容易扩充模型。
在数学上可以用数学符号表示目标函数为:Minimize Σij COST ij • VOLUME ij运用Lingo模型语言来描述上面的目标函数,这样的描述简短,容易输入,容易读,更容易理解。
MIN = @SUM( LINKS(I,J): COST(I,J) * VOLUME(I,J));也就是说,在仓库和销售地之间的所有可能运送调价下求运送总运费最小。
接下来看约束条件:在模型里有两类约束,第一类是销售地要得到需要的货物量,我们称这类约束为需求约束。
第二类称为容量限制,每个仓库运出的货物量不能大于它的库存量。
先考虑第一个销售地的约束,VOLUME_1_1 + VOLUME_2_1 + VOLUME_3_1 +VOLUME_4_1 + VOLUME_5_1 +VOLUME_6_1 = 35;剩下还要输入7个类似的约束。
用运用数学符号表述这个约束:Σi VOLUMEij = DEMANDj, 对每个销售地j成立。
对应的Lingo模型语言描述是:@FOR( VENDORS( J):@SUM( WAREHOUSES( I): VOLUME( I, J)) =DEMAND( J));类似的仓库的容量限制用Lingo语言描述为:@FOR( WAREHOUSES( I):@SUM( VENDORS( J): VOLUME( I, J))<=CAPACITY( I));目前我们得到下面的Lingo模型:MODEL:MIN = @SUM( LINKS( I, J):COST( I, J) * VOLUME( I, J));@FOR( VENDORS( J):@SUM( WAREHOUSES( I): VOLUME( I, J)) =DEMAND( J));@FOR( WAREHOUSES( I):@SUM( VENDORS( J): VOLUME( I, J)) <=CAPACITY( I));End但是我们还要定义一些变量。
集合段:在我们已经得到的程序里有一些量没有定义,如WAREHOUSES( I),DEMAND( J), LINKS( I, J)。
这些量将在Lingo中的集合段定义。
集合段以SETS:表示开始,以ENDSETS表示结束。
如果一个集合的元素都已经定义过,就可以用一些循环函数(如@for).上面的三个集合在Lingo的集合段定义为:SETS:WAREHOUSES: CAPACITY;VENDORS: DEMAND;LINKS(WAREHOUSES, VENDORS): COST, VOLUME;ENDSETSWAREHOUSES: CAPACITY;这一句表示在集合WAREHOUSES上有一个属性CAPACITY,即每个仓库都有一个容量属性。
