高中数学优等生辅导题目
专题09圆锥曲线-2021年新高考数学尖子生培优题

2021年高考数学尖子生培优题典(新高考专版)专题09 圆锥曲线姓名:__________________ 班级:______________ 得分:_________________一、单选题1.椭圆22154x y +=的长轴长是( )A .2B .4C .D .10【答案】C【解析】因为椭圆的方程是22154x y +=, 所以25a =,解得a =,所以长轴长是2a =2.双曲线22221124x y m m−=+−的焦距是( )A .4B .C .8D .【答案】C【解析】由题意可得,c 2�a 2+b 2�m 2+12+4�m 2�16 �c =4 焦距2c �8 3.抛物线214y x =的焦点坐标是( )A .1,016B .()1,0C .1-,016D .()0,1【答案】D 【解析】214y x =即24x y =,所以其焦点在y 轴正半轴,坐标为()0,1 4.抛物线212x y =的准线方程为( ) A .18y =− B .18y =C .12x =−D .12x =【答案】A【解析】解:由于抛物线22x py =的准线方程为2p y =−, 则有抛物线212x y =的准线方程是18y =−. 5.已知12F F 、是双曲线2222:1x y E a b−=的左、右焦点,过点1F 且与x 轴垂直的直线与双曲线左支交于点,M N ,已知2MF N ∆是等腰直角三角形,则双曲线的离心率是( ).A B .2C .1+D .2+【答案】C【解析】由题意得222222210,11b c c a ac e e e e a=⇒−=⇒−−=>⇒=6.焦点在x 轴上的椭圆222125x y a +=焦距为8,两个焦点为12,F F ,弦AB 过点1F ,则2ABF 的周长为( )A .20B .28C .D .【答案】D【解析】解:因为焦点在x 轴上的椭圆222125x y a += 焦距为8,所以22254a −=,解得a =如图,根据椭圆的定义可得122AF AF a +=,122BF BF a +=,所以22211224ABF C AB AF BF AF BF AF BF a =++=+++== 故选:D7.抛物线24y x =的焦点到双曲线221x y −=的渐近线的距离为( )A .12BCD .2【答案】B【解析】因为抛物线的焦点为(1,0),双曲线的渐近线为0x y ±=,所以抛物线的焦点到双曲线的渐近线的距离为d8.已知抛物线2:2C y px =的焦点为F ,过F 的直线l 与C 交于,A B 两点(设点A 在第一象限),分别过,A B 作准线的垂线,垂足分别为11,A B ,若1AFA 为等边三角形,1BFB 的面积为1S ,四边形11A B BF 的面积为2S ,则12S S =( )A .13B .14C .16D .17【答案】D【解析】由条件可得1160AFx AFA A FO °∠=∠=∠=,1130BFB OFB °∠=∠=,直线AB的方程为2p yx − ,与22y px =联立,消去y ,整理得2233504p x px −+=,解得6p x =或32p x =,故3,,26p pA B ,则1|2|||623p p p BF BB ==+=,则1BFB的面积为11262p p S =×+ 11A B BF的面积为2S p p=+−⋅=,故1217S S =.二、多选题9.已知抛物线()220y px p =>上一点M 到其准线及对称轴的距离分别为3和p 的值可以是( ) A .2 B .6C .4D .8【答案】AC【解析】设M 的横坐标为x ,由题意,32px +=,28px =,解得2p =或4p =. 10.在平面直角坐标系xOy 中,已知双曲线221412x y −=,则( )A .实轴长为2 B.渐近线方程为y =C .离心率为2D .一条渐近线与准线的交点到另一条渐近线的距离为3【答案】BC【解析】由双曲线方程221412x y −=,得2a =,b =4c ==,所以实轴长24a =,故选项A 错误;渐近线方程为b y x a=±,故选项B 正确; 离心率2cea==,故选项C 正确; 准线方程21a x c=±=±,取其中一条准线1x =,y =与1x =的交点(A ,点A到直线y =的距离dD 错误.11.已知F 是抛物线2:16C y x =的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则( )A .C 的准线方程为4x =−B .F 点的坐标为()0,4C .12FN = D.三角形ONF 的面积为(O 为坐标原点)【答案】ACD【解析】如图,不妨设点M 位于第一象限,设抛物线的准线l 与x 轴交于点F ′,作MB l ⊥于点B ,NA l ⊥于点A . 由抛物线的解析式可得准线方程为4x =−,F 点的坐标为()4,0,则4AN =,8FF ′=,在直角梯形ANFF ′中,中位线62AN FF BM′+==,由抛物线的定义有6MF MB ==,结合题意,有6MN MF ==,故6612FN FM NM =+=+=,ON =,142QNF S =×=△.12.已知曲线22:1C mx ny +=.( ) A .若m >n >0,则C 是椭圆,其焦点在y 轴上 B .若m =n >0,则CC .若mn <0,则C是双曲线,其渐近线方程为y = D .若m =0,n >0,则C 是两条直线 【答案】ACD【解析】对于A ,若0m n >>,则221mx ny +=可化为22111x y m n+=, 因为0m n >>,所以11m n<, 即曲线C 表示焦点在y 轴上的椭圆,故A 正确;对于B ,若0m n =>,则221mx ny +=可化为221x y n+=, 此时曲线C的圆,故B 不正确; 对于C ,若0mn <,则221mx ny +=可化为22111x y m n+=, 此时曲线C 表示双曲线,由220mx ny +=可得y =,故C 正确; 对于D ,若0,0m n =>,则221mx ny +=可化为21y n=,y =,此时曲线C 表示平行于x 轴的两条直线,故D 正确;三、填空题13.双曲线2213x y −=的焦距长为_______.【答案】4【解析】1,a b==,222c a b =+ ,2c ∴=,焦距长24c=.14.以双曲线22145x y −=的焦点为顶点,顶点为焦点的椭圆方程为_____.【答案】22195x y +=【解析】由双曲线的相关性质可知,双曲线22:145x y C -=的焦点为(3,0)±,顶点为(20)±,,所以椭圆的顶点为(3,0)±,焦点为(20)±,,因为2225b a c =-=,所以椭圆的方程为22195x y +=15.已知抛物线()220y px p =>的焦点为F ,准线为l ,C :()(2216x a y −+−=过点F 且与l相切,则p =______. 【答案】2或6【解析】解:02p F,在()(2216x a y −+−=上所以(220162p a −+−=,即22pa −=(1), ()(2216x a y −+−=和与l 相切,42pa +=(2), 由(1)(2)得,所以2p =或6p =16.如图,椭圆E 的左右焦点为1F ,2F ,以2F 为圆心的圆过原点,且与椭圆E 在第一象限交于点P ,若过P 、1F 的直线l 与圆2F 相切,则直线l 的斜率k =______;椭圆E 的离心率e =______.1 【解析】连接2PF ,由于l 是圆2F 的切线,所以12PF PF ⊥.在12Rt PF F 中,212PF OF OF c ===, 所以21212PF F F =,所以126PF F π∠=,所以直线l的斜率6tan πk ==. 1PF =,根据椭圆的定义可知1212212F F c cea aPF PF ====−+.四、解答题17.求适合下列条件的椭圆标准方程:(1)与椭圆2212x y +=有相同的焦点,且经过点3(1,)2(2)经过(2,(A B 两点 【解析】(1)椭圆2212x y +=的焦点坐标为(1,0)±,∵椭圆过点3(1,)2,∴24a ==,∴2,a b ==,∴椭圆的标准方程为22143x y +=.(2)设所求的椭圆方程为221(0,0,)x y m n m n m n+=>>≠.把(2,(A B 两点代入, 得:14213241mnm n+=+= ,解得81m n ==,, ∴椭圆方程为2218x y +=.18.已知双曲线22221(0,0)y x a b a b−=>>的一个焦点在直线:3120l y ++=上,且其一条渐近线与直线l 平行,求该双曲线的方程.【解析】依题意得,双曲线的焦点在y 轴上,又直线l 与y 轴的交点为(0,4)−,所以双曲线的一个焦点坐标为(0,4)−,即4c ==.又因为直线l的斜率为a b =224,12a b ==, 故双曲线的方程为221412y x −=.19.已知抛物线22(0)y px p =>的准线方程为1x =−. (Ⅰ)求p 的值;(Ⅱ)直线:1l y x =−交抛物线于A 、B 两点,求弦长AB .【解析】(Ⅰ)依已知得12p =,所以2p =; (Ⅱ)设()11,A x y ,()22,B x y ,由214y x y x =− =消去y ,得2610x x −+=, 则126x x +=,121x x =,所以AB =8=. 20.已知双曲线()2222:10,0x y C a b a b −=>>的一个焦点与抛物线28y x =的焦点相同,且经过点(2,3). (Ⅰ)求双曲线C 的标准方程和其渐近线方程; (Ⅱ)设直线l 经过点(0,1)−,且斜率为k .求直线l 与双曲线C 有两个公共点时k 的取值范围.【解析】(Ⅰ)由已知,双曲线的焦点为(2,0)−和(2,0)根据定义有:221a a −⇒= 故21a =,24c =,23b =,从而所求双曲线C 的方程为2213y x −=其渐近线方程为:y =.(Ⅱ)由22133y kx x y =− −= 得:()223240k x kx −+−=当230k −≠,即k ≠时,若>0∆,即()()22244(4)31240k k k ∆=−−−=−>24022k k ⇒−>⇒−<<时, 直线与双曲线相交,有两个公共点;所以,当22k −<<,且k ≠时,直线与双曲线有两个公共点.21.已知椭圆M :22219x y b+=(0b >)的一个焦点为()2,0,设椭圆N 的焦点恰为椭圆M 短轴上的顶点,且椭圆N 过点. (1)求N 的方程;(2)若直线2y x =−与椭圆N 交于A ,B 两点,求AB .【解析】(1)由椭圆M :22219x y b+=(0b >)的一个焦点为()2,0,得2c =,且222945b a c =−=−=,∴椭圆N 的焦点为(0,,(.又椭圆N 过点,∴椭圆N∴椭圆N 1.∴N 的方程为2216y x +=;(2)设()11,A x y ,()22,B x y , 联立22216y x y x =− +=消去y ,整理得27420x x −−=, 则1247x x +=,1227x x =−, ∴127AB =. 22.已知动圆Q 经过定点()0,F a ,且与定直线:l y a =−相切(其中a 为常数,且0a >).记动圆圆心Q 的轨迹为曲线C .(1)求C 的方程,并说明C 是什么曲线? (2)设点P 的坐标为()0,a −,过点P 作曲线C 的切线,切点为A ,若过点P 的直线m 与曲线C 交于M ,N 两点,证明:AFM AFN ∠=∠.【解析】(1)设(),Q x y,由题意得y a =+,化简得24x ay =, 所以动圆圆心Q 的轨迹方程为24x ay =, 它是以F 为焦点,以直线l 为准线的抛物线.(2)不妨设()2,04t A t t a >. 因为24x y a=,所以2x y a ′=, 从而直线PA 的斜率为2402t a t a t a+=−,解得2t a =,即()2,A a a , 又()0,F a ,所以//AF x 轴.要使AFM AFN ∠=∠,只需0FM FN k k +=. 设直线m 的方程为y kx a =−,代入24x ay =并整理, 得22440x akx a −+=.所以()221610a k ∆=−>,解得1k <−或1k >. 设()11,M x y ,()22,N x y ,则124x x ak +=,2124x x a =. ()()2112121212FM FN x y a x y a y a y a k k x x x x −+−−−+=+= ()()()21121212122222x kx a x kx a a x x k x x x x −+−+==− 224204a ak k a ⋅=−=. 故存在直线m ,使得AFM AFN ∠=∠, 此时直线m 的斜率的取值范围为()(),11,−∞−∪+∞.。
专题06不等式-2021年新高考数学尖子生培优题

2021年高考数学尖子生培优题典(新高考专版)专题06 不等式姓名:__________________ 班级:______________ 得分:_________________一、 选择题1.不等式112x <的解集为( ) A .(,2)−∞ B .(2,)+∞C .(0,2)D .(,0)(2,)−∞+∞【答案】D【解析】112x <等价于202x x−<即()20x x −>, 故不等式的解为0x <或2x >,故解集为()(),02,−∞+∞ ,选D.2.设,a b ∈R ,若0a b −>,则下列不等式中正确的是( ) A .0b a −> B .330a b +<C .220a b −<D .0b a +>【答案】D【解析】利用赋值法:令1,0a b ==排除A,B,C,选D. 3.若正实数,a b ,满足1a b +=,则33b a b+的最小值为( )A .2B .C .5D .【答案】C【解析】根据题意,若正实数,a b ,满足1a b +=,则33333235333b b a b b a a b a b a b ++=+=+++= ,当且仅当334b a ==时等号成立, 即33b a b+的最小值为5; 4.已知0,0,22x y x y >>+=,则xy 的最大值为( )A .12B .1CD .14【答案】A【解析】解:∵x >0,y >0,且2x +y =2,∴xy =12(2x •y )≤12(22x y +)2=12,当且仅当x =12,y =1时取等号, 故则xy 的最大值为12,故选A 5.若点P (x , y )在以A (-3,1),B (-1,0),C (-2,0)为顶点的△ABC 的内部运动(不包含边界),则21y x −−的取值范围是 A .1[,1]2B .1(,1)2C .1[,1]4D .(1,14)【答案】D【解析】根据已知的条件可知,点A,B ,C 围成的三角形ABC ,其内动点P (x,y ),那么所求的为动点P 与定点M (1,2)两点的斜率的取值范围,则根据已知中的三点A ,B,C 的坐标,分别求解12,1,43AMBM CM k k k ===,则利用倾斜角与斜率的关系,结合正切函数图象可得,21y x −−的取值范围是(1,14),选D. 6.已知不等式ax 2+bx +2>0的解集为{x |-1<x <2},则不等式2x 2+bx +a <0的解集为( )A .1|12x x −<<B .{1x <−或12x >C .{x |-2<x <1}D .{x |x <-2或x >1}【答案】A【解析】由题意知x =-1,x =2是方程ax 2+bx +2=0的根,则-1+2=-b a ,-1×2=2a, 解得a =-1,b =1.所以2x 2+bx +a =2x 2+x -1<0,解得-1<x <12. 7.已知a b >,则下列各式一定正确的是( ) A .lg lg a x b x > B .22ax bx > C .22a b > D .22x x a b ⋅>⋅【答案】D【解析】因为2x 恒为正数,故选D .8.若直线ax +2by -2=0(a >0,b >0)始终平分圆x 2+y 2-4x -2y -8=0的周长,则1a+2b 的最小值为( ) A .1 B .5C .D .3+【答案】D【解析】由题意知圆心C (2,1)在直线ax +2by -2=0上, ∴2a +2b -2=0,整理得a +b =1,∴1a +2b =12ab + ⋅(a +b )=3+b a +2a b ≥3+3+当且仅当b a =2a b,即b =2,a -1时,等号成立.∴1a +2b的最小值为3+.9.若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是( )A .(,8][0,)−∞−+∞B .(),4−∞−C .[8,4)−−D .(,8]−∞−【答案】D【解析】由9(4)340x x a ++⋅+=,得443(4)0,(4)3433xxx x a a +++=∴−+=+≥(当且仅当32x =时等号成立),解得8a ≤−10.函数()21f x nx x =+− (0,)bx a b a R +>∈的图像在点()(),b f b 处的切线斜率的最小值是( )A .BC .1D .2【答案】D【解析】11()2()2f x x b k f b b x b ′′=+−∴==+≥= ,当且仅当1b =时取等号,因此切线斜率的最小值是2,选D.11.已知a ,b ∈R 且ab ≠0,对于任意x ≥0 均有(x –a )(x–b )(x–2a–b )≥0,则( ) A .a <0 B .a >0C .b <0D .b >0【答案】C【解析】因为0ab ≠,所以0a ≠且0b ≠,设()()()(2)f x x a x b x a b =−−−−,则()f x 的零点为123,,2x a x b x a b ===+ 当0a >时,则23x x <,1>0x ,要使()0f x ≥,必有2a b a +=,且0b <, 即=−b a ,且0b <,所以0b <;当0a <时,则23x x >,10x <,要使()0f x ≥,必有0b <. 综上一定有0b <.12.设,,a b c 为实数,且0a b <<,则下列不等式正确的是( ) A .11a b< B .22ac bc <C .b a a b> D .22a ab b >>【答案】D【解析】对于A ,令1112,1,,12a b a b=−=−=−=−,故A 错误; 对于B ,当0c 时,则220ac bc ==,故B 错误;对于C ,则11a b>,1,2b a =−=−,则b aa b <,故C 错误; 对于D ,20,a b aab <∴ 且2ab b >,故D 正确,故选D.13.在关于x 的不等式2(1)0x a x a −++<的解集中至多包含2个整数,则a 的取值范围是 ( )A .(3,5)−B .(2,4)−C .[3,5]−D .[2,4]−【答案】D【解析】 因为关于x 的不等式2(1)0x a x a −++<可化为(1)()0x x a −−<, 当1a >时,不等式的解集为1x a <<, 当1a <时,不等式的解集为1<<a x ,要使得解集中至多包含2个整数,则4a ≤且2a ≥−, 所以实数a 的取值范围是[2,4]a ∈−,故选D.14.已知0x >,0y >,23x y +=,则23x y xy+的最小值为( )A .3−B .1+C 1D 1+【答案】B【解析】已知0x >,0y >,23x y +=,则22223(2)22111x y x x y y x xy y x yxy xy xy y x +++++===+++= ,当且仅当222x y = 时,即当3x =−,且y =故23x y xy+的最小值为1+15.已知函数()212x x f x e e mx +−=−−在R 上为增函数,则m 的取值范围为( )A .(,−∞B .)+∞C .(,−∞D .)+∞【答案】C【解析】因为函数()212x x f x ee mx +−=−−在R 上为增函数,所以()212220x x f x e e m +−+′=−≥在R 上恒成立, 即21222x x e e m +−≥+在R 上恒成立,因为21222x x e e +−≥+14x =−时取“=”号,所以m 的取值范围为(,−∞,16.函数()f x 、()g x 分别是定义在R 上的偶函数、奇函数,且()()2xf xg x e +=,若存在2(]0,x ∈,使不等式()()20f x mg x −≤成立,则实数m 的最小值为( )A .4B .C .8D .【答案】B【解析】∵()()2xf xg x e +=,①∴()()2xf xg x e −−+−=,又函数()f x 、()g x 分别是定义在R 上的偶函数、奇函数, ∴()2()x f x g x e −−=,②由①②得1()()2x x f x e e −=+,1()()4x x g x e e −=−, 不等式()()20f x mg x −≤为2211()()024x x x x e e m e e −−+−−≤,(*), 设x x t e e −=−,这是一个增函数,当02]x ∈(,时,221(0,]t e e∈−, (*)变为21202t mt +−≤,22(2)22()t m t t t+≥=+,若存在2(]0,x ∈,使不等式()()20f x mg x −≤成立,则为:存在221(0,]t e e∈−,使22()m t t ≥+成立,由于22()2t t+≥×,当且仅当2t t =,即t =时等号成立,∴22()2t +的最小值是.∴m ≥. 故选:B.17.(多选题)下列命题为真命题的是() A .若0a b >>,则22ac bc >B .若0a b <<,则22a ab b >>C .若00a b c >><且,则22c ca b> D .若a b >且11a b>,则0ab < 【答案】BCD【解析】选项A :当0c 时,不等式不成立,故本命题是假命题;选项B: 2222,00a b a ba ab ab b a ab b a b << ⇒>⇒>∴>><< ,所以本命题是真命题;选项C: 22222211000,0c c a b a b c a b a b >>⇒>>⇒<<<∴> ,所以本命题是真命题; 选项D: 2111100,00b aa b b a ab a b a b ab−>⇒−>⇒>>∴−<∴< ,所以本命题是真命题,所以本题选BCD.18.(多选题)设1,1a b >>,且()1ab a b −+=,那么( )A .+a b 有最小值)21B .+a b 有最大值)21+C .ab 有最大值3+D .ab 有最小值3+【答案】AD【解析】解:①由题已知得:22a b ab + ≤,故有2()4()40a b a b +−+−≥,解得2a b +≥+或2a b +≤−+(舍),即2a b +≥(当且仅当1a b ==+时取等号),A 正确;②因为a b +≥,所以()a b −+≤−,()ab a b ab −+≤−又因为()1ab a b −+=1ab ≤−21ab ⇒≤−+,)221≤1⇒−≥1≥3ab ⇒≥+ab有最小值3+,D 正确.故选AD19.(多选题)已知函数2()(0)f x x ax b a =++>有且只有一个零点,则( ) A .224a b −≤ B .214a b+≥ C .若不等式20x ax b +−<的解集为()12,x x ,则120x x >D .若不等式2x ax b c ++<的解集为()12,x x ,且124x x −=,则4c = 【答案】ABD【解析】因为2()(0)f x x ax b a =++>有且只有一个零点,故可得240a b =−= ,即可240a b =>.对A :224a b −≤等价于2440b b −+≥,显然()220b −≥,故A 正确;对B :21144a b b b +=+≥=,故B 正确; 对C :因为不等式20x ax b +−<的解集为()12,x x ,故可得120x x b =−<,故C 错误; 对D :因为不等式2x ax b c ++<的解集为()12,x x ,且124x x −=,则方程2 0x ax b c ++−=的两根为12,x x ,4,故可得4c =,故D 正确.20.(多选题)设,x y R +∈,S x y =+,P xy =,以下四个命题中正确的是( ).A .若P 为定值m ,则S 有最大值B .若S P ,则P 有最大值4C .若S P ,则S 有最小值4D .若2S kP ≥总成立,则k 的取值范围为4k ≤ 【答案】CD【解析】P 为定值m 时,S 应有最小值A 不正确;当S P 时,x y xy xy +=⇒≥min 244xy P ⇒≥⇒≥⇒=,∴B 不正确;2min ()444x y S P x y xy x y S +=⇒+=≤⇒+≥⇒=,当且仅当2xy ==,等号成立,∴C 正确; 由22S S kP k P⇒≤≥,又2222224S x y xy xy xy P xy xy +++=≥=, ∴2min 4S P= ,∴4k ≤,∴D 正确. 二、 解答题21.已知正数a ,b ,c 满足1abc =,求证:(2)(2)(2)27a b c +++≥.【解析】证明:由正数a ,b ,c 满足1abc =, 则(2)(2)(2)a b c +++(11)(11)(11)a b c ++++++333≥27=27=(当且仅当1a b c ===时等号成立),22.已知不等式(1)若对于所有的实数不等式恒成立,求的取值范围;(2)设不等式对于满足的一切的值都成立,求的取值范围. 【解析】(1)不存在这样的使得不等式恒成立(2){xx |−1+√72<xx <1+√32} (1)当mm =0时,1−2xx <0,即当xx >12时不等式不恒成立,不满足条件当mm ≠0时,设ff (xx )=mmxx 2−2xx −mm +1,由于ff (xx )<0恒成立,则有�mm <04−4mm (1−mm )<0 解得mm ∈φφ综上所述,不存在这样的使得不等式恒成立.(2)由题意−2≤mm ≤2,设gg (xx )=(xx 2−1)mm +(1−2xx ),则有�gg (−2)<0gg (2)<0 即�−2xx 2−2xx +3<02xx 2−2xx −1<0,解得−1+√72<xx <1+√32 所以的取值范围为{xx |−1+√72<xx <1+√32}23.已知函数()21f x x x =−−+.(1)解不等式()2f x <;(2)若正实数m ,n 满足3m n +=,试比较122m n +与()32f x −的大小,并说明理由. 【解析】(1)①当1x ≤−时,()()212x x −−++<,无解; ②当12x −<<时,()()212x x −−−+<,122x −<<; ③当2x ≥时,()()212x x −−+<,恒成立,2x ≥, 所以该不等式的解集为12x x>−. (2)因为|()21213x x x x −−+≤−−+≤, 当有仅当()()210x x −⋅+≥,即1x ≤−或2x ≥时取“=”, 所以()33f x −≤≤,即()933222f x −≤−≤. 又1212112322233222m n n m m n m n m n + ++⋅+++≥ , 当且仅当22n m m n =,即1m =,2n =时取等号, 所以()12322f x m n +≥−. 24.已知函数()211f x x x =−++. (1)求不等式()2f x x ≤+的解集;(2)若函数()y f x =的最小值记为m ,设0a >,0b >,且有a b m +=.求1212a b +++的最小值.【解析】解(1)因为()3,1,12112,1,213,.2x x f x x x x x x x −<− =−++=−+−≤≤ >从图可知满足不等式()2f x x ≤+的解集为[]0,1.(2)由图可知函数()y f x =的最小值为32,即32m =. 所以32a b +=,从而9122a b +++=, 从而()()112121212912a b a b a b +=++++ ++++ ()21222339129a b a b + +=++≥+= ++ 当且仅当()21212a b a b ++=++,即a b ∴1212a b +++25.某工厂生产某种商品的年固定成本为250万元,每生产()x x N ∗∈千件需另投入成本为()C x (万元).当年产量不足80千件时,21()103C xx x =+(万元);当年产量不小于80千件时,10000()511450C x x x=+−(万元).通过市场分析,每件售价为500元最为合适. (1)写出年利润L (万元)关于年产量x (千件)的函数解析式; (2)该产品年产量为多少千件时,该厂所获利润最大?【解析】(1)依题意2**110080,3()1000051145080,x x x x N C x x x x N x +<<∈ = +−≥∈, 2**140250080,350()25010000120080,x x x x N L x C x x x x N x −+−<<∈ =−−= −−+≥∈, (2)由(1)得当*080,x x N <<∈时,221140250(60)95033L x x x =−+−=−−+, 当60x =时,max 950L =万元, 当*80,x x N ≥∈时,10000()120012001000L x x=−++≤−+=, 当且仅当10000100x x=时,等号成立,即max 1000L =万元 所以利润的最大值为1000万元.答:该产品年产量为100千件时,该厂所获利润最大.。
21-22学年上学期高一数学尖子生培优题典(人教B版2019)(能力篇含答案解析)01 函数的单调性

专题01 函数的单调性题组一 函数的单调性例题1-1 已知函数()122xxf x ⎛⎫=- ⎪⎝⎭,则()f x ( )A .是偶函数,且在R 上是增函数B .是奇函数,且在R 上是增函数C .是偶函数,且在R 上是减函数D .是奇函数,且在R 上是减函数解题思路:______________________________________________________________________________________________________________________________________________________跟踪训练1-1 函数()()22log 32f x x x =-+的单调递增区间是( )A .3,2⎛⎫-∞ ⎪⎝⎭B .3,2⎛⎫+∞ ⎪⎝⎭C .()2,+∞D .(),1-∞解题思路:______________________________________________________________________________________________________________________________________________________例题1-2 已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数,那么a 的取值范围是( ) A .(0,1) B .11,73⎡⎫⎪⎢⎣⎭C .10,3⎛⎫ ⎪⎝⎭D .1,17⎡⎫⎪⎢⎣⎭解题思路:______________________________________________________________________________________________________________________________________________________跟踪训练1-2 若函数,1()(34)1,1x a x f x a x x ⎧>=⎨-+≤⎩是R 上的减函数,则实数a 的取值范围是( )A .30,4⎛⎫ ⎪⎝⎭B .3,14⎛⎫ ⎪⎝⎭C .34,45⎛⎤ ⎥⎝⎦D .4,15⎡⎫⎪⎢⎣⎭解题思路:______________________________________________________________________________________________________________________________________________________题组二 函数的单调性综合运用1、已知函数()2f x x ax =-(1)若在区间[)1,+∞上是增函数,求实数a 的取值范围; (2)求函数()f x 在区间[]1,2上的最小值.2、已知函数()224lg 43y x x x =--+-的定义域为M . (Ⅰ)求M ;(Ⅱ)当x M ∈时,求函数1()4328x x f x +=-⋅+的最小值及此时x 的值.3、已知函数1()log [(1)2]af x a x =--(0a >且1a ≠).(1)求()f x 的定义域;(2)若()0f x >在51,4⎡⎤⎢⎥⎣⎦上恒成立,求实数a 的取值范围.专题01 函数的单调性题组一 函数的单调性例题1-1 已知函数()122xxf x ⎛⎫=- ⎪⎝⎭,则()f x ( )A .是偶函数,且在R 上是增函数B .是奇函数,且在R 上是增函数C .是偶函数,且在R 上是减函数D .是奇函数,且在R 上是减函数【详解】因为()22xxf x -=-的定义域是R ,()()22xx f x f x --=-=-f x 为奇函数,又()f x 是R 上的增函数, 故选:B.跟踪训练1-1 函数()()22log 32f x x x =-+的单调递增区间是( )A .3,2⎛⎫-∞ ⎪⎝⎭B .3,2⎛⎫+∞ ⎪⎝⎭C .()2,+∞D .(),1-∞【详解】函数()()22log 32f x x x =-+,所以2320x x -+>,解得1x <或2x >, 所以()f x 定义域为()(),12,-∞⋃+∞又因函数()()22log 32f x x x =-+是复合函数,其外层函数2log y t =为增函数,所以要使()f x 为增函数,则内层232t x x =-+是增函数, 则32x >所以可得()f x 单调增区间为()2,+∞ 故选:C .例题1-2 已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩是(,)-∞+∞上的减函数,那么a 的取值范围是( ) A .(0,1)B .11,73⎡⎫⎪⎢⎣⎭C .10,3⎛⎫ ⎪⎝⎭D .1,17⎡⎫⎪⎢⎣⎭【详解】由题意可知31001(31)14log 1a a a a a -<⎧⎪<<⎨⎪-⨯+≥⎩,即130117a a a ⎧<⎪⎪<<⎨⎪⎪≥⎩,则11,73a ⎡⎫∈⎪⎢⎣⎭故选:B跟踪训练1-2 若函数,1()(34)1,1x a x f x a x x ⎧>=⎨-+≤⎩是R 上的减函数,则实数a 的取值范围是( )A .30,4⎛⎫⎪⎝⎭B .3,14⎛⎫ ⎪⎝⎭C .34,45⎛⎤ ⎥⎝⎦D .4,15⎡⎫⎪⎢⎣⎭【详解】因为函数,1()(34)1,1x a x f x a x x ⎧>=⎨-+≤⎩是R 上的减函数,所以01340341a a a a<<⎧⎪-<⎨⎪-+≥⎩,解得3445a <≤,所以实数a 的取值范围是34,45⎛⎤ ⎥⎝⎦. 故选:C.题组二 函数的单调性综合运用1、已知函数()2f x x ax =-(1)若在区间[)1,+∞上是增函数,求实数a 的取值范围; (2)求函数()f x 在区间[]1,2上的最小值.【详解】解:(1)函数()2f x x ax =-的对称轴方程为2a x =,因为函数()f x 区间[)1,+∞上是增函数,所以12a≤ 所以2a ≤; (2)①当12a≤即2a ≤时,函数()f x 区间[]1,2上是增函数, 所以()()min 11f x f a ==-; ②当22a≥即4a ≥时,函数()f x 区间[]1,2上是减函数, 所以()()min 242f x f a ==-; ③当122a<<即24a <<时, 函数()f x 区间1,2a ⎛⎫ ⎪⎝⎭上是减函数,在,22a ⎛⎫⎪⎝⎭上时增函数 所以()2min24a a f x f ⎛⎫==- ⎪⎝⎭,综上所述:当2a ≤时,()()min 11f x f a ==-, 当4a ≥时,()()min 242f x f a ==-; 当24a <<时,()2min24a a f x f ⎛⎫==- ⎪⎝⎭;2、已知函数()224lg 43y x x x =--+-的定义域为M . (Ⅰ)求M ;(Ⅱ)当x M ∈时,求函数1()4328x x f x +=-⋅+的最小值及此时x 的值.【详解】 (Ⅰ)要使()224lg 43y x x x =--+-有意义,则2240430x x x ⎧-≥⎨-+->⎩,解得12x <≤, 所以(1,2]=M ;(Ⅱ)由题意,函数()21()43282(1,628,2]x x xx x f x +=-⋅+=-⋅+∈,令(,224]xt =∈,则()()22831,6(2,4]t h t t t t +=--∈=-, 所以当3t =即2log 3x =时,函数()h t 取最小值1-, 所以函数()f x 的最小值为1-,此时2log 3x =.3、已知函数1()log [(1)2]af x a x =--(0a >且1a ≠).(1)求()f x 的定义域;(2)若()0f x >在51,4⎡⎤⎢⎥⎣⎦上恒成立,求实数a 的取值范围.【详解】 (1)因为1()log [(1)2]af x a x =--,所以(1)20a x -->,因为0a >且1a ≠,当01a <<时,10a -<,解不等式(1)20a x -->可得21x a <-; 当1a >时,10a ->,解不等式(1)20a x -->可得21x a >-; 综上,当01a <<时,函数的定义域为2,1a ⎛⎫-∞ ⎪-⎝⎭;当1a >时,函数的定义域为2,1a ⎛⎫+∞⎪-⎝⎭; (2)当01a <<时,10a -<,11a>,所以函数1()log [(1)2]a f x a x =--在定义域内单调递减;又且()0f x >在514⎡⎤⎢⎥⎣⎦,上恒成立,所以只需152415log (1)204a a a ⎧<⎪-⎪⎨⎡⎤⎪-->⎢⎥⎪⎣⎦⎩,无解;当1a >时,10a ->,101a<<,所以函数1()log [(1)2]a f x a x =--在定义域内单调递减;又()0f x >在51,4⎡⎤⎢⎥⎣⎦上恒成立,所以只需12115log (1)204a a a ⎧>⎪-⎪⎨⎡⎤⎪-->⎢⎥⎪⎣⎦⎩,即35(1)214a a >⎧⎪⎨--<⎪⎩,解得1735a <<,综上所述实数a 的取值范围为173,5⎛⎫⎪⎝⎭.。
上海市2021届高三上学期高考数学专题复习优等生练习卷2份(12月) 含答案

值范围是
9.
已知双曲线 x2 a2
y2 b2
1( a 0 ,b 0 )的左、右焦点分别为 F1 、F2 ,直线 l 过点 F2 且
与双曲线有且仅有一个交点,直线 l 与一条渐近线交于点 P ,且 PF2F1 2PF1F2 ,则双 曲线的渐近线方程为
10.
243 不等式
(x 2)5
9 x5 3x (x 2)
x
y60
,则 2x ( 1)y 的取值范围为
y 1
2
6.
若 (1 2x2 )(1
1)n 的展开式中所有项的系数和为 96,则展开式中含 x
1 x2
项的系数是
7. 函数 f (x) 2sin x 与函数 g(x) 3 x 1 的图像所有交点的横坐标之和为
8. 已知平面向量 a 、 b 、 c 满足 | a || b | 2 , a b , (a c) (b c) ,则 (a b) c 的取
5. 记 (2 x)7 a0 a1(1 x) a2(1 x)2 a7(1 x)7 ,则 a1 a2 a7 6. 从 6 男 2 女共 8 名学生中选出队长 1 人,副队长 1 人,普通队员 2 人组成 4 人服务队,
要求服务队中至少有 1 名女生,共有
种不同的选法
7.
设各项均为正数的数列
3.
已知 tan
2 ,则 sin2
sin 2 sin cos
cos 2
1
的值为
4. 将一个质地均匀的正四面玩具(四个面上依次标有 1,2,3,4,)先后抛掷两次,得到
的点数依次记为 a 、 b ,则事件“ 2a b 0 ”发生的概率为
x 3y 6 0
5.
若实数 x 、
高中数学培优训练一(含详细解析及答案)

高中数学培优训练一高等数学一直以来被莘莘学子认为是不可逾越的大山,其实不然,只要掌握适当的方法与技巧,多进行一些培优训练,多对思维做一些培优性的练习,就一定能克服困难,成为“学霸”,轻松解决试卷中的培优题!!!1.已知椭圆C,12,F F 是椭圆的两个焦点,P 是椭圆上任意一点,且21F PF ∆(1)求椭圆C 的方程;(2)设圆TT 的两条切线交椭圆于F E ,两点,当圆心在x 轴上移动且()1,3t ∈时,求EF 的斜率的取值范围.2.若函数()f x 是定义域D 内的某个区间I 上的增函数,且在I 上是减函数,则称()y f x =是I 上的“单反减函数”(1)判断()f x 在(]0,1上是否是“单反减函数”;(2)若()g x 是[)1,+∞上的“单反减函数”,求实数a 的取值范围.3.如图,在四棱锥ABCD P -中,⊥PA 底面ABCD ,底面ABCD 是梯形,其中 BC AD //,AD BA ⊥,AC 与BD 交于点O ,M 是AB 边上的点,且BM AM 2=,已知4==AD PA ,3=AB ,2=BC .(1)求平面PMC 与平面PAD 所成锐二面角的正切;(2)已知N 是PM 上一点,且//ON 平面PCD ,求 4.已知等差数列{}n a 满足121, a a =、73a -、8a 成等比数列,数列{}n b 的前n 项和1n n T a =-(其中a 为正常数)(1)求{}n a 的前项和n S ;(2)已知*2a N ∈,1122n n n I a b a b a b =++⋅⋅⋅+,求n IA PB C OMN5.设(),R f x a b λ∈=⋅,其中()cos ,sin ,sin cos ax x b x λ⎛==- ,已知()f x 满足(1)求函数()f x 的单调递增区间;(26.(本题满分14分)各项为正的数列{}n a 满足 (1)取1n a λ+=,求证:数列(2)取2λ=时令,记数列{}n b 的前n 项和为n S ,数列{}n b 的前n 项之积为n T ,求证:对任意正整数n ,12n n n T S ++为定值7.(本题满分15分)函数2()22(,,0)f x ax bx a b a b a =--+∈>R ,()22g x ax b =-(1时,求(sin )f θ的最大值; (2)设0a >时,若对任意θ∈R ,都有|(sin )|1f θ≤恒成立,且(sin )g θ的最大值为2,求()f x 的表达式.8.(本题满分15(1)求椭圆方程;(2)Rt ABC ∆以(0,)A b 为直角顶点,边,AB BC 与椭圆交于,B C 两点,求ABC ∆ 面积的最大值.9.(本题满分14分)已知函数R a x a x a x x f ∈++-=,ln )12()(2(1)当,1=a 求)(x f 的单调区间; (2)a >1时,求)(x f 在区间[]e ,1上的最小值; (3),)1()(x a x g -=若使得))(00x g x f (≥成立,求a 的范围. 10.(本小题满分13分)已知抛物线21:2(0)C y px p =>的焦点F 以及椭圆焦点及左、右顶点均在圆22:1O x y +=上.(1)求抛物线1C 和椭圆2C 的标准方程;(2)过点F 的直线交抛物线1C 于A 、B 两不同点,交y 轴于点N ,已知1212,,:NA AF NB BF λλλλ==+求证为定值.11.(本小题满分12分)已知数列{}n a 的前项n 和为n S ,点))(,(*∈N n S n n 均在函数x x x f 23)(2-=的图象上。
高中数学培优试题及答案

高中数学培优试题及答案一、选择题(每题5分,共20分)1. 若函数f(x)=2x^2-4x+3,求f(2)的值为:A. 1B. 3C. 5D. 7答案:B2. 已知等差数列{an}的首项a1=3,公差d=2,求第10项a10的值:A. 23B. 27C. 29D. 31答案:A3. 计算下列定积分的值:∫(0,2) (x^2 - 3x + 2) dx:A. 0B. 4C. 6D. 8答案:C4. 若复数z满足|z-1|=2,则z的模长|z|的最小值为:A. 1B. √3C. 2D. √5答案:B二、填空题(每题5分,共20分)5. 函数y=x^3-3x^2+4x-5的极值点个数为_______。
答案:26. 一个圆的半径为5,圆心在原点,求该圆的面积为_______。
答案:25π7. 已知函数f(x)=x^2-2x+1,求f(x)的对称轴方程为_______。
答案:x=18. 若直线y=3x+2与抛物线y^2=4x相交于点A和B,求线段AB的中点坐标为_______。
答案:(1, 5/3)三、解答题(每题15分,共30分)9. 已知等比数列{bn}的前三项依次为b1=2,b2=4,b3=8,求该数列的通项公式。
答案:bn=2^n10. 已知函数f(x)=x^3-3x^2+2x+1,求函数f(x)的单调递增区间。
答案:(-∞, 1)和(2, +∞)四、证明题(每题15分,共15分)11. 证明:若a, b, c为实数,且满足a^2+b^2+c^2=1,则(a+b+c)^2≤3。
答案:证明如下:由柯西-施瓦茨不等式可知,对于任意实数a, b, c有(a^2+b^2+c^2)(1^2+1^2+1^2)≥(a+b+c)^2,即(a^2+b^2+c^2)(3)≥(a+b+c)^2。
又因为a^2+b^2+c^2=1,所以(a+b+c)^2≤3。
五、应用题(每题15分,共15分)12. 某商场进行促销活动,规定顾客每消费满100元即可获得一张优惠券,每张优惠券可以抵用10元。
专题04 平面向量-2021年高考数学尖子生培优题典(新高考专版)(解析版)

高考数学尖子生培优题典(新高考专版)专题04 平面向量姓名:__________________ 班级:______________ 得分:_________________一、 选择题A .2B .2-C .1D .1-【答案】A【解析】解:∵a b ⊥;∴20a b x ⋅=-+=; ∴x=2.A .()2,1-B .()2,1-C .()2,0D .()4,3【答案】B【解析】由题意得()()()3,11,22,1b a -=-=-,故选B.A B C D .【答案】A【解析】解:由a b a b -=+,得0a b ⋅=,所以10-+=,则m =.∴()21a =-= A .1 B .3C .1或3D .4【答案】C【解析】根据题意,得()24,3a b m -=-,由()2b a b ⊥-,得()430m m --=.解得1m =或 3.m =故选C.A .14B .12C .1D .2【答案】A【解析】因为()1,a m =,()2,1b =, 所以()31,31a b m -=-,因为()//3c a b -,所以()3141m -⨯=-,解得14m =,A .6π B .4π C .3π D .2π 【答案】A【解析】由已知可得:22a b a -= ,得3a b = ,设向量a 与b 的夹角为θ ,则3cos .2a b a bθ==⨯ 所以向量a 与b 的夹角为6π A .1 B .1- C .6- D .6【答案】D【解析】因为()()2112a b =-=-,,, 所以()()23,0(2,1)3206a b a +⋅=⋅-=⨯+=A .13AB AC +B .13AB AC -C .2133AB AC + D .1233AB AC + 【答案】C【解析】因为D 是BC 上一点,且13BD BC =,则()11213333AD AB BD AB BC AB BA AC AB AC =+=+=++=+.A .12-B .12C .4-D .4【答案】D所以20,12cos40,4a b b πλλλ⋅-=∴⨯⨯-=∴=A .3144AB AD + B .1142AB AD -+ C .12AB AD + D .3144AB AD -+ 【答案】B【解析】()111111222224BF BC CF BC CE BC BE BC BC BE BC BA =+=+=+-=+=+1124AD AB =-A .23BG BE =B .3AB AC AG +=C .12DG AG =D .0GA GB GC ++=【答案】C【解析】因为AD ,BE ,CF 分别是边BC ,CA ,AB 上的中线,它们交于点G , 所以点G 是ABC 的重心.选项A :因为点G 是ABC 的重心,所以23BG BE =,因此23BG BE =,所以本选项正确; 选项B :因为AD 是边BC 上的中线,所以2AB AC AD +=,又因为点G 是ABC 的重心,所以有2332AG AD AD AG =⇒=,因此3AB AC AG +=,所以本选项正确; 选项C :因为点G 是ABC 的重心,所以2AG DG =,因此1122DG GA AG ==-,所以本选项不正确; 选项D :因为AD 是边BC 上的中线,点G 是ABC 的重心,所以有20GA GB GF CG GA GB GC +==⇒++=,因此本选项正确.AB C D 【答案】D【解析】由题可知2sin sin cos cos A B A C C A =,2sin sin A B B =,则sin A =,3A π=或23π.又AG =,延长AG 交BC 于点D ,所以AD =因为()12AD AB AC =+,所以()2214AD AB AC =+,即()2221||2cos 4AD b c bc A =++,当3A π=时,3c =,所以ABC ∆的面积为1sin 2bc A =23A π=时,4c =,所以ABC ∆的面积为1sin 2bc A =.A .911B .511C .311D .211【答案】C 【解析】由13AN NC =,可得4AC AN =, 所以281111AP mAB AC mAB AN =+=+, 又,,B P N 三点共线,由三点共线定理,可得:8111m +=, 311m ∴=,A .(3,6)-B .(3,6)-C .(6,3)-D .(6,3)-【答案】A【解析】设(,)b x y =,则cos1802,a b x y =-(1)2x y -=- (1)=(2), 由(1)(2)可解得x=-3,y=6故选A ; A .30 B .60︒ C .120︒D .150︒【答案】A【解析】设a 与b 夹角为θ,[]0,θπ∈()()3a b a b -⊥-∴()()30a b a b -⋅-=整理可得:()()22403aa b b-⋅+=,即22403a a b b -⋅+=1a =,代入22403a a b b -⋅+=可得2340a b b -⋅+=可得:24cos 30a b b θ-+=,即24cos 03b b θ-+=整理可得:3cos 2444343b b bbθ=+≥⨯=当且仅当344b b=,即3b =取等号故cos θ≥,结合[]0,θπ∈, 根据余弦函数图象可知θ最大值:6πA B C .5D .13【答案】B【解析】由已知326//0,,4p q x x ∴--⨯=∴=-,(2,3),||13p q p q +=-+=.故选:B .A .两个有共同始点且相等的向量,其终点可能不同B .若非零向量AB 与CD 共线,则A 、B 、C 、D四点共线C .若非零向量a 与b 共线,则a b =D .四边形ABCD 是平行四边形,则必有AB CD = 【答案】ABC【解析】A 中,相等向量的始点相同,则终点一定也相同,所以A 中命题不正确;B 中,向量AB 与CD 共线,只能说明AB 、CD 所在直线平行或在同一条直线上,所以B 中命题不正确;C 中,向量a 与b 共线,说明a 与b 方向相同或相反,a 与b 不一定相等,所以C 中命题不正确;D 中,因为四边形ABCD 是平行四边形,所以AB 与CD 是相反向量,所以||||AB CD =,所以D 中命题正确.A .AB AC ⊥;B .四边形ABCD 为平行四边形;C .AC 与BD 夹角的余弦值为; D .85AB AC +=【答案】BD【解析】由(2,4),(4,1),(9,5),(7,8)A B C D ,所以()2,3AB =-,()7,1AC =,()2,3DC =-, ()3,7BD =,对于A ,143110AB AC ⋅=-=≠,故A 错误;对于B ,由()2,3AB =-,()2,3DC =-,则AB DC =, 即AB 与DC 平行且相等,故B 正确;对于C ,cos ,50AC BD AC BD AC BD⋅===C 错误;对于D ,()||9,2AB AC +=-=,故D 正确;A .若a →与b →垂直,则1m =-B .若//a b →→,则a b →→⋅的值为5-C .若1m =,则a b →→-=D .若2m =-,则a →与b →的夹角为60︒【答案】BC【解析】对于选项A :由a b ⊥,可得()()1120m ⨯-+-⋅=,解得12m =-,故A 错误, 对于选项B :由//a b →→,可得()()1210m ⨯--⨯-=,解得2m =,∴()1,2b =-,∴()()11225a b ⋅=⨯-+-⨯=-,故B 正确;对于选项C :若1m =,则()2,3a b -=-,则a b →→-=,故C 正确:若2m =-,对于选项D :()1,2b =--:设a 与b 的夹角为θ,则3cos 55a b a bθ⋅===⨯,故D 错误.A .0AB AC AD +-=B .0DA EB FC ++=C .若3||||||AB AC ADAB AC AD +=,则BD 是BA 在BC 的投影向量 D .若点P 是线段AD 上的动点,且满足BP BA BC λμ=+,则λμ的最大值为18【答案】BCD 【解析】如图所示:对选项A ,20AB AC AD AD AD AD +-=-=≠,故A 错误.对选项B ,111()()()222DA EB FC AB AC BA BC CA CB ++=-+-+-+ 111111222222AB AC BA BC CA CB =------1111110222222AB AC AB BC AC BC =--+-++=,故B 正确.对选项C ,||AB AB ,||AC AC ,||ADAD 分别表示平行于AB ,AC ,AD 的单位向量, 由平面向量加法可知:||||AB ACAB AC +为BAC ∠的平分线表示的向量.因为3||||||ABACADAB AC AD +=,所以AD 为BAC ∠的平分线, 又因为AD 为BC 的中线,所以AD BC ⊥,如图所示:BA 在BC 的投影为cos BD BA B BA BD BA ,所以BD 是BA 在BC 的投影向量,故选项C 正确.对选项D ,如图所示: 因为P 在AD 上,即,,A P D 三点共线,设(1)BP tBA t BD ,01t ≤≤. 又因为12BD BC =,所以(1)2t BP tBA BC .因为BP BA BC λμ=+,则12tt λμ=⎧⎪⎨-=⎪⎩,01t≤≤.令21111()2228t y t t ,当12t =时,λμ取得最大值为18.故选项D 正确.二、 解答题(1)用a ,b 表示OC ,DC ;(2)若OE OA λ=,求λ.【解析】解:(1)∵2OC OB OA +=,∴22OC OA OB a b =-=-, 252233DC OC OD a b b a b =-=--=-.(2)∵(2)(2)CE OE OC a a b a b λλ=-=--=-+,又由E 在CD 上,CE 与DC 共线,∴存在实数μ,使CE DC μ=.即5(2)23a b a b λμ⎛⎫-+=- ⎪⎝⎭,则22513λμμ-=⎧⎪⎨=-⎪⎩.解方程组,得45λ=.(1)若m n ,求k 的值;(2)当=2k 时,求m 与n 夹角的余弦值.【解析】解 (1)由题意,得12(),)2,1(m k k n ==,---+.因为m n ,所以()12)12(k k ⨯⨯+=---,解得3k =-.(2)当2k =时,,)3(4n -=.设m 与n 的夹角为θ,则||||m ncos m n θ⋅=5==.所以m 与n . (1)若,a b 为锐角,求x 的范围;(2)当(2)(2)a b a b +⊥-时,求x 的值. 【解析】(1)若,a b 为锐角,则0a b ⋅>且,a b 不同向20,2a b x x ⋅=+>∴>- 当12x =时,,a b 同向122x x ∴>-≠且(2)2(12,4),(2)(2,3)a b x a b x +=+-=-∴21)(2)340x x +-+⨯=(,223140x x -++=即,722x x ==-解得:或 已知ABC ∆的角A 、B 、C 所对的边分别是a 、b 、c ,设向量(,)m a b =,(sin ,n B = sin )A ,(2,2)p b a =--.(1)若//m n ,求证:ABC ∆为等腰三角形;(2)若m p ⊥,边长2c =,角π3C =,求ABC ∆的面积. 【解析】⑴因为,所以sin sin a A b B =,即··22a b a b R R =,其中R 是ABC ∆的外接圆半径, 所以a b =,所以ABC ∆为等腰三角形.⑵因为m p ⊥,所以()()220a b b a -+-=.由余弦定理可知,()22243a b ab a b ab =+-=+-,即()2340ab ab --=解方程得:4ab =(1ab =-舍去)所以11sin 4sin 223S ab C π==⨯⨯=(1)求向量n ;(2)若向量n 与向量()1,0q =的夹角为2π,向量2cos ,2cos 2C p A ⎛⎫= ⎪⎝⎭,其中,,A B C 为ABC 的内角,且2B A C =+.求n p +的取值范围. 【解析】(1)设(),n x y =,由1m n ⋅=-,可得1x y +=-,①n 与向量m 夹角为34π,有3cos 4m m n n π⋅=⋅⋅,1n ∴=,则221x y +=,② 由①②解得10x y =-⎧⎨=⎩或01x y =⎧⎨=-⎩,即()1,0n =-或()0,1n =-; (2)由n 与q 垂直知,()0,1n =-,由2B A C =+ , 知22,,0333B A C A πππ=+=<<,若()0,1n =-,则 2cos ,2cos 1(cos ,cos )2Cn p A A C ⎛⎫+=-= ⎪⎝⎭ 则22221cos 21cos 2()cos cos 22n ACn p A C p ++=+=+=++1411cos 2cos 21cos 22323A A A ππ⎡⎤⎛⎫⎛⎫=++-=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦由203A π<<,则52333A πππ<+<,则11cos 232A ⎛⎫-≤+< ⎪⎝⎭π,则1151cos 22234A ⎛⎫≤++< ⎪⎝⎭π,故215,24n p ⎡⎫∈+⎪⎢⎣⎭,得222n p ⎡⎫∈⎪⎢⎪⎣⎭+.。
高中数学培优班专题资料(包含答案)
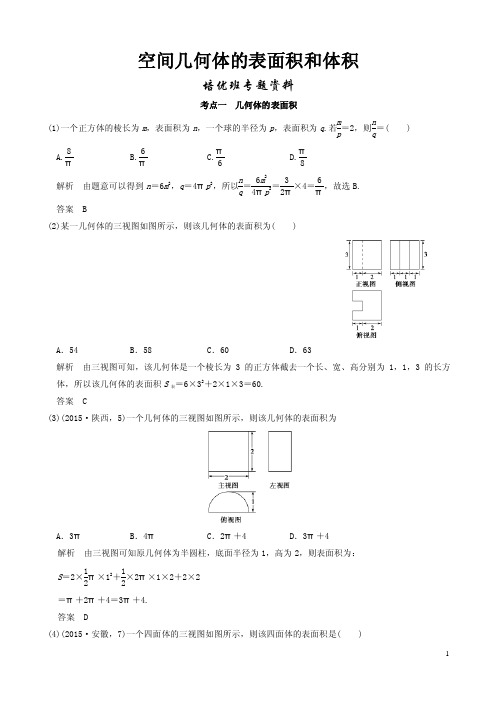
空间几何体的表面积和体积培优班专题资料考点一 几何体的表面积(1)一个正方体的棱长为m ,表面积为n ,一个球的半径为p ,表面积为q .若m p =2,则n q=( ) A.8πB.6πC.π6D.π8解析 由题意可以得到n =6m 2,q =4πp 2,所以n q =6m 24πp 2=32π×4=6πB. 答案 B(2)某一几何体的三视图如图所示,则该几何体的表面积为( )A .54B .58C .60D .63解析 由三视图可知,该几何体是一个棱长为3的正方体截去一个长、宽、高分别为1,1,3的长方体,所以该几何体的表面积S 表=6×32+2×1×3=60. 答案 C(3)(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为A .3πB .4πC .2π+4D .3π+4解析 由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:S =2×12π×12+12×2π×1×2+2×2=π+2π+4=3π+4. 答案 D(4)(2015·安徽,7)一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2解析 由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 答案 B(5)(2015·新课标全国Ⅱ,9)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36πB .64πC .144πD .256π解析 如图,要使三棱锥O -ABC 即C -OAB 的体积最大,当且仅当点C 到平面OAB 的距离,即三棱锥C -OAB 底面OAB 上的高最大,其最大值为球O 的半径R ,则V O -ABC 最大=V C -OAB 最大=13×12S △OAB ×R =13×12×R 2×R =16R 3=36,所以R =6,得S 球O =4πR 2=4π×62=144π,选C. 答案 C(6)(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为( )A .54B .60C .66D .72解析 该几何体的直观图如图所示,易知该几何体的表面是由两个直角三角形,两个直角梯形和一个矩形组成的,则其表面积S =12×3×4+12×3×5+2+52×5+2+52×4+3×5=60.选B.答案 B(7)(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 2解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为S =3×5+2×12×4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm 2).答案 D(8)(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B .16πC .9πD.27π4解析 设球的半径为R ,由题意可得(4-R )2+(2)2=R 2,解得R =94,所以该球的表面积为4πR 2=81π4.故选A.(9)(2014·安徽,7)一个多面体的三视图如图所示,则该多面体的表面积为( )A .21+ 3B .18+3C .21D .18解析 根据题意作出直观图如图,该多面体是由正方体切去两个角而得到的,根据三视图可知其表面积为6(22-12×1×1)+2×34×(2)2=6×72+3=21+ 3.故选A.答案 A(10)(2012·安徽,12)某几何体的三视图如图所示,该几何体的表面积是________.解析 由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,故该几何体的表面积为S=2×12×(2+5)×4+[2+5+4+42+(5-2)2]×4=92.答案 92考点二 几何体的体积(1)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .2 B.92 C.32D .3解析 根据三视图判断几何体为四棱锥,其直观图是:V =13×1+22×2x =3⇒x =3. 故选D. 答案 D(2)(2015·山东,7)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3B.4π3C.5π3D .2π解析 如图,由题意,得BC =2,AD =AB =1.绕AD 所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体.所求体积V =π×12×2-13π×12×1=53π.答案 C(3)(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B.23+π C.13+2π D.23+2π解析 这是一个三棱锥与半个圆柱的组合体,V =12π×12×2+13⎝⎛⎭⎫12×1×2×1=π+13,选A.答案 A (4)(2015·新课标全国Ⅱ,6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.15解析 如图,由题意知,该几何体是正方体ABCD -A 1B 1C 1D 1被过三点A 、B 1、D 1的平面所截剩余部分,截去的部分为三棱锥A -A 1B 1D 1,设正方体的棱长为1,则截去部分体积与剩余部分体积的比值为111111A A B D B C D ABCDV V --=1111111111A AB D A BCD ABCD A A B D V V V ----=13×12×12×113-13×12×12×1=15,选D.答案 D(5)某几何体的三视图如图所示,它的体积为()A .72πB .48πC .30πD .24π解析 由三视图可知,该几何体是半个球体和一个倒立圆锥体的组合体,球的半径为3,圆锥的底面半径为3,高为4,则根据体积公式可得几何体的体积为30π,故选C.答案 C(6)(2014·陕西,5)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B .4πC .2πD.4π3解析 如图为正四棱柱AC 1.根据题意得AC =2,∴对角面ACC 1A 1为正方形,∴外接球直径2R =A 1C =2,∴R =1,∴V 球=4π3,故选D.答案 D(7)(2014·湖北,8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( ) A.227B.258C.15750D.355113解析 圆锥的体积V =13πr 2h =13π⎝⎛⎭⎫L 2π2h =L 2h 12π,由题意得12π≈752,π近似取为258,故选B.答案 B(8)(2014·新课标全国Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析 由三视图知该零件是两个圆柱的组合体.一个圆柱的底面半径为2 cm ,高为4 cm ;另一个圆柱的底面半径为3 cm ,高为2 cm.则零件的体积V 1=π×22×4+π×32×2=34π(cm 3).而毛坯的体积V =π×32×6=54π(cm 3),因此切削掉部分的体积V 2=V -V 1=54π-34π=20π(cm 3),所以V 2V =20π54π=1027.故选C.答案 C (9)(2012·新课标全国,11)已知三棱锥S ABC 的所有顶点都在球O 的球面上, △ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26B.36C.23D.22解析 如图,H 为△ABC 的外接圆圆心,则∠BHC =120°,设△ABC 的外接圆半径为r ,则1=BC 2=HC 2+HB 2-2HC ·HB ·cos 120°=3r 2, ∴r =33. 连接OH ,根据球的截面性质知,OH ⊥平面ABC ,∴OH =OC 2-CH 2=1-13=63∵O 为SC 的中点,∴S 到平面ABC 的距离为2OH =263,∴V S ABC =13S △ABC ×263=13×34×263=26.答案 A(10)(2015·江苏,9)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为________.解析 设新的底面半径为r ,由题意得13πr 2·4+πr 2·8=13π×52×4+π×22×8,解得r =7.答案7(11)(2014·江苏,8)设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________.解析 设圆柱甲的底面半径为r 1,高为h 1,圆柱乙的底面半径为r 2,高为h 2.由题意得S 1S 2=πr 21πr 22=94,∴r 1r 2=32. 又∵S 甲侧=S 乙侧,即2πr 1h 1=2πr 2h 2,∴h 1h 2=r 2r 1=23, 故V 1V 2=S 1h 1S 2h 2=S 1S 2·h 1h 2=94×23=32答案 32(12)(2013·江苏,8)如图,在三棱柱A 1B 1C 1ABC 中,D ,E ,F 分别是AB ,AC ,AA 1的中点,设三棱锥F ADE 的体积为V 1,三棱柱A 1B 1C 1ABC 的体积为V 2,则V 1∶V 2=________.解析 由题意可知点F 到面ABC 的距离与点A 1到面ABC 的距离之比为1∶2,S △ADE ∶S △ABC =1∶4. 因此V 1∶V 2=13AF ·S △AED 2AF ·S △ABC=1∶24.答案 1∶24。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1、集合A={z|z18=1},B={w|w18=1}都是复单位根的集合.C={zw|z∈A,w ∈B}也是复单位根的集合,问集合C中含有多少个元素?
例2、设U={1,2,3,…,1995},A U,且当x∈A时,19x A,求card(A)的最大值.
例3、设A={1,2,3,…,2n,2n+1}.B是A的一个子集,且B中的任意三个不同元素x,y,z都有x+y≠z,求card(B)的最大值.
例4、将与105互质的所有正整数从小到大排列成数列,求这个数的第1000项.
例5、设U={1,2,…,100},求最小的自然数n,使得U的每个n元子集都含有4个两两互质的数.
例1、设Sn表示正整数集合{1,2,…,n}的一切子集的元素之和(规定空集元素和为0),求S2003.
例2、一个集合含有10个互不相同的两位数.试证:这个集合必有两个公共元素的子集合,此两子集的各数之和相等.
例3、把含有12个元素的集合分成6个子集,每个子集都含有2个元素,有多少种分法?
例4、设S={a1,a2,…,a n}是整数集,其中n>1.对于S的非空子集A,定义P(A)为A的一切整数的乘积.设m(S)表示P(A)的算述平均数.这是A遍历S的一切非空子集.若m(S)=13,且有一切正整数am+1使得m(S∪{a n+1})=49,试确定a1,a2,…,a n及a n+1的值.
黄冈中学竞赛训练题高中数学(15)
例1、设集合M={x|0≤x≤11,x∈Z},集合F={(a,b,c,d)|a,b,c,d∈M},
映射f:F→Z.使得(a,b,c,d)ab-cd.已知(u,v,x,y)39,(u,y,x,v)66,求x,y,u,v的值.
例2、已知集合求一个A与B的一一对应f,并写出其逆映射.
例3、设X={1,2,…,100},对X的任一非空子集M,M中的最大数与最小数的和称为M的特征,记得m(M).求X的所有非空子集的特征的平均数.
例4、把△ABC的各边n等分,过各分点分别作各边的平行线,得到一些由三角形的边和这些平行线所组成的平行四边形,试计算这些平行四边形的个数.
例5、在一个6×6的棋盘上,已经摆好了一些1×2的骨牌,每一个骨牌都恰好覆盖两个相邻的格子.证明:如果还有14个格子没有被覆盖,则至少能再放进一步骨牌.。
