专题一含绝对值不等式的解法(含答案)
含绝对值不等式的解法

形如|x+m|±|x+n|<(或>)x+p的不等式的解法
例5 解不等式|x-1|+|2-x|>3+x.
【解】 原不等式变为|x-1|+|x-2|>3+x, 当x≥2时,原不等式变为x-1+x-2>3+x, 即x>6,∴x>6; 当1≤x<2时,原不等式变为x-1-(x-2)>3 +x, 即x<-2, ∴x∈∅;
即|x-4|+|x-3|≥1.
∴当a>1时,不等式有解.
变式训练 +4.
解不等式:|x-1|+|3x+5|≤4x
5 解:当 x<- 时,有-x+1-3x-5≤4x 3 +4, ∴8x≥-8.∴x≥-1, 此时无解. 5 当- ≤x<1 时,有 3 -x+1+3x+5≤4x+4, ∴2x≥2.∴x≥1, 此时无解.
当x≥1时,有
x-1+3x+5≤4x+4. ∴4≤4成立, ∴原不等式解集为{x|x≥1}.
5 当 x≥2 时,x-1+x-2>2,∴x> . 2 1 5 综上,原不等式解集为{x|x< 或 x> }. 2 2 法二:设 y1=|x-1|+|x-2|,y2=2.
-2x+3 ∴y1=1 1≤x<2 2x-3 x≥2
x<1 .
其图象如图.
1 5 ∴原不等式的解集为{x|x< 或 x> }. 2 2
a|≥3},且A∪B=R,求a的取值范围.
【思路点拨】 化简两个集合,求出解集形 式,通过两解集区间端点的关系求a.
【解】 ∵A={x||2-x|<5}={x||x-2|<5}= {x|-5<x-2<5}={x|-3<x<7};
01绝对值不等式(含经典例题+答案)

绝对值不等式一、绝对值三角不等式1.定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.2.定理2:如果a,b,c是实数,则|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.二、绝对值不等式的解法(1)|a x+b|≤c⇔-c≤a x+b≤c ;(2)|a x+b|≥c⇔a x+b≥c或a x+b≤-c .3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.二、绝对值不等式的解法(1)|a x+b|≤c⇔-c≤ax+b≤c ;(2)|a x+b|≥c⇔ax+b≥c或ax+b≤-c .3.|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.1.不等式|a|-|b|≤|a+b|≤|a|+|b|,右侧“=”成立的条件是ab≥0,左侧“=”成立的条件是ab≤0且|a|≥|b|;不等式|a|-|b|≤|a-b|≤|a|+|b|,右侧“=”成立的条件是ab≤0,左侧“=”成立的条件是ab≥0且|a|≥|b|.2.|x-a|+|x-b|≥c表示到数轴上点A(a),B(b)距离之和大于或等于c的所有点,只要在数轴上确定出具有上述特点的点的位置,就可以得出不等式的解.例4:若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a的取值范围是________.解:由于|x+1|+|x-2|≥|(x+1)-(x-2)|=3,所以只需a≤3即可.若本题条件变为“∃x∈R使不等式|x+1|+|x-2|<a成立为假命题”,求a的范围.解:由条件知其等价命题为对∀x∈R,|x+1|+|x-2|≥a恒成立,故a≤(|x+1|+|x-2|)min,又|x+1|+|x-2|≥|(x+1)-(x-2)|=3,∴a≤3.例5:不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是________.解:由绝对值的几何意义知:|x-4|+|x+5|≥9,则log3(|x-4|+|x+5|)≥2所以要使不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则需a<2.例6:某地街道呈现东——西,南——北向的网络状,相邻街距都为1,两街道相交的点称为格点.若以相互垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点,请确定一个格点(除零售点外)________为发行站,使6个零售点沿街道到发行站之间的路程的和最短.解:设格点(x,y)(其中x,y∈Z)为发行站,使6个零售点沿街道到发行站之间的路程的和最短,即使(|x+2|+|y-2|+(|x-3|+|y-1|)+(|x-3|+|y-4|)+(|x+2|+|y-3|)+(|x-4|+|y-5|)+(|x-6|+|y-6|)=[(|x+2|+|x-6|)+(|x+2|+|x-4|)+2|x-3|]+[|y-1|+|y-2|+|y-3|+|y-4|+|y-5|+|y-6|]取得最小值的格点(x,y)(其中x,y∈Z).注意到[(|x+2|+|x-6|)+(|x+2|+|x-4|) +2|x-3|]≥|(x+2)-(x-6)|+|(x+2)-(x-4)|+0=14,当且仅当x=3取等号;|y-1|+|y-2|+|y-3|+|y-4|+|y-5|+|y-6|=(|y-1|+|y-6|)+(|y-2|+|y-5|+(|y-3|+|y-4|)≥|(y-1)-(y-6)|+|(y-2)-(y-5)|+|(y-3)-(y-4)|=9,当且仅当y=3或y=4时取等号.因此,应确定格点(3,3)或(3,4)为发行站.又所求格点不能是零售点,所以应确定格点(3,3)为发行站.1.对绝对值三角不等式定理|a|-|b|≤|a±b|≤|a|+|b|中等号成立的条件要深刻理解,特别是用此定理求函数的最值时.2.该定理可以强化为:||a|-|b||≤|a±b|≤|a|+|b|,它经常用于证明含绝对值的不等式.3.对于求y=|x-a|+|x-b|或y=|x+a|-|x-b|型的最值问题利用绝对值三角不等式更简洁、方便.例7:设函数f(x)=|x-a|+3x,其中a>0.(1)当a=1时,求不等式f(x)≥3x+2的解集;(2)若不等式f(x)≤0的例9:已知关于x的不等式|2x+1|+|x-3|>2a-32恒成立,求实数a的取值范围.y =⎩⎪⎨⎪⎧ -3x +2,x <-12,x +4,-12≤x <3,3x -2,x ≥3,∴当x =-12时,y =|2x +1|+|x -3|取最小值72,∴72>2a -32,即得a <52. 例10:已知f (x )=1+x 2,a ≠b ,求证:|f (a )-f (b )|<|a -b |.解:∵|f (a )-f (b )|=|1+a 2-1+b 2|=|a 2-b 2|1+a 2+1+b 2=|a -b ||a +b |1+a 2+1+b 2, 又|a +b |≤|a |+|b |=a 2+b 2<1+a 2+1+b 2,∴|a +b |1+a 2+1+b 2<1.∵a ≠b ,∴|a -b |>0.∴|f (a )-f (b )|<|a -b |.例11:已知a ,b ∈R 且a ≠0,求证:|a |2|a |≥|a |2-|b |2. 证明:①若|a |>|b |,则左边=|a +b |·|a -b |2|a |=|a +b |·|a -b ||a +b +a -b |≥|a +b |·|a -b ||a +b |+|a -b |=11|a +b |+1|a -b |. ∵1|a +b |≤1|a |-|b |,1|a -b |≤1|a |-|b |,∴1|a +b |+1|a -b |≤2|a |-|b |.∴左边≥|a |-|b |2=右边,∴原不等式成立. ②若|a|=|b|,则a 2=b 2,左边=0=右边,∴原不等式成立.③若|a|<|b|,则左边>0,右边<0,原不等式显然成立.综上可知原不等式成立.证明:|f(x)-f(a)|=|x 2-x +43-a 2+a -43|=|(x -a)(x +a -1)|=|x -a|·|x +a -1|.∵|x -a|<1, ∴|x|-|a|≤|x -a|<1.∴|x|<|a|+1.∴|f(x)-f(a)|=|x -a|·|x +a -1|<|x +a -1|≤|x|+|a|+1<2(|a|+1). 例13:已知函数f (x )=log 2(|x -1|+|x -5|-a ).(1)当a =2时,求函数f (x )的最小值;(2)当函数f (x )的定义域为R 时,求实数a 的取值范围.解:函数的定义域满足|x -1|+|x -5|-a >0,即|x -1|+|x -5|>a .(1)当a =2时,f (x )=log 2(|x -1|+|x -5|-2),设g (x )=|x -1|+|x -5|,则g (x )=|x -1|+|x -5|=⎩⎪⎨⎪⎧ 2x -6,x ≥5,4,1<x <5,6-2x ,x ≤1,g (x )min =4,f (x )min =log 2(4-2)=1.(2)由(1)知,g (x )=|x -1|+|x -5|的最小值为4,|x -1|+|x -5|-a >0,∴a <4.∴a 的取值范围是(-∞,4). x -4|-|x -2|>1.解:(1)f (x )=⎩⎪⎨⎪⎧ -2, x >4,-2x +6, 2≤x ≤4,2, x <2.则函数y =f (x )的图像如图所示.(2)由函数y =f (x )的图像容易求得不等式|x -4|-|x -2|>1的解集为5,2⎛⎫-∞ ⎪⎝⎭。
6.5 含绝对值的不等式

|f(2)|=|4a+2b+c|=|3f(1)+f(-1)-3f(0)|≤3|f(1)|+|f(-1)|+3|f(0)|≤7. = + + = + - - + - + 此与f(2)> > 此与 矛盾. 矛盾.
变式3.已知 = 定义在区间[0,1]上,x1,x2∈[0,1],且x1≠x2, 变式 已知f(x)=x2-x+c定义在区间 已知 + 定义在区间 上 , 证明: 证明:(1)f(0)=f(1);(2)|f(x2)-f(x1)|<|x1-x2|; = ; - ; (3)|f(x2)-f(x1)|< - ;(4)|f(x2)-f(x1)|≤ - .
上恒成立, 故|f(x)-g(x)|≤1在x∈[2,3]上恒成立,从而两函数是接近的. - 在 ∈ 上恒成立 从而两函数是接近的. 答案: 答案:B
2.不等式1<|x+1|<3的解集为 .不等式 < + < 的解集为 的解集为( A.(0,2) . C.(-4,0) .-
)
B.(-2,0)∪(2,4) .- ∪ D.(-4,-2)∪(0,2) .- , ∪ 或 0<x<2或-4<x<- ,故选 项. <-2,故选D项 < < 或 < <-
(3)不妨设 2>x1,由(2)知|f(x2)-f(x1)|<x2-x1.① 不妨设x 不妨设 知 - ① 而由(1)知 = 而由 知f(0)=f(1),从而 2)-f(x1)|=|f(x2)-f(1)+f(0)-f(x1)| ,从而|f(x - = - + - ≤|f(x2)-f(1)|+|f(0)-f(x1)|<|1-x2|+|x1|=1-x2+x1② - + - - + = - ①+②得2|f(x2)-f(x1)|<1,即|f(x2)-f(x1)|< . - , - (4)|f(x2)-f(x1)|≤f(x)最大-f(x)最小=f(0)-f( )= - - = .
绝对值不等式的解法

综上,原不等式解集为{x|x<12或 x>25}
解不等式|x-1|+|x-2ห้องสมุดไป่ตู้>2.
法二:设 y1=|x-1|+|x-2|,y2=2.
-2x+3 ∴y1=1 1≤x<2
2x-3 x≥2
其图象如图.
x<1 .
∴原不等式的解集为{x|x<12或 x>52}.
即x2-3x+1<5. ∴x-∈1R<x,<4, 即-1<x<4. ∴原不等式的解集为{x|-1<x<4}.
变式训练1 解不等式|2x-1|<2-3x.
解:原不等式等价为 3x-2<2x-1<2-3x, 即22xx- -11<>23- x-3x2, ,
5x<3, 得x<1,
原不等式解集为{x|x<35}.
解不等式|x-1|+|x-2|>2.
【解】 法一:令 x-1=0,∴x=1. 令 x-2=0,∴x=2. ∴当 x<1 时,原不等式可化为
1-x+2-x>2,∴x<12,
∴原不等式解集为
1 x<2.
当 1≤x<2 时,原不等式可化为 x-1+2-x>2 不成立.
当 x≥2 时,x-1+x-2>2,∴x>25.
类型 二含多个绝对值不等式的解法 【典型例题】 1.不等式|x-1|>|x-2|的解集为______.
【解析】 1.|x-1|>|x-2|⇔(x-1)2>(x-2)2
x2-2x 1>x2-4x 4 2x>3 x>3 , 2
所以原不等式的解集为 {x | x>3}.
2
答案: ( 3, )
高中数学第一章不等关系与基本不等式1.2含有绝对值的

【做一做3】 解不等式|2x-5|-|x+1|<2.
分析:利用零点分区间法解题.
解:令 2x-5=0,得 x= 5 . 令x+1=0,得 x=-1.
2
(1)当 x≤-1 时,原不等式等价于-(2x-5)+(x+1)<2,
即-x+6<2,即 x>4,无解.
(2)当-1<x<
5 2
时,原不等式等价于-(2x-5)-(x+1)<2,
题型一 题型二 题型三
解法一:(几何法)如图,设数轴上与-2,1对应的点分别是A,B,则A,B 两点的距离是3,因此区间[-2,1]上的数都不是原不等式的解.为了求 出不等式的解,关键要在数轴上找出与点A,B的距离之和为5的点. 将点A向左移动1个单位到点A1,这时有|A1A|+|A1B|=5;
同理,将点B向右移动1个单位到点B1,这时也有|B1A|+|B1B|=5. 从数轴上可以看到,点A1与B1之间的任何点到点A,B的距离之和 都小于5;点A1的左边或点B1的右边的任何点到点A,B的距离之和都 大于5. 所以,原不等式的解集是(-∞,-3]∪[2,+∞).
2.2 绝对值不等式的解法
1.会用数轴上的点表示绝对值不等式的范围. 2.会解|ax+b|≤c,|ax+b|≥c,|x-a|+|x-b|≥c和|x-a|+|x-b|≤c四种类 型的绝对值不等式.
1.(1)解绝对值不等式的主要依据 解含绝对值的不等式的主要依据为绝对值的定义、绝对值的几 何意义及不等式的性质. (2)绝对值不等式的解法
【做一做1】 解下列绝对值不等式: (1)|x|<3;(2)|x|>4.
含绝对值不等式的解法1

方法一:等价于 不等式组
| ax b | n | ax b | m
方法二:几何意义
-m
-n 0 n
m
n ax b m,或 m ax b n
推广 a f(x) b a f(x) b或-b f(x) a
题型二:不等式n<| ax + b | <m (m>n>0) 的解集
∴原不等式的解集为{x | x<-2或x>-1}.
解题反思:
1、采用了整体换元。
2、归纳型如(a>0)
| f(x)|<a, |f(x)|>a 不 等式的解法。
| f(x)|<a | f(x)|>a
-a<f(x)<a
f(x)<-a或 f(x)>a
变式例题:型如 | f(x)|<a, |f(x)|>a的不等式中
题型四:含多个绝对值不等式的解法
练习4 解不等式 x+1 - x-3 2
解不等式
x2 x3 7
2x 4 3x 3 7
3.解不等式:| x 2 || x 1| 3
x 2
三、例题讲解
① -1 ② 3 ③
例2 解不等式|x +1| + |3-x| >2 + x.
解析原不等式变形为| X +1| + |X -3| > 2 + X.
不等式解集为 x x≥-1
推广 f x g x f x2 g x2
题型三:不等式 的解集|f(x)|> |g(x)| 练习3 解不等式 | x 2 || x 1|
四、练习
2.解不等式 x 9 x 1
解: x 9 x 1
x 92 x 12
高考数学一轮复习专题训练—绝对值不等式
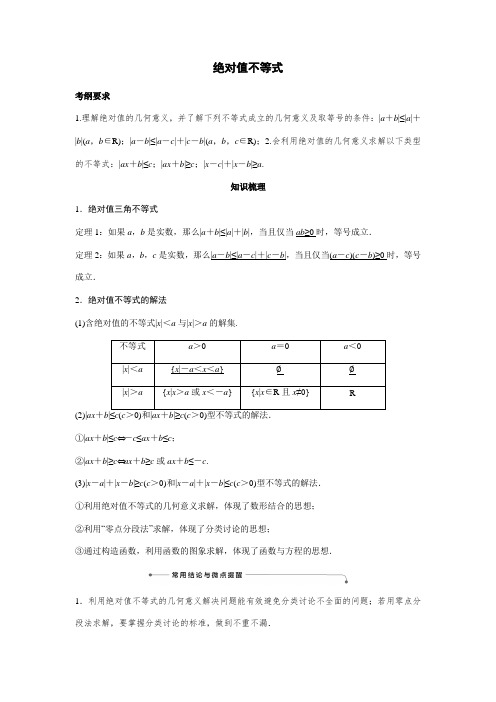
绝对值不等式考纲要求1.理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:|a+b|≤|a|+|b|(a,b∈R);|a-b|≤|a-c|+|c-b|(a,b,c∈R);2.会利用绝对值的几何意义求解以下类型的不等式:|ax+b|≤c;|ax+b|≥c;|x-c|+|x-b|≥a.知识梳理1.绝对值三角不等式定理1:如果a,b是实数,那么|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.定理2:如果a,b,c是实数,那么|a-b|≤|a-c|+|c-b|,当且仅当(a-c)(c-b)≥0时,等号成立.2.绝对值不等式的解法(1)含绝对值的不等式|x|<a与|x|>a的解集.不等式a>0a=0a<0|x|<a {x|-a<x<a}∅∅|x|>a {x|x>a或x<-a}{x|x∈R且x≠0}R(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法.①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.(3)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法.①利用绝对值不等式的几何意义求解,体现了数形结合的思想;②利用“零点分段法”求解,体现了分类讨论的思想;③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.1.利用绝对值不等式的几何意义解决问题能有效避免分类讨论不全面的问题;若用零点分段法求解,要掌握分类讨论的标准,做到不重不漏.2.绝对值三角不等式|a±b|≤|a|+|b|,从左到右是一个放大过程,从右到左是缩小过程,证明不等式可以直接用,也可利用它消去变量求最值.诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)若|x|>c的解集为R,则c≤0.()(2)不等式|x-1|+|x+2|<2的解集为∅.()(3)对|a+b|≥|a|-|b|当且仅当a>b>0时等号成立.()(4)对|a|-|b|≤|a-b|当且仅当|a|≥|b|时等号成立.()(5)对|a-b|≤|a|+|b|当且仅当ab≤0时等号成立.()答案(1)×(2)√(3)×(4)×(5)√2.不等式|x-1|-|x-5|<2的解集是()A.(-∞,4) B.(-∞,1) C.(1,4) D.(1,5)答案 A解析①当x≤1时,原不等式可化为1-x-(5-x)<2,∴-4<2,不等式恒成立,∴x≤1.②当1<x<5时,原不等式可化为x-1-(5-x)<2,∴x<4,∴1<x<4,③当x≥5时,原不等式可化为x-1-(x-5)<2,该不等式不成立.综上,原不等式的解集为(-∞,4).3.若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是________.答案(-∞,-3]∪[3,+∞)解析由于|x+1|+|x-2|≥|(x+1)-(x-2)|=3,∴|x+1|+|x-2|的最小值为3,要使原不等式有解,只需|a|≥3,即a≥3或a≤-3.4.若不等式|kx -4|≤2的解集为{x |1≤x ≤3},则实数k =________. 答案 2解析 因为|kx -4|≤2,所以-2≤kx -4≤2,所以2≤kx ≤6.因为不等式的解集为{x |1≤x ≤3},所以k =2.5.(2021·天津联考)若对任意的x ∈R ,不等式|x -1|-|x +2|≤|2a -1|恒成立,则实数a 的取值范围为________.答案 (-∞,-1]∪[2,+∞)解析 ∵y =|x -1|-|x +2|≤|(x -1)-(x +2)|=3, ∴要使|x -1|-|x +2|≤|2a -1|恒成立, 则|2a -1|≥3,2a -1≥3或2a -1≤-3, 即a ≥2或a ≤-1,∴实数a 的取值范围是(-∞,-1]∪[2,+∞). 6.(2021·郑州质量预测)已知函数f (x )=|x +1|-a |x -1|. (1)当a =-2时,解不等式f (x )>5; (2)若f (x )≤a |x +3|恒成立,求a 的最小值. 解 (1)当a =-2时,f (x )=⎩⎪⎨⎪⎧1-3x ,x ≤-1,-x +3,-1<x ≤1,3x -1,x >1.当x ≤-1时,由1-3x >5,得x <-43;当-1<x ≤1时,无解;当x >1时,由3x -1>5,得x >2. 故f (x )>5的解集为⎝⎛⎭⎫-∞,-43∪(2,+∞). (2)由f (x )≤a |x +3|得a ≥|x +1||x -1|+|x +3|,由|x -1|+|x +3|≥2|x +1|, 得|x +1||x -1|+|x +3|≤12,故a ≥12(当且仅当x ≥1或x ≤-3时等号成立),故a 的最小值为12.考点一 绝对值不等式的解法【例1】 (2020·全国Ⅰ卷)已知函数f (x )=|3x +1|-2|x -1|.(1)画出y =f (x )的图象; (2)求不等式f (x )>f (x +1)的解集.解 (1)由题设知f (x )=⎩⎪⎨⎪⎧-x -3,x ≤-13,5x -1,-13<x ≤1,x +3,x >1.画出y =f (x )的图象如图(1)所示.图(1)(2)函数y =f (x )的图象向左平移1个单位长度后得到函数y =f (x +1)的图象,如图(2)所示.图(2)易得y =f (x )的图象与y =f (x +1)的图象的交点坐标为⎝⎛⎭⎫-76,-116. 由图象可知,当且仅当x <-76时,y =f (x )的图象在y =f (x +1)的图象上方. 故不等式f (x )>f (x +1)的解集为⎝⎛⎭⎫-∞,-76. 【例2】 (2021·驻马店联考)已知函数f (x )=|x +a |+|2x -1|(a ∈R). (1)当a =-1时,求不等式f (x )≥2的解集; (2)若f (x )≤2x 的解集包含⎣⎡⎦⎤12,34,求a 的取值范围.解 (1)当a =-1时,不等式f (x )≥2可化为|x -1|+|2x -1|≥2, 当x ≤12时,不等式为1-x +1-2x ≥2,解得x ≤0;当12<x <1时,不等式为1-x +2x -1≥2,无解; 当x ≥1时,不等式为x -1+2x -1≥2,解得x ≥43.综上,原不等式的解集为(-∞,0]∪⎣⎡⎭⎫43,+∞.(2)因为f (x )≤2x 的解集包含⎣⎡⎦⎤12,34,所以不等式可化为|x +a |+2x -1≤2x ,即|x +a |≤1.解得-a -1≤x ≤-a +1,由题意知⎩⎨⎧-a +1≥34,-a -1≤12,解得-32≤a ≤14.所以实数a 的取值范围是⎣⎡⎦⎤-32,14. 感悟升华 1.用零点分段法解绝对值不等式的步骤(1)求零点;(2)划区间、去绝对值符号;(3)分别解去掉绝对值的不等式;(4)取每个结果的并集,注意在分段时不要遗漏区间的端点值.2.含绝对值的函数本质上是分段函数,绝对值不等式可利用分段函数的图象的几何直观性求解,体现了数形结合的思想.【训练1】 (2019·全国Ⅱ卷)已知f (x )=|x -a |x +|x -2|(x -a ). (1)当a =1时,求不等式f (x )<0的解集; (2)若x ∈(-∞,1)时,f (x )<0,求a 的取值范围. 解 (1)当a =1时,f (x )=|x -1|x +|x -2|(x -1). 当x <1时,f (x )=-2(x -1)2<0; 当x ≥1时,显然f (x )≥0.所以,不等式f (x )<0的解集为(-∞,1).(2)当a <1时,若a ≤x <1,则f (x )=(x -a )x +(2-x )(x -a )=2(x -a )≥0,不合题意;所以a ≥1, 当a ≥1,x ∈(-∞,1)时,f (x )=(a -x )x +(2-x )(x -a )=2(a -x )(x -1)<0. 所以,a 的取值范围是[1,+∞). 考点二 绝对值不等式性质的应用【例3】 设a >0,|x -1|<a 3,|y -2|<a3,求证:|2x +y -4|<a .证明 由|x -1|<a 3可得|2x -2|<2a 3,|2x +y -4|≤|2x -2|+|y -2|<2a 3+a3=a .【例4】 若f (x )=⎪⎪⎪⎪3x +1a +3|x -a |的最小值为4,求a 的值. 解 因为f (x )=⎪⎪⎪⎪3x +1a +3|x -a |≥⎪⎪⎪⎪⎝⎛⎭⎫3x +1a -3x -3a =⎪⎪⎪⎪1a +3a ,由⎪⎪⎪⎪1a +3a =4得a =±1或a =±13.感悟升华 1.求含绝对值的函数最值时,常用的方法有三种: (1)利用绝对值的几何意义.(2)利用绝对值三角不等式,即|a |+|b |≥|a ±b |≥|a |-|b |. (3)利用零点分区间法.2.含绝对值不等式的证明中,关键是绝对值三角不等式的活用. 【训练2】 设函数f (x )=x 2-x -15,且|x -a |<1. (1)解不等式|f (x )|>5;(2)求证:|f (x )-f (a )|<2(|a |+1).(1)解 因为|x 2-x -15|>5,所以x 2-x -15<-5或x 2-x -15>5,即x 2-x -10<0或x 2-x -20>0,解得1-412<x <1+412或x <-4或x >5,所以不等式|f (x )|>5的解集为⎩⎨⎧⎭⎬⎫x |x <-4或1-412<x <1+412或x >5.(2)证明 因为|x -a |<1,所以|f (x )-f (a )|=|(x 2-x -15)-(a 2-a -15)|=|(x -a )(x +a -1)|=|x -a |·|x +a -1|<1·|x +a -1|=|x -a +2a -1|≤|x -a |+|2a -1|<1+|2a -1|≤1+|2a |+1=2(|a |+1),即|f (x )-f (a )|<2(|a |+1). 考点三 绝对值不等式的综合应用 角度1 绝对值不等式恒成立问题【例5】 (2021·陇南二诊)已知a ≠0,函数f (x )=|ax -1|,g (x )=|ax +2|. (1)若f (x )<g (x ),求x 的取值范围;(2)若f (x )+g (x )≥|2×10a -7|对x ∈R 恒成立,求a 的最大值与最小值之和. 解 (1)因为f (x )<g (x ), 所以|ax -1|<|ax +2|,两边同时平方得a 2x 2-2ax +1<a 2x 2+4ax +4, 即6ax >-3,当a >0时,x >-12a ,即x 的取值范围是⎝⎛⎭⎫-12a ,+∞;当a <0时,x <-12a ,即x 的取值范围是⎝⎛⎭⎫-∞,-12a . (2)因为f (x )+g (x )=|ax -1|+|ax +2|≥|(ax -1)-(ax +2)|=3, 所以f (x )+g (x )的最小值为3,所以|2×10a -7|≤3,则-3≤2×10a -7≤3, 解得lg 2≤a ≤lg 5,故a 的最大值与最小值之和为lg 2+lg 5=lg 10=1. 角度2 绝对值不等式能成立问题【例6】 (2021·东北三省三校联考)已知函数f (x )=|2x +a |+1. (1)当a =2时,解不等式f (x )+x <2;(2)若存在a ∈⎣⎡⎦⎤-13,1时,使不等式f (x )≥b +|2x +a 2|的解集非空,求b 的取值范围. 解 (1)当a =2时,函数f (x )=|2x +2|+1, 不等式f (x )+x <2化为|2x +2|<1-x . 当1-x ≤0时,即x ≥1时,该不等式无解. 当1-x >0时,原不等式化为x -1<2x +2<1-x . 解之得-3<x <-13.综上,原不等式的解集为⎩⎨⎧⎭⎬⎫x -3<x <-13.(2)由f (x )≥b +|2x +a 2|, 得b ≤|2x +a |-|2x +a 2|+1,设g (x )=|2x +a |-|2x +a 2|+1,则不等式的解集非空,即不等式有解, 所以不等式等价于b ≤g (x )max .由g (x )≤|(2x +a )-(2x +a 2)|+1=|a 2-a |+1, 所以b ≤|a 2-a |+1.由题意知存在a ∈⎣⎡⎦⎤-13,1,使得上式成立,而函数h (a )=|a 2-a |+1在a ∈⎣⎡⎦⎤-13,1上的最大值为h ⎝⎛⎭⎫-13=139, 所以b ≤139,即b 的取值范围是⎝⎛⎦⎤-∞,139. 感悟升华 1.不等式恒成立问题,存在性问题都可以转化为最值问题解决.2.(1)在例6第(1)问,可作出函数y =|2x +2|与y =1-x 的图象,观察、计算边界,直观求得不等式的解集.(2)第(2)问把不等式解集非空,转化为求函数的最值.存在性问题转化方法:f (x )>a 有解⇔f (x )max >a ;f (x )<a 有解⇔f (x )min <a . 【训练3】 (2021·呼和浩特模拟)已知函数f (x )=|2x -a |+2|x +1|. (1)当a =1时,解关于x 的不等式f (x )≤6;(2)已知g (x )=|x -1|+2,若对任意x 1∈R ,都存在x 2∈R ,使得f (x 1)=g (x 2)成立,求实数a 的取值范围.解 (1)当a =1时,f (x )=|2x -1|+2|x +1|,则f (x )=⎩⎪⎨⎪⎧-4x -1,x <-1,3,-1≤x ≤12,4x +1,x >12.当x <-1时,由-4x -1≤6,得-74≤x <-1;当-1≤x ≤12时,f (x )≤6恒成立;当x >12时,由4x +1≤6,得12<x ≤54.综上,f (x )≤6的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-74≤x ≤54. (2)∵对任意x 1∈R ,都存在x 2∈R ,使得f (x 1)=g (x 2)成立, ∴{y |y =f (x )}⊆{y |y =g (x )}. 又f (x )=|2x -a |+2|x +1|≥|2x -a -(2x +2)| =|a +2|,g (x )=|x -1|+2≥2, ∴|a +2|≥2,解得a ≤-4或a ≥0,∴实数a 的取值范围是(-∞,-4]∪[0,+∞).1.(2020·全国Ⅱ卷)已知函数f (x )=|x -a 2|+|x -2a +1|. (1)当a =2时,求不等式f (x )≥4的解集; (2)若f (x )≥4,求a 的取值范围. 解 (1)当a =2时,f (x )=⎩⎪⎨⎪⎧7-2x ,x ≤3,1,3<x ≤4,2x -7,x >4.因此,不等式f (x )≥4的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤32或x ≥112. (2)因为f (x )=|x -a 2|+|x -2a +1|≥|a 2-2a +1|=(a -1)2, 故当(a -1)2≥4,即|a -1|≥2时,f (x )≥4. 所以当a ≥3或a ≤-1时,f (x )≥4.当-1<a <3时,f (a 2)=|a 2-2a +1|=(a -1)2<4. 所以a 的取值范围是(-∞,-1]∪[3,+∞). 2.已知f (x )=|x +1|-|ax -1|.(1)当a =1时,求不等式f (x )>1的解集;(2)若x ∈(0,1)时不等式f (x )>x 成立,求a 的取值范围. 解 (1)当a =1时,f (x )=|x +1|-|x -1|, 即f (x )=⎩⎪⎨⎪⎧-2,x ≤-1,2x ,-1<x <1,2,x ≥1.则当x ≥1时,f (x )=2>1恒成立,所以x ≥1; 当-1<x <1时,f (x )=2x >1, 所以12<x <1;当x ≤-1时,f (x )=-2<1.故不等式f (x )>1的解集为⎩⎨⎧⎭⎬⎫x |x >12. (2)当x ∈(0,1)时|x +1|-|ax -1|>x 成立等价于当x ∈(0,1)时|ax -1|<1成立. 若a ≤0,则当x ∈(0,1)时,|ax -1|≥1;若a >0,|ax -1|<1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪0<x <2a , 所以2a≥1,故0<a ≤2. 综上,a 的取值范围为(0,2].3.(2021·安徽江南十校模拟)已知函数f (x )=|x -1|+|x +2|.(1)求不等式f (x )<x +3的解集;(2)若不等式m -x 2-2x ≤f (x )在R 上恒成立,求实数m 的取值范围.解 (1)当x <-2时,f (x )<x +3可化为1-x -x -2<x +3,解得x >-43,无解; 当-2≤x ≤1时,f (x )<x +3可化为1-x +x +2<x +3,解得x >0,故0<x ≤1; 当x >1时,f (x )<x +3可化为x -1+x +2<x +3,解得x <2,故1<x <2. 综上可得,f (x )<x +3的解集为(0,2).(2)不等式m -x 2-2x ≤f (x )在R 上恒成立,可得m ≤x 2+2x +f (x )恒成立, 即m ≤[]x 2+2x +f x min .y =x 2+2x =(x +1)2-1的最小值为-1,此时x =-1.f (x )=|x -1|+|x +2|≥|x -1-x -2|=3,当且仅当-2≤x ≤1时,取得等号, 则[x 2+2x +f (x )]min =-1+3=2,所以m ≤2,即m 的取值范围是(-∞,2].4.已知f (x )=|x +1|+|x -m |.(1)若f (x )≥2,求m 的取值范围;(2)已知m >1,若∃x ∈(-1,1),f (x )≥x 2+mx +3成立,求m 的取值范围. 解 (1)因为f (x )=|x +1|+|x -m |≥|m +1|,所以只需|m +1|≥2,所以m +1≥2或m +1≤-2,解得m ≥1或m ≤-3,即m 的取值范围为(-∞,-3]∪[1,+∞).(2)因为m >1,所以当x ∈(-1,1)时,f (x )=m +1,所以f (x )≥x 2+mx +3,即m ≥x 2+mx +2,所以m (1-x )≥x 2+2,m ≥x 2+21-x , 令g (x )=x 2+21-x =1-x 2-21-x +31-x =(1-x )+31-x-2(-1<x <1). 因为-1<x <1,所以0<1-x <2,所以(1-x )+31-x≥23(当且仅当x =1-3时取“=”), 所以g (x )min =23-2,所以m ≥23-2.故实数m 的取值范围是[23-2,+∞).5.(2021·南昌摸底测试)已知f (x )=|2x +1|+|x -1|.(1)求不等式f (x )≥2的解集;(2)若f (x )≥a |x |恒成立,求a 的取值范围.解 (1)∵f (x )=|2x +1|+|x -1|≥2,①当x ≤-12时,⎩⎪⎨⎪⎧ x ≤-12,-2x -1-x +1≥2⇒x ≤-23; ②当-12<x <1时,⎩⎪⎨⎪⎧ -12<x <1,2x +1-x +1≥2⇒0≤x <1;③当x ≥1时,⎩⎪⎨⎪⎧x ≥1,2x +1+x -1≥2⇒x ≥1. 综上所述,f (x )≥2的解集为⎝⎛⎦⎤-∞,-23∪[0,+∞). (2)由题意知|2x +1|+|x -1|≥a |x |恒成立,①当x =0时,2≥a ·0恒成立,得a ∈R ;②当x ≠0时,|2x +1|+|x -1||x |=⎪⎪⎪⎪2+1x +⎪⎪⎪⎪1-1x ≥a 恒成立, 因为⎪⎪⎪⎪2+1x +⎪⎪⎪⎪1-1x ≥⎪⎪⎪⎪2+1x+1-1x =3,所以a ≤3. 综上所述,符合条件的实数a 的取值范围是(-∞,3].6.(2021·长春模拟)已知函数f (x )=|x +2|+|x -1|-a .(1)当a =4时,求函数f (x )的定义域;(2)若函数f (x )的定义域为R ,设a 的最大值为s ,当正数m ,n 满足12m +n +2m +3n =s 时,求3m +4n 的最小值.解 (1)当a =4时,|x +2|+|x -1|-4≥0,当x <-2时,-x -2-x +1-4≥0,解得x ≤-52; 当-2≤x ≤1时,x +2-x +1-4≥0,解得x ∈∅;当x >1时,x +2+x -1-4≥0,解得x ≥32. ∴函数f (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤-52或x ≥32. (2)∵函数f (x )的定义域为R ,∴|x +2|+|x -1|-a ≥0对任意的x ∈R 恒成立,∴a ≤|x +2|+|x -1|对任意的x ∈R 恒成立,又|x +2|+|x -1|≥|x +2-x +1|=3,∴a ≤3,∴s =3,∴12m +n +2m +3n=3,且m >0,n >0, ∴3m +4n =(2m +n )+(m +3n )=13[(2m +n )+(m +3n )]·⎝⎛⎭⎫12m +n +2m +3n =13⎣⎢⎡⎦⎥⎤3+22m +n m +3n +m +3n 2m +n ≥13(3+22)=1+223,当且仅当m =1+2215,n =3+215时取等号, ∴3m +4n 的最小值为1+223.。
含绝对值的不等式解法

解 | x a | 4 4 x a 4 A { x | a 4 x a 4} | x 2 | 3 x 2 3, 或x 2 3
B { x | x 1 ,或x 5}
a-4
-1
5
a+4
A
B R,
a 4 5 解得1 a 3 a的取值范围是 (1, 3) a 4 1
或x 0 x 3, 即 1 x 4
-1
0
3
4
原不等式的解集是{ x | 1 x 0, 或3 x 4}.
例3.设不等式 |x-a| < b的解集是 { x | -1<x< 2 }, 求实数a,b的值 . 解:若 b≤0,则 |x-a| < b的解集是 Φ, ∴ b>0.
2 x 1 3 x 5 }, 例5. 已知 A { x | | x 1 | a } , B { x | 5 x 2 3 x 6 且 A B , 求a的取值范围.
解:A { x | x 1 a, 或x 1 a}, B { x | 6 x 4} ,
| x a | b b x a b
ab x ab
∵ |x-a| < b的解集是 { x | -1<x< 2 }
a b 1 , 解得a 1 , b 3 . 2 2 a b 2
例4. 已知A={x| |x-a|<4},B={x| |x-2|>3} , 且 A∪B=R .求a的取值范围.
|x| c (c 0)的解集是 :{ x|x c 或 x c } .
由此可得: {x|-c <ax+b< c}; |ax+b|<c (c>0)的解集为: |ax+b|>c (c>0)的解集为: {x|ax+b>c ,或 ax+b<-c}.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三讲 含绝对值不等式与一元二次不等式一、知识点回顾1、绝对值的意义:(其几何意义是数轴的点A (a )离开原点的距离a OA =)()()()⎪⎩⎪⎨⎧<-=>=0,0,00,a a a a a a2、含有绝对值不等式的解法:(解绝对值不等式的关键在于去掉绝对值的符号) (1)定义法;(2)零点分段法:通常适用于含有两个及两个以上的绝对值符号的不等式; (3)平方法:通常适用于两端均为非负实数时(比如()()x g x f <);(4)图象法或数形结合法; (5)不等式同解变形原理:即()a x a a a x <<-⇔><0 ()a x a x a a x -<>⇔>>或0()c b ax c c c b ax <+<-⇔><+0 ()c b ax c b ax c c b ax -<+>+⇔>>+或0()()()()()x g x f x g x g x f <<-⇔< ()()()()()()x g x f x g x f x g x f <>⇔>或 ()()()()a x f b b x f a a b b x f a -<<-<<⇔>><<或03、不等式的解集都要用集合形式表示,不要使用不等式的形式。
4、二次函数、一元二次方程、一元两次不等式的联系。
(见P8)5、利用二次函数图象的直观性来研究一元二次方程根的性质和一元二次不等式解集及变化,以及含字母的有关问题的讨论,渗透数形结合思想。
6、解一元二次不等式的步骤:(1)将不等式化为标准形式()002≥>++c bx ax 或()002≤<++c bx ax (2)解方程02=++c bx ax(3)据二次函数c bx ax y ++=2的图象写出二次不等式的解集。
一、 基本解法与思想解含绝对值的不等式的基本思想是等价转化,即采用正确的方法去掉绝对值符号转化为不含绝对值的不等式来解,常用的方法有公式法、定义法、平方法。
(一)、公式法:即利用a x >与a x <的解集求解。
主要知识:1、绝对值的几何意义:x 是指数轴上点x 到原点的距离;21x x -是指数轴上1x ,2x 两点间的距离.。
2、a x >与a x <型的不等式的解法。
当0>a 时,不等式>x 的解集是{}a x a x x -<>或,不等式a x <的解集是{}a x a x <<-;当0<a 时,不等式a x >的解集是{}R x x ∈不等式a x <的解集是∅;3.c b ax >+与c b ax <+型的不等式的解法。
把 b ax + 看作一个整体时,可化为a x <与a x >型的不等式来求解。
当0>c 时,不等式c b ax >+的解集是{}c b ax c b ax x -<+>+或,不等式c b ax <+的解集是{}c b ax c x <+<-;当0<c 时,不等式c b ax >+的解集是{}R x x ∈不等式c bx a <+的解集是∅;例1 解不等式32<-x分析:这类题可直接利用上面的公式求解,这种解法还运用了整体思想,如把“2-x ” 看着一个整体。
答案为{}51<<-x x 。
(解略) (3)532<+<-x (2) 392+≤-x x(1)解:原不等式等价于032<-x ,所以不等式解集为⎭⎬⎫⎩⎨⎧>32x x(2)解:(1)法一:原不等式⎩⎨⎧+≤-≥-⇔390922x x x ①或⎩⎨⎧+≤-<-390922x x x ② 由①解得433≤≤-=x x 或,由②解得32<≤x ∴原不等式的解集是{}342-=≤≤x x x 或法二:原等式等价于39)3(2+≤-≤+-x x x ⎩⎨⎧≤≤-≥-≤⇔4323x x x 或423≤≤-=⇔x x 或∴原不等式的解集是{}342-=≤≤x x x 或法三:设)33,9221-≥+=-=x x y x y (,由392+=-x x 解得非曲直2,3,4321=-==x x x ,在同一坐标系下作出它们的图象,由图得使21y y ≤的x 的范围是433≤≤-=x x 或,∴原不等式的解集是{}342-=≤≤x x x 或评析:数形结合策略运用要解出两函数图象的交点。
(二)、定义法:即利用(0),0(0),(0).a a a a a a >⎧⎪==⎨⎪-<⎩去掉绝对值再解。
例2。
解不等式22x xx x >++。
分析:由绝对值的意义知,a a =⇔a ≥0,a a =-⇔a ≤0。
o -3 3 x9 y3解:原不等式等价于2xx +<0⇔x(x+2)<0⇔-2<x <0。
练习:x x 3232->-(1)解:原不等式等价于032<-x ,所以不等式解集为⎭⎬⎫⎩⎨⎧>32x x(三)、平方法:解()()f x g x >型不等式。
例3、解不等式123x x ->-。
解:原不等式⇔22(1)(23)x x ->-⇔22(23)(1)0x x ---<⇔(2x-3+x-1)(2x-3-x+1)<0⇔(3x-4)(x-2)<0 ⇔423x <<。
说明:求解中以平方后移项再用平方差公式分解因式为宜。
二、分类讨论法:即通过合理分类去绝对值后再求解。
例4 解不等式125x x -++<。
分析:由01=-x ,02=+x ,得1=x 和2=x 。
2-和1把实数集合分成三个区间,即2-<x ,12≤≤-x ,1>x ,按这三个区间可去绝对值,故可按这三个区间讨论。
解:当x <-2时,得2(1)(2)5x x x <-⎧⎨---+<⎩,解得:23-<<-x 当-2≤x ≤1时,得21,(1)(2)5x x x -≤≤⎧⎨--++<⎩,解得:12≤≤-x当1>x 时,得1,(1)(2) 5.x x x >⎧⎨-++<⎩ 解得:21<<x综上,原不等式的解集为{}23<<-x x 。
说明:(1)原不等式的解集应为各种情况的并集;(2)这种解法又叫“零点分区间法”,即通过令每一个绝对值为零求得零点,求解应注意边界值。
三、几何法:即转化为几何知识求解。
例5 对任何实数x ,若不等式12x x k +-->恒成立,则实数k 的取值范围为 ( )(A)k<3(B)k<-3(C)k ≤3(D)k ≤-3分析:设12y x x =+--,则原式对任意实数x 恒成立的充要条件是min k y <,于是题转化为求y 的最小值。
解:1x +、2x -的几何意义分别为数轴上点x 到-1和2的距离1x +-2x -的几何意义为数轴上点x 到-1与2的距离之差,如图可得其最小值为-3,故选(B )。
(3)分析:关键是去掉绝对值方法1:零点分段讨论法(利用绝对值的代数定义) ①当1-<x 时,01,03<+<-x x ∴1)1()3(<++--x x ∴ 4<1 φ∈⇒x ②当31<≤-x 时∴1)1()3(<+---x x ⇒21>x ,∴}321|{<<x x ③当3≥x 时1)1()3(<+--x x ⇒-4<1R x ∈⇒ ∴}3|{≥x x综上,原不等式的解集为}21|{>x x也可以这样写: 解:原不等式等价于①⎩⎨⎧<++---<1)1()3(1x x x 或②⎩⎨⎧<+---<≤-1)1()3(31x x x 或 ③⎩⎨⎧<+--≥1)1()3(3x x x ,解①的解集为φ,②的解集为{x|21<x<3},③的解集为{x|x ≥3},∴原不等式的解集为{x|x>21}方法2:数形结合从形的方面考虑,不等式|x-3|-|x+1|<1表示数轴上到3和-1两点的距离之差小于1的点x3O 12-1∴原不等式的解集为{x|x>21}变式:(1)若a x x >+++12恒成立,求实数a 的取值范围。
解:由几何意义可知,12+++x x 的最小值为1,所以实数a 的取值范围为()1,∞-。
(2)数轴上有三个点A 、B 、C ,坐标分别为-1,2,5,在数轴上找一点M ,使它到A 、B 、C 三点的距离之和最小。
解:设M (x ,0)则它到A 、B 、C 三点的距离之和()521-+-++=x x x x f即()⎪⎪⎩⎪⎪⎨⎧-<+-<≤-+-<≤+≥-=1,6321,852,45,63x x x x x x x x x f由图象可得:当()62min ==x f x 时四、典型题型1、解关于x 的不等式10832<-+x x解:原不等式等价于1083102<-+<-x x ,即⎩⎨⎧<-+->-+1083108322x x x x ⇒⎩⎨⎧<<--<->3621x x x 或 ∴ 原不等式的解集为)3,1()2,6(---2、解关于x 的不等式2321>-x 解:原不等式等价于⎪⎩⎪⎨⎧<-≠-2132032x x ⇒⎪⎩⎪⎨⎧<<≠474523x x 3、解关于x 的不等式212+<-x x解:原不等式可化为22)2()12(+<-x x ∴ 0)2()12(22<+--x x 即 0)13)(3(<+-x x解得:331<<-x∴ 原不等式的解集为)3,31(-4、解关于x 的不等式1212-<-m x )(R m ∈解:⑴ 当012≤-m 时,即21≤m ,因012≥-x ,故原不等式的解集是空集。
⑵ 当012>-m 时,即21>m ,原不等式等价于1212)12(-<-<--m x m解得:m x m <<-1综上,当21≤m 时,原不等式解集为空集;当21>m 时,不等式解集为{}m x m x <<-15、解关于x 的不等式1312++<--x x x解:当3-<x 时,得⎩⎨⎧++-<----<1)3()12(3x x x x ,无解当213≤≤-x ,得⎪⎩⎪⎨⎧++<---≤≤-13)12(213x x x x ,解得:2143≤<-x 当21>x 时,得⎪⎩⎪⎨⎧++<-->131221x x x x ,解得:21>x 综上所述,原不等式的解集为43(-,)216、解关于x 的不等式521≥++-x x (答案:),2[]3,(+∞--∞ ) 解:五、巩固练习1、设函数)2(,312)(-++-=f x x x f 则= ;若2)(≤x f ,则x 的取值范围是 .2、已知a ∈R ,若关于x 的方程2104x x a a ++-+=有实根,则a 的取值范围 是 .3、不等式121≥++x x 的实数解为 .4、解下列不等式 ⑴4321x x ->+; ⑵ |2||1|x x -<+; ⑶ |21||2|4x x ++->;⑷ 4|23|7x <-≤ ; ⑸ 241<--x ; ⑹ a a x <-2(a R ∈) 5、若不等式62<+ax 的解集为()1,2-,则实数a 等于 ( ).A 8 .B 2 .C 4- .D 8- 6、若x R ∈,则()()110x x -+>的解集是( ).A {}01x x ≤<.B {0x x <且1}x ≠-.C {}11x x -<< .D {1x x <且1}x ≠-7、()1对任意实数x ,|1||2|x x a ++->恒成立,则a 的取值范围是 ;()2对任意实数x ,|1||3|x x a --+<恒成立,则a 的取值范围是 ;()3若关于x 的不等式|4||3|x x a -++<的解集不是空集,则a 的取值范围是 ;8、不等式x x 3102≤-的解集为( ).A {}|210x x ≤≤ .B {}|25x x -≤≤ .C {}|25x x ≤≤ .D {}|105x x ≤≤ 9、解不等式:221>-+-x x10、方程x x x x x x 323222++=++的解集为 ,不等式xxx x ->-22的解集是 ; 12、不等式x 0)21(>-x 的解集是( ).A )21,(-∞ .B )21,0()0,( -∞ .C ),21(+∞ .D )21,0( 11、不等式3529x ≤-<的解集是.A ()(),27,-∞-+∞ .B []1,4 .C [][]2,14,7- .D (][)2,14,7-12、 已知不等式a x ≤-2)0(>a 的解集为{}c x R x <<-∈1|,求c a 2+的值13、解关于x 的不等式:①解关于x 的不等式31<-mx ;②a x <-+132)(R a ∈ 14、不等式1|1|3x <+<的解集为( )..A (0,2) .B (2,0)(2,4)- .C (4,0)- .D (4,2)(0,2)--15、 设集合{}22,A x x x R =-≤∈,{}21,2≤≤--==x x y y B ,则()R C A B 等于 ( ).A R .B {},0x x R x ∈≠ .C {}0 .D ∅ 16、不等式211x x --<的解集是 .17、设全集U R =,解关于x 的不等式: 110x a -+->()x R ∈(参考答案)1、 6 ; ∅ ;2、 ]4,0[3、)23,2()2,(----∞ 4、⑴ ⎭⎬⎫⎩⎨⎧><231x x x 或 ⑵ ⎭⎬⎫⎩⎨⎧>21x x ⑶ ⎭⎬⎫⎩⎨⎧>-<121x x x 或⑷ ⎭⎬⎫⎩⎨⎧≤<-<≤-527212x x x 或 ⑸ {}7315<<-<<-x x x 或 ⑹ 当0>a 时,{}a x a x 22<<-;当0≤a 时,不等式的解集为∅ 5、C 6、D 7、⑴ 3<a ; ⑵ 4>a ; ⑶ 7>a ; 8、C 9、⎭⎬⎫⎩⎨⎧><2521x a x x 或 10、{}023>≤<-x x x 或;{}02<>x x x 或11、D 12、 1513、① 当0=m 时,R x ∈;当0>m 时,m x m 42<<-;当0<m 时,mx m 24-<< ② 当01>+a ,即1->a 时,不等式的解集为⎭⎬⎫⎩⎨⎧-<<-122a x a x ;当01≤+a ,即1-≤a 时,不等式的解集为∅; 14、D 15、B 16、0(,)217、当01>-a ,即1<a 时,不等式的解集为{}a x a x x -><2或;当01=-a ,即1=a 时,不等式的解集为{}1≠x x ; 当01<-a ,即1>a 时,不等式的解集为R ;。
