金属学与热处理第2版第五章
金属学与热处理第2版教学作者崔忠圻覃耀春主编金属学与热处理(全套课件齐)讲述

10
第十一章 工 业 用 钢
第十二章 铸 铁
6
第十三章 有色金属及合金
退出
7
编
辑:崔忠圻 覃耀春 制 作:张 宇 技术支持:路庆福
机械工业出版社高职教育分社 机械工业出版社音像分社 联合制作
8
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。 9
1
2
主 编:
哈尔滨工业大学 崔忠圻 覃耀春
3
第一章 金属的晶体结构 第三章 二元合金的相结构 与结晶
第二章 纯金属的结晶
第四章 铁 碳 合 金
4
第五章 三元合金相图 第七章 金属及合金的回复与 再结晶
第六章 金属及合金的塑性变形 与断裂
第八章 扩 散
5
第九章 钢的热处理原理
第十章 钢的热处理工艺
(完整word版)金属学与热处理(哈尔滨工业大学_第二版)课后习题答案
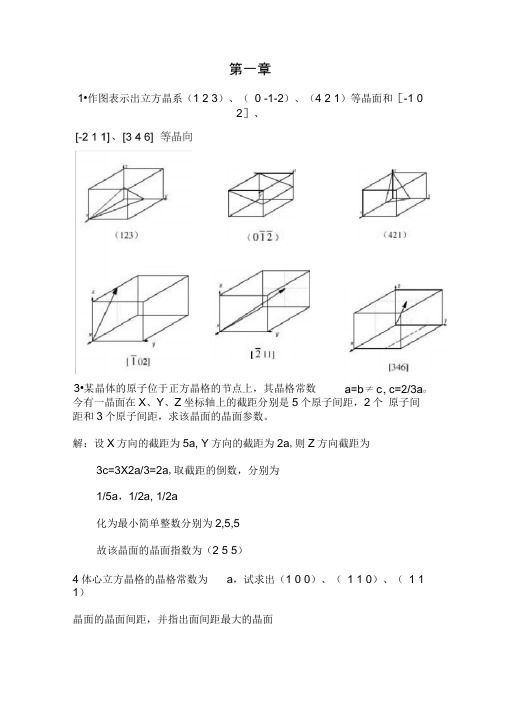
第一章1•作图表示出立方晶系(1 2 3)、(0 -1-2)、(4 2 1)等晶面和[-1 02]、3•某晶体的原子位于正方晶格的节点上,其晶格常数今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距,2个原子间距和3个原子间距,求该晶面的晶面参数。
解:设X方向的截距为5a, Y方向的截距为2a,则Z方向截距为3c=3X2a/3=2a,取截距的倒数,分别为1/5a,1/2a, 1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)4体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的晶面间距,并指出面间距最大的晶面解:(1 0 0)面间距为a/2, (1 1 0)面间距为"2a/2, (1 1 1)面间距为"3a/3三个晶面晶面中面间距最大的晶面为(1 1 0)7证明理想密排六方晶胞中的轴比c/a=1.633证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,成正四面体,如图所示贝卩OD=c/2,AB=BC=CA=CD=a因厶ABC是等边三角形,所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2有(CD)2=(OC)2+(1/2C)2,即I /T J(CU)(c)2- '3 2因此c/a=V8/3=1.6338•试证明面心立方晶格的八面体间隙半径为r=0.414R解:面心立方八面体间隙半径r=a/2-v2a/4=0.146a面心立方原子半径R二辺a/4,贝卩a=4R/\2,代入上式有R=0.146X4R/ V2=0.414R9. a )设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积膨胀。
b)经X射线测定,在912C时丫-Fe的晶格常数为0.3633nm, a -Fe的晶格常数为0.2892nm,当由丫-Fe转化为a -Fe时,求其体积膨胀,并与a)比较,说明其差别的原因。
金属学与热处理(哈尔滨工业大学 - 第二版)课后习题答案 - 附总

金属学与热处理(哈尔滨工业大学 - 第二版)课后习题答案 -附总第六章1. 试用多晶体的塑性变形过程说明金属晶粒越细强度越高、塑性越好的原因是什么?2.答:由 Hall-Petch 公式可知,屈服强度σs 与晶粒直径平方根的倒数 d v2呈线性关系。
在多晶体中,滑移能否从先塑性变形的晶粒转移到相邻晶粒主要取决于在已滑移晶粒晶界附近的位错塞积群所产生的应力集中能否激发相邻晶粒滑移系中的位错源,使其开动起来,从而进行协调性的多滑移。
由τ=nτ0知,塞积位错数目n越大,应力集中τ越大。
位错数目n与引起塞积的晶界到位错源的距离成正比。
晶粒越大,应力集中越大,晶粒小,应力集中小,在同样外加应力下,小晶粒需要在较大的外加应力下才能使相邻晶粒发生塑性变形。
在同样变形量下,晶粒细小,变形能分散在更多晶粒内进行,晶粒内部和晶界附近应变度相差较小,引起的应力集中减小,材料在断裂前能承受较大变形量,故具有较大的延伸率和断面收缩率。
另外,晶粒细小,晶界就曲折,不利于裂纹传播,在断裂过程中可吸收更多能量,表现出较高的韧性。
2.金属材料经塑性变形后为什么会保留残留内应力?研究这部分残留内应力有什么实际意义?金属材料经塑性变形后为什么会保留残留内应力?研究这部分残留内应力有什么实际意义?答:残余内应力存在的原因1)塑性变形使金属工件或材料各部分的变形不均匀,导致宏观变形不均匀; 2)塑性变形使晶粒或亚晶粒变形不均匀,导致微观内应力;3)塑性变形使金属内部产生大量的位错或空位,使点阵中的一部分原子偏离其平衡位置,导致点阵畸变内应力。
实际意义:可以控制材料或工件的变形、开裂、应力腐蚀;可以利用残留应力提高工件的使用寿命。
3.何谓脆性断裂和塑性断裂,若在材料中存在裂纹时,试述裂纹对脆性材料和塑性材料断裂过程中的影响。
答:塑性断裂又称为延性断裂,断裂前发生大量的宏观塑性变形,断裂时承受的工程应力大于材料的屈服强度。
在塑性和韧性好的金属中,通常以穿晶方式发生塑性断裂,在断口附近会观察到大龄的塑性变形痕迹,如缩颈。
《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]
![《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]](https://img.taocdn.com/s3/m/e4df0f3a3186bceb18e8bb02.png)
第一章金属的晶体结构之阿布丰王创作1-1 作图暗示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包含(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/2H(1 1 1)==√3a/6面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/4H(1 1 1)==√3a/3面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,将各原子中心相连接形成一个正四面体,如图所示:此时c/a=2OD/BC在正四面体中:AC=AB=BC=CD ,OC=2/3CE所以:OD2=CD2-OC2=BC2- OC2OC=2/3CE,OC2=4/9CE2,CE2=BC2-BE2=3/4BC2可得到OC2=1/3 BC2,OD2= BC2- OC2=2/3 BC2OD/BC=√6/3所以c/a=2OD/BC=2√6/3≈1-8 试证明面心立方晶格的八面体间隙半径r=0.414R,四面体间隙半径r=0.225R;体心立方晶格的八面体间隙半径:<1 0 0>晶向的r=0.154R,<1 1 0>晶向的r=0.633R,四面体间隙半径r=0.291R。
《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]
![《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]](https://img.taocdn.com/s3/m/b52838811a37f111f1855b79.png)
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/2H(1 1 0)==√3a/6H(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)H==√2a/4(1 1 0)==√3a/3H(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
《金属学与热处理》(第二版)课后习题参考答案

《金属学与热处理》(第二版)课后习题参考答案金属学与热处理第一章习题1.作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6] 等晶向3.某晶体的原子位于正方晶格的节点上,其晶格常数a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距,2个原子间距和3个原子间距,求该晶面的晶面参数。
解:设X方向的截距为5a,Y方向的截距为2a,则Z方向截距为3c=3X2a/3=2a,取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)4.体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的晶面间距,并指出面间距最大的晶面解:(1 0 0)面间距为a/2,(1 1 0)面间距为√2a/2,(1 1 1)面间距为√3a/3三个晶面晶面中面间距最大的晶面为(1 1 0)7.证明理想密排六方晶胞中的轴比c/a=1.633证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,成正四面体,如图所示则OD=c/2,AB=BC=CA=CD=a因△ABC是等边三角形,所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2则有(CD)2=(OC)2+(1/2c)2,即因此c/a=√8/3=1.6338.试证明面心立方晶格的八面体间隙半径为r=0.414R解:面心立方八面体间隙半径r=a/2-√2a/4=0.146a面心立方原子半径R=√2a/4,则a=4R/√2,代入上式有R=0.146X4R/√2=0.414R9.a)设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积膨胀。
b)经X射线测定,在912℃时γ-Fe的晶格常数为0.3633nm,α-Fe的晶格常数为0.2892nm,当由γ-Fe转化为α-Fe时,求其体积膨胀,并与a)比较,说明其差别的原因。
《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]之欧阳地创编
第一章金属的晶体结构时间:2021.03.04 创作:欧阳地1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(42 1)等晶面和[-1 0 2]、[-2 1 1]、[34 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/2H(1 1 1)==√3a/6面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/4H(1 1 1)==√3a/3面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
金属学与热处理崔忠圻(第二版)课后答案完整版
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)==√2a/2H(1 1 0)H==√3a/6(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/4H(1 1 0)H==√3a/3(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,将各原子中心相连接形成一个正四面体,如图所示:此时c/a=2OD/BC在正四面体中:AC=AB=BC=CD ,OC=2/3CE所以:OD2=CD2-OC2=BC2- OC2OC=2/3CE,OC2=4/9CE2,CE2=BC2-BE2=3/4BC2可得到OC2=1/3 BC2,OD2= BC2- OC2=2/3 BC2OD/BC=√6/3所以c/a=2OD/BC=2√6/3≈1-8 试证明面心立方晶格的八面体间隙半径r=,四面体间隙半径r=;体心立方晶格的八面体间隙半径:<1 0 0>晶向的r=,<1 1 0>晶向的r=,四面体间隙半径r=。
15年金属学与热处理第5章习题及思考题
1.概念:滑移:在外力作用下,晶体相邻二部分沿一定晶面、一定晶向彼此产生相对的平行滑动。
临界分切应力:使滑移系开动的最小分切应力。
软取向与硬取向:φ=45°时:取向因子可获得最大值1/2(cos λ·cos φ=cos(90°-φ)·cos φ),取向因子大,易产生滑移,软取向;φ或λ=90°时:取向因子为0,难滑移,硬取向。
多滑移:晶体的滑移在两组或者更多的滑移系上同时进行。
可促进加工硬化。
交滑移:多个滑移面同时沿一个滑移方向进行的滑移。
可降低脆性。
滑移系:一个滑移面和该面上的一个滑移方向组成滑移系。
孪生:晶体在切应力下其一部分沿一定的晶面和晶向相对于另一部分作均匀切变。
形变织构:金属塑性变形到很大程度(>70%)时,晶粒发生转动,各晶粒的位向趋于一致,这种有序化的结构。
加工硬化:随变形度增大,金属的强硬度显著增高而塑韧性明显下降的现象。
屈服效应:在拉伸的σ-ε曲线上,有明显的上、下屈服点及屈服平台的现象。
柯氏气团(柯垂尔气团):溶质原子在刃型位错周围聚集的现象,可阻碍位错运动。
形变时效:具有明显屈服效应的金属,在变形后于室温长期仃留或短时加热保温,引起屈服应力升高并出现明显屈服点的现象。
吕德斯带:具有屈服现象的试样从上屈服点出现直到屈服延伸结束,在试样表面看到由于不均匀变形而形成的表面皱褶带, 称为吕德斯带。
细晶强化:通过细化晶粒,增加晶界,提高材料强度的方法。
2.滑移的特点:参考解析:⑴发生在最密排晶面,滑移方向为最密排晶向;原因:密排面间原子面结合力最弱⑵只在切应力下发生,存在临界分切应力;⑶滑移两部分相对移动的距离是原子间距的整数倍,滑移后滑移面两边的晶体位向仍保持一致;⑷伴随晶体的转动和旋转,滑移面转向与外力平行方向,滑移方向旋向最大切应力方向;⑸随滑移加剧,存在多滑移和交滑移现象。
3.分别列举出BCC、FCC和HCP的滑移系:参考解析:BCC:滑移面{110},滑移方向〈111〉。
《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]
第一章金属的晶体结构1-1 作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包括(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H==a/2(1 0 0)==√2a/2H(1 1 0)==√3a/6H(1 1 1)面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:==a/2H(1 0 0)H==√2a/4(1 1 0)==√3a/3H(1 1 1)面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线法则和杠杆定律
直线法则和杠杆定律对于使用和加深理解三元 相图都很有用。在以后分析三元相图时,可以利用 以下规律: 1)当给定合金在一定温度下处于两相平衡状态 时,若其中一相的成分给定,则根据直线法则,另 一相的成分点必位于二已知成分点的延长线上。 2)若两个平衡相的成分点已知,合金的成分点 必然位于两个已知成分点的连线上。
第二节 三元系平衡相的定量法则
一、直线法则和杠杆定律
根据相律,二元合金两相平衡时,有一个自由度, 若温度恒定,则自由度为零。说明两个平衡相的成分不 变,其连接线的两个端点即为两平衡相的成分,这样就 可以应用杠杆定律计算两个平衡相的含量。对于三元合 金来说,根据相律,两相平衡时有两个自由度,若温度 恒定,还剩下一个自由度,说明两个相中只有一个相的 成分可以独立改变,而另一个相的成分则必须随之改变。 也就是说,两个平衡相的成分存在着一定的对应关系, 这个关系便是直线法则。所谓直线法则(共线法则)是 指三元合金在两相平衡时,合金的成分点和两个平衡相 的成分点,必定在同一条直线上。
一、成分三角形
三元合金的成分通常用三角形表示,这个三角 形叫做成分三角形或浓度三角形。常用的成分三角 形有等边三角形、直角三角形和等腰三角形,这里 主要介绍用等边三角形表示三元合金成分的方法。 取一等边三角形ABC,如图5-1所示。三角形的 三个顶点A、B、C分别表示三个组元,三角形的边AB、 BC、CA分别表示三个二元系A-B、B-C和C-A的成分。 三角形内的任一点则代表一定成分的三元合金。
图5-中具有特定意义的直线
(一)平行于三角形某一条边的直线 凡成分位于该线上的合金,它们所含的、由 这条边对应顶点所代表的组元的含量为一定值。 如成分位于GQ 线上的所有合金,B组元的含量都是 wB=AG %。 (二)通过三角形顶点的任一直线 凡成分位于该直线上的三元合金,它们所含 的、由另两个顶点所代表的两组元的量之比是恒 定的。
二、重 心 法 则
根据相律可知,某一三元合金处于三相平衡 时,其自由度为1,这表明,三个平衡相的成分是 依赖温度而变化的,当温度恒定时,则自由度为 零,三个平衡相的成分为确定值。显然,在三相 平衡时意味着存在三个两相平衡,由于两相平衡 时的连接线为直线,三条连接线必然会组成一个 三角形,称为连接三角形。
三、等温截面(水平截面)
等温截面又称水平截面,它表示三元系合金在某 一温度下的状态。图5-9b即表示ABC三元系在t1温度的 等温截面,它相当于在立体模型中插入一个t1温度的水 平面,该面与液相面和固相面分别交截于L1L2和S1S2 (图5-9a),将这两条线投影到成分三角形上,就得 到了图5-9b所示的等温截面图。
图5-2 有网格的成分三角形
成分三角形
反过来,若已知合金中三个组元的含量,欲求该 合金在成分三角形内的位置时,即可在三个边上代 表各组元成分的相应点,分别作其对边的平行线, 这些平行线的交点即为该合金的成分点。
二、在成分三角形中具有特定意义的直线
在成分三角形中, 有两条具有特定意义的 直线,如图5-3所示。
成分三角形
图5-1 等边三角形的几何特性
成分三角形
为了便于使用,在成分三 角形内常画出平行于成分坐标 的网格,如图5-2所示。为了 确定成分三角形中合金x的成 分,通过x点作A点对边BC的平 行线,截CA或AB边于55%处, 这就是合金中A组元的含量。 由x点作B点对边CA的平行线, 截AB边于20%处,这就是合金 中B组元的含量。同样可以确 定C组元的含量为25%。
重 心 法 则
在图5-6中,如由N成分的合金分解为α、β、 γ三个相,三个相的成分点为D、E、F,则合金N的 成分必定位于三个两相平衡的连接线所组成的△DEF 的重心(是三相的质量重心,不是三角形的几何重心) 位置上,而且合金质量与三个相质量有以下关系: wN· Nd=wα· Dd wN· Ne=wβ· Ee wN· Nf=wγ· Ff 式中,wN、wα、wβ、wγ分别代表N合金及α、β、 γ相的质量,这就是三元系的重心法则,或称为重 心定律。
相 图 分 析
图5-7 三元匀晶相图
二、三元固溶体合金的结晶过程
三元匀晶转变与二元匀晶转变基本相同,两者都是 选择结晶,当液固两相平衡时,固相中高熔点组元的含 量较液相高;两者的结晶过程均需在一定温度范围内进 行,异类原子之间都要发生相互扩散。如果冷速较慢, 原子间的扩散能够充分进行,则可获得成分均匀的固溶 体;如果冷速较快,液固两相中原子扩散进行得不完全, 则和二元固溶体合金一样,获得存在枝晶偏析的组织。 欲使其成分均匀,需进行长时间的均匀化退火。但是两 者之间也有差别,在结晶过程中,在同一温度下,尽管 三元合金的液相和固相成分的连接线是条水平线,但液 相和固相成分的变化轨迹不位于同一个平面上。
第五章 三元合金相图
第一节 三元合金相图的表示方法 第二节 三元系平衡相的定量法则
第三节 三元匀晶相图
第四节 三元共晶相图
第五节 三元相图总结 第六节 三元合金相图应用举例
第一节 三元合金相图的表示方法
二元合金的成分中只有一个变量,其成分坐标轴 用一条直线表示,二元合金相图的主要部分是由一个 成分坐标轴和一个温度坐标轴所构成的平面中的一系 列曲线。三元相图与二元相图比较,组元数增加了一 个,成分变量是两个,故表示成分的坐标轴应为两个, 两个坐标轴构成一个平面,这样,再加上垂直于平面 的温度坐标轴,三元相图便成为一个三维空间的立体 图形。构成三元相图的主要部分应该是一系列空间曲 面,而不是二元相图中的那些平面曲线。
重 心 法 则
图5-6 三元系中的重心法则
第三节 三元匀晶相图
一、相 图 分 析
图5-7为三元匀晶相图的立体模型。图中ABC 是成 分三角形,三根垂线是温度轴,tA、tB、tC分别为三个 组元A、B、C 的熔点,三棱柱体的三个侧面是组元间形 成的二元匀晶相图,它们的液相线和固相线分别构成了 三元相图的两个空间曲面:上面那个向上凸的曲面叫做 液相面,下面那个向下凹的曲面叫做固相面。图中有三 个相区:液相面以上的空间为液相区,记为L;固相面以 下的空间为固相区,记为α;液相面和固相面之间的空 间为液固两相共存区,记为L+α。
