高考数学解答题常考公式及答题模板文理通用
【高考宝典】高考数学解答题常考公式及答题模板
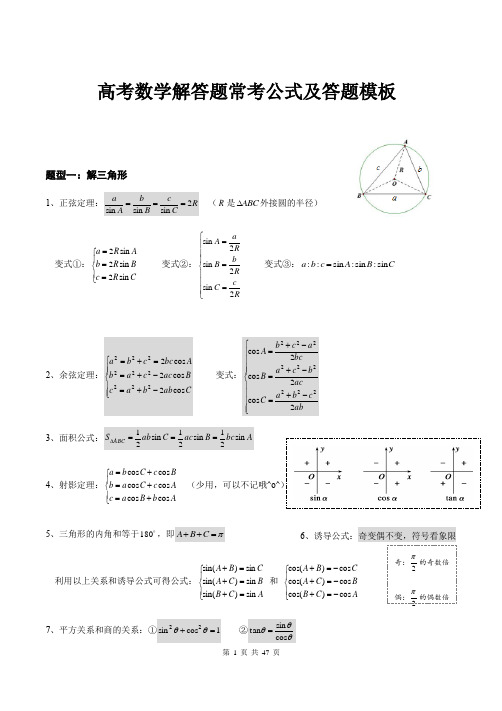
高考数学解答题常考公式及答题模板题型一:解三角形1、正弦定理:R CcB b A a 2sin sin sin === (R 是ABC ∆外接圆的半径) 变式①:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 变式②:⎪⎪⎪⎩⎪⎪⎪⎨⎧===Rc C R bB R a A 2sin 2sin 2sin 变式③:C B A c b a sin :sin :sin ::=2、余弦定理:⎪⎪⎩⎪⎪⎨⎧-+=-+==+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222 变式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 2222222223、面积公式:A bc B ac C ab S ABC sin 21sin 21sin 21===∆ 4、射影定理:⎪⎩⎪⎨⎧+=+=+=A b B a c A c C a b Bc C b a cos cos cos cos cos cos (少用,可以不记哦^o^)5、三角形的内角和等于 180,即π=++C B A6、诱导公式:奇变偶不变,符号看象限利用以上关系和诱导公式可得公式:⎪⎩⎪⎨⎧=+=+=+A C B B C A C B A sin )sin(sin )sin(sin )sin( 和⎪⎩⎪⎨⎧-=+-=+-=+A C B B C A CB A cos )cos(cos )cos(cos )cos(7、平方关系和商的关系:①1cos sin 22=+θθ ②θθθcos sin tan = 奇:2π的奇数倍 偶:2π的偶数倍8、二倍角公式:①θθθcos sin 22sin =②θθθθθ2222sin 211cos 2sin cos 2cos -=-=-= ⇒降幂公式:22cos 1cos 2θθ+=,22cos 1sin 2θθ-= ③θθθ2tan 1tan 22tan -=8、和、差角公式:①⎩⎨⎧-=-+=+βαβαβαβαβαβαsin cos cos sin )sin(sin cos cos sin )sin(②⎩⎨⎧+=--=+βαβαβαβαβαβαsin sin cos cos cos(sin sin cos cos cos())③⎪⎪⎩⎪⎪⎨⎧+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan( 9、基本不等式:①2ba ab +≤),(+∈R b a ②22⎪⎭⎫ ⎝⎛+≤b a ab ),(+∈R b a ③222b a ab +≤ ),(R b a ∈注意:基本不等式一般在求取值范围或最值问题中用到,比如求ABC ∆面积的最大值时。
高考数学答题模板12个(最新)

高考数学答题模板12个选择填空题1.易错点归纳九大模块易混淆难记忆考点分析,如概率和频率概念混淆、数列求和公式记忆错误等,强化基础知识点记忆,避开因为知识点失误造成的客观性解题错误。
针对审题、解题思路不严谨如集合题型未考虑空集情况、函数问题未考虑定义域等主观性因素造成的失误进行专项训练。
2.答题方法:选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法;填空题四大速解方法:直接法、特殊化法、数形结合法、等价转化法。
解答题专题一、三角变换与三角函数的性质问题1、解题路线图①不同角化同角②降幂扩角③化f(x)=Asin(ωx+φ)+h④结合性质求解。
2、构建答题模板①化简:三角函数式的化简,一般化成y=Asin(ωx+φ)+h的形式,即化为“一角、一次、一函数”的形式。
②整体代换:将ωx+φ看作一个整体,利用y=sin x,y=cos x的性质确定条件。
③求解:利用ωx+φ的范围求条件解得函数y=A sin(ωx+φ)+h的性质,写出结果。
④反思:反思回顾,查看关键点,易错点,对结果进行估算,检查规范性。
专题二、解三角形问题1、解题路线图(1) ①化简变形;②用余弦定理转化为边的关系;③变形证明。
(2) ①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。
2、构建答题模板①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的方向。
②定工具:即根据条件和所求,合理选择转化的工具,实施边角之间的互化。
③求结果。
④再反思:在实施边角互化的时候应注意转化的方向,一般有两种思路:一是全部转化为边之间的关系;二是全部转化为角之间的关系,然后进行恒等变形。
专题三、数列的通项、求和问题1、解题路线图①先求某一项,或者找到数列的关系式。
②求通项公式。
③求数列和通式。
2、构建答题模板①找递推:根据已知条件确定数列相邻两项之间的关系,即找数列的递推公式。
2024年高考数学知识点及公式整理汇总.doc

2024年高考数学知识点及公式整理汇总高中数学重点知识点全总结1、命题的四种形式及其相互关系是什么?(互为逆否关系的命题是等价命题。
)原命题与逆否命题同真、同假;逆命题与否命题同真同假。
2、对映射的概念了解吗?映射f:A→B,是否注意到A中元素的任意性和B 中与之对应元素的唯一性,哪几种对应能构成映射?(一对一,多对一,允许B中有元素无原象。
)3、函数的三要素是什么?如何比较两个函数是否相同?(定义域、对应法则、值域)4、反函数存在的条件是什么?(一一对应函数)求反函数的步骤掌握了吗?(①反解x;②互换x、y;③注明定义域)5、反函数的性质有哪些?①互为反函数的图象关于直线y=x对称;②保存了原来函数的单调性、奇函数性;6、函数f(x)具有奇偶性的必要(非充分)条件是什么?(f(x)定义域关于原点对称)1、抽样方法主要有:简单随机抽样(抽签法、随机数表法)常常用于总体个数较少时,它的特征是从总体中逐个抽取;系统抽样,常用于总体个数较多时,它的主要特征是均衡成若干部分,每部分只取一个;分层抽样,主要特征是分层按比例抽样,主要用于总体中有明显差异,它们的共同特征是每个个体被抽到的概率相等,体现了抽样的客观性和平等性。
2、对总体分布的估计——用样本的频率作为总体的概率,用样本的期望(平均值)和方差去估计总体的期望和方差。
3、向量——既有大小又有方向的量。
在此规定下向量可以在平面(或空间)平行移动而不改变。
4、并线向量(平行向量)——方向相同或相反的向量。
规定零向量与任意向量平行。
1、三类角的求法:①找出或作出有关的角。
②证明其符合定义,并指出所求作的角。
③计算大小(解直角三角形,或用余弦定理)。
2、正棱柱——底面为正多边形的直棱柱正棱锥——底面是正多边形,顶点在底面的射影是底面的中心。
正棱锥的计算集中在四个直角三角形中:3、怎样判断直线l与圆C的位置关系?圆心到直线的距离与圆的半径比较。
直线与圆相交时,注意利用圆的“垂径定理”。
2024年高考数学知识点与公式整理.doc

2024年高考数学知识点与公式整理高三数学公式知识点三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a=tana·tan(π/3+a)·tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2 cos^2(α)=(1+cos(2α))/2=covers(2α)/2 tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina_2sin[(60+a)/2]cos[(60°-a)/2]_2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa_2cos[(a+30°)/2]cos[(a-30°)/2]_{-2sin[(a+30°)/2]sin[(a-30°) /2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cos β·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cos β·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tan β-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ=2sin[(θ+φ)/2]cos[(θ-φ)/2]sinθ-sinφ=2cos[(θ+φ)/2]sin[(θ-φ)/2]cosθ+cosφ=2cos[(θ+φ)/2]cos[(θ-φ)/2]cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ=[cos(α-β)-cos(α+β)]/2cosαcosβ=[cos(α+β)+cos(α-β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2cosαsinβ=[sin(α+β)-sin(α-β)]/2诱导公式sin(-α)=-sinαcos(-α)=cosαtan(—a)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαcos(π+α)=-cosαtanA=sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限高中数学知识点一、圆及圆的相关量的定义1.平面上到定点的距离等于定长的所有点组成的图形叫做圆。
高考数学解答题常考公式及答题模板(文理)(wenli )

高考数学解答题常考公式及答题模板题型一:解三角形1、正弦定理:R CcB b A a 2sin sin sin === (R 是ABC ∆外接圆的半径) 变式①:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 变式②:⎪⎪⎪⎩⎪⎪⎪⎨⎧===Rc C R bB R a A 2sin 2sin 2sin 变式③:C B A c b a sin :sin :sin ::= 2、余弦定理:⎪⎪⎩⎪⎪⎨⎧-+=-+==+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222 变式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 2222222223、面积公式:A bc B ac C ab S ABC sin 21sin 21sin 21===∆ 4、三角形的内角和等于ο180,即π=++C B A 5、诱导公式:奇变偶不变,符号看象限利用以上关系和诱导公式可得公式:⎪⎩⎪⎨⎧=+=+=+A C B B C A CB A sin )sin(sin )sin(sin )sin(和⎪⎩⎪⎨⎧-=+-=+-=+A C B B C A CB A cos )cos(cos )cos(cos )cos(6、平方关系和商的关系:①1cos sin 22=+θθ ②θθθcos sin tan =7、二倍角公式:①θθθcos sin 22sin =②θθθθθ2222sin 211cos 2sin cos 2cos -=-=-= ⇒降幂公式:22cos 1cos 2θθ+=,22cos 1sin 2θθ-= ③θθθ2tan 1tan 22tan -=8、和、差角公式:①⎩⎨⎧-=-+=+βαβαβαβαβαβαsin cos cos sin )sin(sin cos cos sin )sin( ②⎩⎨⎧+=--=+βαβαβαβαβαβαsin sin cos cos cos(sin sin cos cos cos())③⎪⎪⎩⎪⎪⎨⎧+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan( ba ++2⎫⎛+b a +22b a +奇:2π的奇数倍 偶:2π的偶数倍注意:基本不等式一般在求取值范围或最值问题中用到,比如求ABC ∆面积的最大值时。
关于高考数学答题模板及技巧有哪些.doc

关于高考数学答题模板及技巧有哪些高中数学答题模板整理1、高考数学选择填空题答题方法高考数学选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法。
填空题四大速解方法:直接法、特殊化法、数形结合法、等价转化法。
2、高中数学解答题答题技巧与模板1)三角变换与三角函数的性质问题一、解题路线图①不同角化同角②降幂扩角③化f(x)=Asin(ωx+φ)+h④结合性质求解。
二、构建答题模板①化简:三角函数式的化简,一般化成y=Asin(ωx+φ)+h的形式,即化为“一角、一次、一函数”的形式。
②整体代换:将ωx+φ看作一个整体,利用y=sinx,y=cosx的性质确定条件。
③求解:利用ωx+φ的范围求条件解得函数y=Asin(ωx+φ)+h的性质,写出结果。
④反思:反思回顾,查看关键点,易错点,对结果进行估算,检查规范性。
2)高中数学解三角形问题一、解题路线图①化简变形;②用余弦定理转化为边的关系;③变形证明。
①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。
二、构建答题模板①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的方向。
②定工具:即根据条件和所求,合理选择转化的工具,实施边角之间的互化。
③求结果。
④再反思:在实施边角互化的时候应注意转化的方向,一般有两种思路:一是全部转化为边之间的关系;二是全部转化为角之间的关系,然后进行恒等变形。
3)数列的通项、求和问题一、数学解题路线图①先求某一项,或者找到数列的关系式。
②求通项公式。
③求数列和通式。
二、构建答题模板①找递推:根据已知条件确定数列相邻两项之间的关系,即找数列的递推公式。
②求通项:根据数列递推公式转化为等差或等比数列求通项公式,或利用累加法或累乘法求通项公式。
③定方法:根据数列表达式的结构特征确定求和方法(如公式法、裂项相消法、错位相减法、分组法等)。
④写步骤:规范写出求和步骤。
高考数学解答题常考公式及答题模板 精编版

例16:某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人。第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
第一种生产方式
由 ,得
.……先写出通项公式的一般式,再带值
又 成等比数列……利用等比中项列出方程
.
(2)由(1)知:
……运用分组求和法
记 , ,则
.
6、基本不等式:
① ② ③
注意:基本不等式一般在求取值范围或最值问题的时候用到,有时还用于证明数列不等式。
☞答题步骤:
①抄条件:先抄题目所给的条件;(但不要抄题目)
②写公式:写出要用的公式,如等差数列的通项公式或前n项和;
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ,且四棱锥P−ABCD的体积为 ,求该四棱锥的侧面积.
证明:(1) ……写出题目的已知条件
①
又 ②……将证明的条件圈出来
……说明清楚线与面的关系
又 .……根据线面垂直的性质,得出结论
(2)过P点作 ,垂足为点M,如图所示:……作辅助线一定要有说明
累加后,得
……利用了公式
故 .
(5)累乘法:形如 ,且 可用求积,可用累乘法
例6:已知数列 中, , ,求 .
解:已知
累乘后,得
.
(6)取倒数法:形如 (p,q为非零常数)则两边同时取倒数
例7:已知数列 满足 且 ,求 .
解:已知 ……等式两边同时取倒数
……满足等差数列的定义
令 ,则 ……构造等差数列
2020年高考数学答题步骤模板

6、诱导公式:奇变偶不变,符号看象限
sin( A B) sin C
cos( A B) cos C
利用以上关系和诱导公式可得公式: sin( A C) sin B 和 cos( A C) cos B
sin(B C) sin A
cos(B C) cos A
奇: 的奇数倍 2
高考数学解答题常考公式及答题模板
(文理通用)
题型一:解三角形
1、正弦定理: a b c 2R ( R 是 ABC 外接圆的半径) sin A sin B sin C
a 2R sin A 变式①: b 2R sin B
c 2R sin C
sin
A
a 2R
变式②:
sin
B
b 2R
sin C
Sn
a1 2, a2 a4 8
an a1 (n 1)d
a2 a4 (a1 d ) (a1 3d ) 2a1 4d 8
a1 2d 4 d 1
an a1 (n 1)d n 1
a3 am
a1 3d 4 a1 (m 1)d
m
1
a1, a3 , am
9、基本不等式:① ab a b (a,b R ) 2
② ab a b 2 (a,b R ) 2
③ ab a2 b2 (a, b R) 2
注意:基本不等式一般在求取值范围或最值问题中用到,比如求 ABC 面积的最大值时。
说明:颜色加深的是重点记忆的公式哦!
第 1 页 共 33 页
②若已知
an 1 an
q 和 a1
a ,则用等比数列通项公式 an
a1q n1
(2) an 与 Sn 的关系: an
S1 Sn
