椭圆与超椭圆曲线公钥密码的理论与实现(王学理,裴定一著)思维导图
椭圆曲线密码学知识简介

(3)
设(x1,y1) ∈E(Fp),y1≠0,则2(x1,y1)=(x3,y3),其中
x3= α2-2x1, y3=α(x1-x3)-y1
这里α=(3x12+a)/(2y1)
(4)
注:若#E(Fp)=p+1,曲线E(Fp)称为超奇异的,否则称为
其中a1,b1不同时为0;a2,b2也不同时为0。 设
D= a1 b1
Dx= b1 c1 Dy= c1 a1
a2 b2
b2 c2
c2 a2
若D≠0,则两直线L1,L2相交于一平常点P(x,y),其坐标为 x=Dx/D,y=Dy/D.
这组解可表为:x/Dx=y/Dy=1/D
(约定:分母Dx,Dy有为0时,对应的分子也要为0)
令Fq表示q个元素的有限域,用E(Fq)表示定义在Fq上 的一个椭圆曲线E。
定理1.(Hass定理) E(Fq)的点数用#E(Fq)表示,则
| #E(Fq)-q-1|≤2q1/2
(1) Fp(素域,p为素数)上椭圆曲线 令p>3,a,b∈Fp,满足4a3+27b2≠0,由参数a和b定
义的Fp上的一个椭圆曲线方程为:
椭圆曲线E是一个光滑的Weierstrass方程在P2(K)中的 全部解集合。
Y2Z+a1XYZ+a3YZ2=X3+a2X2Z+a4XZ2+a6Z3 注:
a) 在椭圆曲线E上恰有一个点,称之为无穷远点。即(0:1:0) 用θ表示。
b) 可用非齐次坐标的形式来表示椭圆曲线的Weierstrass 方程:
AP → L2
可设想L1上有一点P∞,它为L2和L1的交点,称之为无穷远 点。
现现代密学 第10讲ECC

2019/11/11
6
ECC上的密码
应用
Diffie-Hellman密钥交换
Elgamal密码体制
安全基础
ECC 本身还有许多需要研究提高的地方如高速ECC 密码算法芯片的研
制等.
2019/11/11
16
ECC未来主要研究
快速算法的研究 ECC的离散对数问题 ECC上编码方法的研究 超椭圆曲线
2019/11/11
17
对ECC的 攻击
至今没有发现比较有效的计算ECDLP 的方法, 目前计算ECDLP 的最好算法仍然是指数时间的 并行Pollard-rho 方法.
ECC上的离散对数问题是困难问题
在ECC构成的交换群Ep(a,b)上考虑方程 Q=kP,P,Q∈Ep(a,b),k<p.由k和P求Q 容易,由P,Q求k则是困难的。
2019/11/11
7
Diffie-Hellman密钥交换
取Ep(a,b),生成元G(x1,y1) (p≈2180, |G|大素数) Ep(a,b)和G公开
GF(P)上ECC点的个数?个数越多,越安全. Hasse定理
如果E是定义在GF(p)域上的椭圆曲线,N是E 上的点的个数,则:
N(p1)2 p
椭圆曲线加法的定义
Q+R: Q、 R连线与E交点关于x轴对称点
Q+R=-P
O为加法单位元 P+O=P
P (x,y)加法逆元-P(x,-y) P+(-P)否=则O导致加
椭圆曲线密码(PDF)

内容安全研究室朱潜报告的主要内容⏹群和域的相关概念⏹椭圆曲线的定义和运算法则⏹椭圆曲线离散对数问题⏹椭圆曲线密码体制⏹椭圆曲线密码的优势⏹曲线密码体制的应用为什么要在有限域上研究椭圆曲线密码?密码学常在有限域的基础上研究椭圆密码曲线,在有限域的椭圆m基础上。
基于有限域Fp,而不是使用实数域、曲线主要是基于Fp和F2是因为实数计算时会产生截段误差,无法满足密码算法的精确性,而m是由于可以在计算机处理时大大提且实数运算的速度很慢。
基于F2高处理速度。
群和域的相关概念定义1:任意给定一个非空集合F和其上的二元运算“*”,如果满足(1)封闭性:对任意a,b∈F,存在c ∈F,使得c=a*b ∈F;(2)结合律:对于任意a,b∈F,都有(a*b)*c=a*b*c;(3)单位元e存在:即存在e ∈F,对于任意a ∈F,都有a*e=e*a;(4)逆元存在:对于任意a ∈F,存在b ∈F,使得a*b=b*a=e;则称集合F关于二元运算“*”构成群,记为(F,*)。
在群(F,*)中,如果对于任意a ,b∈F,都有a*b=b*a,则称群(F,*)是交换群,也称为阿贝尔(Abel)群。
定义2:设“+”,“*”是G上的二元运算,如果满足:(1)(G,+)是一个交换群,其单位元记为0;(2)(G-{0},*)是交换群,其单位元记为1;(3)运算“*”对“+”可分配,即对任意a ,b,c∈G,都有a*(b+c)=a*b+a*c(a+b)*c=a*c+b*c则称(G,+,*)是域。
群和域的相关概念定义3:有限域,如果域F中的元素个数有限,则称F为有限域或伽罗华域,其中F中的元素个数称为有限域F的阶,记为∣F ∣。
对有限域而言,其元素的个数必为一素数的方幂。
即存在一个q阶有限域F,当且仅当q是一个素数的幂,即q=p m,其中,p是一个素数,并称为域F的特征,m是一个正整数。
若m=1,则域F就称为素域。
定义4:设p是一个素数,以p为模,则模p的全体余数的集合{0,1,2,……,p-1}关于模p的加法和乘法构成一个p阶有限域,简称素域,并且用符号Fp表示。
椭圆曲线密码ppt课件

⑴ 密钥生成
• 用户随机地选择一个整数d作为自己的秘密的解 密钥,2≤d≤p-2 。
• 计算y=αd mod p,取y为自己的公开的加密钥。 • 由公开钥y 计算秘密钥d,必须求解离散对数,
由于上述运算是定义在模p有限域上的,所以称为 离散对数运算。
③从x计算y是容易的。可是从y计算x就困难得多, 利用目前最好的算法,对于小心选择的p将至少 需用O(p ½)次以上的运算,只要p足够大,求解 离散对数问题是相当困难的。
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
要小,所以ELGamal密码的加解密速度比RSA稍快。 ②随机数源
由ELGamal密码的解密钥d和随机数k都应是高质量 的随机数。因此,应用ELGamal密码需要一个好的随机 数源,也就是说能够快速地产生高质量的随机数。 ③大素数的选择
为了ELGamal密码的安全,p应为150位(十进制数) 以上的大素数,而且p-1应有大素因子。
三、椭圆曲线密码
2、椭圆曲线
②定义逆元素
设P(x1 ,y1)和Q(x2 ,y2)是解点,如果 x1=x2 且y1=-y2 ,则
P(x1 ,y1)+Q(x2 ,y2)=0 。
这说明任何解点R(x ,y)的逆就是
R(x ,-y)。
注意:规定无穷远点的逆就是其自己。
O(∞,∞)=-O(∞,∞)
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的,因 此,篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
三、椭圆曲线密码
最新椭圆曲线公钥密码体制(ECC)ppt课件

群
群(G, *)是由集合G和集合上的二元运算* 组成的代数系统,群应满足如 下的性质 :
1、封闭性 : 对于任意的 x,y ∈G,满足 x * y G 2、结合律 :对于任意的 x,y, z ∈G, 满足:
(x * y) * z = x * (y * z) 3、有单位元素 : 存在单位元素 e ∈ G ,满足:
例题
仍以E23(1,1)为例,设P=(3,10),Q=(9,7),求P+Q
710 3 111mod23
93 6 2 x3 112 3910917mod23 y3 11(317)1016420mod23
所以P+Q=(17,20),仍为E23(1,1)中的点。
求点P的2倍
若 P = (xP , yP) 若 yP 不为 0 2P = R 按如下方法计算:
g5 = (111) g6 = (101) g7 = (001) = 1 1.方程 y2 + xy = x3 + g5x2 + g6是否定义了F(23)上的 一个椭圆曲
线? 2. 问点 P(g3, g6)和 Q(g5, g2) 是否位于F(23)上的椭圆曲线 y2 + xy
= x3 + g2 x2 + g6 之上? 3. 求F(23)上的如下椭圆曲线的点的加法逆元?
椭圆曲线E23(1,0) 的点的构造
满足条件的23个点是: (0,0) (1,5) (1,18) (11,10) (11,13) (13,5) (15,20) (16,8) (16,15) (18,10) (18,13) (19,1) (20,19) (21,6) (21,17)
(9,5) (13,18) (17,10) (19,22)
椭圆曲线加密算法(一)

椭圆曲线加密算法(⼀)椭圆曲线加密和签名算法简述椭圆曲线密码学,简称ECC。
是⼀种建⽴公开加密的算法,也就是⾮对称加密。
和RSA类似。
被公认在给定密钥长度下最安全的加密算法。
应⽤范围很⼴,主要的三个技术TLS、PGP、SSH都在使⽤它,特别是以BTC为代表的数字货币。
椭圆曲线椭圆曲线并不是我们⾼中时学习的椭圆形状,其名字的由来是应为椭圆曲线的描述⽅程,类似于计算⼀个椭圆周长的⽅程。
这⾥⽤来加密的椭圆曲线的定义是⼀个特殊情况。
椭圆曲线暂时可以简单的理解为:其中:a和b决定了曲线在坐标系的不同形状。
举个例⼦:当b=1,a的取值从2到-3时,曲线的形状如下:特殊曲线:当a=b=0时(左),或a=-3,b=2时(右),这两条都不是符合标准的曲线。
阿贝尔群数学上,群是指定义了⼆元操作运算并且⽤符号“+”表⽰的⼀个集合。
则必须满⾜以下要求:封闭性:如果a和b都是群成员,那么a+b也是群成员。
组合性:(a+b)+c=a+(b+c)单位元:存在确切的⼀个值可以保证 a+0=0+a=a成⽴,我们称之为单位元逆元:每个成员都有⼀个相反数:对于任意值a必定存在b使得a+b=0这样的群我们称之为阿贝尔群。
另外阿贝尔群还应该满⾜交换律a+b=b+a我们所熟知的在整数范围内的加法运算(Z,+)就是阿贝尔群封闭性:a、b属于整数,a+b也属于整数组合性:(a+b)+c=a+(b+c)单位元:0值就是单位元逆元:a的逆元就是-a所以(Z,+)是⼀个阿贝尔群。
椭圆曲线的加法假设我们有这样⼀条椭圆曲线y2=x3-x,曲线上有两点P、Q,过P和Q做⼀条直线,交椭圆曲线于R'点,再过R'点做垂直于X轴的直线,交椭圆曲线于另⼀点R,我们定义P+Q=R。
当P=Q时候,则是过P点的切线交于椭圆曲线于R',此时R=2P,如图所⽰:当有k个相同的点P相加时,记做kP,如:P+P+P=2P+P=3P,如图:椭圆曲线密码利⽤上述“运算”中的“椭圆曲线上的离散多数问题”,就像RSA利⽤“⼤数质因数分解”⼀样。
区块链中的密码学(三)-椭圆曲线加密算法分析
区块链中的密码学(三)-椭圆曲线加密算法分析在⽬前密码学的⾮对称加密算法中,RSA算法依然是⼀种主流,但是随着⽐特币中对于⼀种之前不太流⾏的算法:椭圆加密算法(ECC)的成功应⽤后,这种算法得到了很⼤的关注和普及。
有⼀种说法是中本聪不信任RSA算法,认为美国⼈在其中留有后门,⽽据斯诺登的爆料也确实如此。
相较RSA,ECC不仅在某种程度上杜绝所谓留有后门的情况,⽽且加密性能/安全性都有提⾼。
本⽂就带⼤家⼀窥ECC算法的天地。
鉴于ECC算法对数学知识要求⽐较⾼,不像RSA依赖于中学数学的⽔平,ECC⽤到了许多《近世代数基础》,《初等数论》的知识,本⽂将从⼀个密码学爱好者并区块链的⾓度,讲述⼀下ECC在区块链中的应⽤。
什么是椭圆曲线加密(ECC)?椭圆曲线可以简单的理解为公式:这是⼀个数学公式,它的理论基础要从平⾏线谈起。
数学上⼈们认为的平⾏线永不相交,这在某种程度上是⽆法验证的,因为没有⼀个⽆限远处的概念,假设平⾏线在⽆限远处相交,这样的好处是所有的直接都有且只有⼀个焦点,那么基于这个事实,我们中学学过的笛卡尔平⾯直⾓坐标系可以映射出另外⼀个平⾯坐标系:假设平⾯直⾓坐标系中有点A(x,y),我们定义 X= x/z,Y = y/z,Z=z;那么联⽴⽅程:aX+bY+c1Z =0; aX+bY+c2Z =0 可以计算出z=0;所以我们新的坐标系中的点可以表⽰为:(X:Y:0);这是椭圆曲线建⽴的坐标系基础。
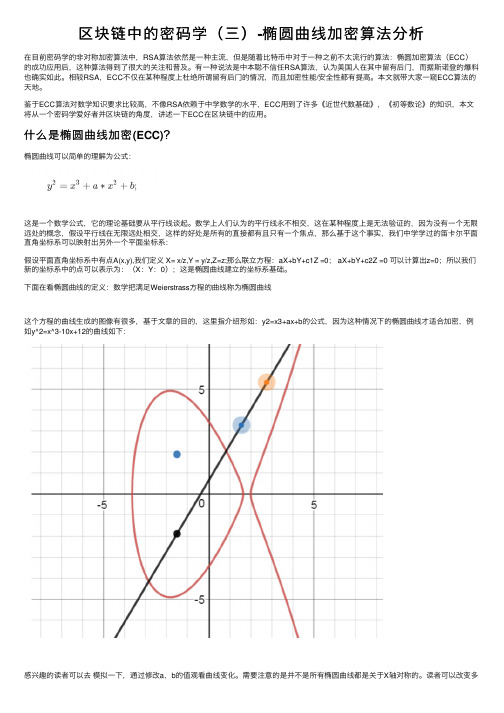
下⾯在看椭圆曲线的定义:数学把满⾜Weierstrass⽅程的曲线称为椭圆曲线这个⽅程的曲线⽣成的图像有很多,基于⽂章的⽬的,这⾥指介绍形如:y2=x3+ax+b的公式,因为这种情况下的椭圆曲线才适合加密,例如y^2=x^3-10x+12的曲线如下:感兴趣的读者可以去模拟⼀下,通过修改a,b的值观看曲线变化。
需要注意的是并不是所有椭圆曲线都是关于X轴对称的。
读者可以改变多改变a1的值来发现。
数学家在这个曲线上定义了⼀种椭圆曲线的加法,在上⾯定义的公式曲线图中:显然这并不是传统的数学上的加法,运算法则:任意取椭圆曲线上两点P、Q (若P、Q两点重合,则做P点的切线)做直线交于椭圆曲线的另⼀点R,过R做y轴的平⾏线交于R’。
现代密码学_第10讲ECC

Elliptic Curve Cryptography
2011-1-16
1
椭圆曲线
椭圆曲线的曲线方程是以下形式的三次方程 y2+axy+by=x3+cx2+dx+e a,b,c,d,e是满足某些简单条件的实数 是满足某些简单条件的实数。 a,b,c,d,e是满足某些简单条件的实数。定义中包含一个 称为无穷远点的元素, 称为无穷远点的元素,记为O.
Hasse定理 定理
如果E是定义在 域上的椭圆曲线, 是 如果 是定义在GF(p)域上的椭圆曲线,N是E 是定义在 域上的椭圆曲线 上的点的个数, 上的点的个数,则:
N − ( p + 1) ≤ 2 p
椭圆曲线加法的定义
Q+R: Q、 R连线与 交点关于 轴对称点 连线与E交点关于 、 连线与 交点关于x轴对称点 Q+R=-P O为加法单位元 P+O=P 为加法单位元 P (x,y)加法逆元 加法逆元-P(x,-y) P+(-P)=O 加法逆元 否则导致加 法运算无意 当4a3+27b2≠0 mod p Ep(a,b)构成加法交换群 构成加法交换群 2011-1-16
2011-1-16
3
28个点 个点
点集如何产生方法? 点集如何产生方法
对每一x(0≤x<p且x为整数),计算x3+ax+b mod p 0≤x<p且 为整数),计算x 0≤x<p ),计算 决定求出的值在模p下是否有平方根 下是否有平方根, 决定求出的值在模 下是否有平方根,如果没有则椭 圆曲线上没有与这一x对应的点 如果有, 对应的点; 圆曲线上没有与这一 对应的点;如果有,则求出两 个平方根。 个平方根。 对应每个x,都有 个点. 除(4,0),对应每个 都有 个点 对应每个 都有2个点 GF(P)上ECC点的个数?个数越多 越安全 个数越多,越安全 上 点的个数 个数越多 越安全.
