拉普拉斯变换 数学物理方程
数学物理方法 拉氏变换

1 c j st (1)利用公式 f (t ) F (s)e ds c j 2 πj
(2)对简单形式的F(s)可以查拉氏变换表得原函数 (3)把F(s)分解为简单项的组合
F ( s ) F1 ( s ) F2 ( s ) Fn ( s )
f (t ) f1 (t ) f 2 (t ) f n (t )
K2 Kn ( s p1 ) F (s) K1 ( s p1 ) s p s p 2 n
令 s = p1 方法2
求极限的方法
N (s)(s pi ) K i lim s pi D(s)
返 回 上 页 下 页
N (s)(s pi ) K i lim s pi D(s)
2. 拉氏变换的定义
定义 [ 0 , ∞)区间函数 f(t)的拉普拉斯变换式:
简写 F (s) L f (t ) , f (t ) L F (s)
-1
F ( s ) f (t )e st dt 0 1 c j st F ( s ) e d s f (t ) c j 2 πj
s 1
3
d K 21 [( s 1) 2 F ( s )] s 1 d [ s 4 ] 4 s 1 ds ds s
f (t ) 4 4e 3te
t
t
返 回
上 页
下 页
小结 由F(s)求f(t) 的步骤: n =m 时将F(s)化成真分式和多项式之和 N 0 (s) F (s) A D(s)
(2) f (t ) δ ( t )的象函数
1 L[ (t )] s d (t ) 1 L (t ) L[ ] s 0 1 dt s 2 d f ( t ) ' 推广:L[ ] s[ sF ( s) f (0 )] f (0 ) 2 dt 2 ' s F ( s) sf (0 ) f (0 )
数学物理方程第六章-拉普拉斯变换
L [
1
p 2 p 9 p 36
3 2
p 81
4
2
]
p 81
4
p 2 p 9 p 36 ( p 3 )( p 3 )( p 9 )
2
1 2
1 p3
1 2
1 p3
p p 9
2
1 3
3 p 9
2
L [
1
p 2 p 9 p 36
0
( ) d 0
L [ f ( at )] 1 a f(
0
#
p a ).
(4) 相似定理 (5) 位移定理 (6) 延迟定理
L[e
t
f ( t )] f ( p ).
与傅立叶变换类似
(t t 0 ) H (t t 0 )
(t )
L [ f ( t t 0 )] e
pt
dt ,
0
L [ tf ( t )]
.
L [ t f ( t )] ( 1)
n
n
d L [ f ( t )] dp
n
n
.
2012-8-1
阜师院数科院
2. 性质 与傅立叶变换同为积分变换,故有类似性质 (1) 线性定理 若
L [ f 1 ( t )] f 1 ( p )
和
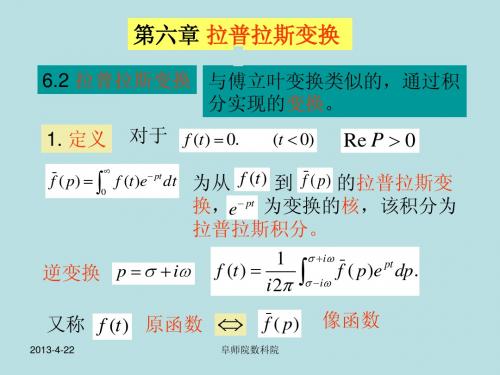
第六章 拉普拉斯变换
6.2 拉普拉斯变换 与傅立叶变换类似的,通过积 分实现的变换。 1. 定义
f ( p)
对于
f (t )e
pt
f (t ) 0 .
(t 0 )
数学物理方法1课件——第六章 拉普拉斯变换

解:按照拉普拉斯变换的定义,有
∫ ∫ ∞ sin ωt e− ptdt = 1
0
2i
∞ 0
⎡⎣e−(
p −iω
)t
− e−( p+iω)t ⎤⎦ dt =
1⎡ 1
2i ⎢⎣ p − iω
−
p
1
+ iω
⎤ ⎥⎦
=
ω p2 +ω2
sin ωt
U
ω p2 +ω2
类似地,有
∫ ∫ ∞ cosωt e− ptdt = 1
f (n) (t) U pn F ( p) − pn−1 f (0) − pn−2 f (1) (0) − ... − f (n−1) (0)
通过拉普拉斯变换,把原函数的微商运算转化为像函数的乘法 运算,而且还自动包括了原函数的初值。
例2 已知函数f(t)满足如下二阶常微分方程
d 2 f (t) + ω2 f (t) = 0
∞
∑ f (x) = cneiknx n=−∞
∫ 其中kn=nπ/l 为波数
cn
=
1 2l
l f (x)e−iknxdx
−l
¾ 实数形式的傅里叶积分变换
∞
∞
f (x) = ∫0 A(k) cos(kx)dk +∫0 B(k) sin(kx)dk
其中
∫ A(k) = 1
∞
f (x) cos(kx)dx
=
−
1
0
p
∞ tde− pt
0
=
−
1 p
⎡⎢⎣te− pt
∞ 0
−
∞ 0
e−
pt
dt
⎤ ⎥⎦
数学物理方法 第六章 拉普拉斯变换

ω
p2 + ω2
1 (3)由于 2 ⇔ sin ωt , ⇔ e −( R L ) t p + ω2 p+R L 引用卷积定理完成反演, E0 t −( R L )( t −τ ) E0 −( R L ) t ( R L )τ ( R L) sin ωt − ω cos ωt t j (t ) = sin ωτdτ = {e [e ] |0 } 2 2 2 ∫0 e L L R L +ω E0 ( R L) sin ωt − ω cos ωt E0 ωe −( R L ) t = + 2 2 2 L R L +ω L R 2 L2 + ω 2
wuxia@
至于它在初始时刻之前的值,不关心,不妨 设f(t)=0 (t<0)。 为了获得宽松的变换条件,把f(t)加工为 g(t)=e-σt f(t). e-σt 是收敛因子,即,正实数σ 的值选的足够大,以保证g(t)在(-∞,∞)上绝 对可积。 于是,可以对g(t)做傅里叶变换,
− 3 2
wuxia@
−
(二)查表法
e −τp 例2:求 解: 1 1 查表得 , ⇔ πt p e −τp 1 再利用延迟定理 ⇔ p π (τ − t ) p 的原函数.
wuxia@
ω p+λ 例3:求 和 的原函数。 2 2 2 2 ( p + λ) + ω ( p + λ) + ω
t0 ∞ − p ( ξ + t0 )
dξ = e
− pt0
∫
∞
t0
f (ξ )e
− pξ
dξ = e
− pt0
−
f ( p)
第五章 拉普拉斯变换-数学物理方法

d2 L[t 2 f ( t )] ( 1)2 2 F ( p) dp
……
dn n pt n F ( p) ( t ) f ( t )e dt ( 1) [t n f ( t )]e pt dt n 0 0 dp
dn L[t n f ( t )] ( 1)n n F ( p) dp
这个性质很容易从Laplace变换的定义得到,因为它只不 过是积分运算的线性性质的反映.
77
性质2 :原函数的导数的拉氏变换
L 设f (t)及 f ' (t ) 都满足拉氏变换存在的充分条件, [ f ( t )] F ( p),
则: 0 f ( t )e dt f ( t ) e
' pt
n n
【证明
】 F ( p) f ( t )e pt dt
0
d pt F ( p) t f ( t )e dt [t f ( t )]e pt dt 0 0 dp d L[t f ( t )] F ( p) dp 2 d 2 pt 2 F ( p) ( t ) f ( t )e dt ( 1) [t 2 f ( t )]e pt dt 2 0 0 dp
L[ f ( t )] f ( t )e
'' '' 0 pt
dt e
0
pt
df ( t ) f ( t ) e
' '
pt 0
p f ' ( t )e pt dt
0
f ' (0) p[ pF ( p) f (0)] p2 F ( p) pf (0) f ' (0)
拉普拉斯方程

➢ 实微分定理
L
df (t) dt
sF (s)
f
(0),
f (0) f (t) t 0
证明:
由于
f (t)est dt 0
e st f (t)
s
0
df (t ) est 0 dt s
dt
版权所有,盗版必究!
第 5 页 共 18 页
满哥制作
复变函数—拉普拉斯(Laplace)方程
B'(s)
B'( pi )
例 1:求
F (s)
s2 s 2 s(s 2 s 6) 的原函数
f(t)。
解:
F(s)
s2 s 2 s(s2 s 6)
s2 s 2 s(s 3)(s 2)
A1 s
A2 s3
A3 s2
A1
sF (s) s0
s2 s 2
(s
3)(s
2)
正弦及余弦函数
sin t 1 e j t e j t 2j
版权所有,盗版必究!cos t
第
12 页
共
e
j18 页t
e j t
满哥制作
2
复变函数—拉普拉斯(Laplace)方程
由欧拉公式,有:
从而: L[sint ] 1 e jt e st dt e jt e st dt
2j 0
0
同理:
1 2j
s
1
j
L[coss2
t ]
2
s
1
sj
sR2 e(s) 02
单位脉冲函数 (t)
f(t)
1
0
t
单位脉冲函数
0
(t
)
laplace变换公式表
ω/(s^2 + ω^2) • 阶跃函数与余弦函数的乘积:f(t) = cos(ωt)u(t),F(s) =
s/(s^2 + ω^2) 2. 公式的线性性质:如果 f(t) 和 g(t) 的拉普拉斯变换分别是 F(s) 和 G(s),那么 a·f(t) + b·g(t) 的拉普拉斯变换是 a·F(s) + b·G(s),其 中 a 和 b 是常数。 3. 积分定理:如果 F(s) 是 f(t) 的拉普拉斯变换,那么 ∫[0, t] f(τ) dτ 的拉普拉斯变换是 F(s)/s。
以下是常见的拉普拉斯变换公式表:
1. 时间域函数:f(t) 的拉普拉斯变换 F(s): • 常数函数:f(t) = A,F(s) = A/s • 单位阶跃函数:f(t) = u(t),F(s) = 1/s • 单位冲激函数(Dirac Delta 函数):f(t) = δ(t),F(s) = 1 • 指数衰减函数:f(t) = e^(-at),F(s) = 1/(s + a) • 正弦函数:f(t) = sin(ωt),F(s) = ω/(s^2 + ω^2) • 余弦函数:f(t) = cos(ωt),F(s) = s/(s^2 + ω^2) • 阶跃函数与指数衰减的乘积:f(t) = e^(-at)u(t),F(s) = 1/(s
这些是常体的函数形式和条件使用相应的公式。注意,拉普拉斯变换 的具体定义和性质可能因不同的文献和应用而有所不同,因此在具体问题中请 参考相应的参考资料和教材。
Laplace拉氏变换公式表
Laplace拉氏变换公式表1. 常数变换:对于常数C,其拉普拉斯变换为C/s,其中s是复数频率。
2. 幂函数变换:对于幂函数t^n,其中n为实数,其拉普拉斯变换为n!/s^(n+1)。
3. 指数函数变换:对于指数函数e^(at),其中a为实数,其拉普拉斯变换为1/(sa)。
4. 正弦函数变换:对于正弦函数sin(at),其中a为实数,其拉普拉斯变换为a/(s^2+a^2)。
5. 余弦函数变换:对于余弦函数cos(at),其中a为实数,其拉普拉斯变换为s/(s^2+a^2)。
6. 双曲正弦函数变换:对于双曲正弦函数sinh(at),其中a为实数,其拉普拉斯变换为a/(s^2a^2)。
7. 双曲余弦函数变换:对于双曲余弦函数cosh(at),其中a为实数,其拉普拉斯变换为s/(s^2a^2)。
8. 指数衰减正弦函数变换:对于指数衰减正弦函数e^(at)sin(bt),其中a和b为实数,其拉普拉斯变换为b/(s+a)^2+b^2。
9. 指数衰减余弦函数变换:对于指数衰减余弦函数e^(at)cos(bt),其中a和b为实数,其拉普拉斯变换为s+a)/(s+a)^2+b^2。
10. 指数增长正弦函数变换:对于指数增长正弦函数e^(at)sin(bt),其中a和b为实数,其拉普拉斯变换为b/(sa)^2+b^2。
Laplace拉氏变换公式表11. 幂函数与指数函数的乘积变换:对于函数t^n e^(at),其中n为实数,a为实数,其拉普拉斯变换为n!/(sa)^(n+1)。
12. 幂函数与正弦函数的乘积变换:对于函数t^n sin(at),其中n为实数,a为实数,其拉普拉斯变换可以通过分部积分法得到。
13. 幂函数与余弦函数的乘积变换:对于函数t^n cos(at),其中n为实数,a为实数,其拉普拉斯变换可以通过分部积分法得到。
14. 指数函数与正弦函数的乘积变换:对于函数e^(at) sin(bt),其中a和b为实数,其拉普拉斯变换为b/(sa)^2+b^2。
拉普拉斯方程
拉普拉斯方程拉普拉斯方程(Laplace equation)拉普拉斯方程表示液面曲率与液体压力之间的关系的公式。
一个弯曲的表面称为曲面,通常用相应的两个曲率半径来描述曲面,即在曲面上某点作垂直于表面的直线,再通过此线作一平面,此平面与曲面的截线为曲线,在该点与曲线相重合的圆半径称为该曲线的曲率半径R1。
通过表面垂线并垂直于第一个平面再作第二个平面并与曲面相交,可得到第二条截线和它的曲率半径R2,用 R1与R2可表示出液体表面的弯曲情况。
若液面是弯曲的,液体内部的压力p1与液体外的压力p2就会不同,在液面两边就会产生压力差?P= P1- P2,其数值与液面曲率大小有关,可表示为:在数理方程中,拉普拉斯方程为:?u=d^2u/dx^2+d^2u/dy^2=0,其中?为拉普拉斯算子,此处的拉普拉斯方程为二阶偏微分方程。
三维情况下,拉普拉斯方程可由下面的形式描述,问题归结为求解对实自变量 x 、 y 、 z 二阶可微的实函数φ :上面的方程常常简写作:或其中div表示矢量场的散度(结果是一个标量场),grad表示标量场的梯度(结果是一个矢量场),或者简写作:其中Δ称为拉普拉斯算子 .拉普拉斯方程的解称为调和函数。
如果等号右边是一个给定的函数 f ( x , y , z ),即:则该方程称为泊松方程。
拉普拉斯方程和泊松方程是最简单的椭圆型偏微分方程。
偏微分算子或Δ(可以在任意维空间中定义这样的算子)称为拉普拉斯算子,英文是 Laplace operator 或简称作 Laplacian 。
拉普拉斯方程的狄利克雷问题可归结为求解在区域 D 内定义的函数φ,使得在 D 的边界上等于某给定的函数。
为方便叙述,以下采用拉普拉斯算子应用的其中一个例子——热传导问题作为背景进行介绍:固定区域边界上的温度(是边界上各点位置坐标的函数),直到区域内部热传导使温度分布达到稳定,这个温度分布场就是相应的狄利克雷问题的解。
拉普拉斯方程的诺伊曼边界条件不直接给出区域 D 边界处的温度函数φ本身,而是φ沿 D 的边界法向的导数。
数学物理方法课件:6-拉普拉斯变换
[ e p f2 ( )d ]e p f1( )d f1( p) f2 ( p)
00 15
例 在LR串联电路中加上一方形脉
冲电压E
E(t)
0E,0 ,
t
0
T
t
T
E (t )
求电路中的电流 i (t),设 i (0)=0。
解
L di Ri E (t) dt
(1)
由(2)得 I ( p) 1 E( p)
f(t) f(t-t0)H(t-t0)
o
t0
t
14
(7)卷积定理 L [ f1(t) f2 (t)] f1( p) f2 ( p).
其中 L [ f1(t)] f1( p), L [ f2 (t)] f2 ( p),
t
τ
f1(t) * f2 (t) 0 f1( ) f2 (t )d
2. Laplace 变换即(6.1.3)式存在的条件
(1)在 0 t < 的任一有限区间上,除了有限个第一类间 断点外,函数 f(t) 及其导数是处处连续的,
(2) 存在常数 M>0 和 0,使对于任何t (0 t < ), 有
| f (t) | Me t
的下界称为收敛横标,以0 表示。大多数函数都满足这 个充分条件
L
L0
E0
R E0
R
Rt
(1 e L ),
RT
Rt
(e L 1)e L ,
0t T t T
16
本节作业: 第95页 (1,2,4)
17
§6.2 Laplace 变换的反演
反演:由像函数求原函数
(一)有理分式反演法
若像函数
f ( p) G( p) H ( p)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以显然有
所以
下面对 的取值情况进行讨论
当 时
由拉普拉斯变换的位移性质可得
当 时
由于
因此
3、积分方程
若 ,则有
代入原方程得
对上式做拉普拉斯变换可得
解得
若令
则
所以
因为
所以
1、卷积公式
若 ,则
2、变换公式
1
拉普拉斯变换的应用
1、常微分方程
由拉普拉斯变换的导数性质可知
因此,直接对上述微分方程等式两边进行拉普拉斯变换可得
由此解得
其中
所以
因此
其中
2、偏微分方程
此处为便于求解,直接令
对上述方程等号两边做拉普拉斯变换(对t做)可得
上式是一个关于z的二阶常微分方程,令
因此
所以方程的通解为
拉普拉斯变换(12.04)
若 (即 时, ),关于复数 的函数
就称为 的拉普拉斯变换/,且
称为 的拉普拉斯逆变换。
拉普拉斯变换的几个重要性质( )
1、位移性质
对于任意 都有
2、压缩性质
对于任意 都有
3、导数性质
若函数f在 上k阶可导,且 ,则
4、积分性质
5、乘多项式性质
若 ,则
6、卷积性质
若 ,则
拉普拉斯变换的几个重要公式
