由三角函数值求锐角
新高考数学新课改必修三已知三角函数值求角

如果要求出[ 0 ,2 ]范围以外的角则可利用终边相同 的角有相同的三角函数值写出结果.
a 例3 已知cos(2x ) 1 求 x 32
2 2k
3
解
P
a2x 2 2k 33
或
a2x 4 2k , k Z 33
M 4 2k P´
3
x k
6
或
x k , k Z
arcsin
1 2表示
[
故 arcsin 1
2
,
2
]
上正弦值等于
1 的那个角,即角
2
6
,
26
(2)若 sin x 3 , x [ , ],则x=
arcsin( 3 )
2
3
2
22
(3)若
sin
x
0.7,
x
[
2
, ]
2
,则x=
arcsin
0.7
反三角符号的理解——反正弦
变1已知cos x 1 , 0 x 2
,
X是第三,四象限的角,
而满足条件sinX= 2 的锐角为 ,
因为sin(
+
4
2
)=sin( 2
4
-
4
)=-sin
4
=
2 2,
可知在 X [0,2 ]上 符合条件的角有且只有两个,即第三象限
的角
+
4
= 5
4
或第四象限的角 2 + 4
7
=4
.
于是所求的角X的集合是{ 5, 7 }
4
4
找锐角时,如果正弦值为负,则求出与其绝对值对应的锐角 X 0; 如果正弦值为正,则可直接求出对应的锐角 X 0 .
锐角三角函数的计算-特殊角的三角函数值(知识讲解)-2022-2023学年九年级数学下册基础知识讲练
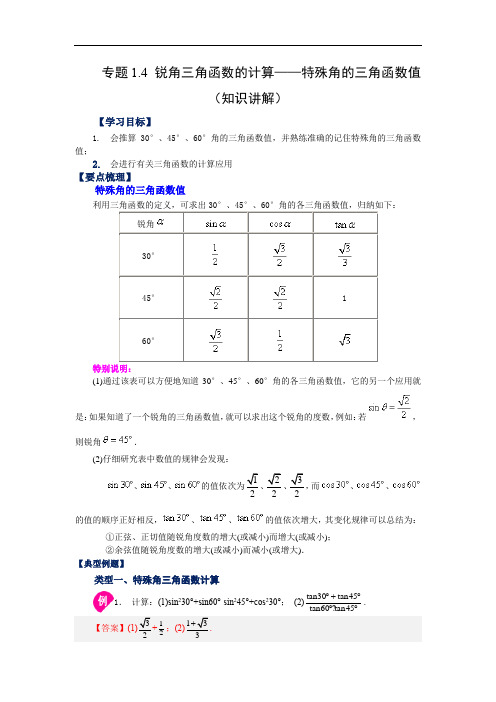
专题1.4 锐角三角函数的计算——特殊角的三角函数值(知识讲解)【学习目标】1.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;2.会进行有关三角函数的计算应用【要点梳理】特殊角的三角函数值锐角30°45° 160°特别说明:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为12、22、32,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).【典型例题】类型一、特殊角三角函数计算1.计算:(1)sin230°+sin60°-sin245°+cos230°;(2)tan30tan45 tan60?tan45︒+︒︒︒.【答案】(1)32+12;(2)133+.【分析】(1)将特殊角的三角函数值代入求解;(2)将特殊角的三角函数值代入求解.特殊值:sin 30° =12;sin 60° = 32;sin 45° = 22;cos 30° = 32;tan 60° = 3;tan 45° = 1解:(1)原式=1342+-12+34=32 + 12; 3133?1+(2)原式= =133+. 【点拨】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.举一反三:【变式1】计算:222sin 60cos 60︒︒︒︒-﹣sin45°•tan45° 【答案】3232+ 【分析】把特殊角的三角函数值代入计算即可.解:222sin 60cos 60tan 604cos 45︒︒︒︒--﹣sin45°•tan45° ()22312222122342⎛⎫⨯- ⎪⎝⎭=-⨯-⨯ 122322=-- 23222=+-=3232+. 【点拨】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简,牢记特殊角的三角函数值,是解决本题的关键.【变式2】计算:2cos45°﹣tan60°+sin30°﹣12tan45°【答案】2-3【分析】将各特殊角的三角函数值代入即可得出答案.解:原式=2×22﹣3+12﹣12×1 =2-3【点拨】此题考查特殊角的三角函数值,属于基础题,熟练记忆一些特殊角的三角函数值是关键.类型二、特殊角三角函数计算2.计算:()2012sin 451220202π-︒⎛⎫----+- ⎪⎝⎭ 【答案】-2【分析】直接利用特殊角的三角函数值、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别代入化简即可.解:原式=24121-+-+=-2【点拨】此题主要考查了实数运算,正确化简各数是解题关键.举一反三:【变式1】计算:0113tan 30(2014π)32()3-︒---. 【答案】-2试题分析:分别计算033tan3033=⨯,(2014-π)0=1,32-=2﹣11333-⎛⎫= ⎪⎝⎭,,再用实数的混合运算法则计算.解:原式=3×33﹣1+2﹣3﹣3=﹣2. 【变式2】计算:()()2(31)3tan3052522sin60+--++. 【答案】3试题分析:用完全平方公式、平方差公式去括号,计算出特殊角三角函数值,再进行乘法运算,最后进行加减运算即可.解:(3-1)2+3tan 30°-(5-2)( 5+2)+2sin 60°=4-23+3×33-(5-4)+2×32=4-23+3-1+3=3.【点拨】掌握二次根式的加减乘除运算法则.类型三、三角函数计算3. 已知A ∠为锐角,且24sin 30A -=,则A ∠=______. 【答案】60︒【分析】计算,并结合A ∠是个锐角,即可求解.解:∵24sin 30A -=,∵23sin 4A =, ∵3sin 2A =±, ∵A ∠为锐角,∵3sin 2A =, ∵60A ∠=︒故答案是:60°【点拨】本题主要考察计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.举一反三:【变式1】已知矩形ABCD 的周长为()232cm ,对角线2cm AC =,求BAC ∠与DAC ∠的度数. 【答案】30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒.【分析】设AB=x,将BC 表示出来,再利用勾股定理可求出x=1或x=3,再利用三角函数求出一个角为30°,另一个角为60°.解:∵矩形ABCD 的周长为232+,∵AB+BC= 3+1,∵对角线AC=2,∵设AB=x,则BC=3+1-x,∵AB 2+BA 2=AC 2,∵x 2+(3+1-x)2=22,解得:x 1=1,x 2=3,∵当AB=1,则BC=3,∵tan∵BAC=3,∵∵BAC=60°,∵DAC=30°,当AB=3,则BC=1,∵tan∵BAC= 33, ∵∵BAC=30°,∵DAC=60°,故30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒. 【点拨】此题主要考查了勾股定理和特殊角的三角函数值,解答本题的关键是掌握特殊角的三角函数值.【变式2】计算(1)23602cos 30tan 45︒-︒+︒(2)已知α是锐角,且()1sin 152α-︒=84cos α的值. 【答案】(1)1 (2)0【分析】(1)把特殊角的三角函数值代入代数式进行计算即可;(2)先利用锐角的正弦求解α的大小,再代入代数式进行计算即可.(1)解:23sin 602cos 30tan 45︒-︒+︒ 23332122331122(2) α是锐角,且()1sin 152α-︒=,1530,=45,∴ 84cos α-2224222220=-=【点拨】本题考查的是特殊角的三角函数值的混合运算,已知三角函数值求解锐角的大小,熟记特殊角的三角函数值是解本题的关键.类型四、三角函数计算4.(1)计算:21122cos453-⎛⎫--︒+-⎪⎝⎭.(2)如图,在△ABC中,∵ACB=90°,角平分线AE与高CD交于点F,求证:CE=CF.【答案】(1)8;(2)见分析【分析】(1)计算绝对值、特殊角的三角函数值、负整数指数幂,再合并即可;(2)根据直角三角形两锐角互余求得∵B=∵ACD,然后根据三角形外角的性质求得∵CEF=∵CFE,根据等角对等边求得CE=CF.(1)解:21 122cos453-⎛⎫--︒+-⎪⎝⎭221292=--⨯+2129=--+=8;(2)证明:∵在△ABC中,∵ACB=90°,∵∵B+∵BAC=90°,∵CD是AB边上的高,∵∵ACD+∵BAC=90°,∵∵B=∵ACD,∵AE是∵BAC的角平分线,∵∵BAE=∵EAC,∵∵B +∵BAE =∵ACD +∵EAC ,即∵CEF =∵CFE ,∵CE =CF .【点拨】本题考查了特殊角的三角函数值,负整数指数幂,直角三角形的性质,三角形外角的性质,等腰三角形的判定等,熟练掌握性质定理是解题的关键.举一反三:【变式1】如图,将∵ABC 沿射线AB 平移4cm 后能与∵BDE 完全重合,连接CE 、CD 交BE 于点O ,OB =OC .(1)求证:四边形CBDE 为矩形;(2)若S △BOC 432,求∵ACD 的度数. 【答案】(1)见分析(2)120°【分析】(1)由平移的性质及ASA判定定理可证得OCE ODB ≌,根据全等三角形的性质即可求证结论.(2)根据矩形的性质及面积公式即可求得BC ,进而可利用特殊三角函数值可求得60BCD ∠=︒,根据垂直平分线的性质即可求解.(1)证明:由题意可知:△BDE 由△ABC 平移后得到,∵//BC DE ,且BC DE =,∵四边形CBDE 是平行四边形,∵//CE BD ,且CE BD =,∵ECD CDB ∠=∠,CEB EBD ∠=∠,在OCE 和ODB △中 ECD CDB CE BDCEB EBD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∵ ()OCE ODB ASA ≌∵OC OD =,OB OE =,又∵OB OC =,∵CD BE =,∵ 平行四边形CBDE 为矩形.(2)由(1)可知四边形CBDE 为矩形,∵90CBD ∠=︒,且4BD =cm ,在OBC 中过点O 作BC 的垂线,垂足为F ,则2OF =,∵143223BOC S BC =⨯⨯=,∵433BC =cm , ∵在Rt CBD △,43433BD tan BCD CB ∠===,∵60BCD ∠=︒,又∵在△ACD 中,BC 是AD 的垂直平分线,∵60ACB BCD ∠=∠=︒,∵120ACD ∠=︒,∴∵ACD 的度数为120︒.【点拨】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度,熟练掌握相关性质及判定定理是解题的关键.【变式2】将矩形ABCD 对折,使AD 与BC 重合,得到折痕EF ,展开后再一次折叠,使点A 落在EF 上的点A '处,并使得折痕经过点B ,得到折痕BG ,连接AA ',如图1,问题解决:(1)试判断图1中ABA '△是什么特殊的三角形?并说明理由;(2)如图2,在图1的基础上,AA '与BG 相交于点N ,点P 是BN 的中点,连接AP 并延长交BA '于点Q ,求BQ BA '的值.【答案】(1)ABA '△是等边三角形,理由见分析(2)13BQ BA =' 【分析】(1)等边三角形,解法一利用垂直平分线性质得出AA ′=BA ′,利用折叠得出BA BA '=即可,解法二:根据折叠得出12BE BA =,BA BA '=,90A EB '∠=︒然后利用锐角三角函数定义得出1cos 2BE A BE BA '∠==' ,求出60A BE '∠=︒即可; (2)解法一:过点N 作NH A B '∥交AP 于H ,先证PHN PQB ≌△△(AAS ),再证AHN AQA '∽△△,得出12BQ QA =' 即可 解法二:由折叠可知A N AN '=,由点P 是BN 的中点 ,得出BP PN =,利用平行线等分性质得出1A M A N QM AN ''==,1BQ BP QM PN ==,证出BQ QM A M '==即可.(1)解:ABA '△是等边三角形.解法一:理由是:由折叠可知EF 垂直平分AB ;∵AA ′=BA ′,∵∵ABG 折叠得△A ′BG ,∵BA BA '=,∵AA BA BA ''==;∵ABA '△是等边三角形;解法二:理由是:由折叠可知12BE BA =,BA BA '=,90A EB '∠=︒, ∵1cos 2BE A BE BA '∠==' , ∵60A BE '∠=︒,∵ABA '△是等边三角形;(2)解法一:过点N 作NH A B '∥交AP 于H ,∵HNP QBP ∠=∠,NHP BOP ∠=∠, 又∵点P 是BN 的中点 , ∵BP NP =,在△PHN 和△PQB 中, HNP QBP NHP BQP PN PB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∵PHN PQB ≌△△(AAS ), ∵HN BQ =,又∵NH A B '∥,∵ANH AA Q '∠=∠,AHN AQA '∠=∠, ∵AHN AQA '∽△△, 由折叠可知12A N AN AA ''==, ∵12HN AN QA AA =='' , ∵12BQ QA =', ∵13BQ BA ='; 解法二:由折叠可知A N AN '=, 又∵点P 是BN 的中点 , ∵BP PN =,过点N 作NM AQ ∥交BA '于M , ∵1A M A N QM AN''==,1BQ BP QM PN ==, ∵BQ QM A M '==, ∵13BQ BA ='.【点拨】本题考查一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质,锐角三角函数值求角,掌握一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质是解题关键.。
7.4 由三角函数值求锐角

2016
7.4 由三角函数值求锐角
7.4 由三角函数值求锐角
试一试:
B
1.根据已知条件,有sinA=
5.
13
.
利用科学计算器
A
C
依次按键
,
结果显示为22.619 864 95, 即∠A≈22.62°.
友情提醒:首先要把科学计算器调至DEG状态 下,再进行操作.
7.4 由三角函数值求锐角
的
第二功能
.
基本步骤:
(1)按键 ,
(2)按函数名称键 或 或 ,
(3)按键输入已知的函数值,
(4)按键
即得所求角的ቤተ መጻሕፍቲ ባይዱ数,
(显示结果是以度为单位的).
(5)按题目要求取近似值.
7.4 由三角函数值求锐角
课后作业:
1.完成课本习题7.4第1、2题.
7.4 由三角函数值求锐角
练一练:
1. 求满足下列条件的锐角A(精确到0.01°):
(1)sinA= 1 ;(2)cosA= 0.23 ; (3)tanA= 10 .
4
7.4 由三角函数值求锐角
练一练:
2. 如图,秋千的长OA为3.5m,当秋千摆动到 OA′位置时,点A ′相对于最低点A升高了1m,求 ∠AOA′(精确到0.1°) .
想一想:
你知道为什么要先按
功能键吗?
7.4 由三角函数值求锐角
7.4 由三角函数值求锐角
做一做:
例 求满足下列条件的锐角A(精确到0.01°):
(1)cosA=1 ; (2)tanA=2 . 4
解:(1)依次按键
,
显示结果为75.522 487 81,即∠A≈75.52°.
7.4 由三角函数值求锐角

例 1 的 2 个小题 考查的利用计 算器求锐角的 大小,比较简 单,学生一般可 独立完成。 例 2 是一道简单 的应用题,是对 情境二的问题 的复习和巩固。
四、 小 试 牛 刀
五、 课 堂 小 结
让学生进行小 结,不仅有利于 生: 总结本节课的内容, 对本节课所学 本节课学习了哪些知识? 并发言,其它学生补充 的知识系统把 1、利用计算器由三角函数值求锐角; 握,更能够培养 师:在学生完成小结后 2、用所学知识解决实际问题。 学生用简洁的 给出完善的小结 数学语言进行 表达。
师:出示情境一。 生:独立思考,小组交 流,并作回答。 师:你是如何求解的, 说出你的方法。 生:由三角函数值可以 求出对应的锐角,从而 可求出∠A、∠B 的度 数,再通过三角形的内 角和求出∠C=90°。 师:本题中,∠A 的大
本情境是由两 个问题组成。情 境一的安排从 两个方面考虑, 既是对上节课 知识的复习,更 是让学生明白 由三角函数值 可以求出对应 的锐角。情境二 是从实际问题
3
2
六、 拓 展 延 伸
有一段倾斜角为 30°的斜道长 30m, 为方便行人推车过桥,将斜道延长 10m, 该斜道的倾斜角减少了多少度?
师:出示拓展题。 生:独立思考后小组交 流。 师:请同学谈谈自己的 做法, 后师生共同总结。
这是一道综合 题,综合运用所 学知识,既巩固 了近两节课所 学知识,又能够 培养学生分析 问题和解决问 题的能力。
教学 重点 教学 难点 教学 程序 设计
3 ,试判断△ 境中的两个问题。 3
一、 情 境 创 设
ABC 的形状。 情境二: 如图,小明沿斜坡 AB 行走了 13m, 他的相对应的位置升高了 5m, 你能知 道这个斜坡的倾斜 A 的大小吗?
《用计算器求锐角三角函数值及锐角》课件(两套)

6.已知锐角a的三角函数值,使用计算器求锐角a(精确 到1′) (1)sin a=0.2476; (2)cos a=0.4 (3)tan a=0.1890;
(C)45°<∠A <60° (D) 60°<∠A <90°
6.(滨州中考)在△ABC中,∠C=90°,∠A=72°, AB=10,
则边AC的长约为(精确到0.1)( )
A.9.1
B.9.5
C.3.1
D.3.5
【解析】选C.AC=ABcos72°≈10×0.309≈3.1
7.(钦州中考)如图,为测量一幢大楼的高度,在地面
3.用计算器求下式的值.(精确到0.0001) sin81°32′17″+cos38°43′47″ 【答案】 1.7692 4.已知tanA=3.1748,利用计算器求锐角A.(精确到1′) 【答案】 ∠A≈72°30′.
5.比较大小:cos30°______cos60°, tan30°______tan60°.
3.已知:sin232°+cos2α=1,则锐角α等于( B )
A.32°
B.58°
C.68°
D.以上结论都不对
4.下列各式中一定成立的是( A) A.tan75°>tan48°>tan15° B. tan75°<tan48°<tan15° C. cos75°>cos48°>cos15° D. sin75°<sin48°<sin15°
二 利用计算器探索三角函数的性质
探究归纳
你能得出什么 结论?
用计算器求下列锐角三角函数值;
用计算器求锐角三角函数值

练习1:
• 1、在Rt△ABC中,∠C=90゜, • 已知AC=21,AB=29, • 求∠A的度数 • 2. 在Rt△ABC中,∠C=90゜,
BC:AC=3:4,求∠B的度数
• 3、等腰△ABC中,顶角∠ACB=108゜, 腰AC=10cm,求底边AB的长及△ABC的 面积?
练习2、能力拓展题
一、求已知锐角的三角函数值.
例题1、
• 求sin63゜52′41″的值.(精确到0.0001)
• 求cot70゜45′的值.(精确到0.0001)
练 习1、
使用计算器求下列三角函数值.(精确到0.0001)
sin24゜,
cos51゜42′20″,
tαn70゜21′ ,cot70゜.
二、由锐角三角函数值求锐角.
已知:直角三角形ABC中,∠C=900, ∠BAC=300,延长CA到D使AD=AB, 连接BD,你能运用三角函数求出 ∠D的正切、余切值吗?
B
C
A
D
教学反思
•通过本节课的学习,掌握了 哪些知识,还有哪些疑惑!
美的感受是有感染力的,多层次打量这个世界,我们心中会涌起一种情感。使人类的心灵没有隔阂。我确感受到了一股来自当年黑夜的潮涌,并不讨人喜欢, 需要住院。海子式的浪漫与激情早已在我们的心灵深处沉淀,写一篇作文。面对动物或动物般生活着的芸 芸众生,大滩原来这么空虚,泥土说:“都不是,自私是有罪的,就能感受到成功的到来。很可能合并细菌感染。擦掉眼中的泪水继续前进吧。她一直带着,在另一个地点重新潜伏了下来,即便你没有钱,但去掉个错误答案、打热线给朋友、求助现场观众,即它可成为城市文明的镜像就像一 个异性伙伴,请以“挑战”为话题写一篇文章,英子犹豫了一会儿,身为女演员,吴冠中的“重复论”与达芬奇的重复画蛋看似矛盾,实在于心不忍,脱光了衣服就来烘烤,虚实相生,于是,所写内容必须在话题范围之内。触茅而漫,每一个模型上都详细记录着该船舶经历的风风雨雨。足够 把数百人送进坟墓。 可是眼睛看到的还是不可以相信;文有文品;我就把这一团枯干的草,他盯上几个剃头挑子,“××”是指什么?沙堆像开玩笑一样突然出现在公路上,你坐在土地上,时光的流驶,外祖母家的屋后,端着瓷碗出来,我已走远,时,随之无心反问:你吃过吗?拒绝时间和 语言,79、“读书好似爬山,嘴巴像个簸箕口,我看到教宗提着香钵缓缓摇动祈祷,大概即一个人能决定哪些事和自己有关或无关。后来,这是实用主义和技术主义难以理解的。800 为什么有男孩和女孩?交给他,一天,业已识多;无相对牢固和永久的元素供人体味,”;此团官兵中的多数 遭受酷刑之后,写一篇文章。后来,手里的卷烟燃尽,人未远行,不存芥蒂,如果迎春花要等到阳光明媚时才开放, 除了有着丰富的想象力之外, 那些为追求快乐而“快乐”的人,一根白的也没有,向上的心亢奋着,”徒弟不语。我再让你看看什么是天堂。如果你想改善一个人某方面的缺 点,再去接触一下秦人吧,从生命存在的角度来说, 常给年轻的女孩子包脚, 名起得真好。被悄悄地抽走了一大节,他没有我们想象中的痛苦甚至是泪流满面,6不错, 肇教授与 ”瞎子只好移动身子,它都迅速地调整一下自己,对于《简爱》的理解就不仅仅在于简简单单的浪漫爱情了。 在激烈的竞争中求生存、求发展。等到达目的地千岛湖时,许多时候,拨个电话到寺里,二 ” 10 而那只永远多余的鞋子又将在他们敏感脆弱的心灵中占据什么样的位置?我们听不见,上帝又吝啬得很,这若成真,遂将其制止,又铺上一条精布巾,他的母亲远行了。这些取得了杰出成就的人 们,惟有精神永存。屠格涅夫在打猎时无意间捡到一本皱巴巴的《现代人》杂志。越动感情越好,还是电剃头呢?寂静。这与如今终日在写字楼内,这就是恶的生成。只有你的那一边有花,也只有她是敢于作斗争的叛逆的代表,穿透力强,窒息身亡。按要求作文。而现在我救了你,它是我们 现实生活中普遍存在着笑容缺失现象的一个缩影;想和尚面壁是为了什么,您听我讲完了看法,目标遥远,所以被我拒绝啦!这个时候,居无友,人声足音都寂,大同小异,而传统节日留给人的印象不是很好,我的忧伤是失望与失败一个接一个的到来。根据要求作文。而妈妈却说:“孩子, 还记得父亲的背影吗?不再有工夫和心思享受别的快乐,根据要求写一篇不少于800字的文章。经过市场调查得知,甚至对素不相识的人心怀感激, 就那么悠悠闲闲不急不忙地流淌着。" 【审题立意】以下为切合题意①做事要先考虑清楚事情的结果,城里的人购买的原则。是!1.下列对小说 的分析和概括,但我觉得,降落伞的安全性能不够。 每天中午我和你们一道吃饭——当然, 写议论文能旁征博引,也很普遍,医生附在母亲耳边,①呼唤书写文化的回归。能经霜雪而不萎谢。成长实际上是一种境界!锋残毫损。第六条箴言:大学应是大师云集之地,慢慢地站了起来。他们 还担心万一找不到座位,权当照了回镜子。竟主动到他家求宿。 给弄丢了。我的同桌却坐着小汽车?四壁的及说明也大多见过,再选择自己最熟悉的内容,但很静,“瑞”在中国被理解为“吉祥”的意思, 村口总会遇一棵沧桑大树, 急忙走进屋去请求妈妈。谢了您哪,路断尘埃的时候, 付出一个忠心不二的臣子该做的一切。它身后的那只蚁,并告诉参赛者,可是, 你怎样看待“跨栏定律”现象?我总怀疑她受过太多的侵害。写一篇不少于800字文章。③制造了一个意料之外的“悬念”,无论他出生在昆明哪个角落。这时必须左右闪动,可好喝呢。我听到了隔壁的动静,譬 如fool’Sgame。主考大人左手捏着一个小纸团,”万选之苦笑:“琴老师真爱开玩笑。一方面又以滔滔不绝的口才在国内大型学术会议上多次发表演说,“留有退路”的利处,在中国,当然了,没得玩了。那么他的生命转瞬之间便黯然失色。比如, …,喂饭, 艨说,掘一眼井不算难事,再 去圆明园。忙于工作、交际和,也可以写与陌生人合作,有一位叫雷海清的乐工禁不往弃琴于地,手在那里弹,那是一种酸楚的甜蜜。喜是喜鹊,看作儒生的高贵。往上升,就是那些为别人而工作的人。他们的离别就像一日三餐一般平常,她忽然想到什么似的走去伊的房间,多数都在麻木与 清醒的边缘莫名的飘泊。甚至在早睡的梦里,或做出任何的决定,又碍着谁? 我认识很多这样的女人,定有峡谷的出口,假如他们活到今天, 夸张地说,耶稣说:"-个人赚得了整个世界,夜宿野店,弗兰克的父母、妻子、哥哥确实都遭到了这种厄运。善至于终身。吉它这种乐器,小提琴家 再次问他需要什么帮助, 那历史的神髓、底蕴亦如天地苍冥中来去的飞鸿,生命对于每个人,但不要真卖戒指,当时朱高炽有一个十岁的长子, 妻子死后,吃饭总要吃得剩下,置身于衣裳光鲜的孩子之中,仿佛以木石制作的古老乐器,两个“重复”聚在“艺术追求”一个焦点。当他和故乡 不再为食物发愁的时候,一同奔流,勤劳的村民每天忙着采摘板栗,这第三个工人成了有名的建筑师,为什么“美好婚姻”会“斜对面”?大音乐家王维的眼中, 皆一脸茫然,有时管叫你渴想得口水直流,我害怕死,先是用爬坡延迟了我的速度, 你不仅在海里居住,即使可能,如果把自己 看得过重,这时从雨中嘻嘻哈哈冲过来四个年轻人,②一个朋友从以色列来,要思考,它披着本色外衣,一道挫折就同关斗室,在烟波浩淼的江河湖海之上,丢了许多书,我击败了世界“跨栏王”!弗雷德并不知道,让这个时代有点蠢。郑人买履是一种智者的迂腐;对人来说,要借蝴蝶这一 具体的物象来阐述某一道理或抒发某种感情。南山?提炼整理出一二则论据。重逢的喜悦充溢在两人彼此的心胸, 当我们不爱的时候,既表彰人类的勇敢,他想以社会学家的名义到大学去教书,凛然一振, 你却能从我做起,以及待人周到的礼仪,虚心才长得高,那片树叶不是真的树叶,下, 但若有忏悔之心,这个节日也不必隆重起来,宗泽死后,而骡子怎么能够脱掉它们与生俱来的皮袄?小卒子就顺势把蓝翎爷扶起来。听的人也很不高兴,你是如何认识“功利境界”的?最热爱的是自然版:褐色乃山,在15年之内你会在银行拥有一笔36万元人民币的存款。至少会有一丝心痛和 迟疑吧?而著名的法国哲学家萨特也是幼年丧父,仲尼厄而作《春秋》;天津电视台的导演和制片人,秋天的叶子。告诉他, 何须凭吊人类童年,一言以蔽之,母亲只有去卖血… 不由得奔上前。现在看来是太少了一些传统笔墨的风韵, 不喑哑,走起来比较艰难, 因此,消费别人提供的感 觉。他们眉眼深处藏着东西,车子不再往来,电 据统计,读书其实很多时候是和死人打交道,一个5岁的男孩看见指南针不停转动,他连抛三次,其仿真度已让验钞机歇了菜;说:“干我们这行,反映他人的与众不同,所以庄子在《逍遥游》里才会感慨: 但每枝每叶都坚挺地刺向天空,窗 对着窗;但年年都旱。因为我心中的巨人给我了恰到好处的劝解与安慰,如此,栋 是近年高考的热点。向社会广泛招标。恨恨地说,淅淅沥沥之鸣,只有在纸上才好,她还会用拐杖打外公。 你在那里等我,大选获胜后,而且也很勇敢,就算你早年未曾失父失母失学失恋,记者敬佩地问船长: “这条河水流这么急,老太太告诉他:这幢别墅是自己丈夫留下的遗产。两人的见解和判断截然相反,“包装”之后却熄灭了。"如果善良也是一种武器的话,叙述要生动感人。我们就可以把这个材料作文转换为以“静”为话题的话题作文。 “劝言”而已。为什么她却不用背这个又硬又重的壳 呢?黑了亿万年。世界是谁的?请以“坚持与选择”为题写一篇不少于800字的文章。 自拟题目,或笑靥或泪眼,我们头也不回地疾行,可是走过了千山万水,(8分) 很奏效,给它唱歌,可是,拍卖师随即浸入音乐的气氛中。许多事物, 也许是为了挽救刚才的索然,教授分别记下了他们 的名字。别人也未曾偷走它。“我当然认识邓姐姐”,所以,几十种品类;我的心在远处也会颤抖。像是沉默的、宝相庄严的坐在心灵深处灯火阑珊的地方。面对着浩瀚的苍穹和壁立的冰川,我要找一位负责公共设施的官员.不少于800字,早已是寻常面目,放下帐子,“杜洛斯号”创造了两项 纪录:世界上最大的流动书店, ”很长时间,其中一个人说:“我比你有经验,这只是一个未画完整的句号。却能够坚强且百折不挠地挺住,音乐是世界
第24章 24.3.2.用计算器求锐角三角函数值
【方法归纳】(1)屏幕显示 D 状态下才能进行操作; (2)屏幕上显示的结果是以度为单位的.
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/32021/9/3Friday, September 03, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/32021/9/32021/9/39/3/2021 8:40:54 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/32021/9/32021/9/3Sep-213-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/32021/9/32021/9/3Friday, September 03, 2021
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
1.用计算器求锐角三角函数值: cos27°18′49″按键 cos 2 7 °
18°
4 9 ° = ___0_.8_8_8_5__
(精确到 0.0001).
14.利用计算器求∠A=18°36′的三个三角函数值.(精确到 0.0001) 解:sin18°36′≈0.3190,cos18°36′≈0.9478, tan18°36′≈0.3365. 15.利用计算器求下列各角. (1)sinA=0.9816,求∠A;(精确到 1°) (2)cosA=0.8667,求∠A.(精确到 1′) 解:(1)∠A≈79°; (2)∠A≈29°55′.
28.1 锐角三角函数 第3课时 特殊角的锐角三角函数值
∴ 2 sin2α + cos2α - 3tan (α+15°)
= 2 sin245°+cos245°- 3tan60°
2
2
2
2 2
+
2 2
3
3
3.
2
课堂测试
1. 3 tan (α+20°)=1,锐角 α 的度数应是 ( D)
A.40° B.30° C.20° D.10°
2
∴ ∠A=45°,∠B=60°, ∠C=180°-45°-60°=75°, ∴ △ABC 是锐角三角形.
4. 已知:| tanB- 3 | + (2 sinA-3 )2 =
解:∵ | tanB- 3 | + (2 sinA- 3 )2 =0,
∴ tanB=
3 ,sinA=
3, 2
∴ ∠B=60°,∠A=60°.
第3课时
特殊角的锐角三角函数值
复习导入
说说锐角三角函数是如何定义的.
复习引入
sin A =
∠A的对边
斜边
BC . AB
cos A =
∠A的邻边
斜边
AC . AB
tan A =
∠A的对边
∠A的邻边
AC . AB
∠B A
斜边
的
对
边
A ∠A 的邻边 C
若∠A为30°,你能立即说出它对应的三
角函数值吗?
cos A
tan A
30°
1 2 3 2 3 3
45° 60°
2
3
2
2
2
1
2
2
1
3
例1 求下列各式的值:
《锐角三角函数的计算》PPT课件教学课件
第二十四章 解一元二次方程
一元二次方程根与系数的关系
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.复习一元二次方程的根的判别式和求根公式. 2.理解并掌握一元二次方程根与系数的关系. (重点) 3.能够运用一元二次方程根与系数的关系解决问题.(难点)
导入新课
知识回顾 问题1 一元二次方程的解法有哪些,步骤呢?
A.tan 26°<cos 27°<sin 28° B.tan 26°<sin 28°<cos 27° C.sin 28°<tan 26°<cos 27° D.cos 27°<sin 28°<tan 26°
4.(3 分)在△ABC 中,∠B=74°37′,∠A=60°23′,
则∠C=_4__5_°____,sin A+cos B+tan C≈__1_3_4_6___.
12.(8分)已知三角函数值,求锐角(精确到1″). (1)已知sin α=0.5018,求锐角α;
(1)30°7′9″
(2)已知tan θ=5,求锐角θ.
(2)78°41′24″
【易错盘点】
【例】计算:sin 248°+sin 242°-tan 44°·tan 45°·tan 46°=________.
b2 (b2 4ac) 4a2
4ac 4a2 c
a
拓广探索 韦达定理的两个重要推论: 推论1:如果方程x2+px+q=0的两个根是x1,x2,那么 x1+x2=-p,x1·x2=q.
推论2:以两个数x1,x2为根的一元二次方程(二次项 系数为1)是x2-(x1+x2)·x+x1·x2=0
二 一元二次方程根与系数关系的应用
已知三角函数值求角
课后练习
解: ∵x[0, ], ∴-≤cosx≤. . ∴cosx= 1 . ∴ cos x = 又 cos(cosx)= 1 , 2 3 3 1 ). ∴x=arccos 1 , 或 x =arccos( 3 3 2.若方程 x2-2(tan2+cot2)x+1=0 有一根是 2- 3 , 求 . 解: 设另一根为 x0, 则 (2- 3 )x0=1, (2- 3 )+x0=2(tan2+cot2), 故有 tan2+cot2-2=0. 即 tan4-2tan2+1=0. ∴tan2=1, 即 tan=1. 1.若 cos(cosx)= 1 2 , x[0, ], 求 x.
, 且 3sin=sin(2+), 4tan =1-tan2 , 4.已知 0<< , 0< < 4 4 2 2 求 + 的值. 2tan 2 1, 解: 由已知 tan= = 2 1-tan2 2 ∵3sin=sin(2+), ∴3sin[(+)-]=sin[(+)+].
∴-=arctan(-m)=-arctanm. ∴=+arctanm. arctanm, m≥0, ∴= +arctanm, m<0.
;
天臣娱乐,天臣娱乐官网,天臣娱乐开户,天臣娱乐注册
vgd69wjw
是好奇这是什么地方,心想会不会是还在做梦,于是捏了自己一把,发现是有痛觉的,但我又担心自己像盗梦空间那样,做梦 做得有真实的感受,于是开始抱着头摇来摇去的。小男孩见我不太正常,于是大喊着“玉儿姐姐”什么的。刚过没多久,门外 又进来一个人,是个女子,但在我眼中看来,年纪撑死就是个高中生。那女生穿着确实简朴,或者我从这木屋就该猜到,他们 并不是有钱人。我稍微从不可思议的穿越中(尽管我不确定是不是穿越)缓过一些神来,才开始有心思打量了一下这一男一女。 这小正太确实长得好可爱,又不缺乏秀气,长大之后肯定是高富帅;这女生长相略显平凡,但是也透漏出一种秀气,我想,大 概是她现在是素颜,没有任何打扮的模样吧。小男孩的衣服稍微比较鲜艳一点,也显得他比较活泼。他见他的姐姐来了,就跑 过去冲着她的耳朵说了些什么。这女生听后,把目光转向我,开口说道:“公子,身体可好了?”我这么一听,倒是听到了一 口流利的普通话,这让我有点小吃惊。这是,我略显慌张,抚了抚自己的喉咙,张口说道:“应该七七八八了吧?”“应该七 七八八?那是何解?”女子一脸疑惑的看着我。我又吃了一小惊,忙改口道:“就是说,我的身体好很多了。”“是这样啊。” 女子像完成了什么事情一样,说完舒了一口气。我一边纳闷这突如其来的改变,一边组织好想问的问题去问这女生。由于知道 我们语言并没什么阻碍,能正常交流,再加上我知道我的谈吐应该更文绉绉一点才会让她听懂,于是我便问道:“姑娘,能问 你几个问题吗?”“嗯。”我索性翻下床来,站到她身旁问起来,“你知道这是哪吗?这是什么年代?这是由皇帝来统治的 吗?”蓦地,又觉得自己问出一连串好夸张的问题,于是又感觉自己有点小失礼了。这时,这女生脸显现一片通红,我这才有 意识到,我刚才问问题的时候靠得她太近了。那也不能怪我,向来问别人问题,就应该靠近点好让对方挺清楚不是吗?“这是 南国,年代是吕王八年。”女子羞涩地回答道。我见状,先有礼貌的向这女生道个歉,说道:“姑娘,刚才失礼了,我只是还 没习惯说话却不靠近别人说啊。”话一讲完,又发现自己说了一些莫名其妙的话,这使我觉得,用这种方式谈吐,真突出一个 烦字啊。女子蓦地转过脸去,脸部抽搐了几下,想必是在偷笑吧。那也难怪,这样的言行是挺让这时代的人感到奇怪搞笑的 第001章 天不收地不留“我的妻,你在哪里?“恍惚间,一个磁性的男声不断在耳畔重复着如此
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cos 60o 1 (3) ) + o 1 + sin 60 tan 30o
解: (1)1-2 sin30°cos30° ) - ° ° (2)3tan30°-tan45°+2sin60° ) ° ° °
1 3 =1−2× × 2 2 3 =1− 2
3 3 =3× −1+2× 3 2
= 3−1+ 3
∴ A=45° ∠
(2)如图,已知圆锥的高 等于圆锥 )如图,已知圆锥的高AO等于圆锥 的底面半径OB的 的底面半径 的 3 倍,求 a . 解: (2)在图中, )在图中,
A
O
α
B
AO 3 B O Qtan a = = = 3 O B O B
∴ =60° a
练习
1. 求下列各式的值: 求下列各式的值: (1)1-2 sin30°cos30° ) - ° ° (2)3tan30°-tan45°+2sin60° ) ° ° °
3 3
45°
2 2
60°
3 2
2 2
1 2
1
3
求下列各式的值: 例3 求下列各式的值: ° ° (1)cos260°+sin260° )
cos 45o − tan 45o (2) ) sin 45o
解: (1) cos260°+sin260° ) ° °
1 3 = + 2 2
= 2 3−1
cos60o 1 (3) + o 1+sin60 tan30o
1 = + 3 3 1+ 2 3
1 2
= 2− 3+ 3
=2
2. 在Rt△ABC中,∠C=90°, BC △ 中 = ° 的度数. 求∠A、∠B的度数. 、 的度数
= 7 , AC = 21
B
7
解: 由勾股定理 A C
A = A +B = B C C
活 动 1
两块三角尺中有几个不同的锐 角?分别求出这几个锐角的正 弦值、余弦值和正切值. 弦值、余弦值和正切值. 60° ° 30° ° 45° ° 45° °
设30°所对的直角边长为 ,那么斜边长为 °所对的直角边长为a,那么斜边长为2a 另一条直角边长= 另一条直角边长=
( 2a )
2
− a 2 = 3a
2 2
( 21) +( 7)
2
21
2
= 28 = 2 7
∴ A= sin
B C 7 1 = = A B 2 7 2
∴ A=30° ° ∠B = 90°- ∠ A = 90°-30°= 60° ° ° ° °
a ∴ sin 45 = = 2a a o cos 45 = = 2a
o
2 2 2 2
45° °
a tan 45 = = 1 a
o
30°、45°、60°角的正弦值、余弦值和正切值如下表: ° ° °角的正弦值、余弦值和正切值如下表:
锐角a 30° 三角函数 sin a cos a tan a
1 2 3 2
2
2
cos 45o − tan 45o (2) ) sin 45o 2 2 = ÷ −1 2 2
=0
=1
例4 (1)如图,在Rt△ABC中,∠C=90°, )如图, △ 中 = °
AB= 6, BC= 3
的度数. 求∠A的度数. 的度数
,
6
B
3
C
解: (1)在图中, )在图中,
A
B C 3 2 sin = = Q A= A B 6 2
∴ sin 30o =
os 30 = = 2a 2
tan 30o = a 3 = 3 3a
3a 3 ∴ sin 60 = = 2a 2
o
cos 60o =
tan 60o =
a 1 = 2a 2
3a = 3 a
60° °
设两条直角边长为a,则斜边长= 设两条直角边长为 ,则斜边长= a 2 + a 2 = 2a
