2.3 连续型随机变量的数学期望与方差ppt课件
合集下载
《数学期望与方差》课件

相关系数的计算公式
相关系数在统计学、金融等领域有广泛应用,如股票价格与市场指数的相关性分析、回归分析等。
相关系数的应用
数学期望的性质
数学期望具有线性性质、可加性质、可乘性质等,这些性质在概率论和统计学中有重要应用。
05
数学期望与方差的实例分析
总结词
数学期望和方差在投资组合的风险与回报分析中具有重要应用。
总结词
利用数学期望和方差可以对赌博游戏的概率进行分析。
详细描述
在赌博游戏中,玩家需要根据游戏规则和概率计算每种可能结果的数学期望和方差,以评估游戏的风险和潜在收益。通过比较不同赌博游戏的数学期望和方差,玩家可以做出更明智的决策。
数学期望
对于赌博游戏而言,数学期望计算的是长期玩家的平均收益。如果数学期望为正数,则表示长期玩家将获得正收益;如果数学期望为负数,则表示长期玩家将面临亏损。
方差
在赌博游戏中,方差反映了玩家实际收益与预期收益之间的波动范围。较小的方差表示实际收益相对稳定,而较大的方差则表示实际收益可能存在较大的波动。
01
02
03
04
总结词:数学期望和方差可用于预测市场的表现。
THANK YOU
数学期望和方差在某些情况下可以相互转化,如当随机变量服从正态分布时。
变量同时变动的情况,即一个变量增加或减少时,另一个变量也相应地增加或减少的概率。
协方差的概念
协方差 = E[(X-E[X])(Y-E[Y])],其中E[X]和E[Y]分别是X和Y的数学期望,X和Y是随机变量。
协方差的计算公式
协方差可以用于分析投资组合的风险,如果两个资产的收益率呈正相关,则它们的协方差为正;如果呈负相关,则协方差为负。
协方差的应用
1
相关系数在统计学、金融等领域有广泛应用,如股票价格与市场指数的相关性分析、回归分析等。
相关系数的应用
数学期望的性质
数学期望具有线性性质、可加性质、可乘性质等,这些性质在概率论和统计学中有重要应用。
05
数学期望与方差的实例分析
总结词
数学期望和方差在投资组合的风险与回报分析中具有重要应用。
总结词
利用数学期望和方差可以对赌博游戏的概率进行分析。
详细描述
在赌博游戏中,玩家需要根据游戏规则和概率计算每种可能结果的数学期望和方差,以评估游戏的风险和潜在收益。通过比较不同赌博游戏的数学期望和方差,玩家可以做出更明智的决策。
数学期望
对于赌博游戏而言,数学期望计算的是长期玩家的平均收益。如果数学期望为正数,则表示长期玩家将获得正收益;如果数学期望为负数,则表示长期玩家将面临亏损。
方差
在赌博游戏中,方差反映了玩家实际收益与预期收益之间的波动范围。较小的方差表示实际收益相对稳定,而较大的方差则表示实际收益可能存在较大的波动。
01
02
03
04
总结词:数学期望和方差可用于预测市场的表现。
THANK YOU
数学期望和方差在某些情况下可以相互转化,如当随机变量服从正态分布时。
变量同时变动的情况,即一个变量增加或减少时,另一个变量也相应地增加或减少的概率。
协方差的概念
协方差 = E[(X-E[X])(Y-E[Y])],其中E[X]和E[Y]分别是X和Y的数学期望,X和Y是随机变量。
协方差的计算公式
协方差可以用于分析投资组合的风险,如果两个资产的收益率呈正相关,则它们的协方差为正;如果呈负相关,则协方差为负。
协方差的应用
1
随机变量的数学期望 ppt课件

概率论与数理统计
第一节 数学期望
离散型随机变量的数学期望 连续型随机变量的数学期望 随机变量函数的数学期望 数学期望的性质 课堂练习
ppt课件
2
在前面的课程中,我们讨论了随机变量及其分 布,如果知道了随机变量X的概率分布,那么X的 全部概率特征也就知道了.
然而,在实际问题中,概率分布一般是较难 确定的. 而在一些实际应用中,人们并不需要知 道随机变量的一切概率性质,只要知道它的某些 数字特征就够了.
分布为pij , i,j=1,2, …,则
E(Z) E[g(X ,Y )]
g(xi , y j ) pij
j1 i1
(2) 如果X、Y是连续型随机变量,联合概
率密度为f(x,y),则
E(Z ) E[g( X ,Y )] g( x, y) f ( x, y)dxdy
ppt课件
24
例4.6 设 ( X , Y ) 的分布律为
概率
1/6 3/6 2/6
一旅客8:20到车站,求他候车时间的数学期望.
ppt课件
12
解:设旅客的候车时间为X (以分计),其分布率为
X 10 30 50 70 90
pk 3 6
上表中例如
2 11 13 12 6 66 66 66
P{X 70} P(AB) P( A)P(B) 1 3 66
ppt课件
32
例10 设二维连续型随机变量(X ,Y)的概率密度为
f
( x,
y)
Asin( x
y)
0 x
2
0
其它
(1)求系数A, (2)求E( X ), E( XY ).
解:(1)由于
f
( x,
y)dxdy
第一节 数学期望
离散型随机变量的数学期望 连续型随机变量的数学期望 随机变量函数的数学期望 数学期望的性质 课堂练习
ppt课件
2
在前面的课程中,我们讨论了随机变量及其分 布,如果知道了随机变量X的概率分布,那么X的 全部概率特征也就知道了.
然而,在实际问题中,概率分布一般是较难 确定的. 而在一些实际应用中,人们并不需要知 道随机变量的一切概率性质,只要知道它的某些 数字特征就够了.
分布为pij , i,j=1,2, …,则
E(Z) E[g(X ,Y )]
g(xi , y j ) pij
j1 i1
(2) 如果X、Y是连续型随机变量,联合概
率密度为f(x,y),则
E(Z ) E[g( X ,Y )] g( x, y) f ( x, y)dxdy
ppt课件
24
例4.6 设 ( X , Y ) 的分布律为
概率
1/6 3/6 2/6
一旅客8:20到车站,求他候车时间的数学期望.
ppt课件
12
解:设旅客的候车时间为X (以分计),其分布率为
X 10 30 50 70 90
pk 3 6
上表中例如
2 11 13 12 6 66 66 66
P{X 70} P(AB) P( A)P(B) 1 3 66
ppt课件
32
例10 设二维连续型随机变量(X ,Y)的概率密度为
f
( x,
y)
Asin( x
y)
0 x
2
0
其它
(1)求系数A, (2)求E( X ), E( XY ).
解:(1)由于
f
( x,
y)dxdy
第一节数学期望ppt

0
0
xe x e x dx 1 e x 1
0
0
0
概率论
3) 正态分布 N(, 2)
概率论
X ~ f (x)
1
( x )2
e , 2 2 x
2
E( X ) x
1
( x )2
Z是一维随机变量,则
(1) 若( X ,Y )是二维连续型,
概率密度为f ( x, y), 则有:
E(Z ) E[g(X ,Y )] g(x, y) f (x, y)dxdy
(2) 若( X ,Y )是二维离散型,
概率分布为P{ X xi ,Y y j } pij (i, j 1, 2,
一般是比较复杂的 .
概率论
2. 定理: 设Y是随机变量X的函数: Y=g(X) (g是连续函数)
(1) 当X为离散型时,它的分布律为P(X= xk)=pk,
(k 1,2,),若 g( xk ) pk绝对收敛,则有
k 1
E( X ) xk pk
k 1
(2) 当X为连续型时,它的密度函数为 f (x), 若
pk (1 p)nk
n!
pk (1 p)nk
k1 k !(n k)!
k1 (k 1)!(n k)!
n
np
(n 1)!
pk1 (1 p)n1(k1)
k1 (k 1)!(n k )!
n1
令l k 1 np
C
l n1
p
l
(1
p)n1l
g( x) f ( x)dx绝对收敛,则有
连续型随机变量的数学期望与方差
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
数学期望与方差ppt课件

频率 nk n
2 13 15 10 20 30 90 90 90 90 90 90
试问:该射手每次射击平均命中靶多少环?
2
解
平均射中环数
射中靶的总环数 射击次数
0 2 113 2 15 3 10 4 20 5 30 90
0 2 1 13 2 15 3 10 4 20 90 90 90 90 90
P{ X xk } pk , k 1,2, .
若级数 xk pk 绝对收敛, 则称级数 xk pk
k 1
k 1
为随机变量 X 的数学期望, 记为 E( X ). 即
E( X ) xk pk .
k 1
5
2.连续型随机变量数学期望的定义
设连续型随机变量 X 的概率密度为 f ( x),
若积分
第一节 数学期望
一、数学期望的概念 二、数学期望的性质 三、随机变量函数的数学期望 四、小结
1
一、数学期望的概念
ห้องสมุดไป่ตู้
引例 射击问题
设某射击手在同样的条
件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下
命中环数 k 0 1 2 3 4 5
命中次数 nk 2 13 15 10 20 30
k
k
4. 设 X, Y 是相互独立的随机变量, 则有
E( XY ) E( X )E(Y ).
说明 连续型随机变量 X 的数学期望与离散型随 机变量数学期望的性质类似.
14
数学期望在医学上的一个应用
An application of Expected Value in Medicine 考虑用验血的方法在人群中普查某种疾病。集体做法是每 10个人一组,把这10个人的血液样本混合起来进行化验。如果 结果为阴性,则10个人只需化验1次;若结果为阳性,则需对 10个人在逐个化验,总计化验11次。假定人群中这种病的患病 率是10%,且每人患病与否是相互独立的。试问:这种分组化 验的方法与通常的逐一化验方法相比,是否能减少化验次数?
第三节课,第一章2. §2.3.连续型随机变量概念§2.4 数字特征

1
x α dx
1 α 1 x C α 1
2
3 1
0.9
1 0.972 0.028
7
答: 供电量不足的概率为0.028 .
典型问题——求概率密度中参数 例2. 设连续型随机变量 X 的概率密度 (x)为:
cx 2 0 x 1 ,求常数c的值. ( x) 其他 0
即:E(C) = C , D(C) = 0
(2) 变量和的期望与方差等于它们期望与方差的和;
即:E(X+Y) = E(X)+E(Y) , D(X+Y) = D(X)+D(Y) (3)常量因子可以提到期望外面. 即:E(kX) = kE(X) (4)常量因子平方可以提到方差外面. 即:D(kX) = k2D(X)
例5. 若 D( X ) 2, 则D(2 X 5) __
解: 随机变量的期望与方差的性质
D( 2 X 5) D(2 X ) D(5)
(2)2 D( X ) 0 4 2 8
18
作
业:
74页2.01、2.02、2.04、2.05、2.06、2.08 题 74页2.09题、 2.10题、 2.14题、 2.16题、2.17题
方差D(X)等于X平方的数学期望减数学期望平方.
80 13 2 80 169 D( X ) ( ) 16 6 16 36
14
典型问题—求连续型随机变量的参数 例3. 设连续型随机变量 X 的概率密度为 a bx2 0 x 1 3 ( x) ,若数学期望E ( X ) 5 其他 0 求: 常数 a, b的值 解: 因为有两个未知参数, 所以需要建立两个方程 根据概率密度 (x)性质 ( x )dx 1
常见的连续型随机变量

第五节 常见的连续型随机变量
7
例 1(续)
所以,
PB P10 X 15 P25 X 30
P40 X 45 P55 X 60
15
1 dx 30
1
45
dx
1
60
dx
1
dx
10 60
25 60
40 60
55 60
1 3
.
第五节 常见的连续型随机变量
8
例2
设随机变量 服从区间 3, 6上的均匀分布,求方程
上的均匀分布.
第五节 常见的连续型随机变量
6
例 1(续)
其密度函数为
f
x
1 60
0
0 x 60
其它 .
令 B 被带往甲地 .
开往甲地汽车的到达时间:
7:00, 7:15, 7:30, 7:45, 8:00; 开往乙地汽车的到达时间:
7:10, 7:25, 7:40, 7:55, 8:10.
k!
k 0, 1, , n, .
设随机变量T 的分布函数为 FT t .
则当 t 0 时, FT t 0 ;
第五节 常见的连续型随机变量
18
例 4(续)
当 t 0时, FT t PT t 1 PT t
1 P在长度为 t 的时间间隔内随机事件 A 没发生
1 PX 0 1 et .
4x2 4 x 2 0
有实根的概率.
解:
由于随机变量 服从区间 3, 6上的均匀分布,所以
的密度函数为
f
x
1 9
0
3 x6
其它 .
第五节 常见的连续型随机变量
9
例 2(续)
概率论与数理统计PPT课件第四章数学期望与方差

回归分析
在回归分析中,数学期望和方差 等统计指标用于描述因变量和自 变量之间的关系,以及预测未来
的趋势。
假设检验
在假设检验中,数学期望和方差等 统计指标用于比较两组数据或样本 的差异,判断是否具有显著性。
方差分析
方差分析利用数学期望和方差等统 计指标,分析不同组别或处理之间 的差异,确定哪些因素对数据变化 有显著影响。
质量控制
统计分析
在统计分析中,方差分析是一种常用 的统计方法,通过比较不同组数据的 方差,可以判断它们是否存在显著差 异。
在生产过程中,方差用于度量产品质 量波动的程度,通过控制产品质量指 标的方差,可以提高产品质量稳定性。
03
期望与方差的关系
期望与方差的关系式
期望值是随机变量取值的平均数 ,表示随机变量的“中心趋势”
方差的性质
方差具有可加性
当两个随机变量相互独立时,它们组 合而成的随机变量的方差等于它们各 自方差的线性组合。
方差与期望值的关系
方差与期望值之间存在一定的关系, 如方差等于期望值减去偏差的平方和 再求平均值。
方差的应用
风险评估
在金融和经济学中,方差被用来度量 投资组合的风险,通过计算投资组合 中各个资产的方差和相关系数,可以 评估投资组合的整体风险。
期望与方差的拓展
期望与方差在金融中的应用
金融风险评估
利用数学期望和方差计算 金融资产的风险,评估投 资组合的风险和回报。
资产定价
利用数学期望和方差等统 计指标,对金融资产进行 定价,确定其内在价值。
保险精算
通过数学期望和方差等统 计方法,评估保险产品的 风险和回报,制定合理的 保费和赔付方案。
期望与方差在统计学中
期望与方差在其他领域的应用
在回归分析中,数学期望和方差 等统计指标用于描述因变量和自 变量之间的关系,以及预测未来
的趋势。
假设检验
在假设检验中,数学期望和方差等 统计指标用于比较两组数据或样本 的差异,判断是否具有显著性。
方差分析
方差分析利用数学期望和方差等统 计指标,分析不同组别或处理之间 的差异,确定哪些因素对数据变化 有显著影响。
质量控制
统计分析
在统计分析中,方差分析是一种常用 的统计方法,通过比较不同组数据的 方差,可以判断它们是否存在显著差 异。
在生产过程中,方差用于度量产品质 量波动的程度,通过控制产品质量指 标的方差,可以提高产品质量稳定性。
03
期望与方差的关系
期望与方差的关系式
期望值是随机变量取值的平均数 ,表示随机变量的“中心趋势”
方差的性质
方差具有可加性
当两个随机变量相互独立时,它们组 合而成的随机变量的方差等于它们各 自方差的线性组合。
方差与期望值的关系
方差与期望值之间存在一定的关系, 如方差等于期望值减去偏差的平方和 再求平均值。
方差的应用
风险评估
在金融和经济学中,方差被用来度量 投资组合的风险,通过计算投资组合 中各个资产的方差和相关系数,可以 评估投资组合的整体风险。
期望与方差的拓展
期望与方差在金融中的应用
金融风险评估
利用数学期望和方差计算 金融资产的风险,评估投 资组合的风险和回报。
资产定价
利用数学期望和方差等统 计指标,对金融资产进行 定价,确定其内在价值。
保险精算
通过数学期望和方差等统 计方法,评估保险产品的 风险和回报,制定合理的 保费和赔付方案。
期望与方差在统计学中
期望与方差在其他领域的应用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、标准差的定义
D( )
11
3、方差的常用的计算公式
(1)D(
)
E[
E(
)]2
[x
E(
)]2
p( x)dx
根据数学期望(6)E( f ( ))
f (x)p(x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
12
3、方差的常用的计算公式
1、方差的定义
D( ) E[ E( )]2
(刻画了随机变量ξ与其均值 E(的) 平均偏离程度)
2、标准差的定义
D( )
18
3、方差的常用的计算公式
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
14
下页
三、练习
• 课本第90页 第6题
15
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
(1)D( )
E[
E( )]2[x NhomakorabeaE( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
13
4、方差的性质 设 k ,b,c均为常数,则有
设连续型随机变量 的密度函数为 p(x)
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
E( ) xp(x)dx
例1 随机变量的概率密度函数
p(
x)
6x(1 x),当0 x 1
0
当x 0或x 1时
求随机变量的数学期望。
9
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
19
4、方差的性质 设 k ,b,c均为常数,则有
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
20
下页
五、作业
• 课本第90页 第5题
21
(2)方差的简便计算公式
D( )=E( 2) E(2 )
5
4、方差的性质
(1)D(c) 0
(3)D( b) D( )
(2)D(k ) k 2D( ) (4)D(k b) k 2D( )
6
二、新课
(一)连续型随机变量ξ取值的数学期望
设连续型的概率密度函数y p(x)
在x轴上取很密的分点: y
η
b0
b1
L
P p(b0 )x0 p(b1)x1
L
bn1
p(bn 1 )xn 1
n
E 与E 很接近,E = bi p(bi )xi
i 1
n
nn ,maxxi0 lim 如果 bi p(bi )xi的极限存在 n
i 1
bi p(bi )xi
xp(x)dx
E
i1
8
1、连续型随机变量的数学期望的定义
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
10
(二)连续型随机变量ξ取值的方差
1、方差的定义
D( ) E[ E( )]2
(刻画了随机变量ξ与其均值 E(的) 平均偏离程度)
k
2
2、数学期望的性质
(1)EaX b aEX b (2)EaX aEX (3)EX b EX b
(4)Eb b X b P1
(5)EX Y EX EY
(6)E f ( ) f (xk )PK 3 k
(二)离散型随机变量取值的方差 1、方差的定义
D( ) E[ E( )]2
E( ) xp(x)dx
16
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
17
(二)连续型随机变量ξ取值的方差
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
7
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
L
P p(b0 )x0 p(b1)x1
L
【xn1, xn)
p(bn 1 )xn 1
离散型随机变量η的概率分布表:
(刻画了随机变量ξ与其均值 E(的) 平均偏离程度)
2、标准差的定义 D( )
4
随 3、方差的常用的计算公式
机 变 量
x1
x2
[ E( )]2 [x1 E( )]2 [x2 E( )]2
P
p1
p2
··· xn
···[xn E( )]2
··· pn
(1)D( ) E[ E( )]2 [x1 E( )]2 P1 [x2 E( )]2 P2 [xn E( )]2 Pn
2020年4月3日星期五
1
一、复习
(一)离散型随机变量取值的数学期望
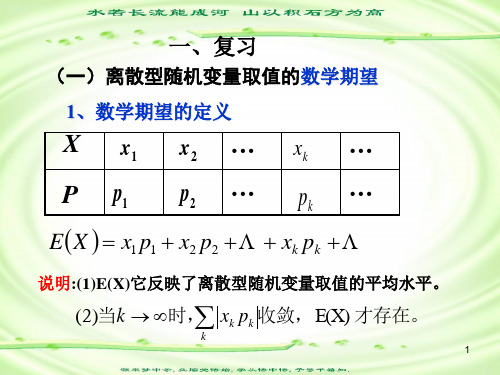
1、数学期望的定义
X x1 x2 ··· xk ···
P p1 p2 ··· pk ···
EX x1 p1 x2 p2 xk pk
说明:(1)E(X)它反映了离散型随机变量取值的平均水平。
(2)当k 时, xk pk 收敛,E(X) 才存在。
