频率特性和时域性能指标的关系
频域性能指标和时域性能指标的关系
5.7 频域性能指标和时域性能指标的关系频率响应法是通过系统的开环频率特性和闭环频率特性的一些特征量间接地表征系统的瞬(暂)态响应的性能，因而这些特征量又被称为频域性能指标。
常用的频域性能指标有幅值裕度、相位裕度、谐振峰值、谐振频率和频带宽度等。
虽然这些指标没有时域性能指标那样直观，但在二阶系统中，它们与时域性能指标有着确定的对应关系，对于高阶系统，也有近似的关系。
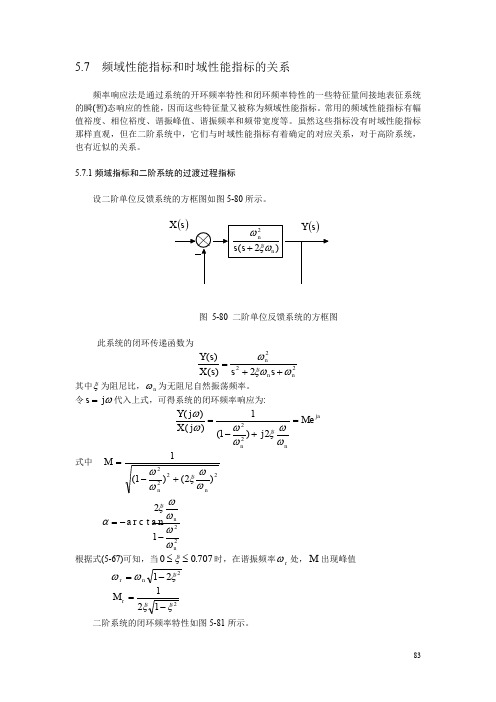
5.7.1频域指标和二阶系统的过渡过程指标设二阶单位反馈系统的方框图如图5-80所示。
图 5-80 二阶单位反馈系统的方框图此系统的闭环传递函数为2222)()(nn n s s s X s Y ωξωω++= 其中ξ为阻尼比，n ω为无阻尼自然振荡频率。
令s j =ω代入上式，可得系统的闭环频率响应为:ja n nM j j X j Y e 2)1(1)()(22=+-=ωωξωωωω式中 M nn =-+1122222()()ωωξωω2212a r c t a n nn ωωωωξα--= 根据式(5-67)可知，当00707≤≤ξ.时，在谐振频率ωr 处，M 出现峰值ωωξr n =-122M r =-1212ξξ二阶系统的闭环频率特性如图5-81所示。
图 5-81 图5-80所示系统的闭环频率特性对于二阶系统，在012≤<ξ时，频率特性的谐振峰值M r 可以反映系统的阻尼系数ξ，而其谐振频率ωr 可以反映给定ξ对应的自然频率ωn ,从而也能反映响应速度。
这样就可把二阶系统闭环频率特性的M r 和ωr 当作性能指标用。
系统的频带宽度(带宽)由图5-81可见，当ωω>r 时，闭环频率特性的幅值M 单调下降。
当闭环频率特性的幅值下降到707.021==M 时，或者说，当闭环频率特性的分贝值下降到零频率时分贝值以下3分贝时，对应的频率ωb 称为截止频率，又称带宽频率。
此时有b j M j M ωωω>-<3)0(lg 20)(lg 20对于0)0(lg 20=j M ，有b j M ωωω>-<3)(lg 20系统对频率高于ωb 的输入衰减很大，只允许频率低于ωb 的输入通过。
频率特性与系统性能的关系
得
2
第四节 频率特性与系统性能的关系
例 分析随动系统的性能，求出系统的频 域指标ωc、γ和时域指标σ%、 ts。 (1) 随动系统结构如图 20 解： G(s)= s(0.5s+1) ω L( ) dB c 20ω≈1 ω ωn = -20dB/dec 2 c =6.3 可得：0.54 c -2 2 =6.5 20 ζ +1 4ω ζ ωc 0 2 γ=180o+- π ( ζ c2) ζυ ω e 1- 100% =57% -20 σ%= o o -1 =180 -90 - tg (0.5×6.3) υ (ω ) 6 tso=ω tg o =3s o 0 γ =17.62 c =90 -72.38 -90 γ -180 ζ=γ/100=0.176
γ
判别系统稳定性 ωc 确定频率指标
主要内容 一、频率特性的基本概念 r(t)=Asin ωt ω ω)] cs(t)=A|G(j )|sin[ω t+ G(j
频率特性:
G(j ) ω
ω ω 幅频特性：A( )=|G(j )| υω ω 相频特性： ( )= G(j )
二、典型环节的频率特性 1. 奈氏图 先把特殊点找出来，然后用 平滑曲线将它们连接起来。 2. 伯德图
第四节 频率特性与系统性能的关系
二、闭环频率特性与时域指标的关系
根据开环频率特性来分析系统的性能 是控制系统分析和设计的一种主要方法， 它的特点是简便实用。但在工程实际中， 有时也需了解闭环频率特性的基本概念和 二阶系统中闭环频域指标与时域指标的关 系。
第四节 频率特性与系统性能的关系
1. 闭环频率特性及频域指标
第四节 频率特性与系统性能的关系
(2) 中频段的斜率与动态性能的关系
自动控制原理--频率特性与时域指标的关系及三频段分析法的应用
2 2
2.相位裕量： 180 (c ) arctan
2
1 4 4 2 2
5-17 5-18 5-19
Saturday, August 17当, 0< <0.6时, 100*
2024
1
3.与超调量的关系
e( / 1 2 ) p
p
4.与调整时间的关系
ts
3
n
3
2024
3
5.6.3闭环频率特性及其特征量
对于单位反馈系统其闭环传递函数为：
对应的频率特性为：
M (s) G(s) 1 G(s)
M ( j ) G( j ) M ( )e j () 1 G( j)
（5-21） （5-22）
对于非单位反馈系统，如图5-3（a）所示。
R(s)
+ -
C(s) G(s)
Saturday, August 17,
2024
15
某最小相位系统的对数幅频特性如图所示， 求 系统的开环传递函数 计算系统的相位裕量和幅值裕量 判断系统的稳定性
L（w）
-20 A
46
B 6
-40 C
W1
W2
10
100
-60
Saturday, August 17,
2024
16
解；1）低频段渐进线的斜率为-20dB，所以是1型系统（延长
当0< <0.707时, 二阶振荡环节的幅频特性曲线位于相应的渐近 线上方，系统存在峰值Mr 。对应的频率ωr为谐振频率。
r n 1 2 2
Mr
2
1
1 2 2
（5-24 ）
2.截止频率和频带宽度
自控理论 4-6频域指标与时域指标的关系
2 −40
ω
作业
4 - A -14、 4 -B - 4 、
K s(Ts + 1)
c(t)
例：已知最小相位系统的开环对数幅频特 性曲线，试求： 性曲线，试求：
L(ω)
(1) 开环传递函数 开环传递函数G(s)； ； (2) 剪切频率 ωc ； (3) 相角裕量 γ(ωc)； (4) r(t)=(1/4)t2 时的 ess 。
6 0
−40 −20 0.5
ωc
令 G ( jω c ) = 1,
解得
ω c = ω n − 2ζ 2 + 4ζ 4 + 1
γ = 180 + ϕ (ω c ) = tg
0 −1
(4 − 30)
(4 − 31)
求γ
2ζω n
ωc
将式(4-30)代入式 代入式(4-31)得 将式 代入式 得
求γ
γ = 180 + ϕ (ω c ) = tg
2.
r(t)
25 s( s + 6)
c(t)
ωn2 =25 得 ζ =0.6 ωn=5
2ζ = 59.2 0
γ = tg
−1
− 2ζ 2 + 4ζ 4 + 1
ω c = ω n − 2ζ 2 + 4ζ 4 + 1 = 3.58
3.
Mr =
1 2ζ 1 − ζ
2
= 1.04
ω r = ω n 1 − 2ζ 2 = 2.65
结论
8 t sω c = tgγ
(4 − 36)
( 2) ω c与ζ、ω n 都有关,当ζ 一定，ω c ↑→ ω n ↑→ t s ↓ 一定，
1. 简述频域和时域的关系
1. 简述频域和时域的关系
频域和时域是信号处理中两个非常重要的概念。
时域描述信号的时间特性，而频域描述信号的频率特性。
频域和时域之间有密切的关系，通过一定的变换可以将时域信号转换到频域，或将频域信号转换为时域信号。
时域信号是指信号在时间域上的变化。
它可以用函数表示，在时域上，函数的取值代表信号随时间变化时的幅度和相位。
时域序列具有很高的信息密度，可以用于对时间和相位的细微变化进行分析。
频域信号是指信号在频域上的变化。
在频域上，信号可以表示为复数形式的幅度和相位。
频域信号的频率分量可以通过傅里叶变换转换为时域信号。
频域序列可以在不同的频率范围内分析各种性质。
例如，谐波分析可以通过傅里叶变换来识别频域信号中存在的特定频率成分。
时域和频域之间的关系可以通过快速傅里叶变换（FFT）来描述。
FFT可以将时域信号转换为频域信号，并根据相同的时间域样本大小从频域中抽取频率分量。
转换后，在频域的每个频率值上都有一个振幅和相位。
类似地，通过逆傅里叶变换（IFFT），可以将频域信号转换回时域。
在实际的应用中，频域和时域经常被同时使用。
进行频域分析可以帮助确定系统的频率响应、传递函数以及其他系统特性。
时域分析通常用于调节系统，例如调整增益、滤波器参数等等。
因此，了解频域和时域的关系非常重要，可以帮助我们更深入的理解信号处理技术的原理以及它们的应用。
第5章 控制系统的频域分析法 1(48)
频率特性如图5-3所示。 由图可看出，积分环节的相 频特性等于-900 ，与角频率 ω无关.
图5-3 积分环节的频率响应
14
表明积分环节对正弦输入信号有900的滞后作用； 其幅频特性等于1/ω，是ω的函数，当ω由零变到无穷大 时，输出幅值则由无穷大衰减至零。 在[G(jω)]平面上，积分环节的频率特性与负虚轴重合。
17
1
推广：当惯性环节传递函数的分子是常数K时， 即G(jω)=k/(jTω+1)时，其频率特性是圆心 为:[k/2,0]，半径为k/2的实轴下方半个圆周。
(四）振荡环节
振荡环节的传递函数是:
(5-34)
其频率特性是:
(5-35)
图5-4 惯性环节的频率响应
幅频特性和相频特性分别为:
18
振荡环节的幅频特性和相频特性均与阻尼比ξ有关， 不同阻尼比的频率特性曲线如图所示。 当阻尼比较小时，会产生谐振，谐振峰值Mr(Mr>1) 和谐振频率ωr由幅频特性的极值方程解出。
时，输出幅值衰减很快。
当阻尼比 时，此时振 荡环节可等效成两个不同时间 常数的惯性环节的串联，即:
T1,T2为一大一小两个不 同的时间常数，小时间常数对 应的负实极点离虚轴较远，对 瞬态响应的影响较小。
图5-6 振荡环节的频率响应
21
振荡环节为相位滞后环节，最大滞后相角是180 。 推广：当振荡环节传递函数的分子是常数K时， 即 ，其对应频率特性 的起点为
G( j ) G( j ) e jG ( j ) (5 - 15)
；
称为系统的频率特性，它反映了在正弦输入信号作用 下，系统的稳态响应与输入正弦信号的关系。
9
G ( j ) G ( j ) e jG ( j )
频域响应和时域响应之间的关系_OK
8
b n (1 2 2 ) （ 5-1252）4 2 4 4
将式（5－152）等号两边分别乘以式（5－148）和式（5－149）两边得到
和
(1 2 2 ) （25-1543）2 4 4
btp
1 2
bts
1
(1 2 2 )
2（ 54－ 21544） 4 ln
1
0.05 1 2
式（5-153） 和式（5-154）说明，对于给定的阻尼比 ，二阶系统的截止频
（3）谐振频率 和r截止频率 的大b 小反映了系统的响应速度。 与 的r 值愈b
大，系统响应速度愈快，反之愈慢。但频带太宽（ 的值大）b ，系统对高频
噪声的滤波性能差，因此在系统设计中，必须兼顾系统的快速性和抗干扰能
力，妥善处理好这一对矛盾。
返回13
5.8 MATLAB在频域分析中的运用
5.8.1 用MATLAB绘制频率响应图
C(t) 1 C ( j ) R( j ) e jt d
2 R( j )
（5-159）
式中 C为(t)系统的被控信号，
C( j分) 和别R是( j系)统的闭环频率特性和 R( j)
控制信号的频率特性。一般情况下，直接应用式（5—159）求解高阶系统的
时域响应是很困难的。在第三章和第四章我们介绍了主导极点的概念，对于
§ 5-7 频域响应和时域响应之间的关系
频域响应（频率特性）和时域响应都是描述控制系统固有特性的工具， 因此两者之间必然 存在着某种内在联系，这种联系通常体现在控制系 统频率特性的某些特征量与时域性能指标之间的关系上。本节将着重讨 论系统闭环幅频特性的特征量与系统性能指标之间的关系。 典型闭环 幅频特性如图5—70所示，特性曲线随着频率变化的特征可用下述一些 特征量加以概括：
自动控制原理-频率特性与系统性能的关系课件
第四节 频率特性与系统性能的关 系
（2） ωc、γ与ts 之间的关系
根据：
ts=
3 ζωn
ts·ωc=3
4ζ4+1 -2ζ2 ζ
整理得
ts·ωc=
6 tgγ
调节时间 ts 与ωc以及γ有关。γ不变 时，穿越频率ωc 越大，调节时间越短。
第四节 频率特性与系统性能的关 系
例 采用频率法分析随动系统的性能，求 出系统的频域指标ωc、γ和时域指标 σ%、 ts。
系
闭环幅频特性曲线
系统的闭环频率 指标主要有：
1 零频幅值Mo
M(ω)
Mm
M0
0.707M(0)
432ω幅M程M=频o度0=o谐的带=谐谐最1闭上M时振幅闭宽振振大环反(，峰ω频环频频峰值峰映)输值=值幅率率值与了值M出反降值ωMωM零系出(与0映br到γr频)=统现输了0幅的时M.M7入系0值Mm快的o7相统(M之0速频ω等的0比b性率时)，相=。。。的ω0没对.r在7频有稳0ω一率7误b定M定。差性0 的。ω
第四节 频率特性与系统性能的关 系
低频段的对数频率特性为：
L(ω)=20lgA(ω)=20lg
K ωv
=20lgK-v·20lgω
对数幅频特性曲线
对数幅频特性曲
L(ω)/dB
线的位置越高，开
ν=0 ν=1 -20ν ν=2 0 νK K
环增益K 越大，斜
率越负，积分环节
K
ω 数越多。系统稳态 性能越好。
1)=τ9=00o-.0712.38o+3.6o
L(ω)/dB
系统=2开1.环22传o 递函数 ξ=γ/100=0.21
ωGn=(s)=4ζ2S04(ω(+001c..05-12SζS+2+1=1)6).59
第四章 频域分析(第四-六节)
－20 －20
/(rad s 1 )
K
－40
/(rad s 1 )
K
b)
－40
a)
(3) Ⅱ 型 系 统 n = 2 ， 其 低 频 段 是 斜 率 为 - 4 0 d B / d e c 的 直 线 ， 该 直 线 或 其 延 长 线 与 0 d B 线 ( 横 轴 )的 交 点 频 率 为 w a , 此 时 ， K = w a。
p
= e
- xp /
1- x
2
和谐振峰值M
r
= 1 / 2x 1- x
2
可 以 看 出 ， 它 们 均 随 着 阻 尼 比 x的 增 大 而 减 小 。 由 此 可 见 ， M r 越 大 的 系 统 ， 相 应 的 M p也 越 大 ， 瞬 态 响 应 的相对稳定性越差。为了减弱系统的振荡性，同时使 系 统 又 具 有 一 定 的 快 速 性 ， 应 当 适 当 选 取 M r值 。 如 果 M r 取 值 在 1＜ M r ＜ 1 .4 范 围 内 ， 相 当 于 阻 尼 比 x 在 0 .4 ＜ x ＜ 0 .7 范 围 内 ， 这 时 二 阶 系 统 阶 跃 响 应 的 超 调 量 M p ＜ 25% 。
= e
由 此 可 见 ， 最 大 超 调 量 M p和 谐 振 峰 值 M r都 随 着 阻 尼 比 x的 增 大 而 减 小 。 同 时 随 着 M r的 增 加 ， 相 应 地 M p也 增 加 ， 其 物 理 意 义 在 于 ： 当 闭 环 幅 频 特 性 有 谐 振 峰 值 时 ， 系 统 的 输 入 信 号 的 频 谱 在 w = w r附 近的谐波分量通过系统后显著增强，从而引起振 荡。
开环对数频率特性和时域指标.
5-6 开环对数频率特性和时域指标根据系统开环对数频率特性对系统性能的不同影响，将系统开环对数频率特性分为三个频段。
即低频段、中频段和高频段。
一、 低频段低频段通常是指开环对数幅频特性的渐近曲线在第一个交接频率以前的频段，这一频段完全由开环传递函数中的积分环节和放大环节所决定。
低频段的对数幅频为ωωωωlg 20lg 20lg 20)()(lg 20⨯-==v K Kj H j G v (5-32)式中v 为开环传递函数中的积分环节数。
根据式(5-32)及积分环节数，就可作出开环对数幅频特性曲线的低频段，如图5-39所示。
若已知低频段的开环对数幅频特性曲线，则很容易得到K 值和积分环节数v ，故低频段的频率特性决定了系统的稳态性能。
二、中频段中频段是指开环对数幅频特性曲线截止频率c ω附近的频段。
这决定系统的稳定程度，即决定系统的动态性能。
设有二个系统，均为最小相位系统，它们的开环对数幅频特性曲线除中频段的斜率不同(即一个为20-dB/dec,另一个为40-dB/dec) 之外， 其余低频、 高频段均相同。
并且中频段相当长，如图5-40 所示。
显然，系统(a)有将近90°的相裕量，而系统(b)则相裕量很小。
假定另有二个系统， 均为最小相位系统， 开环对数幅频特性曲线除中频段 (斜率为 -20 dB/dec ) 线段的长度不同外， 其余部分完全相同， 如图 5-41 所示。
显然， 中频段线段较长的系统 (a) 的相裕量将大于中频段线短的系统(b)。
可见，开环对数幅频特性中频段斜率最好为20-dB/dec ，而且希望其长度尽可能长些，以确保系统有足够的相角裕量。
如果中频段的斜率为40-dB/dec 时，中频段占据的频率范围不宜过长，否则相裕量会很小；若中频段斜率更小(如60-dB/dec)，系统就难以稳定。
另外，截止频率c ω越高，系统复现信号能力越强，系统快速性也就越好。
三、 高频段高频段是指开环对数幅频特性曲线在中频段以后的频段(一般c ωω10>的频段)。
控制工程(自动控制)第十八课 频率特性与时域指标
闭环频率特性主要性能指标
带宽频率ω 带宽频率ωb:当闭环幅频特性下降到频率为零时的分 贝值以下3分贝时,对应的频率称为带宽频率ω 贝值以下3分贝时,对应的频率称为带宽频率ωb . 频率范围(0,ωb)称为系统的带宽. 频率范围( 称为系统的带宽.
ω > ωb
20 lg Φ ( jω ) < 20 lg Φ ( j 0) 3
πζ / 1ζ 2
ζ =
1 1 1 2 Mr 2
π
2 M r M r 1 2 M r + M r 1
σ% = e
× 100%
ts =
3.5
ζωn
( = 0.05, 0 < ζ < 0.9)
因此,若知道频域指标中的任两个, 因此,若知道频域指标中的任两个,就可解算 从而求出时域指标.反之, 出ζ和ωn,从而求出时域指标.反之,给出时域指 标的任两个,就可确定闭环频域指标. 标的任两个,就可确定闭环频域指标.
高阶系统
1 Mr = ( 35 ° ≤ γ ≤ 90 ° ) sin γ σ = 0 . 16 + 0 . 4 ( M r 1) (1 ≤ M ts = kπ ≤ 1 .8 )
r
ωc
(1 ≤ M
r
k = 2 + 1 . 5 ( M r 1) + 2 . 5 ( M r 1) 2
≤ 1 .8 )
2 b 2 2 n
1 = 20 lg 2
ω jα ( ω ) Φ ( jw) = = M (ω )e 2 2 ( jω ) + 2ζω n ( jω ) + ωn
2 n
M (ω ) =
1
ωb2 2 ωb 2 [1 2 ] + [2ζ ] ωn ωn
自动控制原理5第七节闭环系统性能分析
利用频率特性分析系统的性能： 稳定性、稳态性能、瞬态性能
1
⒈ 频率尺度与时间尺度的反比关系
若有两个系统的频率特性F1(jw)和F2(jw)有如下关系
F1
(
jw
)
F
2
(
j
w
)
0
则两个系统的阶跃响应有如下关系
h1(t) h2 (t) 这个性质说明频率特性展宽多少倍，输出响应将加快多少倍。
-140
-160
10
100-18w0
3
⒉ 频率特性与系统性能的关系 ① 频率响应的低频区(远低于幅值穿越频率的区域)，表征了
闭环系统的稳态特性；
② 频率响应的高频区(远高于幅值穿越频率的区域)，表征了 闭环系统输出响应的起始部分；
③ 频率响应的中频区(靠近幅值穿越频率的区域)，表征了闭
环系统的稳定性和瞬态性能。
L(w) 20lg K 20lg 1 (0.2w)2 20lg 1 (0.05w)2 60lg w 20lg 1 (0.01w)2 20lg 1 (0.002w)2
(w ) tg10.2w tg10.05w 270 tg10.01w tg10.002w
18
100 80 60 40 20 0 -20 -40 -60 -80
L1 (1)
当w 1时，有：L1(1) 20 log k ，故：k 10 20
L(w)(dB) 20lgK -20
w -40
L(w)(dB) -20
-40
20lgK
-20
w
1 -40
L(w)(dB)
-40
-20 1
w
20lgK
-40
(a) 0型系统
控制系统时域及频域性能指标的联系
控制系统时域与频域性能指标的联系经典控制理论中,系统分析与校正方法一般有时域法、复域法、频域法.时域响应法是一种直接法，它以传递函数为系统的数学模型,以拉氏变换为数学工具，直接可以求出变量的解析解.这种方法虽然直观，分析时域性能十分有用，但是方法的应用需要两个前提,一是必须已知控制系统的闭环传递函数,另外系统的阶次不能很高。
如果系统的开环传递函数未知，或者系统的阶次较高,就需采用频域分析法。
频域分析法不仅是一种通过开环传递函数研究系统闭环传递函数性能的分析方法,而且当系统的数学模型未知时，还可以通过实验的方法建立。
此外，大量丰富的图形方法使得频域分析法分析高阶系统时，分析的复杂性并不随阶次的增加而显著增加。
在进行控制系统分析时，可以根据实际情况，针对不同数学模型选用最简洁、最合适的方法,从而使用相应的分析方法，达到预期的实验目的.系统的时域性能指标与频域性能指标有着很大的关系，研究其内在联系在工程中有着很大的意义.一、系统的时域性能指标延迟时间t d阶跃响应第一次达到终值h （∞）的50％所需的时间上升时间t r阶跃响应从终值的10%上升到终值的90%所需的时间;对有振荡的系统，也可定义为从0到第一次达到终值所需的时间峰值时间tp阶跃响应越过终值h （∞)达到第一个峰值所需的时间调节时间ts阶跃响应到达并保持在终值h （∞)的±5％误差带内所需的最短时间超调量%σ 峰值h(tp）超出终值h(∞）的百分比，即%σ=()()()∞∞-h h h t p ⨯100%二、系统频率特性的性能指标采用频域方法进行线性控制系统设计时,时域内采用的诸如超调量,调整时间等描述系统性能的指标不能直接使用，需要在频域内定义频域性能指标。
1、零频振幅比M （0)：即ω为0时闭环幅频特性值。
它反映了系统 的稳态精度， M(0）越接近于1，系统的精度越高.M(0）≠1时，表明系统有稳态误差。
2、谐振峰值Mr ：为幅频特性曲线的A （ω）的最大值.一般说来，Mr 的大小表明闭环控制系统相对稳定性的好坏。
频率特性与时域响应的关系
0 < ξ ≤ 0.707
2
σ % = e
ξ
σ%
Mr
1弦输
入信号响应的平稳性
（2） γ 与 σ% 的关系
G( jω)H( jω) =
ωn ( jω)[( jω) + 2ζωn )
2
| G( jωc )H( jωc ) |=1
ωc = ωn
4ξ 2 +1 − 2ξ 2
（二）闭环频率特性性能指标 （1）零频振幅比 M(0) （2）相对谐振峰值 Mr （3）谐振频率 ωr （4）闭环频带宽度 ωb
M (dB)
M
r
M0
0.707 M 0
0
ωr
ωb
ω
二、频率域特性指标与时域瞬态指标的关系 1、频域描述与时域描述的反比性质 设两系统的关系为：
G2 (s) = G1 (αs)
ν
20lg k
ω0
1
四、系统Bode图中频段、高频段分析 （1）中频段： Bode图中幅频特性曲线 在截止频率 ωc 附近的区段。可粗略认 为0dB线上下15dB范围内的频率段。
10 G(S) = S(0.5S +1)
100(0.2S +1) G(S) = 2 S (0.02S +1)
L(ω)
10 G(S) = S(0.5S +1)
ωn2
(ωn −ω2 )2 + (2ζωnω)2
2
ωb = ωn 1− 2ζ + 2 − 4ζ + 4ζ
ts = 3
4
ξωn
ωbts =
3
ξ
1− 2ζ + 2 − 4ζ + 4ζ
2 2
开环频率特性与系统时域指标的关系
L (w ) d B
120
80 -20
40
20
0.01 0.085 0.1 1.7
1
40 60
12 40
w 60
11
结论 由前面对二阶系统和高阶系统的分析可知，
系统开环频率特性中频段的两个重要参数 、
Ⅱ型系统
-40
数增加），都有利于
系统稳态误差的减小。
-20
0
w =1
w1
w = Ka
5
5.6.2 中频段
极坐标图
伯德图
(-1,j0)点 A(w)=1时,曲线上的频率点
0db线和-180相角线 截至频率wc
中频段就是指L(w)穿过0dB线(即wc附近)的频段，其斜率及宽度 (中频段长度)集中反映了动态响应中的平稳性和快速性。
5.6 开环频率特性与系统时域指 标的关系
1
5.6.1 低频段
系统型号
0 I II
误差系数 Kp Kv Ka
K0 0 K0
K
单位阶跃 单位速度
输入
输入
r(t) = R ·1(t) r (t ) = Rt
R 1+ Kp
R
0
Kv
0
0
1. 稳态误差与输入、系统结构有关. 2. 减小或消除稳态误差的方法：
二阶系统
G(s) = K =
wn2
R(s) +
w n2
C (s)
s(Ts +1) s(s + 2wn )
s(s + 2w n )
自动控制原理 第二十一章 频率特性和时域性能指标的关系
Ts 1
L( )
3dB
c
1 T
b log
频域性能指标：
由频b 宽的c 定T1义知：A(我b们) 知1道2 一A(0阶) 惯 0性.70环7 ,节20的log调A整(时bt)s间是33Td：(B, 5)
则频宽越大，调整时间越小。
二阶系统：
开环频率特性为：Gk ( j
第七节 频率特性和时域性能指标的 关系
主要内容
通过频率特性曲线获得稳态性能指标 频率域性能指标 频率域特性指标与时域瞬态指标的关系
一、稳态性能指标分析：
如果通过频率特性曲线能确定系统的无差度阶数 （即积分
环节的个数）和开环放大系数k的话，则可求得系统的稳态误差。 （见第三章第六节 稳态误差分析）
数定义为幅值稳定裕度。所对应的频率 称为相角穿越频率。
即
L
hA2(01 lgg)，A(满 足)。
(
) 180 。实际中常用对数幅值稳定裕度
相角稳定裕度 系统开环频率特性的幅值为1时，系统开环频率特性的相角
与180 之和定义为相角稳定裕度，所对应的频率 称为系统截 止频率或幅值穿越频率。即 180 ( ) ， 满足 A( ) 1
闭环频率特性为：( j)
)
(
n2
(
j)((
j ) 2
n2
2
n
(
j)2 2 n ( j) n
j ))
2 A(
)e
j
(
)
频域性能指标主要有相位稳定裕度（开环指标）和频宽、谐振
峰值（闭环指标）。
幅频特性为：A()
n2
(n2 2 )2 (2 n )2
由带宽的定义知当 A()
1 A(0) 2
自动控制原理7第七节频率特性和时域性能指标的关系
案例剖析：某型导弹控制系统设计优化
1. 调整控制器参数，改善系统频率特性。
2. 引入先进的控制算法，如自适应控制、鲁棒控 制等。
3. 对执行器和传感器进行改进，提高系统动态性 能。
优化效果：经过优化后，导弹控制系统的稳定性 和快速性得到了显著提高，超调量和稳态误差明 显减小。在实际飞行试验中，导弹的命中精度得 到了有效提升。
02 4. 对实验数据进行处理和分析，提取时域性能指 标。
03 5. 对比不同频率特性下的时域性能指标，分析它 们之间的关系。
数据采集、处理及结果展示
数据采集
使用高精度传感器采集系统响应数据，包括输出信号、误差信号等。
数据处理
对采集到的数据进行滤波、去噪等预处理操作，以提高数据质量。 然后，计算时域性能指标，如超调量、调节时间、稳态误差等。
05
实验验证与案例分析
实验设计思路及步骤介绍
实验设计思路及步骤介绍
01
步执行器、传感器等硬件设备 ，以及相应的软件系统。
03
2. 设计不同频率特性的控制器，如低通、高通、带通等，并 分别进行实验。
实验设计思路及步骤介绍
01 3. 对每个实验，施加相同的输入信号，并记录系 统响应数据。
高频段增益越大，系统的稳态误差越小。
稳态误差与带宽的关系
带宽越宽，系统的稳态误差越小。
04
典型系统频率特性和时域 性能指标关系探讨
一阶系统
频率特性
一阶系统的频率响应是单调的，没有谐振峰。其幅频特性随频率的增加而单调下降，相频特性则随频 率的增加而线性增加。
时域性能指标
一阶系统的主要时域指标包括上升时间、峰值时间和调节时间。这些指标与系统的阻尼比和自然频率 有关，阻尼比越小，上升时间和峰值时间越短，调节时间越长；自然频率越高，系统的响应速度越快 。
新编文档-开环频率特性与系统时域指标的关系-精品文档
闭环系统的动态性能主要取决于开环对数幅 频特性的中频段。
12
5.7 闭环频率特性分析
13
1.闭环频率特性指标与时域响应的关系
闭环频域指标：
M (dB)
（1）零频幅值M0： w=0时闭环幅值。
Mr
(jw)=C R((jjw w))=M(jw)ej(w)
3
（1）p%与Mr的关系
Mr
谐振频率为：ω r=ω n 12ζ2 (0ζ0.707) 2
Mr
谐振峰值：
Mr = 2ζ
1 1ζ2
(0ζ0.707)
1
p
p
可见，Mr与成反比。相同的，Mr较高，
超调量p也大，且收敛慢，平稳性及快速 0
0.2 0.4
0.6 0.8 1.0
性都差。当Mr=1.21.5时，对应p =20
（2）谐振峰值Mr： 闭环幅频最大值。
M0
（3）谐振频率wr： 0.707 M 0
谐振峰值时频率。
（4）频带宽度wb：
0
wr
wb
w
闭环幅值减小到0.707 M0时的频率。0wwb，称为频带宽度。
通常用Mr和wb（或wr）作为闭环系统的频域动态指标。Mr过 大会使系统振荡剧烈、平稳性差，而频带宽度wb大则系统响应较 快。
高频段指L(w)曲线在中频段以后的区段，反映出系统 的低通滤波特性，形成了系统对高频干扰信号的抑制能力。
L (w ) d B
120
80 -20
40
20
0.01 0.085 0.1 1.7
1
40 60
12 40
w 60
11
控制系统的时域与频域特性分析
将时域信号转换为频域信号，通过分析频谱特性来了解信号的频率组成和变化规 律。
频域分析
通过分析系统的频率响应，了解系统在不同频率下的性能表现，有助于揭示系统 的内在特性。
控制系统设计中的时频转换
时频转换
在控制系统设计中，时频转换是一种 重要的技术手段，用于将时域特性与 频域特性相互转换，以便更好地进行 系统分析和设计。
VS
详细描述
时频联合分析结合了时域和频域分析的方 法，通过同时考虑系统的时域和频域特性 ，全面了解系统的动态特性和稳定性。例 如，对于一个控制系统，可以通过时频联 合分析计算系统的时频响应曲线，从而更 全面地评估系统的性能和稳定性。
06 结论
控制系统的时域与频域特性总结
稳定性
通过分析系统的极点和零点，可以判断系统 的稳定性。极点位于复平面的左半部分时， 系统不稳定；而零点同样影响稳定性，需要 综合考虑。
稳定性
系统在受到扰动后恢复平衡状态 的能力，分为稳定、临界稳定和 不稳定三种状态。
阶跃响应与冲激响应
阶跃响应
系统在阶跃输入信号下的动态行为， 反映系统的动态性能和调节能力。
冲激响应
系统在冲激输入信号下的动态行为， 用于评估系统的暂态性能和稳态误差 。
时域性能指标
上升时间
系统输出从稳态值的 10%上升到90%所需的
快速性
系统的快速性主要通过调节时间常数实现， 时间常数小的系统响应速度快。
控制系统的时域与频域特性总结
• 准确性：系统的准确性由最大误差决定，可通过优化系统 参数减小误差。
控制系统的时域与频域特性总结
带宽
带宽反映了系统对不同频率信号的响应能力，带 宽越大，系统对高频信号的响应越好。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
则频宽越大，调整时间越小。
T
二阶系统：
Gk ( j ) 开环频率特性为：
( j )(( j ) 2 2 n ( j )) n 2 j ( ) 闭环频率特性为： ( j ) A ( ) e 2 ( j ) 2 2 n ( j ) n
2018年11月4日星期 日 7
2018年11月4日星期 日
6
三、典型一阶系统和二阶系统的频率特性与瞬态性能指标的关系 一阶系统：
传递函数为： (s)
频域性能指标：
1 Ts 1
L( )
3dB
c
1 T
b log
1 A(0) 0.707,20 log A( b ) 3dB, 由频宽的定义知：A( b ) 2 1 ts 3T ( 5) 我们知道一阶惯性环节的调整时间是： b c
若将带宽定义在波德图上，则当 A( b )
20log A( b ) 20log
时，有：
图示如右：
1 3.01dB 2
3.01dB
c b
2018年11月4日星期 日
8
带宽的物理意义：因为 | Y ( j ) || X ( j ) | ，随着 , | A( j ) |,当 | A( j ) | 1 时，表示
在波德图上，低频渐进线的斜率 和 的关系如下： 由 20 (dB / Dec) ，可求得 值；也可由 ( ) | 0 ， 求 。
2
开环放大系数k的求法有两种： ①低频渐进线为： L1 ( ) 20 log |
k
( j ) L1 (1) L1 (1) 20log k ，故： 当 1 时，有： k 10 20
2018年11月4日星期 日
4
二、频域性能指标 （一）、开环频率特性性能指标 幅值稳定裕度 系统开环相频特性为 180时，系统开环频率特性幅值的倒 称为相角穿越频率。 数定义为幅值稳定裕度。所对应的频率 1 即 h A( g ) ，满足 ( ) 180。实际中常用对数幅值稳定裕度 L 20 lg A( )。 相角稳定裕度 系统开环频率特性的幅值为1时，系统开环频率特性的相角 与180 之和定义为相角稳定裕度，所对应的频率 称为系统截 满足 A( ) 1 止频率或幅值穿越频率。即 180 ( ) ，
时， p
1 2
0 。当
1 2
时，无谐振峰值。当 值。 时，有谐振峰
1 2 1 2
10
M p A( p )
2018年11月4日星期 日
小结
2018年11月4日星期 日
11
| A( j ) ||
Y ( j ) |，当 | A( j ) | 1 时，表示 X ( j )
出衰减了0.707倍或-3分贝。 再增加，输出衰减得更厉害，这时 对实际系统来说，已不能正常使用了。 在实际应用中，一般用 c （或略大一些）来估计 b。显 然这种估计是偏于保守的。
2 1 | Y ( j ) | | X ( j ) | 0.707 | X ( j ) |, 即20 log | A( j ) | 3.01dB ，输 2
2018年11月4日星期 日
5
（二）、闭环频率特性性能指标
常用的有下列两项： 谐振峰值M P ：系统闭环频率特性幅值的最大值。 系统带宽和带宽频率： 设 M j 为系统的闭环频率特性， 当幅频特性 M j 下降到 2 M 0 时，对应的频率 b 称为带宽 频率。频率范围 [0, b ]2 称为系统带宽。
第七节 频率特性和时域性能指标的 关系
2018年11月4日星期 日
1
主要内容
通过频率特性曲线获得稳态性能指标 频率域性能指标 频率域特性指标与时域瞬态指标的关系
201指标分析： 如果通过频率特性曲线能确定系统的无差度阶数 （即积分 环节的个数）和开环放大系数k的话，则可求得系统的稳态误差。 （见第三章第六节 稳态误差分析）
2018年11月4日星期 日
9
谐振频率，谐振峰值
幅值 A( )与 的关系： n
对A( ) 求导并令等于零， 可解得 A( ) 的极值 p 。
p n 1 2 2
0.1
A( )
0.2 0.5
0.707
n
称为谐振峰值频率。 1 可见，当 2 0.707
n 2
频域性能指标主要有相位稳定裕度（开环指标）和频宽、谐振 峰值（闭环指标）。 n2 A( ) 幅频特性为： 2 2 2 2
( n ) (2 n )
1 1 A(0) 2 2
由带宽的定义知当 A( )
时的频率b 为带宽频率。得：
1 2
b n 1 2 2 2 4 2 4 4
20log k L1 (1)
2018年11月4日星期 日
| 20 log k 20 log
低频渐进线斜率=-20v
L1 ( )
1
3
②当 1时，k也可由L1 ( ) 与横轴的交点0 来求。
L(0 ) 0 ，有： 当 0时，
20log k
0
1
0 20logk 20 log0 ,k 0