黑龙江省哈尔滨第六中学2014-2015学年高二上学期期末考试数学(理)试题
黑龙江省哈尔滨市第六中学2015届高三10月月考数学(文)试题

黑龙江省哈尔滨市第六中学2015届高三10月月考数学(文)试题考试时间:120分钟 满分:150分 一、选择题:(每题5分,共60分) 1.已知βα,R∈,则“βα=”是“βαtan tan =”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 2.下列有关命题的说法正确的是( )A.命题“若21,x =则1x =”的否命题为“若21x =则1x ≠”B .“1x =-”是 “2560x x --=”的必要不充分条件 C. 命题若“x y =”则“sin sin x y =”的逆否命题为真D .命题“2000,10x R x x ∃∈++<”的否定是“对01,2>++∈∀x x R x 。
” 3.已知α为第二象限角,53s i n=α,则si n α=( ) A .2524-B.2512- C.2512 D.2524 4.17cos 30cos 17sin -47sin ( ) A.23-B.21-C.21D.235.已知点)1,1(-A 、)2,1(B 、)1,2(--C 、)4,3(D ,则向量→-AB 在→-CD 方向上的投影为 ( )A .223 B .2153 C .223-D .2153-6.已知向量),2,2(),1,1(+=+=→→λλn m 若)()(→→→→-⊥+n m n m ,则=λ( )A .4-B .3-C .2-D .1-7.函数sin()y A x ωϕ=+的部分图像如图所示, 则其解析式可以是( )A .3sin(2)3y x π=+B .3sin(2)3y x π=-+ C .13sin()212y x π=+D .13sin()212y x π=-+8.要得到函数)12cos(+=x y 的图象,只要将函数x y 2cos =的图象( ) A . 向左平移1个单位 B. 向右平移1个单位 C. 向左平移 12个单位 D. 向右平移12个单位9.已知函数f (x )是定义在[]12a ,a -上的偶函数,且当0x >时, f (x )单调递增,则关于x的不等式1f (x )f (a )->的解集为( )A .45[,)33B .2112,,3333⎛⎤⎡⎫-- ⎪⎥⎢⎝⎦⎣⎭ C .1245,,3333⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦D .随a 的值而变化10.已知定义在R 上的奇函数)(x f 满足)()2(x f e x f -=+(其中 7182.2=e ),且在区间[]e e 2,上是减函数,令21=a ,51,31==c b ,则( ) A .)()()(c f b f a f << B .)()()(a f c f b f << C .)()()(b f a f c f <<D .)()()(a f b f c f <<11. 在△ABC 中,角A 、B 、C 所对的边分别是c b a ,,且BC 边上的高为2a ,则cbb c +的最大值为 ( )A .22 B2 C 2 D 412.已知函数0x a e ,x f (x )ln x,x ⎧⋅≤=⎨->⎩,其中e 为自然对数的底数,若关于x 的方程0f (f (x ))=,有且只有一个实数解,则实数a 的取值范围为( )A. ()0,-∞B. ()()001,,-∞C. ()01,D. ()()011,,+∞二、填空题(每题5分,共20分) 13.函数()f x =____________。
哈尔滨市第六中学2021-2022年度高一下学期期末考试数学试卷含答案

试卷第1页,共6页哈尔滨市第六中学2021级高一下学期期末考试数学试题一、单选题(本题共8个小题,每小题5分,共40分.在每小题所给出的四个选项中,只有一项是符合题目要求的.)1.设()21i 2z -=,则z =()A.2BC .1D .22.某校有男生3000人,女生2000人,学校将通过分层随机抽样的方法抽取100人的身高数据,若按男女比例进行分层随机抽样,抽取到的学生平均身高为165cm ,其中被抽取的男生平均身高为172cm ,则被抽取的女生平均身高为()A .154.5cm B .158cm C .160.5cm D .159cm 3.如图,四面体ABCD中,BD =,2AC =,M 、N 分别为BC 、AD 的中点,1MN =,则异面直线AC 与BD )A .3πB .2πC .6πD .4π4.对于数据:2、6、8、3、3、4、6、8,四位同学得出了下列结论:甲:平均数为5;乙:没有众数;丙:中位数是3;丁:75百分位数是7,正确的个数为()A .1B .2C .3D .45.如图,正四棱柱1111ABCD A B C D -中,O 是底面ABCD 中心,,E F 分别是11,BB DD 的中点,则下列结论正确的是()A .1AO //EFB .1A O EF ⊥C .1AO //平面1EFB D .1A O ⊥平面1EFB 6.甲、乙两名同学均打算高中毕业后去A ,B ,C 三个景区中的一个景区旅游,甲、乙到A ,B ,C 三个景区旅游的概率分别如表,则甲、乙去不同景区旅游的概率为()去A 景区旅游去B 景区旅游去C 景区旅游甲0.40.2乙0.30.6A .0.66B .0.58C .0.54D .0.52试卷第2页,共6页7.四棱锥P ABCD -的外接球O 的半径为2,PA ⊥平面ABCD ,底面ABCD 为矩形,2AB =,则平面PAD 截球O 所得的截面面积为()A .4πB .3πC .2πD .π8.如图,四棱锥P ABCD -的底面ABCD 为直角梯形,1PA AB BC ===,90ABC ∠= ,120PAB ∠= ,AB //DC ,2DC PC ==,则点P 到平面ABCD 的距离为()ABC .2D .13二、多选题(本题共4个小题,每小题5分,共20分.在每小题所给出的四个选项中,有多个选项符合题目要求,全部选对得5分,漏选得2分,错选得0分.)9.新中国成立以来,我国共进行了7次人口普查,这7次人口普查的城乡人口数据如图所示.根据该图数据判断,下列选项中正确的是()A .乡村人口数均高于城镇人口数B .城镇人口比重的极差是50.63%C .城镇人口数达到最高峰是第7次D .和前一次相比,城镇人口比重增量最大的是第6次10.已知复数1z ,2z 满足1225i z z +=-,1223i z z -=,则()A.1z B .22i z =+C .123iz z ⋅=+D .22023iz在复平面内对应的点位于第一象限试卷第3页,共6页11.已知向量)a = ,()()cos ,sin 0b θθθπ=≤≤,则下列命题不正确的是()A .若a b ⊥,则tan θ=B .若b 在a,则a 与b 夹角为23πC .与a共线的单位向量只有一个为33⎛ ⎝⎭D .存在θ,使得a b a b+=-12.如图,在菱形ABCD 中,2AB =,π3BAD ∠=,将ABD ∆沿BD 折起,使A 到A ',且点A '不落在底面BCD 内,若点M 为线段A C '的中点,则在ABD ∆翻折过程中,以下命题中正确的是()A .四面体A BCD '-的体积的最大值为1B .存在某一位置,使得BM CD⊥C .异面直线BM 与A D '所成的角为定值D .当二面角A BD C '--的余弦值为13时,2A C '=三、填空题(本题共4个小题,每小题5分,共20分.)13.为迎接创卫考核,现从高二(11)班随机选取两名学生参加问卷调查.已知选中的两名学生都是男生的概率是352,选中的两名学生都是女生的概率是2952,则选中的两名学生是一男一女的概率是;14.有一组样本数据1x ,2x ,…,6x 如右表:由这组数据得到新样本数据1y ,2y ,…,6y ,其中2(1,2,,6)3i i y x c i =+= ,c 为常数,则数据1y ,2y ,…,6y 的方差为;15.嵩岳寺塔位于河南郑州登封市嵩岳寺内,历经1400多年风雨侵蚀,仍巍然屹立,是中国现存最早的砖塔.如图,为测量塔的总高度AB ,选取与塔底B 在同一水平面内的两个测量基点C 与D ,现测得30BCD ∠= ,45BDC ∠=,CD =,在C 点测得塔顶A 的仰角为60 ,则塔的总高度为m ;16.在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,已知2a =,222sin 3sin 2sin A B a C +=,则cos C 的最小值为.1x 2x 3x 4x 5x 6x 567576试卷第4页,共6页四、解答题(本题共6个小题,共70分.解答时要求写出必要的文字说明、证明过程或演算步骤.)17.(本小题10分)某高中学校为了学生的身心健康,加强食堂用餐质量(简称“美食”)的过程中,后勤部门需要了解学生对“美食”工作的认可程度,若学生的认可系数(认可系数=100认可程度平均分)不低于0.85,“美食”工作按原方案继续实施,否则需进一步整改.为此该部门随机调查了600名学生,根据这600名学生对“美食”工作认可程度给出的评分,分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图.(1)求直方图中x 的值和中位数;(2)为了解部分学生给“美食”工作评分较低的原因,该部门从评分低于80分的学生中用比例分配的分层随机抽样的方法随机选取30人进行座谈,求应选取评分在[60,70)的学生人数;(3)根据你所学的统计知识,结合认可系数,判断“美食”工作是否需要进一步整改,并说明理由.18.(本小题12分)如图,四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,侧面11ADD A 为矩形,22AB AD ==,160D DB ∠=︒,1BD AA ==(1)证明:平面ABCD ⊥平面11BDD B ;(2)求三棱锥11D BCB -的体积.试卷第5页,共6页19.(本小题12分)某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下表:消费次数第1次第2次第3次第4次消费5次及以上收费比例10.950.900.850.80该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如下表:消费次数第1次第2次第3次第4次消费5次及以上频数60201055假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:(1)估计该公司一位会员至少消费两次的概率;(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;(3)该公司要从这100位里消费二次和三次的顾客中按消费次数用分层随机抽样方法抽出6人,再从这6人中抽出2人发放纪念品,求抽出的2人中恰有1人消费二次的概率.20.(本小题12分)在如图所示的几何体中,ABE ∆、BCE ∆、DCE ∆都是等腰直角三角形,AB AE DE DC ===,且平面ABE ⊥平面BCE ,平面DCE ⊥平面BCE .(1)求证:AD ∥平面BCE ;(2)求直线AB 与平面EAD 所成角的正弦值.试卷第6页,共6页21.(本小题12分)已知,,a b c 分别为ABC ∆三个内角,,A B C的对边,且cos sin a C C b c -=-.(1)求角A (2)若2c =,角B 的平分线BD 交AC 于点D,且BD =ABC ∆的面积.22.(本小题12分)如图1,在边长为4的菱形ABCD 中,60DAB ∠= ,点,M N 分别是边,BC CD 的中点,1AC BD O = ,AC MN G = .沿MN 将CMN ∆翻折到PMN ∆的位置,连接PA 、PB 、PD ,得到如图2所示的五棱锥P ABMND -.(1)在翻折过程中是否总有平面PBD ⊥平面PAG ?证明你的结论;(2)当四棱锥P MNDB -体积最大时,在线段PA 上是否存在一点Q ,使得平面QMN 与平面PMNQ的位置;若不存在,请说明理由.1-4.CADB 5-8.BABB 9.BC10.ACD 11.BCD 12.ABD13.51314.82715.64316.3417.(1)由图可知:10.0150.020.030.025,0.0110x x ++++=∴=,中位数:()0.50.10.150.252458010800.333-+++⨯=+=.(2)低于80分的学生中三组学生的人数比例为0.1:0.15:0.22:3:4=,则应选取评分在[)60,70的学生人数为:33010234⨯=++(人).(3)由图可知,认可程度平均分为:550.1650.15750.2850.3950.2579.50.8510085⨯+⨯+⨯+⨯+⨯=<⨯=,∴“美食"工作需要进一步整改.18.(1)证明:ABD △中,因为2AB =,1AD =,3BD =所以222AB AD BD =+.所以AD BD ⊥,又侧面11ADD A 为矩形,所以1AD DD ⊥,又1BD DD D = ,BD ,1DD ⊂平面11BDD B .所以AD ⊥平面11BDD B ,又AD ⊂平面ABCD ,所以平面ABCD ⊥平面11BDD B .(2)解:因为AD BC ∥,AD ⊥平面11BDD B ,所以BC ⊥平面11BDD B ,易得1BC =,113B D =13B B =,1160D B B ∠=︒,所以11BB D △的面积11133333224BB D S ==△.三棱锥11D BCB -的体积1111111133313344D BCB C BB D BB D V V S BC --==⋅=⨯⨯=△19.(1)100位会员中,至少消费两次的会员有40位,所以估计一位会员至少消费两次的概率为400.4100=.(2)该会员第1次消费时,公司获得的利润为20015050-=(元),第2次消费时,公司获得的利润为2000.9515040⨯-=(元),所以公司获得的平均利润为5040452+=(元).(3)因为20:10=2:1,所以用分层随机抽样方法抽出的6人中,消费2次的有4人,分别设为1234,,,A A A A ,消费3次的有2人,分别设为12,B B ,从中抽出2人,总的抽取方法有121314A A A A A A ,,,1112,A B A B ,23242122A A A A A B A B ,,,,343132414212A A A B A B A B A B B B ,,,,,,共15种,其中恰有1人消费两次的抽取方法有1112,A B A B ,2122A B A B ,,3132A B A B ,,4142A B A B ,,,共8种,所以抽出的2人中恰有1人消费两次的概率为815P =20.(1)证明:分别取,EB EC 的中点,O H ,连接,,AO DH OH ,设1AB AE DE DC ====,则2EB EC ==,,,AB AE BO OE AO BE ==∴⊥ ,又平面ABE ⊥平面BCE ,平面ABE 平面,BCE BE AO =⊂平面ABE ,AO ∴⊥平面BCE ,同理可证DH ⊥平面BCE ,//AO DH ∴,又因为22AO DH ==,所以四边形AOHD 是平行四边形,//AD OH ∴,又AD ⊄Q 平面,BCE OH ⊂平面BCE ,//AD ∴平面BCE ;(2)如图,取BC 的中点为F ,则OF BE ⊥,以点O 为坐标原点,,,OB OF OA 所在的直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则2222220,0,,,,,,,0,0222222A B D E ⎛⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,则2222BA ⎛=-⎝⎭ ,则2222,0,,AE DE ⎛⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭,设平面ADE 的一个法向量为(),,n a b c =,则2200022022a c b c ⎧=⎪+=⎧⎪⇒⎨⎨+=⎩⎪-=⎪⎩,令1a =,得平面ADE 的一个法向量为()1,1,1n=-,设直线BA 与平面EAD 夹角为θ,则6sin |cos ,|3B BA n BA n A nθ⋅=<>== ,所以直线BA 与平面EAD 夹角的正弦值为6321.(1)在 中,由正弦定理及cos 3sin a C a C b c =-得:()sin cos 3sin sin sin sin A C A C A C C =+-,整理得cos sin 3sin sin A C A C C =,而0πC <<,则cos 31A A =,即π1sin()62A +=,又0πA <<,有ππ7π666A <+<,解得π5π66A +=,所以2π3A =.(2)如图,在ABD △中,由余弦定理得:2222cos AB AD AB AD A BD +-⋅=,即2230AD AD +-=,解得1AD =,因BD 平分ABC ∠,11sin sin 2211sin sin(π)22ABD CBD AB BD ABD AD BD ADBS AB AD BC S CDBC BD CBD CD BD ADB ⋅∠⋅∠====⋅∠⋅-∠ ,即2BC AB CD AD ==,在BDC 中,2222cos 227CD BD BC BDC CD BD CD +-∠=⋅又22227cos cos 27AD BD AB BDC BDA BD AD +-∠=-∠=-=-⋅22727CD =,即23470CD CD --=,而0CD >,解得:73CD =,有103AC AD CD =+=,所以ABC 的面积1110353sin 222323AB AC A S =⋅=⨯⨯⨯.22.(1)在翻折过程中总有平面PBD ⊥平面PAG ,证明:∵点M ,N 分别是边CD ,CB 的中点,又60DAB ∠=︒,∴BD MN ∥,且PMN 是等边三角形,∵G 是MN 的中点,∴MN PG ⊥,∵菱形ABCD 的对角线互相垂直,∴BD AC ⊥,∴MN AC ⊥,∵AC PG G ⋂=,AC ⊂平面PAG ,PG ⊂平面PAG ,∴MN ⊥平面PAG ,∴BD ⊥平面PAG ,∵BD ⊂平面PBD ,∴平面PBD ⊥平面PAG .(2)要使得四棱锥P MNDB -体积最大,只要点P 到平面MNDB ∴当PG ⊥平面MNDB 时,点P 到平面MNDB 3假设符合题意的点Q 存在.以G 为坐标原点,GA ,GM ,GP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系,则()33,0,0A ,()0,1,0M ,()0,1,0N -,(3P ,AG PG ⊥,又AG MN ⊥,且MN PG G ⋂=,MN ⊂平面PMN ,PG ⊂平面PMN ,AG ⊥平面PMN ,故平面PMN 的一个法向量为()11,0,0n =u r,设AQ AP λ=(01λ≤≤),∵(33,0,3AP =- ,()333AQ λλ=-,故)()3313λλ-,∴()0,2,0NM =,)()331,1,3QM λλ=- ,平面QMN 的一个法向量为()2222,,n x y z =,则20n NM ⋅= ,20n QM ⋅=,即)222220,33130,y x y z λλ=⎧⎪⎨-+-=⎪⎩令21z =,所以()220,31y x λλ=⎧⎪⎨=⎪-⎩()()()()211,0,1,0,313131n λλλλ⎛⎫==- ⎪ ⎪--⎝⎭,则平面QMN 的一个法向量()(),0,31n λλ=-,设两平面夹角为θ,则()122110cos 1091n n n n λθλλ⋅==+- 12λ=,故符合题意的点Q 存在且Q 为线段PA 的中点.。
黑龙江省哈六中2014-2015学年高一上学期期末考试 数学 Word版含答案

哈尔滨市第六中学2014—2015学年度上学期期末考试高一数学试题考试时间:120分钟 满分:150分一、选择题:(本大题共12小题,每小题5分,共60分)1.已知集合}1,)21(|{},1,log |{2>==>==x y y B x x y y A x,则A =B ( )A . ⎭⎬⎫⎩⎨⎧<<210|y y B. {}10|<<y y C. ⎭⎬⎫⎩⎨⎧<<121|y y D. Φ 2.设()2log log ,2log ,3log 3232===c b a ,则 ( ) A.a b c << B. b c a << C. a c b << D.b a c <<3.在ABC ∆中,60C =,AB =BC =,则A 等于( ) A.135 B.105 C. 45 D. 754.化简22cos 5sin 5sin 40cos 40-=( ) A. 1 B.2 C.12D.1- 5.定义在R 上的函数()f x 满足()()0f x f x +-=,当0m >时,()()f x m f x ->,则不等式2(2)()0f x f x -++<的解集为( )A. (2,1)-B. (,2)(1,)-∞-⋃+∞C. (1,2)-D.(,1)(2,)-∞-⋃+∞6.将函数)42sin(3π-=x y 的图象经过( )变换,可以得到函数x y 2sin 3=的图象A. 沿x 轴向右平移8π个单位 B. 沿x 轴向左平移8π个单位 C. 沿x 轴向右平移4π个单位 D. 沿x 轴向左平移4π个单位7.已知tan 2α=-,且满足42ππα<<,则⎪⎭⎫ ⎝⎛+--απαα4sin 21sin 2cos 22值( )A .2B .-2C .223+-D .223- 8.已知函数()()⎪⎭⎫ ⎝⎛<>>∈+=200sin πϕωϕω,,,A R x x A x f 的图象(部分)如图所示,则()x f 的解析式是 ( ) A .()2sin()()6f x x x R ππ=+∈ B.()2sin(2)()6f x x x R ππ=+∈C.()2sin()()3f x x x R ππ=+∈ D.()2sin(2)()3f x x x R ππ=+∈9.)(x f 是R 上的偶函数,当0≥x 时,有(2)()f x f x +=-,且当[0,2)x ∈时,2()log (1)f x x =+,则)()2012()2011(=+-f f A. 21log 3+ B. 21log 3-+ C.-1 D.110.函数)0(cos sin 3)(>+=ωωωx x x f 与直线2=y 的两个相邻的交点距离等于π,则)(x f 的单调递增区间是( )(A )Z k k k ∈+-],125,12[ππππ (B )Z k k k ∈+-],12,125[ππππ(C )Z k k k ∈+-],6,3[ππππ (D )Z k k k ∈++],32,6[ππππ 11.已知函数()sin()(,0)4f x x x R πωω=+∈>的最小正周期为π,将()y f x =的图象向左平移ϕ个单位长度,所得图象关于y 轴对称,则ϕ的一个值是( )A.2π B. 38π C.4π D.8π12.设()f x 是定义在R 上的偶函数,且(2)(2)f x f x +=-,当[2,0)x ∈-时,()()12xf x =-,若函数()()log (2)a g x f x x =-+(0a >且1a ≠)在区间(2,6)-内恰有4个零点,则实数a 的取值范围是( )A.1(,1)4 B. (1,4) C.(1,8) D. (8,)+∞二、填空题:(本大题共4小题,每小题5分,共20分)13.关于x 的方程2cos sin 0x x a +-=有实数解,则实数a 的取值范围是__________ 14.已知方程220x ax a -+=的两个根均大于1,则实数a 的取值范围为_____________ 15.已知函数()2sin(2)6f x x π=+,在ABC ∆中,,,a b c 分别是角,,A B C 的对边,若()1a f A =,则b c +的最大值为____________16.关于函数()4sin(2)()3f x x x R π=-∈,有以下命题:(1)4()3y f x π=+是偶函数;(2)要得到()4sin 2g x x =-的图象,只需将()f x 的图象向右平移3π个单位;(3)()y f x =的图象关于直线12x π=-对称;(4)()y f x =在[0,]π内的增区间为511[0,],[,]1212πππ, 其中正确命题的序号为______________三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明,证明过程或解题步骤)17.(本题满分10分)设函数2()log ()x x f x a b =-,且(1)1f =,2(2)log 12f =. (1)求a b ,的值;(2)当[12]x ∈,时,求()f x 的最大值.18.(本题满分12分)已知2sin ()cos(2)tan()(),sin()tan(3)f παπαπααπααπ-⋅-⋅-+=+⋅-+(1)化简()f α;(2)若1(),8f α=且,42ππα<<求cos sin αα-的值;(3)求满足1()4f α≥的α的取值集合.19.(本题满分12分)已知βαt an ,t an 是一元二次方程02532=-+x x 的两根,且),2(),2,0(ππβπα∈∈, (1)求)cos(βα-的值;(2)求βα+的值.20.(本题满分12分)已知函数()4cos sin()16f x x x π=+-(1)求()f x 在区间[,]64ππ-上的最大值和最小值及此时的x 值;(2)求()f x 的单调增区间; (3)若1()2f α=,求sin(4)6πα-21.(本题满分12分)已知在ABC ∆中,,,a b c 分别是角,,A B C 的对边,,且满足1cos cos )2A A A ⋅-=(1)求角A 的大小; (2)若ABC a S ∆==,求,b c 的长。
黑龙江省哈尔滨市第六中学2014-2015学年高一12月月考物理试题(暂无答案)
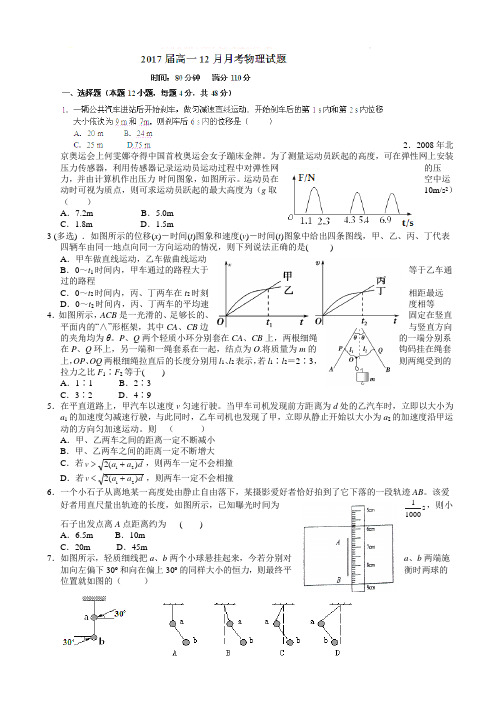
2.2008年北京奥运会上何雯娜夺得中国首枚奥运会女子蹦床金牌。
为了测量运动员跃起的高度,可在弹性网上安装压力传感器,利用传感器记录运动员运动过程中对弹性网的压力,并由计算机作出压力-时间图象,如图所示。
运动员在空中运动时可视为质点,则可求运动员跃起的最大高度为(g 取10m/s 2)( )A .7.2mB .5.0mC .1.8mD .1.5m3 (多选) .如图所示的位移(x )-时间(t )图象和速度(v )-时间(t )图象中给出四条图线,甲、乙、丙、丁代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )A .甲车做直线运动,乙车做曲线运动B .0~t 1时间内,甲车通过的路程大于等于乙车通过的路程C .0~t 2时间内,丙、丁两车在t 2时刻相距最远D .0~t 2时间内,丙、丁两车的平均速度相等4.如图所示,ACB 是一光滑的、足够长的、固定在竖直平面内的“∧”形框架,其中CA 、CB 边与竖直方向的夹角均为θ。
P 、Q 两个轻质小环分别套在CA 、CB 上,两根细绳的一端分别系在P 、Q 环上,另一端和一绳套系在一起,结点为O .将质量为m 的钩码挂在绳套上,OP 、OQ 两根细绳拉直后的长度分别用l 1、l 2表示,若l 1∶l 2=2∶3,则两绳受到的拉力之比F 1∶F 2等于( )A .1∶1B .2∶3C .3∶2D .4∶95.在平直道路上,甲汽车以速度v 匀速行驶。
当甲车司机发现前方距离为d 处的乙汽车时,立即以大小为a 1的加速度匀减速行驶,与此同时,乙车司机也发现了甲,立即从静止开始以大小为a 2的加速度沿甲运动的方向匀加速运动。
则 ( )A .甲、乙两车之间的距离一定不断减小B .甲、乙两车之间的距离一定不断增大C .若d a a v )(221+>,则两车一定不会相撞D .若d a a v )(221+<,则两车一定不会相撞6.一个小石子从离地某一高度处由静止自由落下,某摄影爱好者恰好拍到了它下落的一段轨迹AB 。
黑龙江省哈尔滨市第六中学2015-2016学年高二上学期期中考试数学(文)试题
哈尔滨市第六中学2015-2016学年度上学期期中考试高二数学试题(文史类) 满分:150分 时间:120分钟 第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.1.某学校有高中学生900人,其中高一有400人,高二300人,高三200人,采用分层抽样的方法抽取一个容量为45的样本,那么高一、高二、高三各年级抽取的学生人数为 ( ) A .30、10、5 B .25、15、5 C .20、15、10 D .15、15、152.如图,一个平面图形的斜二测画法的直观图是一个边长为a 的正方形,则原平面图形的面积为( ) A .42a 2 B .a 2 C .22a 2 D .2a 23.给出如下四对事件: ①某人射击1次,“射中7环”与“射中8环”; ②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”; ③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”; ④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”,其中属于互斥事件的有 ( ) A .1对 B .2对 C .3对 D .4对4.已知六棱锥P ABCDEF -的底面是正六边形,PA ⊥平面ABC .则下列结论不正确...的是( )(A )//CD 平面PAF (B )DF ⊥平面PAF (C )//CF 平面PAB (D )CF ⊥平面PAD5.随机对某社区10户居民进行了调查,下表是这10户居民2015年4月份用电量的调,下列说法错误的是( ) A.中位数是55 B .众数是60 C.方差是29 D .平均数是546.一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )A. B .33+C .3D .37.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是( ). A .BD ∥平面CB 1D 1 B.AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1角为60°8.袋中共有6个除了颜色外完全相同的球,其中有1个红球、2个白球和3个黑球.从袋中任取两球,两球颜色为一白一黑的概率等于 ( ) A .15 B .25 C .35 D .459.某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为 ( ) A.2164cm π+ B.2163cm π+ C.2104cm π+ D.2103cm π+10.在正方体1111ABCD A B C D -中,E 是11B C 的中点,则异面直线1DC 与BE 所成角的余弦值为( )A ..510- D. 11.如图,在圆心角为直角的扇形OAB 中,分别以OA ,OB 为直径作两个半圆.在扇形OAB 内随机取一点,则此点取自阴影部分的概率是 ( ) A .112π- B .1π. C .21π- D .2π12的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋最高点与蛋巢底面的距离为 ( )A.32 B .32 C .2322+ D第II 卷(非选择题 共90分)二、填空题:(每小题5分,共20分)13.正方体的表面积为24,则该正方体的内切球的体积为____________.14.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s ,2s ,3s 则它们的大小关系为 .(用“>”连接)15.直三棱柱111C B A ABC -中,︒=∠===120,21BAC AA AC AB ,若各顶点都在同一球面上,则此球的表面积等于 .16.某种游戏中,黑、黄两个“电子狗”从棱长为1的正方体ABCD-A 1B 1C 1D 1的顶点A 出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.黑“电子狗”爬行的路线是AA 1→A 1D 1→ ,黄“电子狗”爬行的路线是AB →BB 1→ ,它们都遵循如下规则:所爬行的第i+2段与第i 段所在直线必须是异面直线(其中i 是正整数).设黑“电子狗”爬完2015段、黄“电子狗”爬完2014段后各自停止在正方体的某个顶点处,这时黑、黄“电子狗”间的距离是 . 三、解答题:(本大题共70分,解答应写出文字说明,证明过程或演算步骤。
黑龙江省哈尔滨市第六中学2010-2011学年度上学期期末考试高二数学理

哈尔滨市第六中学2010—2011学年度上学期期末考试高二(理科)数学试题考试时间:120分钟 满分:150分一、选择题:(每题5分共60分) 1.抛物线x y 102=的焦点到准线的距离是( )A .25 B .5 C .215D .10 2. 下列命题中的假命题是A .1,20x x R -∀∈> B. ∀*x N ∈,2(1)0x -> C .∃ x R ∈,lg 1x < D. ∃x R ∈,tan 2x =3.由曲线x y =2和直线1x =围成图形的面积是 ( )A .3B .23C .34D .324. 设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 A.若l m ⊥,m α⊂,则l α⊥ B.若l α⊥,l m //,则m α⊥ C.若l α//,m α⊂,则l m // D.若l α//,m α//,则l m //5. 函数32y x ax a =-+在(0,1)内有极小值,则实数a 的取值范围是( )A .(0,3) B.⎝ ⎛⎭⎪⎫0,32 C .(0,+∞) D .(-∞,3) 6设双曲线22221(0)x y a b a b-=>>的半焦距为C ,直线L 过(,0),(0,)a b 两点,已知原点到直线L ,则双曲线的离心率为A. 2B. 27. 已知向量(0,2,1),(1,1,2)a b ==--,则a 与b 的夹角为 ( )A . 0°B . 45°C . 90°D .180°8.正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是AA 1、AB 的中点,则EF 与对角面A 1C 1CA 所成角的度数是( )A .30ºB .45ºC .60ºD .150º 9.函数3223125y x x x =--+在区间[0,3]上最大值与最小值分别是( ) A. 5,-15 B. 5,-4 C. -4,-15 D. 5,-16 10.已知直线1y x =+与曲线y ln()x a =+相切,则a 的值为( ) A.1 B. 2 C.-1 D.-211.已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为12. 设a ∈R ,若函数3axy e x =+,x ∈R 有大于零的极值点,则( ) A .3a >-B .3a <-C .13a >-D .13a <-二.填空题:(每题5分共20分)13.如图,已知一四棱锥的主视图、左视图都是等腰直角三角形,俯视图是正方形,则该四棱锥的体积为 14. 函数()ln (0)f x x x x =>的单调递增区间是 . 15.已知⎰-=122)2()(dx x a axa f ,则函数)(a f 的最大值为16. 如图,矩形ABCD 中,DC=3,AD=1,在DC 上截取DE=1,将△ADE 沿AE 翻折到D 1点,点D 1在平面ABC 上的射影落在AC 上时,二面角D 1—AE —B 的平面角的余弦值是 . 三.解答题17. 已知函数()bx ax x x f --=233,其中b a ,为实数. (Ⅰ) 若()x f 在1=x 处取得的极值为2,求b a ,的值;(Ⅱ)若()x f 在区间[]2,1-上为减函数,且a b 9=,求a 的取值范围.(10分)18. 如图在四棱锥P —ABCD 中,底面ABCD 是菱形,∠BAD=600,AB=2,PA=1,PA ⊥平面ABCD ,E 是PC 的中点,F 是AB 的中点。
黑龙江省哈尔滨第六中学2014-2015学年高二上学期期末考试物理试题
黑龙江省哈尔滨第六中学2014-2015学年高二上学期期末考试物理试题3.如图所示,质量分别为m A 和m B 的两小球带有同种电荷,电荷量分别为q A 和q B ,用绝缘细线悬挂在天花板上.平衡时,两小球恰处于同一水平直线上,细线与竖直方向间夹角分别为θ1与θ2(θ1>θ2).现在同时剪断两绝缘细线,下列判断正确的是( )A .m A 一定小于m BB .q A 一定大于q BC .剪断细线后A 、B 两球都沿原细线方向做匀加速直线运动。
D .在两小球落地前观察,同一时刻两小球一定都在同一高度。
4.如图所示,直线MN 是某电场中的一条电场线(方向未画出)。
虚线是一带电粒子只在电场力的作用下,由a 到b 的运动轨迹,轨迹为一抛物线。
下列判断正确的是( )A .电场线MN 的方向一定是由N 指向MB .带电粒子由a 运动到b 的过程中动能一定逐渐减小C .带电粒子在a 点的电势能一定大于在b 点的电势能D .带电粒子在a 点的加速度一定大于在b 点的加速度5. 如图所示,一电子沿x 轴正方向射入电场,在电场中的运动轨迹为OCD ,已知O A =A B ,电子过C 、D 两点时竖直方向的分速度为v Cy 和v Dy ;电子在OC 段和OD 段动能的变化量分别为ΔE k1和ΔE k2,则( )A .v Cy ∶v Dy =1∶2B .v Cy ∶v Dy =1∶4C .ΔE k1∶ΔE k2=1∶3D .ΔE k1∶ΔE k2=1∶46.如图所示,抛物线C 1、C 2分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线.由该图可知下列说法中错误的是( )A .电的电动势为4VB .电的内电阻为1ΩC .电输出功率最大值为8WD .电被短路时,电消耗的最大功率可达16W7.下列关于欧姆表的说法中正确的是( )A .欧姆表的每一档测量范围都是0到“∞”B .红表笔与表内电池负极相联,黑表笔与表内电池正极相联C .“∞”刻度一般在刻度盘的右端D .用欧姆表测电阻时,指针越靠近右边误差越小 MNa b8.下图中平行金属板中带电质点P原处于静止状态,不考虑电流表和电压表对电路的影响,当滑动变阻器R4的滑片向b端移动时,则()A.电压表读数减小 B.电流表读数减小C.质点P将向上运动 D.R3上消耗的功率增大9.如图所示,ab、cd是两根在同一竖直平面内的直导线,在两导线中央悬挂一个小磁针,静止时小磁针和直导线在同一竖直平面内,当两导线中通以大小相等的电流时,小磁针N极向纸面里转动,则两导线中的电流方向()A.一定都是向上 B.一定都是向下C.ab中电流向下,cd中电流向上 D.ab中电流向上,cd中电流向下10.质谱仪是测量带电粒子的质量和分析同位素的重要工具.如图所示为质谱仪的原理示意图.现利用这种质谱议对氢元素进行测量.氢元素的各种同位素从容器A下方的小孔S,无初速飘入电势差为U的加速电场.加速后垂直进入磁感强度为B的匀强磁场中.氢的三种同位素最后打在照相底片D上,形成a、b、c三条“质谱线”.关于三种同位素进人磁场时速度的排列顺序以及a、b、c三条“质谱线”的排列顺序,下列判断正确的是( )A.进入磁场时速度从大到小排列的顺序是氚、氘、氕B.进入磁场时速度从大到小排列的顺序是氘、氚、氕C.a、b、c三条质谱线依次排列的顺序是氘、氚、氕D.a、b、c三条质谱线依次排列的顺序是氚、氘、氕11.如图所示,在光滑水平面上一轻质弹簧将挡板和一条形磁铁连接起,此时磁铁对水平面的压力为N1,现在磁铁正上方位置固定一导体棒,当导体棒中通以垂直纸面向里的电流后,磁铁对水平面的压力为N2 ,则以下说法正确的是( )A.弹簧长度将变长 B.弹簧长度将变短C.N1>N2 D.N1<N212.如右图所示为圆柱形区域的横截面,在没有磁场的情况下,带电粒子(不计重力)以某一初速度沿截面直径方向入射,穿过此区域的时间为t,在该区域加沿轴线垂直纸面向外方向的匀磁强场,磁感应强度大小为B,带电粒子仍以同一初速度沿截面直径入射并沿某一直径方向飞出此区域时,速度方向偏转角为600,如图所示。
黑龙江省哈尔滨市第六中学2015届高三12月月考数学(理)试题
4、设,,αβγ是三个互不重合的平面,,m n 是两条不同的直线,给出下列命题:(1),αββγ⊥⊥,则αγ⊥; (2)若α∥β,m β⊄,m ∥α,则m ∥β;(3)若,m n 在γ内的射影互相垂直,则m n ⊥;(4)若m ∥α,n ∥β,αβ⊥,则m n⊥其中正确命题的个数为( )A .0 B. 1 C. 2 D. 35已知()f x 是定义域为正整数集的函数,对于定义域内任意的k ,若 ()2f k k ≥成立,则()()211f k k +≥+成立,下列命题成立的是 ( )A.若()39f ≥成立,则对于任意1k ≥,均有()2f k k ≥成立;B.若()416f ≥成立,则对于任意的4k ≥,均有()2f k k <成立;C.若()749f ≥成立,则对于任意的7k <,均有()2f k k <成立;D.若()425f =成立,则对于任意的4k ≥,均有()2f k k ≥成立。
6. 已知,,a b c 分别为ABC ∆内角,,A B C 的对边,且,,a b c 成等比数列,且3B π=,则11tan tan A C +=( )A.3B.23C.332D.3347.设数列{}n a 的前n 项和为n S ,11,2(1)()nn Sa a n n N n *==+-∈,若2321(1)402723n S SS S n n ++++--=,则n 的值为( )A 4027B 2013C 2014D 40268.已知实数,x y 满足不等式20403x y x y x -≥⎧⎪+-≥⎨⎪≤⎩,则3322x y x y +的取值范围是( )A 19]3B 1[,2]3C 19[3,]3D 55[3,]99. 已知函数)0,0)(cos()(πθωθω<<>+=x x f 的最小正周期为π,且0)()(=+-x f x f ,若2tan =α,则)(αf 等于( ) A. 54 B. 54- C. 53- D. 53 10.已知正实数b a ,满足12=+b a ,则aba b 2+的最小值为( ) A.221+ B.21+ C.4 D.22 11.给定下列命题:(1) 在△ABC 中,B A ∠<∠是B A 2cos 2cos >的充要条件;(2) λ,μ为实数,若b a μλ=,则a 与b 共线; (3)若向量a ,b 满足|a |=|b |,则a =b 或a =-b ;(4)函数sin 2sin 236y x x ππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭的最小正周期是π; (5)若命题p 为:011>-x ,则011:≤-⌝x p (6)由1131n a a n =,=-,求出123S S S ,,猜想出数列的前n 项和n S 的表达式的推理是归纳推理. 其中正确的命题的个数为:( )A . 1B . 2C . 3D .412.已知函数x xe x f =)(,方程)(01)()(2R t x tf x f ∈=++. 有四个不同的实数根,则t 的取值范围为 ( ).A )1,(2e e +--∞ .B (),2-∞- .C 21,2e e ⎛⎫+-- ⎪⎝⎭.D ),1(2+∞+e e 二、填空题(每题5分共20分)13.已知数列}{n a 满足)2,(*112≥∈=+-n N n a a a n n n ,若4,111164654==++a a a a a ,则 =++654a a a .14.已知四棱锥BCDE A -的底面是边长为2的正方形,面ABC ⊥底面BCDE ,且2==AC AB ,则四棱锥BCDE A -外接球的表面积为________15.在ABC ∆中,已知232BC AC AB AC AB =⋅=⋅,则=∠C _______________16.在△ABC 中,E 为AC 上一点,且4AC AE =,P 为BE 上一点,且满足(0,0)AP mAB nAC m n =+>>,则11m n+取最小值时,向量(),a m n =的模为 .三、解答题17. 已知函数()()21cos cos 02f x x x x ωωωω=+->,其最小正周期为.2π (I )求()f x 的表达式; (II )将函数()f x 的图象向右平移8π个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数()y g x =的图象,若关于x 的方程()0g x k +=,在区间0,2π⎡⎤⎢⎥⎣⎦上有且只有一个实数解,求实数S E DCBA k 的取值范围18. 已知三棱柱ABC —A 1B 1C 1的直观图和三视图如图所示,其主视图BB 1A 1A 和侧视图A 1ACC 1均为矩形,其中AA 1=4。
黑龙江省哈尔滨市第六中学2015届高三10月月考数学(理)试题 Word版含解析
考试时间:120分钟 满分:150分【试卷综析】试卷注重对基础知识和基本方法全面考查的同时,又突出了对数学思想、数学核心能力的综合考查, 试卷以考查考生对“双基”的掌握情况为原则,重视基础,紧扣教材,回归课本,整套试卷中有不少题目可以在教材上找到原型.对中学数学教学和复习回归课本,重视对基础知识的掌握起到好的导向作用.一、选择题:(每题5分共60分)【题文】1.已知全集U R =.集合{}3|<=x x A ,{}0log |2<=x x B ,则U AC B =( )A. {}13x x << B. {}310|<≤≤x x x 或 C. {}3x x < D.{}13x x ≤<【知识点】对数函数的单调性与特殊点;交、并、补集的混合运算.B7 A1 【答案解析】B 解析:由log 2x <0得0<x <1,∴B={x|0<x <1}, ∴U C B ={x|x ≤0或x ≥1},结合A={x|x <3}, ∴U AC B =={x|}={}310|<≤≤x x x 或.故选:B .【思路点拨】先将集合B 进行化简,然后求出其在R 上的补集,再利用交集的定义结合数轴求解.【题文】2. 已知映射B A f →:,其中R B A ==,对应法则21||:x y x f =→,若对实数B k ∈,在集合A 中不存在元素x 使得k x f →:,则k 的取值范围是( )A .0≤kB .0>kC .0≥kD . 0<k 【知识点】映射A1【答案解析】D 解析:由题意可得 k=≥0,∵对于实数k ∈B ,在集合A 中不存在原象,∴k <0,故选D .【思路点拨】先求出k 的值域,则k 的值域的补集即为k 的取值范围. 【题文】3.要得到函数21sin 2+-=x y 的图像,只需将x x y cos sin =的图像( ) A.向左平移4π个单位 B.向右平移4π个单位 C.向左平移2π个单位 D. 向右平移2π个单位【知识点】函数y=Asin (ωx+φ)的图象变换.C4 【答案解析】B 解析:∵函数21sin 2+-=x y =cos2x 又∵y=sinxcosx=sin2x=cos (2x+)∴只需将y=sinxcosx=sin2x=cos (2x+)的图象向右平移个单位即可得到函数y=﹣sin 2x+=cos2x 的图象.故选:B .【思路点拨】将函数用二倍角公式化简,根据函数y=Asin (ωx+φ)的图象变换规律即可解决.【题文】4.下列有关命题的说法正确的是( )A.命题“若21,x =则1x =”的否命题为“若21x =则1x ≠” B .“1x =-”是 “2560x x --=”的必要不充分条件 C. 命题若“x y =”则“sin sin x y =”的逆否命题为真D .命题“2000,10x R x x ∃∈++<”的否定是“对01,2>++∈∀x x R x 。
黑龙江省哈尔滨市第六中学2014届高三9月月考数学(文)试题 Word版含答案
黑龙江省哈尔滨市第六中学2014届高三9月月考数学(文)试题第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分) 1. 集合}12|{Z xN x ∈∈*中含有的元素个数为 ( ) A.4 B. 6 C.8 D. 122. 已知函数⎩⎨⎧≤>=0,30,log )(2x x x x f x ,则))41((f f 的值是( )A. 9B. 91C.9-D. 91- 3. 命题:P 不等式1|1|->-x xx x 的解集为)1,0(;命题:q 在ABC ∆中“B A >”是“B A sin sin >”成立的必要充分条件,则下列命题为真命题的为 ( )A.q p ∧B. q p ∧⌝C.q p ⌝∧D. q p ⌝∧⌝ 4. 已知32cos sin =+θθ,则)252cos(πθ+的值为( ) A.97 B. 97- C. 924- D. 9245. 在△ABC 中,角C B A ,,的对边为,,a b c ,若22241c b a +=,则cBa cos 的值为( ) A.41 B. 45 C. 85 D.83 6.已知函数x x P x f -⋅-=22)(,则下列结论正确的是( )A .1=P ,)(x f 为奇函数且为R 上的减函数B .1-=P ,)(x f 为偶函数且为R 上的减函数C .1=P ,)(x f 为奇函数且为R 上的增函数D .1-=P ,)(x f 为偶函数且为R 上的增函数7. 已知函数()sin()f x A x ωϕ=+,R x ∈(其中πϕπω<<->>,0,0A ),其部分图象如图所示,则ϕω,的值为( )A.4,4πϕπω==B. 43,4πϕπω-==C. 4,2πϕπω==D. 43,2πϕπω-==8. 已知51)4cos(22cos =+πx x ,(π<<x 0)则x tan 的值等于( ) A.34- B. 43-C.2D. 2- 9. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ上单调递减,则ω取值范围是( )A.]45,21[B. ]43,21[C. ]21,0( D. ]2,0( 10.若函数x x x f ln 2)(2-=在其定义域内的一个子区间)1,1(+-k k 内不是单调函数,则实数k 的取值范围是 ( )A. ),1[+∞B. )23,1[C.)2,1[D. )2,23[11. 已知)(x g 为三次函数cx ax x a x f ++=233)(的导函数,则函数)(x g 与)(x f 的图像可能是( )12. 函数)1(|12|)(<-=x x f x 则关于x 的方程0)()(2=++c x bf x f 有个不同实数解的充分条件是( )A.01<<-b 且0>cB. 10<<b 且0<cC.01<<-b 且0=cD. 10<≤b 且0<c二、填空题(本大题共4个小题,每小题5分,共20分)13. 函数)3(log 231x x y -=的单调递减区间是14. 若存在常数m 使得210cos 70sin 32=︒-︒-m ,则实数m 的值为15. 已知函数b a bx ax x f +++=3)(2是定义在]2,1[a a -(R b a ∈,)上的偶函数,则)(x f 的值域为 16.对于函数⎪⎩⎪⎨⎧>+-≤=0,2120,2)(2x x x x xe x f x ,①过该函数图像上一点()2(,2--f )的切线的斜率为22e - ②函数)(x f 的最小值为e2-③该函数图像与x 轴有4个交点④函数)(x f 在]1,(--∞上为减函数,在]1,0(上也为减函数 其中正确命题的序号为第Ⅱ卷(非选择题 共90分)三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤 17. (本小题满分10分)ABC ∆中角C B A ,,的对边分别为c b a ,,,且0222=+-+bc a c b ,(1)求角A 的大小;(2)若3=a ,求ABC ∆面积ABC S ∆的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑龙江省哈尔滨第六中学2014-2015学年高二上学期期末考试数学(理)试题2.从某单位45名职工中随机抽取5名职工参加一项社区服务活动,用随机数表法确定这5名职工.现将随机数表摘录部分如下:16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出的第5个职工的编号为( )(A )23 (B )37 (C )35 (D ) 173.已知向量(1,1,0)a =,(1,0,2)b =-,且ka b +与2a b -互相垂直,则k 的值是( ) (A )1 (B )15 (C ) 35 (D )75 4.已知正四棱柱1111D C B A ABCD -中,AB AA 21=,E 为1AA 中点,则异面直线BE 与1CD 所成角的余弦值为( )(A )1010 (B )10103 (C )51 (D )535.设x Z ∈,集合A 是奇数集,集合B 是偶数集.若命题:,2p x A x B ∀∈∈,则( )(A ):,2p x A x B ⌝∃∈∉ (B ):,2p x A x B ⌝∀∉∉(C ):,2p x A x B ⌝∃∉∈ (D )B x A x p ∉∉∃⌝2,:6.已知点P 是以21,F F 为焦点的椭圆)0(12222>>=+b a by a x 上一点,若021=⋅PF PF ,21tan 21=∠F PF ,则椭圆的离心率为( ) (A )31 (B )21(C )32(D )357.甲、乙两名运动员的5次测试成绩如下图所示设s 1,s 2分别表示甲、乙两名运动员测试成绩的标准差,x 1,x 2分别表示甲、乙两名运动员测试成绩的平均数,则有( )(A )x 1=x 2,s 1<s 2 (B )x 1=x 2,s 1>s 2 (C )x 1>x 2,s 1>s 2 (D )x 1=x 2,s 1=s 28.设n m l ,,表示三条不同的直线,γβα,,表示三个不同的平面,给出下列四个命题: ①若βα⊥⊥⊥m l m l ,,,则βα⊥;②若β⊂m ,n 是l 在β内的射影,n m ⊥,则l m ⊥;③若m 是平面α的一条斜线,α∉A ,l 为过A 的一条动直线,则可能有α⊥⊥l m l 且; ④若γαβα⊥⊥,,则βγ// 其中真命题的个数为( )个(A )1 (B )2 (C )3 (D )49.某四面体的三视图如图所示,三个三角形均为直角三角形,则该四面体的表面积是( ) (A )8(B )34222+ (C )2618+ (D )2624+10.已知两点(10)A ,,(0)B b ,,若抛物线24y x =上存在点C 使ABC ∆为等边三角形,则b =( ) (A )5或31-(B )5 (C )4或2- (D )411.设21,F F 是双曲线)0,0(1:2222>>=-b a by a x C 的两个焦点,P 是C 上一点,若a PF PF 6||||21=+,且21F PF ∆最小内角的大小为︒30,则双曲线C 的渐近线方程是( ) (A )02=±y x (B )02=±y x (C )02=±y x (D )02=±y x12.在球O 的表面上有A B C 、、三个点,若3AOB BOC COA π∠=∠=∠=,且O 到平面ABC 的距离为 )(A )48π (B )36π (C )24π (D )12π第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.将答案写在答题卡上相应的位置 13.袋中有大小相同的红色、白色球各一个,每次任取一个,有放回地摸3次,3次摸到的红球比白球多1次的概率为___________________.14.如图,在直三棱柱111C B A ABC -中,5,4,3===AB BC AC ,点D 是线段AB 上的一点,且︒=∠901CDB ,CD AA =1,则点1A 到平面CD B 1的距离为____________________15.已知双曲线)0,0(12222>>=-b a by a x 的两条渐近线与抛物线)0(22>=p px y 的准线分别交于B A ,两点,O 为坐标原点,若双曲线的离心率为2,AOB ∆的面积为3,则=p ____________.16.如图,从双曲线122=-y x 上一点Q 引直线2=+y x 的垂线,垂足为N ,则线段QN 的中点P 的轨迹方程________________________.三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤 17.(本小题满分10分)直角坐标系xOy 和极坐标系Ox 的原点与极点重合,x 轴正半轴与极轴重合,单位长度相同,在直角坐标系下,曲线C 的参数方程为⎩⎨⎧==ϕϕsin 2cos 4y x ,(ϕ为参数)(1)在极坐标系下,曲线C 与射线4πθ=和射线4πθ-=分别交于A ,B 两点,求AOB ∆的面积;(2)在直角坐标系下,直线l 参数方程为⎪⎩⎪⎨⎧-=-=2226t y tx ,(t 为参数),求曲线C 与直线l 的交点坐标.18.(本小题满分12分)三棱锥BCD A -中,面ACD 与面B C D 均为正三角形,点H G F E ,,,分别为AD AC BC BD ,,,中点(1)证明:四边形EFGH 为矩形;(2)若二面角B DC A --大小为︒60,求直线EH 与面BCD 所成角的正弦值.19.(本小题满分12分)从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.(1)估计这所学校高三年级全体男生身高180cm 以上(含180cm)的人数;(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);ABCDEFGH(3)由直方图估计男生身高的中位数.20.(本小题满分12分)如图,已知椭圆)0(12222>>=+b a by a x ,21,F F 分别为椭圆的左、右焦点,A 为椭圆的上顶点,直线2AF 交椭圆于另一点B . (1)若︒=∠901AB F ,求椭圆的离心率; (2)若F AF 222=,231=⋅AF ,求椭圆的方程.21.(本小题满分12分)四棱锥ABCD P -中,棱长a PD =,底面ABCD 是边长为a 的菱形,点M 为PB 中点(1)若︒=∠90BCP ,证明:PC MD ⊥;(2)若︒=∠90BCD ,︒=∠=∠60PDC PDA ,求二面角A PD B --的余弦值.22.(本小题满分12分)椭圆)0(1:2222>>=+b a by a x G 的左、右焦点为21,F F ,离心率为33,连接椭圆的四个顶点得到的四边形的面积为62,直线1l 过点1F 且垂直于椭圆的长轴,动直线2l 垂直1l 于点P ,线段2PF 的垂直平分线交2l 于点M . (1)求椭圆G 的方程;(2)求点M 的轨迹E 的曲线方程;(3)点B A ,为曲线E 上异于原点O 的两点,OB OA ⊥,=+,求四边形AOBC 的面积最小值.19解:(1)由直方图,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,后三组频率为1-0.82=0.18.这所学校高三男生身高在180cm 以上(含180cm)的人数为800×0.18=144人.…………4分 (2)由频率分布直方图得第八组频率为0.008×5=0.04,人数为0.04×50=2人, 设第六组人数为m ,则第七组人数为0.18×50-2-m =7-m ,又m +2=2(7-m ),所以m =4,即第六组人数为4人,第七组人数为3人,频率分别为0.08,0.06.频率除以组距分别等于0.016,0.012,见图. …………9分 (3)设中位数为n ,由]170,155[频率为32.0,所以)175,170[∈n ,2.032.05.05170-=-n ,解得n =174.5 ………12分20解:若∠F 1AB =90°,则△AOF 2为等腰直角三角形,所以有OA =OF 2,即b =c .所以a =2c ,e =c a =22. …………5分(2)由题知A (0,b ),F 1(-c,0),F 2(c,0),其中,c =a 2-b 2,设B (x ,y ).由=2⇔(c ,-b )=2(x -c ,y ),解得x =3c2,y =-b 2,即B (3c 2,-b 2).将B 点坐标代入x 2a 2+y 2b 2=1,得94c 2a 2+b 24b 2=1,即9c 24a 2+14=1, 解得a 2=3c 2.① 又由·=(-c ,-b )·(3c 2,-3b 2)=32⇒b 2-c 2=1,即有a 2-2c 2=1.②由①,②解得c 2=1,a 2=3,从而有b 2=2. 所以椭圆方程为x 23+y 22=1. …………12分。
