2014中考复习备战(等腰三角形与直角三角形)
2014年中考专题复习 三角形的初步知识

20114年中考专题复习 三角形的初步知识彩虹教育 杨义茂一、考点知识与应用考点一 三角形的性质:1、三角形的内角和是 ,三角形的任意一个外角 和它不相邻两个内角的和,三角形的一个外角 任意一个和它不相邻的内角2、三角形任意两边之和 第三边,任意两边之差 第三边3、三角形具有 性.应用:1、已知三角形的三边长分别是3、x 、9,则化简513x x -+-= ;2、有4根木条,长度分别为6cm ,8cm ,12cm ,20cm ,选其中三根作为边组成三角形,请问:共有多少种组合方法?其中能构成三角形的有几种?3、如图所示,P 为△ABC内任意一点,∠1=∠2,求证:∠ACB与∠BPC互补。
4、如图,在ΔABC 中,∠C=90°,BE 平分∠ABC,AF 平分外角∠BAD,BE 与FA 交与点E 。
求∠E 的度数。
考点二 定义与命题:1、定义:_______________________________________________________________2、命题:_____________________________________________________________应用:1、下列语句:①明天下雨吗? ②中国加油!四川加油!③锐角都相等.④过直线外一点有且只有一条直线和已知直线平行.其中是命题的有( )A、1个 B、2个 C、3个 D、4个 2、下列语句中,属于定义的是( )A 、对顶角相等B 、三角形的内角和等于1800C 、连接A 、B 两点并延长至点CD 、连接三角形两边中点的线段叫做三角形的中位线。
3、下列命题中,是假命题的为( ) A 、邻补角的平分线互相垂直;B 、平行于同一直线的两条直线互相平行;C 、如果一个角的两边平行于另一个角的两边,则这两个角一定相等;D 、平行线的一组内错角的平分线互相平行。
4、有如下命题:①无理数就是开方开不尽的数;②一个实数的立方根不是正数就是负数;③无理数包括正无理数,0,负无理数;④如果一个数的立方根是这个数本身,那么这个数是1或0。
中考数学复习第四章图形的初步认识与三角形第17讲等腰三角形与直角三角形

12
【思路点拨】 本题考查等腰三角形的性质.根据等腰三角形的性质和三角形 的内角和即可得到结论.
第一部分 教材同步复习
13
1.(2017海南)已知△ABC的三边长分别为4,4,6,在△ABC所在平面
内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样
的直线最多可画__________条. A.3
第一部分 教材同步复习
6
(2)在 Rt△ABC 中,∠ACB=90°,∠A=30°,BC=1,则 AB 边上的中线长为
A.1
B.2
(A )
C.1.5
D. 3
(3)已知直角三角形中 30°角所对的直角边为 2 cm,则斜边的长为
(B )
A.2 cm
B.4 cm
C.6 cm
D.8 cm
第一部分 教材同步复习
周长:c=a+b+c;
周长、 面积
面积:SRt△ABC=12ab=12ch(其中
a,b
为两个直角边,c
为斜边,h
为斜边上
的高)
第一部分 教材同步复习
知识点四 等腰直角三角形的判定与性质
【回顾】
(1)等腰直角三角形的直角边为 2,则斜边的长为
A. 2
B.2 2
C.1
D.2
1 (2)等腰直角三角形的斜边长 2,则它的面积为___2_______.
第一部分 教材同步复习
8
(1)有一个角为⑤___9_0_°_____的三角形是直角三角形;
判 (2)勾股定理逆定理:如果三角形的三边长 a,b,c 满足 a2+b2=c2,那么 定 这个三角形是直角三角形;
(3)一条边的中线等于这条边的一半的三角形是直角三角形;
2014年中考数学二轮精品复习试卷(三角形)含答案解析
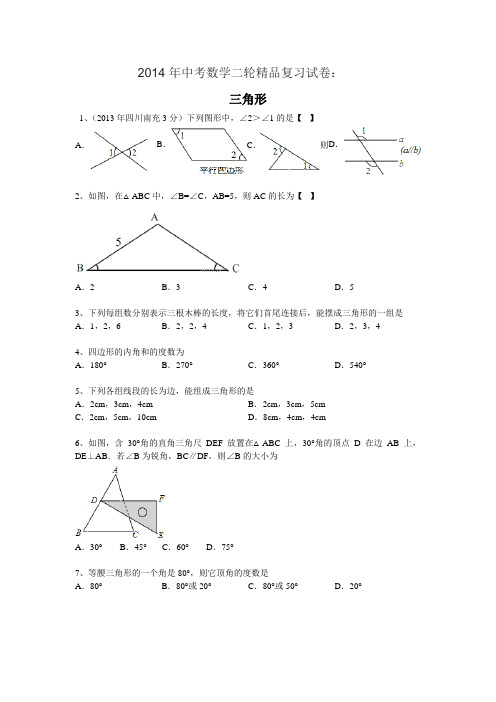
2014年中考数学二轮精品复习试卷:三角形1、(2013年四川南充3分)下列图形中,∠2>∠1的是【】A.B.C.则D.2、如图,在△ABC中,∠B=∠C,AB=5,则AC的长为【】A.2 B.3 C.4 D.53、下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,44、四边形的内角和的度数为A.180°B.270°C.360°D.540°5、下列各组线段的长为边,能组成三角形的是A.2cm,3cm,4cm B.2cm,3cm,5cmC.2cm,5cm,10cm D.8cm,4cm,4cm6、如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB.若∠B为锐角,BC∥DF,则∠B的大小为A.30° B.45° C.60°D.75°7、等腰三角形的一个角是80°,则它顶角的度数是A.80°B.80°或20°C.80°或50°D.20°8、在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,则BD的长为A.B.C.D.9、(2013年四川资阳3分)一个正多边形的每个外角都等于36°,那么它是【】A.正六边形B.正八边形C.正十边形D.正十二边形10、(2013年四川南充3分)如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是【】A.70°B.55°C.50°D.40°11、(2013年广东梅州3分)若一个多边形的内角和小于其外角和,则这个多边形的边数是【】A.3 B.4 C.5 D.612、已知△ABC的各边长度分别为3cm,4cm,5cm,则连结各边中点的三角形的周长为A.2cm B.7cm C.5cm D.6cm13、如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C 的度数为A.50°B.60°C.70°D.80°14、如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为A.B.C.3 D.415、如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为A.20 B.18 C.14 D.1316、如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E 以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t <6),连接DE,当△BDE是直角三角形时,t的值为A.2 B.2.5或3.5 C.3.5或4.5 D.2或3.5或4.517、如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD 于点O,连结AO,下列结论不正确的是【】A.△AOB≌△BOC B.△BOC≌△EOD C.△AOD≌△EOD D.△AOD≌△BOC18、如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a 且AM+MN+NB的长度和最短,则此时AM+NB=A.6 B.8 C.10 D.1219、(2013年四川资阳3分)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是【】A.48 B.60 C.76 D.8020、(2013年四川攀枝花3分)如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC 绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=【】A.30°B.35°C.40°D.50°二、填空题()21、一个六边形的内角和是 .22、如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为米。
中考数学第四篇图形的性质专题18等腰三角形与直角三角形(含解析)(new)

∵AD⊥E′F,但∠E′AD不一定等于∠DAE′,∴△AE′F不一定是等腰三角形,故D错误;
故选D.
考点:1.旋转的性质;2.线段垂直平分线的性质;3.等腰三角形的判定;4.等腰直角三角形;5.正方形的性质;6.相似三角形的判定.
直角三角形
直角三角形的性质
理解直角三角形的有关性质
直角三角形的判定
掌握直角三角形的判定方法,会证明一个三角形是直角三角形
勾股定理
理解并掌握勾股定理及其逆定理
☞2年中考
【2017年题组】
一、选择题
1.(2017内蒙古包头市)若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
=4.故选B.
考点:1.等边三角形的性质;2.含30度角的直角三角形;3.动点型.
10.(2017广西玉林崇左市)如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
考点:1.矩形的性质;2.勾股定理.
21.(2017四川省雅安市)如图,四边形ABCD中,∠A=∠C=90°,∠B=60°,AD=1,BC=2,则四边形ABCD的面积是( )
A. B.3C. D.4
【答案】A.
【解析】
考点:1.勾股定理;2.含30度角的直角三角形;3.解直角三角形.
二、填空题
22.(2017吉林省长春市)如图①,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②,其 中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直 角三角形.若EF=2,DE=8,则AB的长为.
2024年中考数学一轮复习考点课件:等腰三角形与直角三角形

9,12,15 ).
(2) 研究直角三角形的勾股数时,古希腊的哲学家柏拉图曾指出:如
果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三
边的三角形为直角三角形[即(x,y,z)为勾股数],请你加以证明.
解:∵ x2+y2=(2n)2+(n2-1)2=4n2+n4-2n2+1=n4+2n2+1=
B. 15°
C. 20°
D. 25°
考点二
等腰三角形的判定
典例4 如图,下列说法中,正确的是( B )
A. ①是等腰三角形
B. ②是等腰三角形
C. ①和②均是等腰三角形
D. ①和②都不是等腰三角形
典例4图
典例5 (2023·蚌埠模拟)在如图所示的网格中找到格点C,使△ABC为
等腰三角形,则这样的点有( C )
开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形
模型(示意图如图所示),它的顶角为120°,腰长为12m,则底边上的
高是( B )
第4题
A. 4m
B. 6m
1
2
3
C. 10m
4
5
6
7
8
D. 12m
9
10
11
12
13
14
15
5. 如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使
三边相等,即==(如图1)
三个内角相等,每一个角都等于60°,
性质 即∠=∠=∠ = 60° 如图1
等边三角形
等边三角形是轴对称图形,有⑤
三 条对称轴
三条边相等的三角形是等边三角形(定义)
判定 三个角都相等的三角形是等边三角形
2014届中考总复习——等腰三角形与直角三角形

4、角的平分线性质角平分线上的点到 的距离相等
5、角的平分线判定到角两边距离相等的点在
【谈重点】
1、线段的垂直平分可以看作是 的点的集合角平分线可以看作是
的长为
A15
7 B125 C20
7 D21
5
102013?德宏州在Rt△ABC中∠C=90°AB=10若以点C为圆心CB为半径的圆恰
好经过AB的中点D则AC=
A5 B52 C53 D6
112013?大庆正三角形△ABC的边长为3依次在边AB、BC、CA上取点A1、B1、C1使
则∠C的度数为
A50° B60° C70° D80°
对应训练
52013?厦门如图?ABCD的对角线ACBD相交于点O点EF分别是线段AOBO的
中点若AC+BD=24厘米△OAB的周长是18厘米则EF= 厘米
142013?淄博如图△ABC的周长为26点DE都在边BC上∠ABC的平分线垂直于
AE垂足为Q∠ACB的平分线垂直于AD垂足为P若BC=10则PQ的长为
A 3
2 B52 C3 D4
152013?威海如图在△ABC中∠A=36°AB=ACAB的垂直平分线OD交AB于点O
例1 2013?丽水如图在Rt△ABC中∠A=Rt∠∠ABC的平分线BD交AC于点DAD=3
BC=10则△BDC的面积是
对应训练
12013?泉州如图∠AOB=70°QC⊥OA于CQD⊥OB于D若QC=QD则∠AOQ= °
足MN⊥a且AM+MN+NB的长度和最短则此时AM+NB=
A6 B8 C10 D12
【中考备战策略】2014中考数学总复习 第18讲 等腰三角形与直角三角形课件 新人教版
解析: 分两种情况: (1)等腰三角形的腰长为 6 cm, 则它的周长为 6×2+3=15(cm); (2)等腰三角形的腰长 为 3 cm,三角形的三边长分别 6 cm,3 cm,3 cm,不可 能.故选 D.
2.已知等腰三角形的一个内角为 40° ,则这个等 腰三角形的顶角为 ( A. 40° C. 40° 或 100° C ) B. 100° D. 70° 或 50°
考点二 等腰三角形的判定 例 2 (2013· 厦门 )如图,已知 A,B,C,D 是⊙ O 上 的四点,延长 DC, AB 相交于点 E.若 BC= BE. 求证:△ ADE 是等腰三角形.
【点拨】 本题考查圆内接四边形的性质与等腰三角 形的判定. 证明:∵ A, B, C, D 四点共圆, ∴∠ A=∠ BCE. ∵ BC= BE, ∴∠ BCE=∠ E,∴∠ A=∠ E. ∴ AD= DE,即△ ADE 是等腰三角形.
考点二 等腰三角形的性质和判定 1.性质
(1) 等腰三角形的两个 底角 相等 ( 简称: 等边对等 角 ); (2)等腰三角形的顶角平分线、底边上的中线、底 边上的高线互相重合 ; (3)等腰三角形是轴对称 图形,有一 条对称轴,顶 角的平分线 (底边上的中线、 底边上的高线)所在的直线 是它的对称轴.
【点拨】 ∵ AB= BC, ∠ ACB= 35° , ∴∠ A= ∠ ACB = 35° .∵ AB∥ DC, ∴∠ OCD= ∠ A= 35° .∵∠ D= 40° , ∠ AOD 是 △ OCD 的外角, ∴∠ AOD= ∠ OCD+ ∠ D= 35° + 40° = 75° . 【答案】 75°
∵ BE⊥ CE, ∴∠ BCE= 60° , ∠ EBC= 30° . ∴ BC= 2CE. ∵ EA= EC, ∴ BC= AC. ∴△ ABC 是等边三角形.
中考一轮复习--第16讲 等腰、等边与直角三角形
又AD⊥BC,∴△AEF是等腰三角形.∴∠E=∠F;
∵AB=BE,∴∠ABC=2∠E;
同理,得∠ACB=2∠F;∴∠ABC=∠ACB,
即AB=AC,△ABC是等腰三角形;
④在△ABC中,AD⊥BC,根据勾股定理,得
AB2-BD2=AC2-CD2,
即(AB+BD)(AB-BD)=(AC+CD)(AC-CD);
. 35°
解析:在Rt△ABC中,∠ABC=90°,D为AC的中点,∴BD是中
线,∴AD=BD=CD,∴∠DBC=∠C=55°,∴∠ABD=90°-55°=35°.
考法1
考法2
等腰(边)三角形的性质与判定
例2(2019·重庆)如图,在△ABC中,AB=AC,AD⊥BC于点D.
(1)若∠C=42°,求∠BAD的度数;
(2)若点E在边AB上,EF∥AC交AD的延长线于点F.求证:AE=FE.
分析:(1)根据等腰三角形的性质得到∠BAD=∠CAD,根据三角形
的内角和即可得到∠BAD=∠CAD=90°-42°=48°;(2)根据等腰三角形
的性质得到∠BAD=∠CAD,根据平行线的性质得到∠F=∠CAD,等量
代换得到∠BAD=∠F,于是得到结论.
∵∠D=90°,∴CD2+DF2=FC2,
∴CD2+12=32,∴CD=2 2 .
方法总结勾股定理是直角三角形中的一个重要性质,可以由角的
关系得到三角形的边的关系,常用的方法是已知直角三角形的两边
求第三边,或者是已知直角三角形三边之间的关系,列方程求出某
些边长.
考法1
考法2
对应练1(2019·安徽萧县期末)如图,在△ABC
中考复习二次函数中 等腰三角形,直角三角形,平行 四边形的存在问题(图片版 25PPT)
∴所求抛物线的表达式为 y= x2- x-1;
满足条件的 P 为 P1(4, )、P2(-4,7)、P3(2,-1).
5(面积最值)已知抛物线 的图象与 x轴交于点A(3,0) 和点 C,与y 轴交于点B(0,3) 。 (1)求抛物线的解析式。 (2)在抛物线的对称轴上找一点 ,使得点 到点 、 的距离之和 最小,并求出点 的坐标。 (3)在第一象限的抛物线上,是否存在一点 ,使得 的面积最大? 若存在,求出点 的坐标;若不存在,请说明理由。
三、平行四边形的存在问题分类讨论 1. 假设结论成立; 2. 找点:探究平行四边形的存在性问题,一般是已知两定点求未知点坐标,此时可以 分两种情况,分别以这两点所构成的线段为边和对角线来讨论:①以这两点所构成 线段为边时,可以利用平行四边形对边平行且相等,画出符合题意的图形;②以这 两点所构成线段为对角线时,则该线段的中点为平行四边形对角线的交点,结合抛 物线的对称性,画出符合题意的图形; 3. 建立关系式,并计算. 根据以上分类方法画出所有的符合条件的图形后,可以利用 平行四边形的性质进行计算,也可以利用抛物线的对称性、相似三角形或直角三角 形的性质进行计算,要具体情况具体分析,有时也可以利用直线的解析式联立方程 组,由方程组的解为交点坐标的方法求解.
(1)
(2)
(等腰三角形)3、如图,点 A在 x轴上,OA=4 ,将线段 OA绕点 O顺时针旋转120度 至OB 的位置。 (1)求点B 的坐标。 (2)求经过点A 、O 、B 的抛物线的解析式。 (3)在此抛物线的对称轴上,是否存在点P ,使得以 点 P、O 、B 为顶点的三角形是等腰三角形?若存在, 求点P 的坐标;若不存在,说明理由。
面积最值
面积最值
面积最值
不积跬步 无以至千里, 不积小流无以 成江海.
中考总复习之等腰三角形与直角三角形
中考总复习之等腰三角形与直角三角形在中考数学中,等腰三角形与直角三角形是两个非常重要的几何图形,它们的性质和定理在解题中经常被用到。
接下来,让我们一起深入复习这两个重要的知识点。
一、等腰三角形1、定义等腰三角形是指至少有两边相等的三角形。
相等的两条边称为这个三角形的腰,另一边称为底边。
两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
2、性质(1)等腰三角形的两个底角相等(简写成“等边对等角”)。
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)。
(3)等腰三角形是轴对称图形,对称轴为底边上的高(或顶角平分线或底边上的中线)所在的直线。
3、判定(1)如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
(2)有两条边相等的三角形是等腰三角形。
在解决等腰三角形相关问题时,往往需要分类讨论。
比如,已知等腰三角形的一个角的度数,求其他角的度数时,需要分这个角是顶角还是底角两种情况进行讨论。
例 1:已知等腰三角形的一个内角为 70°,求另外两个角的度数。
当 70°角为顶角时,底角的度数为:(180° 70°)÷ 2 = 55°;当 70°角为底角时,另一个底角也是 70°,顶角的度数为 180° 70°×2 = 40°。
例 2:在等腰三角形 ABC 中,AB = AC,BD 是 AC 边上的中线,若△ABD 的周长为 12,△BCD 的周长为 15,求这个等腰三角形的腰长和底边长。
设腰长为 x,底边长为 y,则 AD = CD = x/2。
根据题意可得:x + x/2 + BD = 12 ①y + x/2 + BD = 15 ②②①可得:y x = 3 ③又因为 2x + y =周长(已知)将③变形为 y = x + 3 代入上式,可求出 x 和 y 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点知识梳理
中考典例精析
基础巩固训练
考点训练
温馨提示 1.勾股定理的逆定理是识别一个三角形是否是直 角三角形的一种理论依据,在运用时,一定要用两短 边的平方和与长边的平方作比较 . 2.能够成为直角三角形三条边长的三个正整数, 称 为勾股数 .
考点知识梳理
中考典例精析
基础巩固训练
考点训练
3.若 a,b,c 为一直角三角形的三边长,则以 ma, mb, mc m> 0为三边的三角形也是直角三角形 . 4.如果一个三角形一边上的中线等于这条边的一 半,那么这个三角形是直角三角形 .
考点知识梳理 中考典例精析 基础巩固训练 考点训练
温馨提示 这个性质简称 “三线合一 ”,但不能简单地说成 “等腰三角形的高线、中线、角平分线三线合一 ”.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
2.判定:(1)定义法;(2)如果一个三角形有两个角 相等, 那么这两个角所对的边也相等(简称: 等角对等 边). 温馨提示 等腰三角形的判定定理,是证明两条线段相等的 重要定理,是把三角形中的角的相等关系转化为边的 相等关系的重要依据.
考点五
直角三角形的性质和判定
1.性质 (1)直角三角形的两个锐角互余; (2)在直角三角形中,如果有一个锐角等于 30° ,那
么它所对的直角边等于斜边的一半; (3)直角三角形斜边上的中线等于斜边的一半; (4)勾股定理:直角三角形两直角边 a,b 的平方和 等于斜边 c 的平方,即 a2+b2=c2.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点二 等腰三角形的性质和判定 1.性质
(1) 等腰三角形的两个 底角 相等 ( 简称: 等边对等 角 ); (2)等腰三角形的顶角平分线、底边上的中线、底 边上的高线互相重合 ; (3)等腰三角形是轴对称 图形,有一 条对称轴,顶 角的平分线 (底边上的中线、 底边上的高线)所在的直线 是它的对称轴.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点二 等腰三角形的判定 例 2 (2013· 厦门 )如图,已知 A,B,C,D 是⊙ O 上 的四点,延长 DC, AB 相交于点 E.若 BC= BE. 求证:△ ADE 是等腰三角形.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
【点拨】 本题考查圆内接四边形的性质与等腰三角 形的判定. 证明:∵ A, B, C, D 四点共圆, ∴∠ A=∠ BCE. ∵ BC= BE, ∴∠ BCE=∠ E,∴∠ A=∠ E. ∴ AD= DE,即△ ADE 是等腰三角形.
考点知识梳理 中考典例精析 基础巩固训练 考点训练
温馨提示 1.三角形三边的垂直平分线交于一点, 这一点到三 角形三个顶点的距离相等 . 2.锐角三角形三边垂直平分线的交点在三角形内 部,直角三角形三边垂直平分线的交点恰是斜边的中 点,钝角三角形三边垂直平分线的交点在三角形的外 部.
考点知识梳理 中考典例精析 基础巩固训练 考点训练
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点一 等腰三角形的性质 例 1 (2013· 绵阳 ) 如图, AC, BD 相交于点 O , AB∥ DC, AB= BC, ∠ D= 40° , ∠ ACB= 35° , 则∠ AOD = _______.
等腰三角形与直角三角形
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点一
等腰三角形的概念及分类
1.有两边 相等的三角形叫做等腰三角形;三条边 都相等的三角形叫做等边三角形. 2.等腰三角形分为:底和腰不相等 的等腰三角形 和等边 三角形.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
温馨提示 1.若题目中没有明确边是底还是腰, 角没有明确是 顶角还是底角,就需要分类讨论 . 2.等腰三角形的两腰必须满足两腰之和大于底, 底 角 α 满足 0° < α< 90° ,顶角 β 满足 0° < β< 180° .
温馨提示 由判定 2可知,在等腰三角形中,只要有一个角 是 60° ,不论这个角是顶角还是底角,这个三角形就是 等边三角形 .也可以根据定义判定 .
考点知识梳理
中考典例精析
基础巩固训练
考训练
考点四
线段垂直平分线的性质
1.经过线段的中点并且垂直于这条线段的直线, 叫做线段的垂直平分线. 2.性质 (1) 线段垂直平分线上的点与这条线段 两个端点 的距离相等; (2)与一条线段两个端点的距离相等的点,在这条 线段的垂直平分线 上.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点三
等边三角形的性质和判定
1.性质:等边三角形的三个内角都相等 ,并且每 一个内角都等于 60° . 2.判定 (1) 三个角 都相等的三角形是等边三角形; (2)有一个角是 60° 的等腰 三角形是等边三角形.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
考点知识梳理
中考典例精析
基础巩固训练
考点训练
【点拨】 ∵ AB= BC, ∠ ACB= 35° , ∴∠ A= ∠ ACB = 35° .∵ AB∥ DC, ∴∠ OCD= ∠ A= 35° .∵∠ D= 40° , ∠ AOD 是 △ OCD 的外角, ∴∠ AOD= ∠ OCD+ ∠ D= 35° + 40° = 75° . 【答案】 75°
考点知识梳理 中考典例精析 基础巩固训练 考点训练
考点三 线段垂直平分线的性质 例 3 (2013· 临沂 )如图,四边形 ABCD 中,AC 垂直 平分 BD,垂足为 E,下列结论不一定成立的是( A. AB= AD B. AC 平分∠ BCD C. AB= BD D.△ BEC≌△ DEC
考点知识梳理
中考典例精析
基础巩固训练
考点训练
温馨提示 勾股定理的使用范围是在直角三角形中,因此可 作高来构造直角三角形 .
考点知识梳理
中考典例精析
基础巩固训练
考点训练
2.判定 (1)有一个角是直角的三角形是直角三角形; (2)有两个角互余 的三角形是直角三角形;
(3)勾股定理的逆定理: 如果三角形的三边长 a, b, c 满足 a2+ b2= c2,那么这个三角形是直角三角形.
