2006年上海市初中毕业生统一学业考试数学试卷及解析

合集下载

2006年中考数学试题汇编及解析探索型问题

2006年中考数学试题汇编及解析探索型问题探索型问题这类问题往往涉及面很广，主要是探索题设结论是否存在，或是否成立，或是让学生自己先猜想结论，再进行研究从而得出正确的结论等等，这些题通常有一定的难度，几乎在全国各地的中考数学试卷中都能见到。

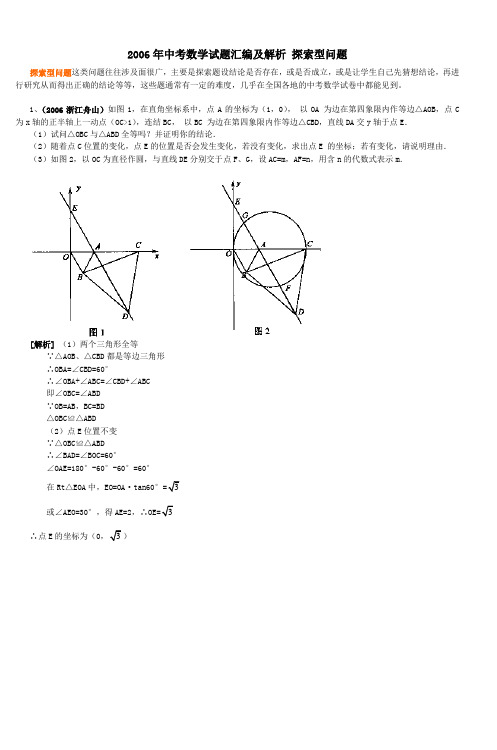
1、（2006浙江舟山）如图1，在直角坐标系中，点A的坐标为（1，0），•以OA•为边在第四象限内作等边△AOB，点C 为x轴的正半轴上一动点（OC>1），连结BC，•以BC•为边在第四象限内作等边△CBD，直线DA交y轴于点E．（1）试问△OBC与△ABD全等吗？并证明你的结论．（2）随着点C位置的变化，点E的位置是否会发生变化，若没有变化，求出点E•的坐标；若有变化，请说明理由．（3）如图2，以OC为直径作圆，与直线DE分别交于点F、G，设AC=m，AF=n，用含n的代数式表示m．[解析]（1）两个三角形全等∵△AOB、△CBD都是等边三角形∴OBA=∠CBD=60°∴∠OBA+∠ABC=∠CBD+∠ABC即∠OBC=∠ABD∵OB=AB，BC=BD△OBC≌△ABD（2）点E位置不变∵△OBC≌△ABD∴∠BAD=∠BOC=60°∠OAE=180°-60°-60°=60°在Rt△EOA中，EO=OA²tan60°或∠AEO=30°，得AE=2，∴∴点E的坐标为（0（3）∵AC=m ，AF=n ，由相交弦定理知1²m=n ²AG ，即AG=m n又∵OC 是直径，∴OE 是圆的切线，OE 2=EG ²EF在Rt △EOA 中，2=（2-m n）（2+n ）即2n 2+n-2m-mn=0解得m=222n nn ++.2、（2006浙江金华）如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式;(2)若S 梯形OBCD ＝3,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的三角形与△OBA 相似.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由. [解析] （1）直线AB 解析式为：y=33-x+3．（2）方法一：设点Ｃ坐标为（x ，33-x+3），那么OD ＝x ，CD ＝33-x+3． ∴OBCD S 梯形＝()2CD CD OB ⨯+＝3632+-x ．由题意：3632+-x ＝334，解得4,221==x x （舍去） ∴ Ｃ（２，33）方法二：∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形＝334，∴63=∆ACD S ．由OA=3OB ，得∠BAO ＝30°，AD=3CD ．∴ ACD S ∆＝21CD ³AD ＝223CD ＝63．可得CD ＝33． ∴ AD=１，OD ＝２．∴C （２，33）．（３）当∠OBP ＝Rt ∠时，如图①若△BOP ∽△OBA ，则∠BOP ＝∠BAO=30°，BP=3OB=3，∴1P （3，33）． ②若△BPO ∽△OBA ，则∠BPO ＝∠BAO=30°,OP=33OB=1． ∴2P （1，3）．当∠OPB ＝Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图)，此时△PBO ∽△OBA ，∠BOP ＝∠BAO ＝30° 过点P 作PM ⊥OA 于点M ．方法一：在Rt △PBO 中，BP ＝21OB ＝23，OP ＝3BP ＝23． ∵ 在Rt △P ＭO 中，∠OPM ＝30°， ∴ OM ＝21OP ＝43；PM ＝3OM ＝433．∴3P （43，433）．方法二：设Ｐ（x ，33-x+3），得OM ＝x ，PM ＝33-x+3 由∠BOP ＝∠BAO,得∠POM ＝∠ABO ．∵tan ∠POM==OMPM =x x 333+-，tan ∠ABOC=OBOA =3．∴33-x+3＝3x ，解得x ＝43．此时，3P （43，433）．④若△POB ∽△OBA(如图)，则∠OBP=∠BAO ＝30°，∠POM ＝30°． ∴ PM ＝33OM ＝43． ∴ 4P （43，43）（由对称性也可得到点4P 的坐标）．当∠OPB ＝Rt ∠时，点P 在ｘ轴上,不符合要求.综合得，符合条件的点有四个，分别是：1P （3，33），2P （1，3），3P （43，433），4P （43，43）．3、（2006湖南常德）如图，在直角坐标系中，以点A 为圆心，以x 轴相交于点B C ，，与y 轴相交于点D E ，．（1）若抛物线213y x bx c =++经过C D ，两点，求抛物线的解析式，并判断点B 是否在该抛物线上．（2）在（1）中的抛物线的对称轴上求一点P ，使得PBD △的周长最小．（3）设Q 为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点M ，使得四边形BCQM 是平行四边形．若存在，求出点M 的坐标；若不存在，说明理由．[解析] （1）OA =∵AB AC ==(B ∴，C又在Rt AOD △中，AD =OA =3OD ==∴D ∴的坐标为(03)-，又D C ，两点在抛物线上，23103c c =-⎧⎪⎨++=⎪⎩ ∴解得3b c ⎧=⎪⎨⎪=-⎩ ∴抛物线的解析式为：21333y x x =--当x =0y = ∴点(B 在抛物线上（2）2133y x x =-∵21(43x =- ∴抛物线2133y x x =-的对称轴方程为x = 在抛物线的对称轴上存在点P ，使PBD △的周长最小．BD ∵的长为定值 ∴要使PBD △周长最小只需PB PD +最小．连结DC ，则DC 与对称轴的交点即为使PBD △周长最小的点．设直线DC 的解析式为y mx n =+．由30n n =-⎧⎪⎨+=⎪⎩得3m n ⎧=⎪⎨⎪=-⎩∴直线DC的解析式为3y x =-由3y x x ⎧=-⎪⎨⎪=⎩得2x y ⎧=⎪⎨=-⎪⎩ 故点P的坐标为2)-（3）存在，设)Q t为抛物线对称轴x =M 在抛物线上要使四边形BCQM 为平行四边形，则BC QM ∥且BC QM =，点M 在对称轴的左侧．于是，过点Q 作直线L BC ∥与抛物线交于点()m M x t ，由BC QM =得QM =从而m x =-，12t =故在抛物线上存在点(M ，使得四边形BCQM 为平行四边形．4、（2006湖南常德）把两块全等的直角三角形ABC 和DEF 叠放在一起，使三角板DEF 的锐角顶点D 与三角板ABC的斜边中点O 重合，其中90ABC DEF ∠=∠= ，45C F ∠=∠=，4AB DE ==，把三角板ABC 固定不动，让三角板DEF 绕点O 旋转，设射线DE 与射线AB 相交于点P ，射线DF 与线段BC 相交于点Q ．（1）如图9，当射线DF 经过点B ，即点Q 与点B 重合时，易证APD CDQ △∽△．此时，APCQ =· ．（2）将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转，设旋转角为α．其中090α<< ，问AP CQ ·的值是否改变？说明你的理由．（3）在（2）的条件下，设CQ x =，两块三角板重叠面积为y ，求y 与x 的函数关系式．[解析] （1）8（2）APCQ ·的值不会改变．理由如下：在APD △与CDQ △中，45A C ∠=∠=18045(45)9A P D a a ∠=--+=-90CDQ a ∠=-ＢＥE 图1 图3图3Ｅ即APD CDQ ∠=∠APD CDQ ∴△∽△AP CDAD CQ=∴22182A P C QA D C D A D A C⎛⎫==== ⎪⎝⎭∴ （3）情形1：当045a <<时，24CQ <<，即24x <<，此时两三角板重叠部分为四边形DPBQ ，过D 作DG AP⊥于G ，DN BC ⊥于N ，2D GD N ==∴ 由（2）知：8AP CQ = 得8AP x=于是111222y AB AC CQ DN AP DG =--88(24)x x x=--<<情形2：当4590a <≤时，02CQ <≤时，即02x <≤，此时两三角板重叠部分为DMQ △，由于8AP x =，84PB x=-，易证：PBM DNM △∽△， B M P B M N D N =∴即22BM PB BM =-解得28424PB x BM PB x-==+- 84444xMQ BM CQ x x-=--=---∴于是1844(02)24xy MQ DN x x x-==--<- ≤ 综上所述，当24x <<时，88y x x=--当02x <≤时，8444xy x x-=---2484y x x x =⎛⎫-+ ⎪-⎝⎭或法二：连结BD ，并过D 作DN BC ⊥于点N ，在DBQ △与MCD △中，45DBQ MCD ∠=∠=45DQB QCB QDC QDC MDQ QDC MDC ∠=∠+∠=+∠=∠+∠=∠DBQ MCD ∴△∽△ M CD B C D B Q=∴4x =- 84MC x =-∴ 284844x x MQ MC CD x x x-+=-=-=--∴ＢＧ2148(02)24x x y DN MQ x x-+==<- ∴≤法三：过D 作DN BC ⊥于点N ，在Rt DNQ △中，222D Q D N NQ =+ 24(2)x =+- 248x x =-+于是在BDQ △与DMQ △中45DBQ MDQ ∠=∠= DMQ DBM BDM ∠=∠+∠ 45BDM =+∠ BDQ =∠BDQ DMQ ∴△∽△BQ DQDQ MQ =∴即4x DQDQ MQ-= 224844DQ x x MQ x x-+==--∴2148(02)24x x y DN MQ x x-+==<- ∴≤5、（2006湖北宜昌）如图，点O 是坐标原点，点A （n ，0）是x 轴上一动点(n ＜0）以AO 为一边作矩形AOBC ，点C 在第二象限，且OB ＝2OA ．矩形AOBC 绕点A 逆时针旋转90o得矩形AGDE ．过点A 的直线y ＝kx ＋m 交y 轴于点F ，FB ＝FA ．抛物线y=ax 2+bx+c 过点E 、F 、G 且和直线AF 交于点H ，过点H 作HM ⊥x 轴，垂足为点M ．(1)求k 的值；(2)点A 位置改变时，△AMH 的面积和矩形AOBC 的面积的比值是否改变？说明你的理由．[解析] （1）根据题意得到：E （3n ，0）， G （n ，－n ）当x ＝0时，y ＝kx ＋m ＝m ，∴点F 坐标为（0，m ）∵Rt △AOF 中，AF 2＝m 2＋n 2， ∵FB ＝AF ，∴m 2＋n 2＝(-2n －m)2，化简得：m ＝－0.75n ，对于y ＝kx ＋m ，当x ＝n 时，y ＝0， ∴0＝kn －0.75n ， ∴k ＝0.75（2）∵抛物线y=ax 2+bx+c 过点E 、F 、G ，∴ ⎪⎩⎪⎨⎧=-++=-++=c c nb a n n c nb a n 75.039022解得：a ＝n 41，b ＝－21，c ＝－0.75n∴抛物线为y=n 41x 2－21x －0.75n解方程组：⎪⎩⎪⎨⎧-=--=nx y n x x n y 75.075.075.021412 得：x 1＝5n ，y 1＝3n ；x 2＝0，y 2＝－0.75n∴H 坐标是：（5n ，3n ），HM ＝－3n ，AM ＝n －5n ＝－4n ，∴△AMH 的面积＝0.5³HM ³AM ＝6n 2；而矩形AOBC 的面积＝2n 2，∴△AMH 的面积∶矩形AOBC 的面积＝3:1，不随着点A 的位置的改变而改变． 6、（2006山东日照）如图（1），在以AB 为直径的半圆O 内有一点P ，AP 、BP 的延长线分别交半圆O 于点C 、D ．求证：AP ²AC+BP ²BD=AB 2．证明：连结AD 、BC ，过P 作PM ⊥AB ，则∠ADB =∠AMP =90ｏ，∴点D 、M 在以AP 为直径的圆上；同理：M 、C 在以BP 为直径的圆上．由割线定理得： AP ²AC=AM ²AB ，BP ²BD=BM ²BA ，所以，AP ²AC+BP ²BD=AM ²AB+BM ²AB=AB ²（AM+BM ）=AB 2．当点P 在半圆周上时，也有AP ²AC+BP ²BD=AP 2+BP 2=AB 2成立，那么：（1）如图（2）当点P 在半圆周外时，结论AP ²AC+BP ²BD=AB 2是否成立？为什么？（2）如图（3）当点P 在切线BE 外侧时，你能得到什么结论？将你得到的结论写出来．[解析] （1）成立．证明：如图（2），∵∠PCM=∠PDM=900， ∴点C 、D 在以PM 为直径的圆上， ∴AC ²AP=AM ²MD ，BD ²BP=BM ²BC ， ∴AC ²AP+BD ²BP=AM ²MD+BM ²BC ，由已知，AM ²MD+BM ²BC=AB 2，∴AP ²AC+BP ²BD=AB 2．（2）如图（3），过P 作PM ⊥AB ，交AB 的延长线于M ，连结AD 、BC ，则C 、M 在以PB 为直径的圆上，∴AP ²AC=AB ²AM ，① D 、M 在以PA 为直径的圆上，∴BP ²BD=AB ²BM ，② 由图象可知：AB=AM-BM ，③由①②③可得：AP ²AC-BP ²BD=AB ²（AM-BM ）=AB 2． 7、（2006江西南昌）问题背景；课外学习小组在一次学习研讨中，得到了如下两个命题：①如图1，在正三角形ABC 中，M ，N 分别是AC 、AB 上的点，BM 与CN 相交于点O ，若∠BON =60°．则BM =CN ：②如图2，在正方形ABCD 中，M 、N 分别是CD 、AD 上的点．BM 与CN 相交于点O ，若∠BON =90°．则BM =CN. 然后运用类似的思想提出了如下命题：③如图3，在正五边形ABCDE 中，M 、N 分别是CD ，DE 上的点，BM 与CN 相交于点O ，若∠BON =108°，则BM =CN .任务要求(1)请你从①．②，③三个命题中选择一个进行证明； (2) 请你继续完成下面的探索；①如图4，在正n (n ≧3)边形ABCDEF ⋅⋅⋅中，M ，N 分别是CD 、DE 上的点，BM 与CN 相交于点O ，试问当∠BON 等于多少度时，结论BM =CN 成立(不要求证明)②如图5，在正五边形ABCDE 中，M 、N 分别是DE ，AE 上的点，BM 与CN 相交于点O ，∠BON =108°时，试问结论BM =CN 是否还成立，若成立，请给予证明．若不成立，请说明理由 (I)我选[解析] （1）如选命题①证明：在图1中，∵∠BON =60°∴∠1+∠2=60° ∵∠3+∠2=60°，∴∠1=∠3又∵BC =CA ，∠BCM =∠CAN =60°∴ΔBCM ≌ΔCAN ∴BM =CN（2）如选命题②证明：在图2中，∵∵∠BON =90°∴∠1+∠2=90° ∵∠3+∠2=90°，∴∠1=∠3又∵BC =CD ，∠BCM =∠CDN =90°∴ΔBCM ≌ΔCDN ∴BM =CN （3）如选命题③证明；在图3中，∵∠BON =108°∴∠1+∠2=108° ∵∠2+∠3=108°∴∠1=∠3 又∵BC =CD ，∠BCM =∠CDN =108° ∴ΔBCM ≌ΔCDN ∴BM =CN(2)①答：当∠BON=0(n-2)180n时结论BM =CN 成立．②答当∠BON =108°时。

2006年上海青浦区初三综合试卷

2006年才上海市青浦区初三综合试卷、填空题（本题共12小题，每小题3分，满分36 分）1、计算a22、若x 5，则..(x -5)2 = ____________3、因式分解：a2 _4b2 = __________4、函数y = . 5 - x的定义域是 ___________ .一k -15、函数y 的图象的两个分支分别在第二、四象限内，则k的取值范围是___________xx2 _2x6、当x = __________ 时，分式-一仝的值为零.x7、方程x • 1 = 2的解是____________8、为了解决药品价格过高的问题，本市决定大幅度降低药品价格，其中将原价为m元的某种常用药降价20%则降价后此药价格为______________9、梯形的中位线长为 4 cm，高为6cm，则该梯形的面积为______________10、已知两个相似三角形的周长比是1:3，则它们的面积比是____________11、如图，PA、PB是O O的两条切线，切点是A、B ,如果OP =4, • APB =60，那么O O的半径是 _________12、如图，把一个直角三角形ACB绕着30角的顶点B 顺时针旋转，使点A与CB的延长线上的点E重合，、选择题（本大题共4题，每小题4分，满分16分）[本题每小题所列出的四个选项中，只有一个是正确的，把正确答案的代号填入括号内] 13、下列说法正确的是这时.BDC的度数是____________A)2§是分数B）实数a的倒数是丄a当.ABC =90时，它是矩形16、已知O 和o O 2的半径分别为4 cm 和3cm ，圆心距02 = 5 cm ,的公切线的条数为三、(本大题共5题，第17、18题每题9分，第19~21题每题10分，满分48分)— x -11 17、已知X 二、2，求(1 )的值.x x18、已知方程x 2 -3x -1 = 0的两根为x 1、 x _3y = 1iX 2 _3xy _4y 2 =0C )负数没有平方根D )绝对值等于本身的数是正数14、将二次函数y = _x 2的图象向右平移 3个单位，再向上平移2个单位,那么所得的二次函数解析式为2A ) y - -(x 3)2 B ) y - -(x-3)2 2 C ) y = _(x 2)23 D )y = -(x -2)23 15、如图，已知四边形 ABCD 是平行四边形,F 列结论中，不正确的是当AB = BC 时，它是菱形当AC _ BD 时，它是菱形D ) 当AC 二BD 时，它是等腰梯形x 2 x 1X 2，求—'—的值. x 1 x 219、解方程组:20、如图，河旁有一座小山，从山顶A处测得河对岸点C的俯角为30，测得岸边点D的俯角为45，现从山顶A到河对岸点C拉一条笔直的缆绳AC，如果AC =120米，求河宽CD的长.21、如图，矩形AOBC，以O为坐标原点，OB、OA分别在x轴、y轴上，点A的坐标为（0, 3），点B的坐标为（5, 0），点E是BC边上一点，如把矩形AOBC沿AE翻折后, C点恰好落在x轴上点F处.（1）求点F的坐标；（2）求线段AF所在直线的解析式.四、（本大题共4题，第22、23、24题每题12分，第25题14分，满分50分）22、为了迎接初三数学学业考试，这学期共进行了10次数学专题测验，其中小丽的数学专题测验成绩情况如图所示:成绩利用图中提供的信息，解答下列问题：(1)____________________________________________ 小丽这10次数学专题测验成绩的平均数为 __________________________________________________ 、中位数为_______ 、方差为______(2)如果将90分以上(含90分)成绩视为优秀，则小丽这10次数学专题测验成绩的优秀率是____________ ；(3)根据以上信息，请你对小丽同学提一条学习建议.23、如图，已知O O的弦AB垂直于直径CD,垂足为F，连接CA、CB .(1) 求证：CAB=/CBA;(2) 在AB上有一点E，延长EC到点P，连接PB ,若EA=EC , PB=PE，求证：PB是O O的切线.24、如图，已知二次函数y = x2 +bx+c的图象经过点A(—2 , 0 )、B(3, 0 )，与y轴交于点C •25、如图，等边三角形ABC的边长为3,点P、Q分别是AB、BC上的动点(点P、Q与三角形ABC的顶点不重合)，且AP =BQ , AQ、CP相交于点E •(1) 如设线段AP为x，线段CP为y，求y关于x的函数解析式，并写出定义域；(2) 当厶CBP的面积是厶CEQ的面积的2倍时，求AP的长；(3) 点P、Q分别在AB、BC上移动过程中，AQ和CP能否互相垂直？如能，请指出P点的位置；如不能，请说明理由.。

2006上海嘉定

2006年嘉定区九年级数学学业考试模拟试卷1. 9的平方根是 .2. 计算：)2)(2(b a b a -+= .3. 函数1)(-=x xx f 的定义域是 . 4. 已知1x 、2x 是方程0422=-+x x 的两个根，则=+21x x . 5. 点P )2,1(-关于x 轴对称的点的坐标为 . 6. 若反比例函数xky =的图象经过点A )2,1(--，则此函数解析式为 . 7. 若二次函数322++=ax x y 的对称轴是直线1=x ，则a = . 8. 若一组数据1、2、4、5、a 的平均数是4，则数a 为 .9. 已知菱形的两条对角线的长分别为32、2，则此菱形的边长是 . 10. 在直角∆ABC 中，C ∠=900，AC=8，21=tgA ，则BC= . 11. 半径分别为2cm 和3cm 两圆的圆心距为1cm ，则这两圆的公切线共有条.12. 在Rt ∆ACB 中，∠C=900，∠A=300，点D （与点A 不重合）在边AC 上，且AD<CD ，若经过点D 的直线截∆ACB 所得的三角形与∆ACB 相似，则这样的直线共有条. 二、选择题（本题共4题，每题4分，满分16分）13. 在下列化简中，正确的是（）（A ）422a a a =+（B ）532a a a =⋅-（C ）a a a -=-÷-23)()(（D ）632)(a a =- 14. 一次函数12--=x y 的图象不经过下列各象限中的（）（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限15. 下列命题中，假命题的是（）（A ）平行四边形的对角线互相平分（B ）对角线互相平分的四边形是平行四边形（C ）矩形的对角线相等（D ）对角线相等的四边形是矩形16. 下列图形中是中心对称图形，但不是轴对称图形的是（）（A ）角（B ）线段（C ）等边三角形（D ）平行四边形三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分） 17. 计算：200)13()4(13230cos 2+--+-+π18. 解方程组：⎩⎨⎧=-+-=+0125222y xy x y x19. 最近某学校九年级某班的学生进行了一次数学测验，其成绩大致分布情况如图1，此图是频率分布直方图（每组含最低值，但不含最高值）.请根据图形所提供的信息解答下列问题：（1）这个班级的学生共有人；（2）在图1中，频率最小的分数段是；（3）在图1中小长方形的表示的是频率；（4）这些成绩的中位数所在的分数段是；（5）若成绩在80及80分以上的学生为优秀，则这个班的优秀率为（用百分比表示）.图120.如图2：在□ABCD 中，∠A=1400，直线BE 交AD 于点E ，交CD 的延长线于点F ，且DE=DF. 求∠F 的度数.21.如图3：在Rt ∆ACB 中，∠C=900，AC=8，BC=6，CD 是斜边AB 上的高. 若点P 在线段DB 上，连结CP ，APC ∠sin =2524. 求CP 的长.A B CDF图2 E CP B图3四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分） 22.已知关于x 的方程0)12(2=+--m x m mx 有两个不相等的实数根.（1）求m 的取值范围；（2）当m 取最大整数时，求方程的两个根.23.如图4：AB 是⊙O 的直径，点P 是AB 延长线上一点，PD 是⊙O 的切线，切点为点D ，连结OD ，点C 是⊙O 上一点，且PC=PD. （1）求证：直线PC 是⊙O 的切线；（2）连结BC ，CB=BP ，PD=32，求⊙O 的半径.图424.将二次函数22x y =(如图5)向右平移1个单位所得的二次函数的图象的顶点为点D ，并与y 轴交于点A.（1）写出平移后的二次函数的对称轴与点A 的坐标；（2）设平移后的二次函数的对称轴与函数22x y =试判断四边形OABD （3）能否在函数22x y = 的图象上找一点P ，使∆DBP 是以线段DB 为直角边的直角三角形？若能，请求出点P 的坐标；若不能，请简要说明理由.图525.如图6：∆ACB与∆DCE是全等的两个直角三角形，其中∠ACB=∠DCE=900，AC=4，BC=2，点D、C、B在同一条直线上，点E在边AC上.（1）直线DE与AB有怎样的位置关系？请证明你的结论；（2）如图6（1）若∆DCE沿着直线DB向右平移多少距离时，点E恰好落在边AB上，求平移距离DD，；（3）在∆DCE沿着直线DB向右平移的过程中，使∆DCE与∆ACB的公共部分是四边形，设平移过程中的平移距离为x，这个四边形的面积为y，求y与x的函数关系式，并写出它的定义域.DE AC 图6DEAC图6（1）DDEABC备用图嘉定区2005年第二学期初三数学练习卷参考答案与评分意见一、1.3±；2.224b a -；3.1≠x ；4.2-；5.)2,1(--；6.xy 2=；7.1-；8.8；9.2；10.4 11.1；12.3.二、13.C ； 14. A ； 15.D ； 16.D. 三、17.解：原式=)1323(1)13)(13()13(2232++-++-++⨯4分 =3241133--+++ 3分=2- 2分18. ⎪⎩⎪⎨⎧=-+-=+)2(012)1(5222y xy x y x解：由（2）得：1)(2=-y x 1分即1=-y x 或1-=-y x 2分所以原方程组变为：⎩⎨⎧=-=+152y x y x ， ⎩⎨⎧-=-=+152y x y x 2分解这两个方程组得：⎪⎪⎩⎪⎪⎨⎧==343711y x ，⎩⎨⎧==2122y x 4分 19.（1）40；（2）40~50；（3）面积；（4）70~80；（5）40%. 每格2分20.解：∵四边形ABCD 是平行四边形∴AB ∥CF ∴∠3=∠F 2分∵DE=DF ∴∠2=∠F 2分∵∠1=∠2∴∠3=∠1 2分∵∠3+∠1+∠A=18001分∵∠A=1400 ∴∠3=200 2分 ∴∠F=200 1分21.解：在Rt ∆ACB 中，∵∠C=900，AC=8，BC=6∴AB=22BC AC +=10 2分 ∵CD 是斜边AB 上的高 ∴CD AB S ABC⨯⨯=∆21又BC AC S ABC ⨯⨯=∆21∴BC AC C D AB ⨯=⨯ 2分∴CD=524 2分在Rt ∆CDP 中，APC ∠sin =CPCD1分∵APC ∠sin =2524∴2524524=CP 1分∴CP=5 2分A B C DF E 13 2 CA D P B四、22.解：（1）∆=[]m m m ⨯⨯---4)12(2 1分 =224144m m m -+-=14+-m 1分根据题意得：14+-m 0> 1分 41<m 2分又0≠m 1分所以m 的取值范围为41<m 且0≠m . 1分（2）根据题意得：1-=m 1分把1-=m 代入原方程得：01)121(2=--⨯---x x 1分即：0132=+-x x 1分解此方程得：2531+=x ，2532-=x 2分所以当m 取最大整数时，此方程的两个根分别是：2531+=x ，2532-=x . 23.（1）证明：连结OC 1分在OPC ∆和OPD ∆中⎪⎩⎪⎨⎧===OP OP PD PC ODOC∴OPC ∆≌OPD ∆（S 、S 、S ）2分 ∴∠OCP=∠ODP 1分 ∵PD 是⊙O 的切线∴OD ⊥PD 1分 ∴∠ODP=900∴∠OCP=900 1分又OC 是⊙O 的半径∴直线PC 是⊙O 的切线 1分（2）∵CB=BP ∴∠1=∠2∵∠OCP=900∴∠4+∠2=900 ∠1+∠3=900∴∠3=∠4 1分 ∴BO=BC 又BO=OC∴OBC ∆是等边三角形 ∴∠3=600 1分 ∵直线PC 是⊙O 的切线 PD 是⊙O 的切线∴PC=PD 1分 ∵PD=32 ∴PC=32 在Rt ∆PCO 中PCOCctg =∠3 1分 ∴32600OCctg =∴OC=2 1分即⊙O 的半径为224.（1）平移后的二次函数的对称轴为直线1=x 1分点A 的坐标（0，2） 1（2）四边形OABD 是矩形. 1 证明：把1=x 代入22x y =得：2=y∴点B 的坐标为（1，2） 1分 2)1(2-=x y∴顶点D 的坐标为（1，0） 1分 ∴OA=DB=2OA ∥BD∴四边形OABD 是平行四边形 1分又∠AOD=900∴四边形OABD 是矩形 1分（3）能. 1分当∠DBP=900时，∵四边形OABD 是矩形∴∠DBA=900 即点P 在直线AB 上，直线AB 为：2=y 把2=y 代入22x y =得：1±=x （正值舍去）即点P 的坐标为)2,1(- 2分当∠PDB=900时，∵四边形OABD 是矩形∴∠BDO=900 即点P 在x 轴上，又点P 在函数22x y =上，所以点P 与点O 重合，即点P 的坐标为)0,0( 2分所以点P 的坐标为)2,1(-、)0,0(25. （1）直线DE 与AB 垂直. 1分证明：延长DE 交AB 于点F∵∆ACB 与∆DCE 是全等的两个直角三角形 ∴∠D=∠A 1分 ∵∠ACB=900∴∠A+∠B=900 ∴∠D+∠B=900 1分 ∴∠BFD=900 1分 ∴直线DE 与AB 垂直.（2）设平移距离DD ，=x则CC ，=x ，BC ，=x -2 1分∵AC ∥E ，C ，∴ACC E BC BC '''=1分又BC=2，EC=E ，C ，=2 AC=4 ∴4222=-x 1分 ∴1=x 1分所以平移距离DD ，为1.DE A C FD EA CD，E，C ，（3）在∆DCE 沿着直线DB 向右平移的过程中第一种情况：如图当点E 落在∆ACB 内部或边AB 上设D ，E ，与边AC 交于点G∵DD ，=x∴CD ，=x -4由题意可知：D ，G ∥DE ∴CDE ∆∽G CD '∆∴2')('CDCD S S G CD CDE =∆∆ 又 CD=4，44221=⨯⨯=∆CDE S ∴2)44(4'xS GCD -=∆ ∴=∆G CD S '4)4(2x - 1分∴4)4(42x y --= ∴x x y 2412+-= 1分定义域为10≤<x 1分第二种情况如图当点E 落在∆ACB 外部，且点C 与点B 重合或在CB 的延长线上，点D 在线段CD 上（与点C 不重合）.设D ，E ，分别交边AC 、AB 于点G 、F 由第一种情况可知：=∆GCD S '4)4(2x -由（1）可知：D ，F ⊥AB∴∠D ，FB =∠ACB=900又∠ABC=∠D ，BF ∴ACB ∆∽FB D '∆ ∴2')('BDAB S S FB D ACB =∆∆ 又 AB=22BC AC +=5244221=⨯⨯==∆∆CDE ACB S S BD ，=x -6 ∴2)652(4'xS FBD -=∆ ∴5)6(2'x S FBD -=∆ 1分 G CD FB D S S y ''∆∆-==4)4(5)6(22x x --- 即：51652202+--=x x y 1分定义域为42<≤x 1分DE A C，GFE，C，D E A BCD，C ，E ，G。

学然教育上海十年中考数学压轴题和答案解析

上海十年中考数学压轴题解析2001年上海市数学中考27．已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．（1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ．图8①求证；△ABP ∽△DPC ②求AP 的长．（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；②当CE ＝1时，写出AP 的长（不必写出解题过程）．27．（1）①证明：∵∠ABP ＝180°－∠A －∠APB ，∠DPC ＝180°－∠BPC －∠APB ，∠BPC ＝∠A ，∴∠ABP ＝∠DPC ．∵在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∴∠A ＝∠D ．∴△ABP ∽△DPC ．②解：设AP ＝x ，则DP ＝5－x ，由△ABP ∽△DPC ，得DCPD AP AB =，即252xx -=，解得x 1＝1，x 2＝4，则AP 的长为1或4．（2）①解：类似（1）①，易得△ABP ∽△DPQ ，∴DQ AP PD AB =．即yxx +=-252，得225212-+-=x x y ，1＜x ＜4．②AP＝2或AP＝3－5．（题27是一道涉及动量与变量的考题，其中（1）可看作（2）的特例，故（2）的推断与证明均可借鉴（1）的思路．这是一种从模仿到创造的过程，模仿即借鉴、套用，创造即灵活变化，这是中学生学数学应具备的一种基本素质，世上的万事万物总有着千丝万缕的联系，也有着质的区别，模仿的关键是发现联系，创造的关键是发现区别，并找到应付新问题的途径．）上海市2002年中等学校高中阶段招生文化考试27．操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．图5图6图7 探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到结论；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由．（图5、图6、图7的形状大小相同，图5供操作、实验用，图6和图7备用）五、（本大题只有1题，满分12分，（1）、（2）、（3）题均为4分）27．图1 图2 图3（1）解：PQ ＝PB ……………………（1分）证明如下：过点P 作MN ∥BC ，分别交AB 于点M ，交CD 于点N ，那么四边形AMND 和四边形BCNM 都是矩形，△AMP 和△CNP 都是等腰直角三角形（如图1）．∴ NP ＝NC ＝MB ． ……………………（1分）∵ ∠BPQ ＝90°，∴ ∠QPN ＋∠BPM ＝90°．而∠BPM ＋∠PBM ＝90°，∴ ∠QPN ＝∠PBM ． ……………………（1分）又∵ ∠QNP ＝∠PMB ＝90°，∴ △QNP ≌△PMB ． ……………………（1分） ∴ PQ ＝PB ．（2）解法一由（1）△QNP ≌△PMB ．得NQ ＝MP ． ∵ AP ＝x ，∴ AM ＝MP ＝NQ ＝DN ＝x 22，BM ＝PN ＝CN ＝1－x 22， ∴ CQ ＝CD －DQ ＝1－2·x 22＝1－x 2．得S △PBC ＝21BC ·BM ＝21×1×（1－x 22）＝21－42x ． ………………（1分） S △PCQ ＝21CQ ·PN ＝21×（1－x 2）（1－x 22）＝21－x 423＋21x 2 （1分）S 四边形PBCQ ＝S △PBC ＋S △PCQ ＝21x 2－x 2＋1．即 y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分，1分）解法二作PT ⊥BC ，T 为垂足（如图2），那么四边形PTCN 为正方形． ∴ PT ＝CB ＝PN ．又∠PNQ ＝∠PTB ＝90°，PB ＝PQ ，∴△PBT ≌△PQN ．S 四边形PBCQ ＝S △四边形PBT ＋S 四边形PTCQ ＝S 四边形PTCQ ＋S △PQN ＝S 正方形PTCN …（2分）＝CN 2＝（1－x 22）2＝21x 2－x 2＋1 ∴ y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分）（3）△PCQ 可能成为等腰三角形①当点P 与点A 重合，点Q 与点D 重合，这时PQ ＝QC ，△PCQ 是等腰三角形，此时x ＝0 ……………………（1分）②当点Q 在边DC 的延长线上，且CP ＝CQ 时，△PCQ 是等腰三角形（如图3） ……………………（1分）解法一此时，QN ＝PM ＝x 22，CP ＝2－x ，CN ＝22CP ＝1－x 22． ∴CQ ＝QN －CN ＝x 22－（1－x 22）＝x 2－1．当2－x ＝x 2－1时，得x ＝1． ……………………（1分）解法二此时∠CPQ ＝21∠PCN ＝22.5°，∠APB ＝90°－22.5°＝67.5°， ∠ABP ＝180°－（45°＋67.5°）＝67.5°，得∠APB ＝∠ABP ，∴AP＝AB＝1，∴x＝1．……………………（1分）上海市2003年初中毕业高中招生统一考试27.如图，在正方形ABCD中，AB＝1，弧AC是点B为圆心，AB长为半径的圆的一段弧。

2006年上海中考数学

2006年上海市中考数学试卷答案一、填空题（共12小题，每小题3分，满分36分）1．2 分析：利用二次根式的性质化简.原式=22=2.2.x 3 分析：因为分母相同，所以分母不变，分子直接相加.x 1+x 2=x3.3.x>6 分析：利用不等式的基本性质，将两边不等式同时加6，不等号的方向不变．得到不等式的解集为：x ＞6.4.x(x+y) 分析：直接提取公因式x 即可.x 2+xy=x （x+y ）.5.x ≠3 分析：根据分式有意义，则故分母x ﹣3≠0，解得x 的范围.则x ﹣3≠0，解得：x ≠3.6.1 分析：本题思路是两边平方后去根号，解方程.两边平方得2x ﹣1=1，解得x=1．经检验x=1是原方程的根．平方时可能产生增根，要验根.7.-4 分析：根据一元二次方程中根与系数的关系即可求解.由根与系数的关系可得x 1•x 2=﹣4.8.y 2﹣2y+1=0 分析：设y=122 x x ，原方程可化为y+y 1=2，方程两边都乘y 得：y 2+1=2y ，整理得y 2﹣2y+1=0.9.5.09 分析：根据图象知道100升油花费了509元，由此即可求出这种汽油的单价.单价=509÷100=5.09元．10.∠B=∠B 1或∠C=∠C 1或AC=A 1C 1（答案不唯一）分析：根据全等三角形的判定（有两边及其夹角对应相等的两个三角形全等SAS ）可得当AC=A 1C 1时可得△ABC ≌△A 1B 1C 1．根据全等三角形的判定（有两角及其夹边对应相等的两个三角形全等ASA ）可得当∠B=∠B 1或∠C=∠C 1（AAS ）△ABC ≌△A 1B 1C 1．根据全等三角形的判定（有两角及其夹边对应相等的两个三角形全等ASA ）可得当∠B=∠B 1或∠C=∠C 1（AAS ）△ABC ≌△A 1B 1C 1．11.3 分析：由圆切线的性质可知OA ⊥PA ，再根据勾股定理即可求得PA 的长.如图，∵PA 是⊙O 的切线，连接OA ，∴OA ⊥PA ，∵OP=2，OA=1，∴PA=22OA OP -=2212-=3.12.如图所示分析：本题可通过画中心对称图形来完成，找出关键点这里半径长，画弧，连接关键点即可.13.A 分析：一元二次方程要有实数根，则△≥0；算术平方根不能为负数；分式方程化简后求出的根要满足原方程.A 、△=9﹣4=5＞0，方程有实数根；B 、算术平方根不能为负数，故错误；C 、△=4﹣12=﹣8＜0，方程无实数根；D 、化简分式方程后，求得x=1，检验后，为增根，故原分式方程无解．故选A.14.B 分析：根据二次函数的顶点式一般形式的特点，可直接写出顶点坐标.二次函数y=﹣（x ﹣1）2+3为顶点式，其顶点坐标为（1，3）．故选B.15.B 分析：根据重心的性质三角形的重心到一顶点的距离等于到对边中点距离的2倍，直接求得结果．∵三角形的重心到顶点的距离是其到对边中点的距离的2倍，∴DG=21AG=3．故选B ．16.D 分析：根据矩形的判定定理解答；B 、根据菱形的判定与性质解答；C 、根据正方形的判定与性质解答；D 、根据平行四边形的性质与判定解答.A 、等腰梯形也满足此条件，但不是矩形；故本选项错误；B 、两条对角线互相垂直平分的四边形才是菱形；故本选项错误；C 、对角线相等的平行四边形是矩形，对角线互相垂直的平行四边形是菱形，既是矩形又是菱形的四边形是正方形，所以两条对角线垂直且相等的平行四边形是正方形；故本选项错误；D 、两条对角线互相平分的四边形是平行四边形；故本选项正确．故选D.17.原式=x x 1+÷xx 12-=x x 1+÷()()x x x 11+-=x x 1+·()()11+-x x x =11-x ，当x=2时，原式=121-=12+. 分析：本题要先将分式化简，再把x 的值代入求解，分式的混合运算，要特别注意运算顺序以及符号的处理.18.⎩⎨⎧=++=--②,01①,032y x y x ①+②得x 2+x ﹣2=0，解得x 1=﹣2，x 2=1，由x 1=﹣2，得y 1=﹣5，由x 2=1，得y 2=﹣2，∴原方程组的解是解是⎩⎨⎧-=-=;5,211y x ⎩⎨⎧-==.2,122y x 分析：这是一道一元二次方程的变形题，观察题可发现两式相加就变成了一元二次方程，然后解一元二次方程即可.19.（1）∵AD 是BC 边上的高，△ABD 和△ACD 是直角三角形，在Rt △ABD 中，∵sinB=54，AD=12，∴AB AD =54，∴AB=15，∴BD=22AD AB -=9，又∵BC=14，∴CD=5；（2）在Rt △ACD 中，∵E 为斜边AC 的中点，∴ED=EC=21AC ，∴∠C=∠EDC ，∴tan ∠EDC=tanC=DC AD =512. 分析：（1）在Rt △ABD 中，根据已知条件求出边AB 的长，再由BC 的长，可以求出CD 的长；（2）根据直角三角形中，斜边上的中线等于斜边的一半，求出∠C=∠EDC ，从而求出∠C 的正切值即求出了tan ∠EDC 的值．此题要灵活应用三角函数公式和解直角三角形的公式，同时还要掌握“直角三角形中，斜边上的中线等于斜边的一半“等知识点.20.（1）9÷15%=60；（2）60﹣9﹣41=10；如图所示；（3）不能，因为所抽取的样本不具有代表性．分析：（1）根据橙色与黄色标识路口数之和是1+8=9，占被调查路口总数的15%，计算总数；（2）根据总数计算绿色标识；（3）根据样本是否具有代表性进行判断.21.设圆心为点O ，联结OB ，OA ，OA 交线段BC 于点D.∵AB=AC ，∴，∴OA ⊥BC ，且BD=DC=21BC=120米，由题意，DA=5米，在Rt △BDO 中，OB 2=OD 2+BD 2，设OB=x 米，则x 2=（x ﹣5）2+1202，解得x=1442.5．答：滴水湖的半径为1442.5米. 分析：根据等弦对等弧，知点A 即是弧BC 的中点．结合垂径定理的推论，知OA 垂直平分弦，设圆的半径，结合垂径定理和勾股定理列出关于半径的方程，即可求得圆的半径.此题综合运用了等弦对等弧、垂径定理的推论、勾股定理.22.（1）由题意，设点A 的坐标为（a ，3a ），a ＞0，∵点A 在反比例函数y=x 12的图象上，得：3a=a12，解得a 1=2，a 2=﹣2，经检验a 1=2，a 2=﹣2是原方程的根，但a 2=﹣2不符合题意，舍去，∴点A 的坐标为（2，6）；（2）设点B 的坐标为（0，m ），∵m ＞0，OB=AB ， ∴在Rt △ABC 中，根据勾股定理得：AB 2=BC 2+AC 2，即m 2=（6﹣m ）2+2 2，解得m=310，经检验m=310是原方程的根，∴点B 的坐标为（0，310），设一次函数的解析式为y=kx+310，由于这个一次函数图象过点A （2，6），∴6=2k+310，解得k=34，∴所求一次函数的解析式为y=34x+310．分析：（1）根据A 点位置及坐标特点，代入反比例函数解析式解方程即可求出A 的坐标；（2）根据题意求B 点坐标，再求解析式.主要考查反比例函数的图象特点和待定系数求函数解析式．23.证明：（1）∵在梯形ABCD 中，AB=DC ，∴∠B=∠C ．∵GF=GC ，∴∠C=∠GFC ，∴∠B=∠GFC ∴AB ∥GF ，即AE ∥GF ．∵AE=GF ，∴四边形AEFG 是平行四边形．（2）∵∠FGC+∠GFC+∠C=180°，∠GFC=∠C ，∠FGC=2∠EFB ，∴2∠GFC+2∠EFB=180°，∴∠BFE+∠GFC=90°．∴∠EFG=90°．∵四边形AEFG 是平行四边形，∴四边形AEFG 是矩形．分析：（1）要证明该四边形是平行四边形，只需证明AE ∥FG ．根据对边对等角∠GFC=∠C ，和等腰梯形的性质得到∠B=∠C ．则∠B=∠GFC ，得到AE ∥FG ．（2）在平行四边形的基础上要证明是矩形，只需证明有一个角是直角．根据三角形FGC 的内角和是180°，结合∠FGC=2∠EFB 和∠GFC=∠C ，得到∠BFE+∠GFC=90°．则∠EFG=90°.此题主要考查了平行四边形的性质与矩形的判定定理和平行线的性质等知识，掌握平行四边形和矩形的判定方法是解题关键.24.（1）由题意，点B 的坐标为（0，2），∴OB=2，∵tan ∠OAB=2，即OA OB =2．∴OA=1．∴点A 的坐标为（1，0）．又∵二次函数y=x 2+mx+2的图象过点A ，∴0=12+m+2．解得m=﹣3，∴所求二次函数的解析式为y=x 2﹣3x+2．（2）作CE ⊥x 轴于点E ，由于∠BAC=90°，可知∠CAE=∠OBA ，△CAE ≌△OBA ，可得CE=OA=1，AE=OB=2，可得点C 的坐标为（3，1）．由于沿y 轴运动，故图象开口大小、对称轴均不变，设出解析式为y=x 2﹣3x+c ，代入C点作标得1=9﹣9+c ，c=1，所求二次函数解析式为y=x 2﹣3x+1．（3）由（2），经过平移后所得图象是原二次函数图象向下平移1个单位后所得的图象，那么对称轴直线x=23不变，且BB 1=DD 1=1．∵点P 在平移后所得二次函数图象上，设点P 的坐标为（x ，x 2﹣3x+1）．在△PBB 1和△PDD 1中，∵S △PBB1=2S △PDD1，∴边BB 1上的高是边DD 1上的高的2倍．①当点P 在对称轴的右侧时，x=2（x ﹣23），得x=3，∴点P 的坐标为（3，1）；②当点P 在对称轴的左侧，同时在y 轴的右侧时，x=2（23﹣x ），得x=1，∴点P 的坐标为（1，﹣1）；③当点P 在y 轴的左侧时，x ＜0，又﹣x=2（23﹣x ），得x=3＞0（舍去），∴所求点P 的坐标为（3，1）或（1，﹣1）．分析：（1）二次函数y=x 2+mx+2的图象经过点B ，可得B 点坐标为（0，2），再根据tan ∠OAB=2求出A 点坐标，将A 代入解析式即可求得函数解析式；（2）根据旋转不变性可轻松求得C 点坐标，由于沿y 轴运动，故图象开口大小、对称轴均不变，设出解析式，代入C 点作标即可求解；（3）由于P 点位置不固定，由图可知要分①当点P 在对称轴的右侧时，②当点P 在对称轴的左侧，同时在y 轴的右侧时，③当点P 在y 轴的左侧时，三种情况讨论.此题是一道中考压轴题，将解直角三角形、图形的旋转和平移以及点的存在性的探索等问题结合起来，考查了综合应用各种知识解题的能力，思维跳跃较大，有一定难度．25. （1）证明：∵AP=2PB=PB+BO=PO ，∴AO=2PO ．∴PO AO =BO PO =2．∵PO=CO ， ∴CO AO =BOCO ．∵∠COA=∠BOC ，∴△CAO ∽△BCO ．（2）设OP=x ，则OB=x ﹣1，OA=x+m ，∵OP 是OA ，OB 的比例中项，∴x 2=（x ﹣1）（x+m ）．∴x=1-m m ．即OP=1-m m ．∴OB=11-m ．∵OP 是OA ，OB 的比例中项，即PO AO =BOPO ，∵OP=OC ，∴CO AO =BOCO ．设⊙O 与线段AB 的延长线相交于点Q ，当点C 与点P ，点Q 不重合时，∵∠AOC=∠COB ，∴△CAO ∽△BCO ．∴BC AC =BO CO ．∴BC AC =BO CO =BOPO =m ．当点C 与点P 或点Q 重合时，可得BCAC =m ，∴当点C 在圆O 上运动时，AC ：BC=m ．（3）由（2）得，AC ＞BC ，且AC ﹣BC=（m ﹣1）BC （m ＞1），AC+BC=（m+1）BC ，⊙B 和⊙C 的圆心距d=BC ，显然BC ＜（m+1）BC ，∴⊙B 和⊙C 的位置关系只可能相交、内切或内含．当⊙B与⊙C相交时，（m﹣1）BC＜BC＜（m+1）BC，得0＜m＜2，∵m＞1，∴1＜m＜2；当⊙B与⊙C内切时，（m﹣1）BC=BC，得m=2；当⊙B与⊙C内含时，BC＜（m﹣1）BC，得m＞2．分析：（1）根据夹角相等，对应边成比例可证；（2）OP是OA，OB的比例中项，OC=OP，△CAO∽△BCO可得．（3）讨论相交，内切，内含与⊙B与⊙C的圆心距的关系.。

上海历年中考数学压轴题复习

上海历年中考数学压轴题复习2001年上海市数学中考27．已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．（1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ．图8①求证；△ABP ∽△DPC②求AP 的长．（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；②当CE ＝1时，写出AP 的长（不必写出解题过程）．27．（1）①证明：∵ ∠ABP ＝180°－∠A －∠APB ，∠DPC ＝180°－∠BPC －∠APB ，∠BPC ＝∠A ，∴ ∠ABP ＝∠DPC ．∵ 在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∴ ∠A ＝∠D ．∴ △ABP ∽△DPC ． ②解：设AP ＝x ，则DP ＝5－x ，由△ABP ∽△DPC ，得DCPD AP AB =，即252x x -=，解得x 1＝1，x 2＝4，则AP 的长为1或4．（2）①解：类似（1）①，易得△ABP ∽△DPQ ，∴ DQ AP PD AB =．即y x x +=-252，得225212-+-=x x y ，1＜x ＜4． ②AP ＝2或AP ＝3－5．（题27是一道涉及动量与变量的考题，其中（1）可看作（2）的特例，故（2）的推断与证明均可借鉴（1）的思路．这是一种从模仿到创造的过程，模仿即借鉴、套用，创造即灵活变化，这是中学生学数学应具备的一种基本素质，世上的万事万物总有着千丝万缕的联系，也有着质的区别，模仿的关键是发现联系，创造的关键是发现区别，并找到应付新问题的途径．）上海市2002年中等学校高中阶段招生文化考试27．操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．图5图6图7探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系试证明你观察得到结论；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由．（图5、图6、图7的形状大小相同，图5供操作、实验用，图6和图7备用）五、（本大题只有1题，满分12分，（1）、（2）、（3）题均为4分）27．图1 图2 图3（1）解：PQ ＝PB ……………………（1分）证明如下：过点P 作MN ∥BC ，分别交AB 于点M ，交CD 于点N ，那么四边形AMND 和四边形BCNM 都是矩形，△AMP 和△CNP 都是等腰直角三角形（如图1）．∴ NP ＝NC ＝MB ． ……………………（1分） ∵ ∠BPQ ＝90°，∴ ∠QPN ＋∠BPM ＝90°．而∠BPM ＋∠PBM ＝90°，∴ ∠QPN ＝∠PBM ． ……………………（1分）又∵ ∠QNP ＝∠PMB ＝90°，∴ △QNP ≌△PMB ． ……………………（1分） ∴ PQ ＝PB ．（2）解法一由（1）△QNP ≌△PMB ．得NQ ＝MP ．∵ AP ＝x ，∴ AM ＝MP ＝NQ ＝DN ＝x 22，BM ＝PN ＝CN ＝1－x 22， ∴ CQ ＝CD －DQ ＝1－2·x 22＝1－x 2．得S △PBC ＝21BC ·BM ＝21×1×（1－x 22）＝21－42x ． ………………（1分） S △PCQ ＝21CQ ·PN ＝21×（1－x 2）（1－x 22）＝21－x 423＋21x 2 （1分） S 四边形PBCQ ＝S △PBC ＋S △PCQ ＝21x 2－x 2＋1．即 y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分，1分）解法二作PT ⊥BC ，T 为垂足（如图2），那么四边形PTCN 为正方形．∴ PT ＝CB ＝PN ．又∠PNQ ＝∠PTB ＝90°，PB ＝PQ ，∴△PBT ≌△PQN ．S 四边形PBCQ ＝S △四边形PBT ＋S 四边形PTCQ ＝S 四边形PTCQ ＋S △PQN ＝S 正方形PTCN…（2分）＝CN 2＝（1－x 22）2＝21x 2－x 2＋1∴ y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分）（3）△PCQ 可能成为等腰三角形①当点P 与点A 重合，点Q 与点D 重合，这时PQ ＝QC ，△PCQ 是等腰三角形，此时x ＝0 ……………………（1分） ②当点Q 在边DC 的延长线上，且CP ＝CQ 时，△PCQ 是等腰三角形（如图3）……………………（1分）解法一此时，QN ＝PM ＝x 22，CP ＝2－x ，CN ＝22CP ＝1－x 22． ∴ CQ ＝QN －CN ＝x 22－（1－x 22）＝x 2－1．当2－x ＝x 2－1时，得x ＝1． ……………………（1分）解法二此时∠CPQ ＝21∠PCN ＝°，∠APB ＝90°－°＝°， ∠ABP ＝180°－（45°＋°）＝°，得∠APB ＝∠ABP ，∴ AP ＝AB ＝1，∴ x ＝1． ……………………（1分）上海市2003年初中毕业高中招生统一考试27.如图，在正方形ABCD 中，AB ＝1，弧AC 是点B 为圆心，AB 长为半径的圆的一段弧。

2006年上海市部分学校初三数学抽样测试卷

2006年上海市部分学校初三数学抽样测试卷（满分150分，考试时间100分钟）一、填空题：（本大题共12题，满分36分）【只要求直接填写结果，每个空格填对得3分，否则得0分】1．2-的相反数是．2．不等式3＋2x ≤9的解集是．3．函数12-=x y 的定义域是 . 4．点Q （－3，4）关于原点对称的点的坐标是．5．三峡水库的库容量可达393 000 000 000立方米，这个数用科学记数法表示为． 6．如果x =1是方程032=+-x ax 的根，那么a ＝．7．如果方程0242=+-x x 的两个实数根分别是x 1、x 2，那么21x x = ．8．平价大药房大幅度降低药品价格，某种常用药品原来价格为m 元，那么降价30%后的价格为元.9．已知两个相似三角形的相似比为2∶3，其中一个小三角形的最大边长为6，那么另一个三角形的最大边长为． 10．如图，地面上有一座古塔AB ，在离塔50米的点C 处，测得塔顶A 的仰角为α，测角仪CD 的高度为1.5米，那么此塔的高度AB 等于米（结果用含α的三角比表示）． 11．如图，已知⊙O 是△ABC 的内切圆，与AB 、AC 分别相切于点D 、E ，且BD =5，CE =6，那么BC = ． 12．在四边形ABCD 中，AD ∥BC ，AD ≠BC ，要使它成为等腰梯形，还需添加一个条件，这个条件可以是．二、选择题：（本大题共4题，满分16分）【下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的圆括号内，选对得4分；不选、错选或者多选得0分】13．化简23)2(x 所得的结果是……………………………………………………………（）（A ）52x ；（B ）54x ；（C ）62x ；（D ）64x ．14．一元二次方程032=-+a x ax 的根的情况是………………………………………（）（A ）有两个不相等的实数根；（B ）有两个相等的实数根；（C ）没有实数根；（D ）无法判断．15．如果两圆只有三条公切线，那么这两圆的的位置关系是…………………………（）（A ）内切；（B ）外切；（C ）相交；（D ）外离．16．下列命题中真命题是…………………………………………………………………（）（A ）两边分别对应相等且有一角为30º的两个等腰三角形全等；（B ）两边和其中一边的对角分别对应相等的两个三角形全等；（C ）两个锐角分别对应相等的两个直角三角形全等；（D ）两角和一边分别对应相等的两个三角形全等．C三、（本大题共5题，满分48分）17．（本题满分9分）计算：31108213)14.3(-⎪⎭⎫ ⎝⎛+-+--π．解：18．（本题满分9分）解方程组：⎩⎨⎧=+=-.54,522y x y x解：19．（本题满分10分）如图，已知菱形ABCD 的对角线AC 、BD 相交于点O ，AC =10，BD =24．求菱形的高AE ．解：20．（本题满分10分）如图，在Rt △ABC 中，已知∠ACB ＝90º，∠A ＝30º，BC =4．以点C 为旋转中心把△ABC 旋转到△C B A ''，点B 在边B A ''上，边C A '与边AB 相交于点D ．求△ABC 与△C B A ''重叠部分的面积．解：A B E D OA ' B21．（本题满分10分，第（1）、（2）小题各2分，第（3）、（4）小题各3分）某校640名学生参加了“爱我中华”作文竞赛．为了解这次作文竞赛的基本情况，从中随机抽取部分作文成绩汇总制成直方图（如右图），其中分数段与等第的关系如下表：（每组可含最（1）抽取的作文数量为篇；（2）抽取的作文中，80分及80分以上的作文数量所占的百分比是；（3）根据抽样情况估计，这次作文竞赛成绩的中位数落在等第组中；（4）估计参加作文竞赛的640名学生的作文成绩为A 等的人数约为名．四、（本大题共4题，满分50分）22．（本题满分12分，每小题各6分）已知：如图，在以点O 为圆心的两个同心圆中，大圆的半径OA 与小圆相交于点B ，AC 与小圆相切于点C ，OC 的延长线与大圆相交于点D ，AC 与BD 相交于点E ．求证：（1）BD 是小圆的切线；（2）CE ∶AE =OC ∶OD ．证明：23．（本题满分12分）A 、B 两地相距64千米，甲、乙两人分别从A 、B 两地骑车相向而行，且甲比乙晚出发40分钟．如果甲比乙骑车每小时多行4千米，那么两人恰好在AB 中点相遇．求甲、乙两人骑车的速度各是多少千米/小时．解：A ABCDE 等第24．（本题满分12分，第（1）小题2分，第（2）、（3）小题各5分）已知：二次函数k h x y +--=2)(图象的顶点P 在x 轴上，且它的图象经过点A （3，－1），与y 轴相交于点B ，一次函数b ax y +=的图象经过点P 和点A ，并与y 轴的正半轴相交．求：（1）k 的值；（2）这个一次函数的解析式；（3）∠PBA 的正弦值．解：25．（本题满分14分，第（1）、（2）小题各5分，第（3）小题4分）如图，已知等腰直角三角形ABC 中，∠C ＝90º，AC =2，M 是边AC 上一点，过点M 的直线交CB 的延长线于点N ，交边AB 于点P ，且AM =BN ．（1）求证：MP NP =；（2）设AM x =，四边形MCBP 的面积为y ，求y 与x 的函数解析式，并写出函数的定义域；（3）探索：以线段CM 为直径的圆能否与边AB 相切？如果能够相切，请求出x 的值；如果不能相切，请说明理由．（1）证明：（2）解：（3）解：N[参考答案]一、1．2； 2．x ≤3； 3．1≠x ； 4．（3，-4）； 5．111093.3⨯； 6．-2； 7．2； 8．0.7m ； 9．9； 10．1.5+50tg α； 11．11； 12．AB =DC 或AC =BD 或∠B =∠C 等．二、13．D ； 14．A ； 15．B ； 16．D ．三、17．解：原式=1+3+2-2………………………………………………（2分，2分，2分，2分） =4．……………………………………………………………………………（1分）18．解：由①得 52-=x y ③……………………………………………………………（1分）代入②得 5)5(22=-+x x ．……………………………………………………（1分）整理，得 01522=-+x x ．……………………………………………………（1分）解得 51-=x ，32=x ．…………………………………………………………（2分） ∴51-=y ，12-=y ．……………………………………………………………（2分）∴原方程组的解为⎩⎨⎧-=-=,5,511y x ⎩⎨⎧-==.1,322y x …………………………………………（2分） 19．解：在菱形ABCD 中， ∵AC =10，BD =24，∴521==AC CO ，1221==BD BO ．…………………（2分） ∵AC ⊥BD ，∴BC =13．…………………………………………………………（2分） ∵AE ⊥CD ，∴∠AEC =∠BOC =90°．…………………………………………（1分）∵∠ACE =∠BCO ，∴△AEC ∽△BOC ．………………………………………（2分） ∴BC AC BO AE =，即131012=AE ．……………………………………………………（1分） ∴13120=AE ．……………………………………………………………………（2分）（其他解法相应给分）20．解：∵∠ACB =90°，∠A =30°，∴∠ABC =60°．…………………………………（1分）又∵△ABC 绕点C 旋转到△C B A ''，且点B 在边B A ''上，∴4='=C B BC ，∠B '=∠ABC =60°．………………………………………（2分） ∴△BC B '为等边三角形．………………………………………………………（1分） ∴B BC '∠=60°．…………………………………………………………………（1分） ∵B C A ''∠=90°，∴∠BCD =30°．……………………………………………（1分） ∴∠BDC =90°．…………………………………………………………………（1分） ∴BD =2，32=CD ．……………………………………………………………（1分） ∴3232221=⨯⨯=BCD S ∆．…………………………………………………（2分） 21．解：（1）64；（2）37.5%；（3）C 组；（4）80名．……………（2分，2分，3分，3分）四、22．证明：（1）∵AC 与小圆O 相切于点C ，∴∠ACO =90º．…………………………（2分） ∵OD =OA ，OB =OC ，∠O =∠O ，∴△DOB ≌△AOC ．………………（1分）∴∠DBO =∠ACO =90º．…………………………………………………（1分）∵OB 是小圆的半径，∴BD 是小圆的切线．……………………………（2分）（2）∵△AOC ≌△DOB ，∴∠A =∠D ．………………………………………（1分）又∵∠EBA =∠DBO =90º，∴△ABE ∽△DBO ．………………………（1分）∴BE ∶AE =OB ∶OD ．……………………………………………………（1分）∵EB 、EC 与小圆分别相切于B 、C ，∴CE =BE ．……………………（2分）又∵OC =OB ，∴CE ∶AE =OC ∶OD ．……………………………………（1分）23．解：设乙骑车的速度是每小时x 千米，则甲骑车的速度是每小时（x +4）千米．（1分）根据题意，得604043232=+-x x ．…………………………………………………（5分）整理，得019242=-+x x ．……………………………………………………（2分）解得121=x ，162-=x ． ………………………………………………………（2分）经检验：121=x ，162-=x 都是原方程的解，但16-=x 不符合题意，舍去．∴原方程的解是12=x ．…………………………………………………………（1分）答：乙骑车的速度是每小时12千米，甲骑车的速度是每小时16千米．……（1分）24．解：（1）∵二次函数k h x y +--=2)(图象的顶点P 在x 轴上，∴k =0．………………………………………………………………………（2分）（2）∵二次函数2)(h x y --=的图象经过点A （3，-1），∴2)3(1h --=-．∴21=h ，42=h ．∴点P 的坐标为（2，0）或（4，0）． ……………………………………（1分）（i ）当点P 的坐标为（2，0）时，∵一次函数b ax y +=的图象经过点P 和点A ，∴⎩⎨⎧+=-+=.31,20b a b a 解得⎩⎨⎧=-=.2,1b a …………………………………………（1分）（ii ）当点P 的坐标为（4，0）时，∵一次函数b ax y +=的图象经过点P 和点A ，∴⎩⎨⎧+=-+=.31,40b a b a 解得⎩⎨⎧-==.4,1b a …………………………………………（1分） ∵一次函数的图象与y 轴的正半轴相交，∴⎩⎨⎧-==.4,1b a 不符合题意，舍去．……………………………………………（1分） ∴所求的一次函数解析式为2+-=x y ．…………………………………（1分）（3）∵点P 的坐标为（2，0），点A 的坐标为（3，-1），点B 的坐标为（0，-4）， ∴52=BP ，23=AB ，2=AP ．…………………………………（1分） ∴20)2()23(2222=+=+AP AB ，202=BP ．∴222BP AP AB =+．∴∠BAP =90°．……………………………………………………………（2分） ∴1010522sin ==∠PBA ．………………………………………………（2分） 25．（1）证明：过点M 作MQ ∥CN ，交AB 于点Q ．…………………………………（1分） ∵AC =BC ，∠C =90°，∴∠A =45°．∵MQ ∥CN ，∴∠AMQ =∠C =90°．∴∠AQM =∠A =45°．∴AM =MQ ．…………………………………………………………………（1分） ∵AM =BN ，∴MQ =BN ．……………………………………………………（1分）∵MQ ∥CN ，∴∠QMP =∠N ，∠MQP =∠NBP ．∴△MQP ≌△NBP ．…………………………………………………………（1分） ∴MP =NP ．…………………………………………………………………（1分）（2）过点P 作PD ⊥CN ，垂足为点D ．∴PD ∥AC ．∵MP =NP ，∴MC PD 21=．………………………………………………（1分） ∵AM =BN =x ，∴x MC -=2，)2(21x PD -=．…………………………（1分） ∴)2(2121)2)(2(21x x x x S S y BNP MNC -⋅--+=-=∆∆，………………（1分）即所求的函数解析式为221412+--=x x y ．……………………………（1分）定义域为0<x <2．……………………………………………………………（1分）（3）设以线段CM 为直径的圆的圆心为O ，过点O 作OF ⊥AB ，垂足为点F ．…………………………………………（1分） ∵121)2(21+=-+=x x x AO ，∠A =45°，∴)121(22+=x OF ．…（1分） ∵要使以线段CM 为直径的圆能与边AB 相切，必须有)2(2121x CM OF -==， ∴)2(21)121(22x x -=+．…………………………………………………（1分）解得246-=x ，即当246-=x 时，线段CM 为直径的圆能与边AB 相切．……………（1分）。

2006年中考专题-猜想、探索型专项训练及答案WORD

黄浦区初中毕业生学业考试数学模拟试卷一、填空题：(本题共12小题，每小题3分，满分36分） 1、－1的相反数的倒数是；2、=43)(x －____________；3、不等式)1(335+>-x x 的解集是______________；4、在实数范围内因式分解：=+232x x －_____________________；5、若x x 82=，则 x = ；6、函数81＋x y =的自变量x 的取值范围是____________________；7、若等边三角形的边长为a ，则它的面积为____________.；8、如果直线b x y +-=2在y 轴上的截距为－2，那么这条直线一定不经过第象限；9、已知a b ＝c d ＝e f ＝35 ，b ＋d ＋f ＝50，那么a ＋c ＋e ＝；10、正多边形的中心角是360，则这个正多边形的边数是；11、两圆内切，圆心距为3，一个圆的半径为5，另一个圆的半径为； 12、△ABC 是等腰直角三角形，BC 是斜边，将△ABP 绕点A 逆时针旋转后，能与△ACP ′重合。

如果AP=3，那么PP ′的长等于。

ABCP ′ P二、单项选择题：（本题共4小题，每小题4分，满分16分）【每题列出的四个答案中，只有一个是正确的，把正确答案的代号填入括号内】13、在Rt △ABC 中，∠C=90°，∠A 的对边为a ，已知∠A 和边a ，求边c ，则下列关系中正确的是( )(A) c=asinA ( B) c= a sinA (C) c=acosA (D) c= acosA14、在平面直角坐标中，点P （1，-3）关于x 轴的对称点坐标是：（A ）（1，-3）（B ）（-1，3）（C ）（-1，-3）（D ）（1，3）15、一批运动服按原价八五折出售，每套a 元，则它的原价为：（A ）0.85a 元（B ）a 1720元（C ）0.15a 元（D ）a 320元16、如图，A D ∥BC ,∠D=90°,DC=7,AD=2,BC=4.若在边DC 上有点P 使△PAD 和△PBC 相似，则这样的点P 存在的个数有（）(A) 1 ( B) 2 (C) 3 (D) 4三、简答题：（本题共5小题，第19、20题，每小题9分，第21、22、23题，每小题10分，满分48分）17、计算： 1212)31(201－）－（－-++-πD C BA18、用换元法解方程：xx x x 3121322-=--19、某区在5000名初三学生的数学测试成绩中，随机抽取了部分学生的成绩，经过整理后分成六组，绘制出的频率分布直方图（如图，图中还缺少90~100小组的小长方形），已知从左到右的第一至第五组的频率依次为0.05、0.1、0.3、0.25、0.2，第六小组的频数为25。

2006年上海数学试卷(文史类)答案

2006年上海数学试卷（文史类）试题及答案一、填空题：（4分⨯12=48分）1、已知集合{}1,3,A m =-，集合{}3,4B =。

若B A ⊆，则实数_____________m =解： {}4441,3,B A A B m A m ⊆⎫⎫⇒∈⎬⎪∈⇒=⎭⎬⎪=-⎭。

2、已知两条直线1:330l ax y +-=，2:4610l x y +-=。

若12//l l ，则__________a = 解：1233//2461a l l a -⇒=≠⇒=-。

3、若函数()(0,1)xf x a a a =>≠且的反函数的图象过点21-（，），则 __________a = 解：因为函数()(0,1)xf x a a a =>≠且的反函数的图象过点21-（，），所以函数()(0,1)xf x a a a =>≠且的图象过点2（-1,），即1122aa -=⇒=。

4、计算：23(1)lim__________61n n n n →∞+=+ 解：23222333111lim(1)(1)101lim lim lim 1161616066lim(6)n n n n n n n n n n n n n n n→∞→∞→∞→∞→∞+++++=====+++++。

5、若复数(2)(1)z m m i =-++为纯虚数（i 为虚数单位），其中m R ∈，则____________z = 解：复数(2)(1)z m m i =-++为纯虚数20210m m m -=⎧⇒⇒=⎨+≠⎩，代入已知，得333z i z i =⇒==。

6、函数sin cos y x x =的最小正周期是_______________________ 解：1sin cos sin 22y x x x ==，222T πππω===。

7、已知双曲线的中心在原点，一个顶点的坐标是(3,0)，且焦距与虚轴长之比为5:4，则双曲线的标准方程是____________________________解：由已知，所求双曲线的标准方程为22221x y a b -=。

2006年上海数学中考题

【只要求直接写出结果，每个空格填对得 3 分，否则得零分】
1．计算： 4 __________．
2．计算： 1 2 __________． xx
3．不等式 x 6 0 的解集是__________．
4．分解因式： x2 xy __________．__________． x3
Ｄ． x 1 x 1 x 1
14．二次函数 y x 12 3 图象的顶点坐标是（）
Ａ． 1，3
Ｂ． 1，3
Ｃ． 1， 3
Ｄ． 1， 3
15．在 △ABC 中， AD 是 BC 边上的中线， G 是重心．如果 AG 6 ，那么线段 DG 的长
为（）
Ａ． 2
Ｂ． 3
Ｃ． 6
Ｄ．12
16．在下列命题中，真命题是（）
10．已知在 △ABC 和 △A1B1C1 中， AB A1B1 ，∠A ∠A1 ，要使 △ABC ≌△A1B1C1 ，
还需添加一个条件，这个条件可以是__________．
11．已知圆 O 的半径为1，点 P 到圆心 O 的距离为 2 ，过点 P 引圆 O 的切线，那么切线长
是__________． 12．在中国的园林建筑中，很多建筑图形具有对称性．图 2 是一个破损花窗的图形，请把它补画成中心对称图形．
Ａ．两条对角线相等的四边形是矩形
Ｂ．两条对角线互相垂直的四边形是菱形
Ｃ．两条对角线互相平分的四边形是平行四边形
Ｄ．两条对角线互相垂直且相等的四边形是正方形
三．（本大题共 5 题，满分 48 分）
17．（本题满分 9 分）
先化简，再求值：
1
1 x
x2 1 x
，其中
x
2．
18．（本题满分 9 分）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2006年上海市初中毕业生统一学业考试数学试卷一．填空题：（本大题共12题，满分36分） 1=__________．2．计算：12x x+=__________．3．不等式60x ->的解集是__________． 4．分解因式：2x xy +=__________． 5．函数13y x =-的定义域是__________． 61=的根是__________．7．方程2340x x +-=的两个实数根为1x ，2x ，则12x x = __________．8．用换元法解方程2221221x x x x-+=-时，如果设221x y x =-，那么原方程可化为__________．9．某型号汽油的数量与相应金额的关系如图1所示，那么这种汽油的单价是每升__________元．10．已知在ABC △和111A B C △中，11AB A B =，1A A =∠∠，要使111ABC A B C △≌△，还需添加一个条件，这个条件可以是__________．11．已知圆O 的半径为1，点P 到圆心O 的距离为2，过点P 引圆O 的切线，那么切线长是__________． 12．在中国的园林建筑中，很多建筑图形具有对称性．图2是一个破损花窗的图形，请把它补画成中心对称图形．二．选择题：（本大题共4题，满分16分） 13．在下列方程中，有实数根的是（）Ａ．2310x x ++=1=- Ｃ．2230x x ++=Ｄ．111x x x =-- 14．二次函数()213y x =--+图象的顶点坐标是（）Ａ．()13-，Ｂ．()13，Ｃ．()13--，Ｄ．()13-，15．在ABC △中，AD 是BC 边上的中线，G 是重心．如果6AG =，那么线段DG 的长为（）Ａ．2Ｂ．3Ｃ．6Ｄ．12数量（单位：升）图1图216．在下列命题中，真命题是（）Ａ．两条对角线相等的四边形是矩形Ｂ．两条对角线互相垂直的四边形是菱形Ｃ．两条对角线互相平分的四边形是平行四边形Ｄ．两条对角线互相垂直且相等的四边形是正方形三．（本大题共5题，满分48分） 17．（本题满分9分）先化简，再求值：2111x x x -⎛⎫+÷ ⎪⎝⎭，其中x =18．（本题满分9分）解方程组：23010x y x y --=⎧⎨++=⎩，．19．（本题满分10分，每小题满分各5分）已知：如图3，在ABC △中，AD 是边BC 上的高，E 为边AC 的中点，14BC =，12AD =，4sin 5B =．求（1）线段DC 的长；（2）tg EDC ∠的值．AECDB 图320．（本题满分10分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分3分）某市在中心城区范围内，选取重点示范路口进行交通文明状况满意度调查，将调查结果的满意度分为：不满意、一般、较满意、满意和非常满意，依次以红、橙、黄、蓝、绿五色标识．今年五月发布的调查结果中，橙色与黄色标识路口数之和占被调查路口总数的15%．结合未画完整的图4中所示信息，回答下列问题：（1）此次被调查的路口总数是__________；（2）将图4中绿色标识部分补画完整，并标上相应的路口数；（3）此次被调查路口的满意度能否作为该市所有路口交通文明状况满意度的一个随机样本？答：____________________．21．（本题满分10分）本市新建的滴水湖是圆形人工湖．为测量该湖的半径，小杰和小丽沿湖边选取A ，B ，C 三根木柱，使得A ，B 之间的距离与A ，C 之间的距离相等，并测得BC 长为240米，A 到BC 的距离为5米，如图5所示．请你帮他们求出滴水湖的半径．红橙黄蓝绿标识图4图5四．（本大题共4题，满分50分）22．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图6，在直角坐标系中，O 为原点．点A 在第一象限，它的纵坐标是横坐标的3倍，反比例函数12y x=的图象经过点A ．（1）求点A 的坐标；（2）如果经过点A 的一次函数图象与y 轴的正半轴交于点B ，且OB AB =，求这个一次函数的解析式．23．（本题满分12分，每小题满分各6分）已知：如图7，在梯形ABCD 中，AD BC ∥，AB DC =．点E ，F ，G 分别在边AB ，BC ，CD 上，AE GF GC ==．（1）求证：四边形AEFG 是平行四边形；（2）当2FGC EFB =∠∠时，求证：四边形AEFG 是矩形．图6BE A DGC图7F24．（本题满分12分，第（1）小题满分5分，第（2）小题满分3分，第（3）小题满分4分）如图8，在直角坐标系中，O 为原点．点A 在x 轴的正半轴上，点B 在y 轴的正半轴上，tg 2OAB =∠．二次函数22y x mx =++的图象经过点A ，B ，顶点为D ．（1）求这个二次函数的解析式；（2）将OAB △绕点A 顺时针旋转90后，点B 落到点C 的位置．将上述二次函数图象沿y 轴向上或向下平移后经过点C ．请直接写出点C 的坐标和平移后所得图象的函数解析式；（3）设（2）中平移后所得二次函数图象与y 轴的交点为1B ，顶点为1D ．点P 在平移后的二次函数图象上，且满足1PBB △的面积是1PDD △面积的2倍，求点P 的坐标．25．（本题满分14分，第（1）小题满分4分，第（2）小题满分7分，第（3）小题满分3分）已知点P 在线段AB 上，点O 在线段AB 延长线上．以点O 为圆心，OP 为半径作圆，点C 是圆O 上的一点．（1）如图9，如果2AP PB =，PB BO =．求证：CAO BCO △∽△；（2）如果AP m =（m 是常数，且1m >），1BP =，OP 是OA ，OB 的比例中项．当点C 在圆O 上运动时，求:AC BC 的值（结果用含m 的式子表示）；（3）在（2）的条件下，讨论以BC 为半径的圆B 和以CA 为半径的圆C 的位置关系，并写出相应m 的取值范围．CA PB O图9数学试卷答案要点与评分标准一．填空题：（本大题共12题，满分36分） 1．2； 2．3x； 3．6x >；4．()x x y +；5．3x ≠；6．1；7．4-；8．2210y y -+=（或12y y+=）； 9．5.09；10．1B B =∠∠（或1C C =∠∠，或11AC AC =）； 1112．答案见图1．二．选择题：（本大题共4题，满分16分） 13．Ａ； 14．Ｂ； 15．Ｂ；16．Ｃ．三．（本大题共5题，满分48分）17．解：原式211x x x x+-=÷ ··························································································· （2分） ()()111x x x x x+-+=÷ ············································································· （2分） ()()111x xx x x +=+-················································································ （1分） 11x =-， ····································································································· （2分）当x =1==． ···························································· （2分） 18．解：消去y 得220x x +-=， ················································································· （3分）得12x =-，21x =， ························································································· （3分）由12x =-，得15y =-， ·················································································· （1分）由21x =，得22y =-， ···················································································· （1分） ∴原方程组的解是1125x y =-⎧⎨=-⎩，；2212x y =⎧⎨=-⎩，． ·························································· （1分） 19．解：（1）在Rt BDA △中，90BDA =∠，12AD =，4sin 5AD B AB ==， ·· （1分） 15AB ∴=． ··········································································································· （1分）图1229B D ∴=． ························································ （2分） 1495DC B C BD ∴=-=-=． ········································································ （1分）（2）［方法一］过点E 作EF DC ⊥，垂足为F ，EF AD ∴∥． ············· （1分）A E E C =，1522DF DC ∴==，162EF AD ==． ·································· （2分） ∴在Rt EFD △中，90EFD =∠，12tg 5EF EDC DF ==∠． ······················· （2分）［方法二］在Rt ADC △中，90ADC =∠，12tg 5AD C DC ==． ················ （2分） DE 是斜边AC 上的中线，12DE AC EC ∴==． ······································· （1分）E D C C ∴=∠∠． ································································································ （1分）12tg tg 5EDC C ∴==∠． ··················································································· （1分）20．（1）60； ·················································································································· （3分）（2）图略（条形图正确，得2分；标出数字10，得2分）； ······························ （4分）（3）不能． ··················································································································· （3分） 21．解：设圆心为点O ，连结OB ，OA ，OA 交线段BC 于点D ． ························ （1分）AB AC = ， AB AC ∴=．OA BC ∴⊥，且11202BD DC BC ===．······························································································································· （1分）由题意，5DA =． ····························································································· （1分）在Rt BDO △中，222OB OD BD =+， ························································· （2分）设OB x =米， ···································································································· （1分）则()2225120x x =-+， ··················································································· （2分）1442.5x ∴=． ··································································································· （1分）答：滴水湖的半径为1442.5米． ····································································· （1分）四．（本大题共4题，满分50分）22．解：（1）由题意，设点A 的坐标为()3a a ，，0a >． ········································· （1分）点A 在反比例函数12y x =的图象上，得123a a=， ······································ （1分）解得12a =，22a =-， ························································································ （1分）经检验12a =，22a =-是原方程的根，但22a =-不符合题意，舍去． ······ （1分） ∴点A 的坐标为()26，． ······················································································· （1分）（2）由题意，设点B 的坐标为()0m ，． ·························································· （1分）0m > ，m ∴= ···································································· （2分）解得103m =，经检验103m =是原方程的根，∴点B 的坐标为1003⎛⎫⎪⎝⎭，． ···· （1分）设一次函数的解析式为103y kx =+， ································································· （1分）由于这个一次函数图象过点()26A ，，10623k ∴=+，得43k =． ················ （1分） ∴所求一次函数的解析式为41033y x =+． ······················································· （1分）23．证明：（1）在梯形ABCD 中，AB DC =，B C ∴=∠∠． ························ （2分）G F G C = ，C GFC ∴=∠∠． ······································································ （1分）B G FC ∴=∠∠，AB GF ∴∥，即AE GF ∥． ··········································· （1分） A E G F = ，∴四边形AEFG 是平行四边形． ··············································· （2分）（2）过点G 作GH FC ⊥，垂足为H ． ·························································· （1分）G F G C = ，12FGH FGC ∴=∠∠． ···························································· （1分）2F G C E F B = ∠∠，FGH EFB ∴=∠∠． ················································· （1分）90FGH GFH +=∠∠，90EFB GFH ∴+=∠∠． ······························ （1分） 90EFG ∴=∠． ·································································································· （1分）四边形AEFG 是平行四边形，∴四边形AEFG 是矩形． ··························· （1分） 24．解：（1）由题意，点B 的坐标为()02，， ······························································ （1分） 2OB ∴=，tg 2OAB = ∠，即2OBOA=． 1OA ∴=．∴点A 的坐标为()10，． ···································································· （2分）又二次函数22y x mx =++的图象过点A ，2012m ∴=++．解得3m =-， ········································································································· （1分） ∴所求二次函数的解析式为232y x x =-+． ··················································· （1分）（2）由题意，可得点C 的坐标为()31，， ··························································· （2分）所求二次函数解析式为231y x x =-+． ···························································· （1分）（3）由（2），经过平移后所得图象是原二次函数图象向下平移1个单位后所得的图象，那么对称轴直线32x =不变，且111BB DD ==． ····················································································· （1分）点P 在平移后所得二次函数图象上，设点P 的坐标为()231x x x -+，．在1PBB △和1PDD △中，112PBB PDD S S = △△，∴边1BB 上的高是边1DD 上的高的2倍．①当点P 在对称轴的右侧时，322x x ⎛⎫=-⎪⎝⎭，得3x =，∴点P 的坐标为()31，；。