带通滤波器传递函数
一种具备高镜像抑制比的带通滤波器设计

一种具备高镜像抑制比的带通滤波器设计王海兵【摘要】介绍一种高镜像抑制比的带通滤波器的设计。
在音频领域里所接触的大多为实数滤波器,滤波器的频率点具备对称性的特点,这就对信号处理领域带来很大的麻烦,如AM、FM中频滤波时产生的镜像频率,会对正常的搜台产生很大的干扰。
此设计利用复数滤波器的特点,设计出一种具备高镜像抑制比的带通滤波器,应用于数字调谐收音机解调系统里面。
由于采用的是全集成的复数带通滤波器,节省了传统的外部中频滤波器的成本及空间;实测镜像抑制比达40 dB,大大降低了搜台的误操作,提高了整机系统的信噪比,在信号处理领域有一定的借鉴意义。
%The paper introduces a design of bandpass filter with high image rejection ratio. In the audio field, we contact mostly real filter, this filter have the characteristics of symmetry, which will bring the field of signal processing to a lot of trouble, such as the mirror frequency to produce AM, FM intermediate frequency filtering, will have a lot of interference to the channel search normal, this design uses the characteristics of complex filter, design a rejectio n bandpass filters with high image rejection ratio, it’s used in digital tuning radio demodulation system, due to the use of the fully integrated bandpass filter, saves cost and space outside of the traditional intermediate frequency filter; inhibition ratio of 40 dB image rejection, greatly reduces the error operation channel search, improves the signal-to-noise ratio of the system, has certain reference meanings to the field of signal processing.【期刊名称】《电子与封装》【年(卷),期】2014(000)010【总页数】4页(P16-19)【关键词】复数域带通滤波器;抑制镜像;信号处理【作者】王海兵【作者单位】无锡市晶源微电子有限公司,江苏无锡 214028【正文语种】中文【中图分类】TN402在现代电子接收机中,如手机、收音机等,内含的低中频放大器需抑制镜像频率信号[1]。
带通滤波器传递函数

带通滤波器传递函数
带通滤波器传递函数是处理信号的一个重要部分,它主要用于给定滤波器决定信号特性,以及滤波器性能。
因此,了解滤波器传递函数及其机理,对于弄清滤波器的行为及其性能有着非常重要的意义。
一般来说,带通滤波器传递函数由滤波器的类型、形状及其他参数决定。
它表示了信号从滤波器的输入端到输出端之间的变化,主要受到滤波器的类型、形状及其他参数的影响。
带通滤波器可以分类为直流带通滤波器、低通滤波器、高通滤波器、带阻滤波器、全通滤波器、低和高通滤波器、带阻和全通滤波器、孤对称滤波器等几类。
各类滤波器的传递函数各不相同,而且是非线性的,因此,在表示它们的传递函数时要根据具体实例来选择描述方式。
带通滤波器传递函数的表示方法主要有传统的频谱表示和结构
算子表示两种。
传统的频谱表示方法是通过表示出频谱来描述滤波器的传递函数,它可以描述滤波器输出对输入的响应情况,即从频率的角度描述滤波器的传递函数。
结构算子表示是通过表示出结构算子来描述滤波器的传递函数,它允许我们从时间域的角度去描述滤波器的传递函数。
带通滤波器传递函数的绘制一般是在滤波器的设计阶段进行的,它有助于我们理解滤波器的行为,而且可以帮助我们判断滤波器的性能,以便能够更加准确地去设计符合要求的滤波器。
此外,带通滤波器传递函数还可以帮助我们判断滤波器是否存在失真。
总之,带通滤波器传递函数是评价滤波器性能的重要方法,也是
对滤波器行为的有效描述,用于设计滤波器也是十分有用的。
因此,了解并选择合适的表示方法,可以帮助我们更加准确地设计和操作滤波器,更有效地处理信号。
二阶带通滤波器 传递函数

二阶带通滤波器传递函数
二阶带通滤波器是一种可以通过某一特定范围内的频率信号,同时抑制其他频率信号的滤波器。
它的传递函数可以表示为:
$H(s)=\frac{s^2+ω_0^2}{s^2+\frac{ω_0}{Q}s+ω_0^2}$
其中,$ω_0$是中心频率,$Q$是品质因数。
品质因数$Q$决定了带通滤波器的通带宽度和阻带宽度之间的比例。
较高的品质因数会导致更窄的带通和更陡峭的阻带,但也会增加滤波器的群延迟。
传递函数中的零点将产生频率上升响应,而极点将产生频率下降响应。
二阶带通滤波器的设计需要综合考虑其传递函数和实际需求,以满足特定的应用场景。
二阶带通滤波器中心频率和固有频率

《深入理解二阶带通滤波器:中心频率和固有频率的探讨》在探讨二阶带通滤波器的中心频率和固有频率之前,让我们先了解二阶带通滤波器的基本原理和应用。
二阶带通滤波器是一种常见的电子滤波器,它可以通过选择适当的电路元件和参数来实现对特定频率范围内信号的增强,并对其他频率的信号进行抑制。
在讨论中心频率和固有频率之前,我们需要先了解滤波器中的一些基础知识。
1. 二阶带通滤波器的基本原理二阶带通滤波器是由一个高通滤波器和一个低通滤波器级联构成的。
它的传递函数可以表示为:H(s) = k * (s^2) / (s^2 + (s/Q) + 1)其中,s是复频域变量,k是系统增益,Q是品质因数。
二阶带通滤波器可以在选择合适的参数后实现对特定频率范围内信号的增强,是一种非常常用的滤波器。
2. 中心频率的概念中心频率是指带通滤波器增益最大的频率点,也是滤波器响应曲线的中心位置。
在二阶带通滤波器中,中心频率通常由下式计算得出:fc = 1 / (2 * π * √(L * C))其中,fc表示中心频率,L表示电感值,C表示电容值。
中心频率决定了滤波器对特定频率范围内信号的响应程度,是设计带通滤波器时需要考虑的重要参数。
3. 固有频率的意义固有频率是指带通滤波器自身的振荡频率,也是在没有外部输入信号作用时,滤波器自由振荡的频率。
在二阶带通滤波器中,固有频率可以用下式表示:f0 = 1 / (2 * π * √(L * C))与中心频率类似,固有频率也与电感值和电容值有关。
固有频率可以反映出滤波器自身的特性,是分析滤波器稳定性和振荡特性的重要参数。
4. 理论与实际应用在实际应用中,中心频率和固有频率是设计二阶带通滤波器时需要重点考虑的参数。
通过合理选择电感值和电容值,可以实现对特定频率范围内信号的增强,同时保持滤波器的稳定性和响应速度。
在设计滤波器时,需要根据实际需求去调整中心频率和固有频率,以实现最佳的滤波效果。
总结回顾通过以上的讨论,我们对二阶带通滤波器的中心频率和固有频率有了更深入的了解。
四种滤波器的幅频特性教程文件

四种滤波器的幅频特性四种滤波器的幅频特性本次实验是观察四种滤波器(低通、高通、带宽、带阻)的幅频特性,以加强对各种滤波器的功能认知。
本次实验我们选用的放大器为324型,其功能图如下所示:下面我们来逐步观察一下四种滤波器的特性。
1.低通滤波器其电路图如下所示:图中,电阻R1=R2=R=10KΩ,C1=C2=0.01uF,Ro=0.8R=8Ω,Vcc+=+12V,Vcc-=-12V ,低通滤波器的传递函数20022)(ωαωω++=s s K s H p ,,其中2221102121001111;1;1C R K R R C C C R R RRK K ff p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数据w 。
=10000rad/s ,Kp =1.8,α=1.2,()()222202225/2425/78.1)(ωωωωω+-=j H ;当w =0时)(ωj H =1.8,;w 增加且w<4800rad/s 时,)(ωj H 增加;当>4800rad/s 时, )(ωj H 减小,;w 趋近无穷时, )(ωj H 趋近于0。
此时wc=1.17rad/s 。
对于不同的α,滤波器的幅频特性也不相同对于实验中的低通,α=1.2,与1.25的相似,我们对于实验数据的测量如下:输入为100mV 频率f (Hz )输出V (v ) 频率f (Hz ) 输出V (v ) 10 1.965 2200 0.756 30 1.965 2300 0.698 50 1.960 2400 0.650 100 1.950 2500 0.596 2001.94526000.548500 1.945 2700 0.518 800 1.945 2800 0.484 1000 1.855 2900 0.438 1100 1.795 3000 0.414 1200 1.755 3500 0.311 1300 1.700 4000 0.238 1400 1.490 4500 0.180 1500 1.400 5000 0.148 1600 1.290 5500 0.123 1700 1.195 6000 0.105 1800 1.095 7000 0.078 1900 0.966 8000 0.057 2000 0.898 9000 0.046 2100 0.818 10000 0.036 范围10~6kHz输出不失真绘出的幅频特性图如下:2、高通滤波器其电路图如下:其中R1=R2=R=10K,C1=C2=0.01uF,Ro=0.8R=8K高通的传递函数为2022)(ωαω++=s s s K s H p ,()()222022)(ωαωωωωω+-=p K j H ,1121202121001111;1;1CR K C C R C C R R RR K K f f p -+⎪⎪⎭⎫ ⎝⎛+==+==αωω带入数值后,Kp =1.8,W=0时)(ωj H =0;w<4800rad/s 时)(ωj H 增加;w 趋近于无穷时, )(ωj H 保持不变。
表41二阶滤波器的标准传递函数.
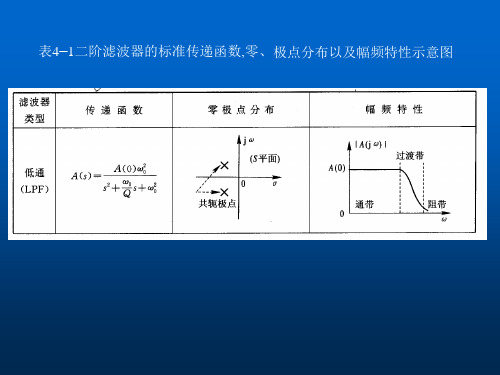
(4—35)
0
(4—36)
画出幅频特性如图 4—25(b) 所示。调节 R2, 使中心频 率变化,但带宽不变,增益也不变。这是该电路的特 点,也是优点,如图4—25(c)所示。
R1 ui
C4 C3
R5 - A + Rp (a )
R2
uo
图4—25带通滤波器
| A(jω) | A(ω0 ) 0 .7 07 A(ω0 )
LPH
HPF
uo
BW
1 1 1 若令Y1 ,Y2 ,Y3 sC3 , Y4 sC4 , Y5 R1 R2 R5
则该电路为带通滤波器,如图3—25(a)所示。令
C3=C4=C,其传递函数为 1 s CR1 Auf ( s ) 2 R R2 s2 s 21 CR5 C R1R2 R5
4.3.2 二阶压控电压源高通滤波电路
频率特性: u+ uo
式中:
要求:Aup﹤3
其幅频特性曲线如图:
运放作为无限增益放大器的多重反馈有源滤波器
Y1 ui C Y2
Y4 Y3 B Rp
Y5 - A + uo
多重反馈有源滤波器
4.3.3 带通滤波电路BPF
BPF作用是使某频段内的有 用信号通过,而高于或低于 此频段的信号将被衰减。
| A(jω) | R2
0
ω0 (b )
BW =
ω0 Q
ω
0
ω0 1
ω0 2 (c)
ω0 3
ω
图4—25 (a)电路;(b)幅频特性;(c)调节R2,幅频特性移动
4.3.4 带阻滤波电路(BEF)
作用是阻止某一频段内 为中心频率 的信号通过, 达到抗干扰 的目的,又名陷波器。 特性曲线是:
运放传递函数

运放传递函数
运放的传递函数是表示运放输入信号和输出信号之间关系的公式。
它
可以用来描述运放的放大倍数和相位关系。
运放传递函数的形式取决于具
体的运放电路和工作方式。
以下是几种常见的运放传递函数:
1.理想放大器传递函数。
在理想情况下,运放被视为一个理想放大器,没有任何偏置电流、输
入电压漂移和噪声等问题。
其传递函数可以表示为:
A(s)=Vo/Vi。
2.非反馈运放传递函数。
非反馈运放是一种基于差动放大器的电路,它的传递函数可以表示为:A(s) = (Rf/R1) * (1 + jw*CF*R2)。
其中,Rf和R1是反馈电阻和输入电阻,CF是放大器的频率响应补偿
电容,R2是差动放大器的负载电阻。
3.反馈运放传递函数。
反馈运放是一种通过反馈电路修正放大器增益的电路。
其传递函数可
以表示为:
A(s)=(1+Rf/R1)/(1+Rf/R2)。
其中,Rf是反馈电阻,R1和R2是放大器输入电阻和输出电阻。
4.带通滤波器传递函数。
带通滤波器是一种常用的电路,用于选择一定范围内的频率信号。
其传递函数可以表示为:
H(s)=(R2/R1)*(sL/R2+1)/(sC+sL+R1/R2)。
其中,L和C是滤波器的电感和电容,R1和R2是滤波器输入和输出电阻。
总之,不同类型的运放电路和应用场景都有各自的传递函数,需要根据具体情况进行选择和使用。
RC滤波原理简介

RC 无源滤波器电路及其原理
在测试系统中,常用RC 滤波器。
因为在这一领域中,信号频率相对来说不高。
而RC 滤波器电路简单,抗干扰性强,有较好的低频性能,并且选用标准的阻容元件易得,所以在工程测试的领域中最经常用到的滤波器是RC 滤波器。
1)一阶RC 低通滤波器
RC 低通滤波器的电路及其幅频、相频特性如下图所示。
设滤波器的输入电压为ex 输出电压为ey ,电路的微分方程为:
这是一个典型的一阶系统。
令 τ=RC ,称为时间常数,对上式取拉氏变换,有:
H y y x
y
x sE E E E E τ+=令(s )= H(s)是传递函数
或
其幅频、相频特性公式为:
分析可知,当f很小时,A(f)=1,信号不受衰减的通过;当f很大时,A(f)=0,信号完全被阻挡,不能通过。
2)一阶RC高通滤波器
RC高通滤波器的电路及其幅频、相频特性如下图所示。
设滤波器的输入电压为ex输出电压为ey,电路的微分方程为:
同理,令=RC,对上式取拉氏变换,有:
或
其幅频、相频特性公式为:
分析可知,当f很小时,A(f)=0,信号完全被阻挡,不能通过;当f很大时,A(f)=1信号不受衰减的通过. 3)RC带通滤波器
带通滤波器可以看作为低通滤波器和高通滤波器的串联,其电路及其幅频、相频特性如下图所示。
其幅频、相频特性公式为:H(s) = H1(s) * H2(s)
式中H1(s)为高通滤波器的传递函数,H2(s)为低通滤波器的传递函数。
有:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
带通滤波器传递函数
带通滤波器传递函数是滤波器的重要性能指标,反映滤波器在不同频率下的能量传递情况。
一般用以下公式表示:
H(s)=H(jω)=A(jω) / A(0)
如果是一阶高通滤波器,它的特性方程一般表示如下:
H(s)= τ / (τ + s)
其中τ为滤波器的时间常数,s为变量,表示频率的负绝对值。
当频率ω时,可以把变量s取得调整为―−(jω)的形式:
传递函数在有限频率范围内,通常把它表示为一阶低通滤波器的传递函数,即一阶高通滤波器的负转置,这样做通常用到阿贝尔型滤波器。
一阶高通型滤波器的传递函数H(s)如下所示:
当频率ω时,变量s取得调整为―jω,于是传递函数可表示为:
滤波器衰减通常是用滤波器传递函数的模量和相位来表示的。
模量和相位可以用函数处理的方法导出,如下:
{| 模量| H(jω) |
| -- | -- |
| 20 对数模量 | 10log(|H(jω)|^2) |
| 相位 | arg(H(jω)) |
带通滤波器传递函数能够反映出该滤波器在不同频率下响应的过程,从而给出高效滤波器的设计参数。
此外,从传递函数中可以得到滤波器的带宽等特性,有助于更加精确的设计和更好的应用。
