神经网络建模
人工神经网络建模(Artificial Neuron Nets)
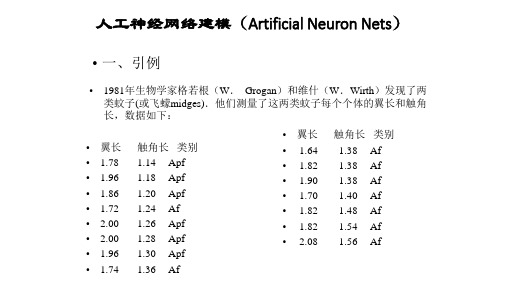
• 一、引例
• 1981年生物学家格若根(W. Grogan)和维什(W.Wirth)发现了两 类蚊子(或飞蠓midges).他们测量了这两类蚊子每个个体的翼长和触角 长,数据如下: • • • • • • • • • 翼长 1.78 1.96 1.86 1.72 2.00 2.00 1.96 1.74 触角长 类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
m
例如,若记
z wi xi
i 1
m
ቤተ መጻሕፍቲ ባይዱ
• 取激发函数为符号函数
1, x 0, sgn( x) 0, x 0.
则
1, y f ( z) 0,
• S型激发函数:
w x w x
i 1 i i 1 m i
m
i
, ,
i
1 f ( x) , x 1 e
• 规 定 目 标 为 : 当 t(1)=0.9 时 表 示 属 于 Apf 类 , t(2)=0.1表示属于Af类。 • 设两个权重系数矩阵为:
w1 (1,1) w1 (1,2) w1 (1,3) W1 w1 (2,1) w1 (2,2) w1 (2,3)
( p) l
( p1) l
(i, j) a ( j),
( p) ( p) l l 1
l 1,...,L,
(10)
w (i, j )
表示第-1层第个元对第层第个元输入 的第次迭代时的权重
( p) l
其中
( p) L
大脑神经网络连接建模

大脑神经网络连接建模大脑是人类最神秘、最复杂的器官之一,其中神经网络的表现和功能一直是研究人员关注的焦点。
大脑神经网络连接建模是一种通过模拟大脑神经元之间的连接、传递和处理信息的过程,来解析大脑认知活动的方法。
大脑是由上百亿个神经元组成的,它们之间通过神经突触进行信息传递。
通过建立神经网络连接模型,研究者可以更好地理解大脑的工作原理,揭示认知和行为的基本机制。
神经网络连接建模的关键是建立神经元之间连接的拓扑结构。
大脑的神经网络是高度复杂、互连的,可以分为多个脑区和亚区,每个区域都有不同的功能和特性。
因此,研究者需要根据不同脑区的特点来构建连接模型,以便更好地模拟大脑的整体工作过程。
在建模过程中,研究者通常通过采集大脑的结构和功能数据来获取连接信息。
结构数据包括脑区的解剖特征、体积和形状等,而功能数据则反映了大脑在特定任务下的活动模式。
这些数据可以通过核磁共振成像(MRI)和脑电图(EEG)等技术获取。
建立连接模型后,研究者需要进行大脑功能网络的分析和探索。
他们可以使用图论、复杂网络理论和机器学习等方法,来研究神经网络的拓扑结构、节点之间的关联和信号传递等特征。
通过这些分析方法,研究者可以揭示大脑网络的特性,如小世界结构、高度聚集性和无标度网络特性等。
此外,大脑神经网络连接建模还可用于探索大脑疾病的机制和治疗方法。
例如,研究者可以对比正常大脑和病理大脑的连接模型,发现病理性变化的特征和变化。
这有助于理解疾病的发病机制,并为相关疾病的诊断和治疗提供依据。
除了理论模型外,研究者还可以利用计算机模拟来研究大脑神经网络的连接和功能。
计算机模拟可以模拟大脑中的庞大神经网络,通过调整不同的参数和拓扑结构,来探索不同条件下神经网络的行为和功能。
总之,大脑神经网络连接建模是研究者解析大脑认知机制的重要手段。
通过构建神经网络的连接模型,分析网络的拓扑结构和功能特征,研究者可以更好地理解大脑的工作原理和机制。
这项研究对于认知科学、神经科学和临床医学都具有重要意义,有望为人类认知和大脑疾病的研究提供新的思路和方法。
大脑神经网络建模及其功能意义

大脑神经网络建模及其功能意义简介:人类大脑是一个复杂且神秘的器官,其中神经元通过复杂的网络连接和相互作用,构成了一个庞大的神经网络系统。
大脑神经网络建模是研究人脑结构和功能的重要手段之一。
通过模拟和探索神经网络的构建和工作原理,我们可以更好地理解大脑在认知、感知、学习等方面的功能意义。
一、大脑神经网络建模方法1. 静态建模静态建模是一种将大脑神经网络表示为静态连接模式的方法。
这种方法可以通过扫描和图像处理技术,将大脑的结构和连接关系转化为图像或网络拓扑图。
静态建模的优点是简单易懂,可以提供有关大脑区域之间连接性的信息。
然而,它无法揭示大脑的动态特性和信息传递过程。
2. 动态建模动态建模是一种模拟大脑神经网络活动的方法。
通过建立数学模型、仿真计算等手段,可以模拟大脑神经元之间的相互作用和信息传递过程。
这种方法可以更加真实地模拟和理解大脑的动态功能。
然而,由于大脑神经网络的复杂性,动态建模需要大量的计算资源和高级的算法支持。
二、大脑神经网络建模的功能意义1. 深入理解大脑运作机制大脑神经网络建模可以帮助我们深入理解大脑的运作机制。
通过模拟和分析神经网络的动态特性,可以揭示神经元之间的相互影响和信息传递过程。
这有助于我们更好地理解大脑在认知、感知、学习等方面的机制和原理。
2. 解释认知功能与行为大脑神经网络建模还可以帮助我们解释人类的认知功能和行为。
通过与实际观测和实验结果进行比对,我们可以验证和验证神经网络模型的准确性和可靠性。
这有助于我们探索和理解认知功能与行为的本质。
3. 治疗神经系统疾病大脑神经网络建模对于治疗神经系统疾病也具有重要意义。
通过建立神经网络模型,我们可以模拟疾病对大脑神经网络的影响,从而更好地理解并设计相关的治疗方法。
这为神经系统疾病的治疗和康复提供了重要的依据和指导。
4. 辅助人工智能设计大脑神经网络建模还可以为人工智能的设计和开发提供有益的启示。
人脑作为高度智能的系统,具有强大的信息处理能力。
人工神经网络建模matlab

四、反向传播算法(B-P算法)
• Back propagation algorithm
• 算法的目的:根据实际的输入与输出数据, 计算模型的参数(权系数)
• 1.简单网络的B-P算法
u (i) • (2) 设 k
表示第k层第i神经元所接收的信息
wk(i,j) 表示从第k-1层第j个元到第k层第i个元的权重,
ak (i) 表第k层第i个元的输出
• (3)设层与层间的神经元都有信息交换(否则, 可设它们之间的权重为零);但同一层的神经元 之间无信息传输.
• (4) 设信息传输的方向是从输入层到输出层方向; 因此称为前向网络.没有反向传播信息.
• 分类结果:(1.24,1.80),(1.28,1.84)属 于Af类;(1.40,2.04)属于 Apf类.
图2 分类直线图
• •缺陷:根据什么原则确定分类直线?
• 若取A=(1.46,2.10), B=(1.1,1.6)不变,则分类直线 变为 y=1.39x+0.071
分类结果变为: (1.24,1.80), (1.40,2.04) 属于Apf类; (1.28,1.84)属于Af类
• 问:如果抓到三只新的蚊子,它们的触角长和翼长 分别为(l.24,1.80); (l.28,1.84);(1.40,2.04).问 它们应分别属于哪一个种类?
• 解法一:
• 把翼长作纵坐标,触角长作横坐标;那么 每个蚊子的翼长和触角决定了坐标平面的一个 点.其中 6个蚊子属于 APf类;用黑点“·”表示; 9个蚊子属 Af类;用小圆圈“。”表示.
神经网络的建模与仿真

神经网络的建模与仿真随着科技的发展,越来越多的研究人员开始将神经网络应用于各个领域,如医疗、金融、自然语言处理等。
神经网络作为现代人工智能技术的核心,其建模与仿真技术也越来越受到关注。
神经网络的建模可以分为两个部分:架构的设计和权值的学习。
架构的设计通常使用基于数据的方法和基于先验知识的方法,其中基于数据的方法采用启发式搜索等技术自动寻找最优结构,而基于先验知识的方法则根据领域知识构建结构。
常见的神经网络架构包括前馈神经网络、循环神经网络、卷积神经网络等。
权值的学习是指通过训练数据来确定神经网络中各个神经元之间的权值,以最小化目标函数。
常见的训练算法包括梯度下降法、反向传播算法等。
仿真是评估神经网络模型性能的重要手段,通过对模型进行仿真可以了解模型在不同条件下的行为,从而优化模型的性能。
仿真工具包括MATLAB、Python等。
在使用这些工具时,需要注意对仿真过程中的各个参数进行控制,以确保仿真结果的准确性和稳定性。
在实际应用中,神经网络经常被用作分类器或回归器。
分类器用于将输入数据归类到不同的类别中,而回归器则用于估计输入数据与输出数据之间的映射关系。
除了分类器和回归器,神经网络还可以用于聚类、降维等任务,如自编码器和深度信念网络。
神经网络的成功应用离不开数据的支撑。
建模和仿真需要大量的数据来支持,数据的准确性和多样性对神经网络的表现影响极大。
因此,在应用神经网络时,需要注意对数据集的选择和预处理,以确保数据质量和可靠性。
总之,神经网络作为现代人工智能的核心技术,在各个领域都有着广泛应用。
神经网络建模和仿真技术的发展为神经网络应用提供了坚实的基础,相信在不久的将来,神经网络将在更广阔的领域内发挥更大的作用。
大脑神经网络建模与认知功能理解

大脑神经网络建模与认知功能理解人类的大脑是一个复杂而精巧的系统,通过神经网络的建模可以帮助我们更好地理解大脑的认知功能。
本文将探讨大脑神经网络的建模方法以及如何通过这些模型来理解我们的认知功能。
大脑由不同的脑区组成,每个脑区都有不同的功能和结构。
神经网络建模的目的是模拟这些脑区之间的连接和交互方式。
研究人员可以使用电生理学记录、神经成像和计算模型等方法来构建这些神经网络模型。
其中,计算模型特别重要,它可以帮助我们创造虚拟的神经网络,以便进行更深入的研究和实验。
在大脑神经网络建模中,最有影响力的模型之一是神经元网络模型。
这个模型基于对神经元多边形结构和功能的研究。
神经元是神经网络的基本单位,它们通过突触相互连接,通过电信号传递信息。
神经元网络模型模拟了这种结构和功能,并使用数学方程描述神经元之间的相互作用。
通过这个模型,研究人员可以研究神经元之间的信号传递、突触可塑性、神经网络的动态行为等等。
大脑神经网络建模还包括大规模连接模型,它模拟了大脑的整体连接方式。
这些模型使用复杂的数学算法和计算机模拟来模拟数十亿个神经元之间的连接。
这些模型可以帮助我们理解大脑在认知任务中的高层次处理机制。
例如,在面部识别任务中,大规模连接模型可以模拟大脑的视觉系统,从而帮助我们理解大脑如何处理和识别不同的面部特征。
通过大脑神经网络建模,我们可以更好地理解大脑的认知功能。
认知功能包括感知、注意、记忆、学习和决策等过程。
通过建立神经网络模型,研究人员可以了解不同脑区在这些认知过程中的作用和相互关系。
例如,注意力是一个重要的认知功能,它允许我们集中注意力在感兴趣的事物上。
神经网络模型可以帮助我们理解大脑如何选择和调控注意力资源,并解释一些注意力障碍的原因。
此外,通过神经网络建模,我们还可以研究大脑的学习和记忆过程。
大脑通过神经元之间的突触可塑性来存储和检索信息。
神经网络模型可以帮助我们理解这种突触可塑性的机制,并解释不同类型的记忆和学习障碍。
神经网络计算-建模讲义解析

去生成80个训练样本、25个检测样本进行实验。训练样本 精度达到95%左右,而检验样本精度在65-80%之间.
-
71
作业
设计一个 BP 网络对上图中的英文字母进行分类。输入 向量含1 2 个分量,输出单元个数取1,分别用-1、0和1代 表字符A、I、O。训练时可选择不同的隐节点数及不同的 学习率进行对比。
-
60
活化函数 • Sigmoid函数
gx 1
1exp(x) -
fxtanh(x)
61
双曲正切函数
• 表达式:
tanh(x)
eexx
ex ex
.
• 图像
-
62
Sigmoid函数特点
• 光滑, 单调递增,上、下有界(称为饱和性). • 导数值可由其函数值给出
gx 1- g(x) g(x);
模式识别、函数逼近和数据压缩等问题。
返回
-
8
人工神经网络的结构
具有一个隐层的前馈网络 单层全连接反馈网络
-
9
神经网络的特性
• 鲁棒性(容错) • 并行计算 • 自我学习 • 硬件实现 • 求满意解
-
10
神经网络的三要素
• 网络结构; • 信息流动规则; • 权值学习规则。
-
11
神经网络的学习方式
输入样本向量预处理
• 输入样本向量的各个分量有时在数量级上
差异较大,若不进行适当的处理,数量级 大的分量可能完全湮没其它分量的作用。 为此在训练开始之前,需对各个分量做相 应的调整,使其具有大致相同的数量级。
-
59
输入样本向量预处理
人体神经网络系统建模及功能解析分析

人体神经网络系统建模及功能解析分析人体的神经网络系统是一个复杂而精密的组织,由大脑、脊髓和周围神经组成。
它具有多种功能,包括感知、运动控制、内脏活动的调节以及思维和意识的产生。
本文将对人体神经网络系统的建模和功能进行解析分析。
首先,人体的神经网络系统可以通过建模来理解其结构和功能。
建模的目标是对整个系统进行抽象和描述,以便更好地研究和理解其运行机制。
建模可以基于不同层次和尺度的方法,包括分子、细胞、组织和器官水平。
例如,分子层面的建模可以研究神经递质在突触传递中的作用,细胞层面的建模可以研究神经元的电活动和兴奋性传导,组织层面的建模可以研究不同脑区之间的连接和信息传递,器官层面的建模可以研究大脑和脊髓在整体行为和认知中的作用。
其次,神经网络系统的功能可以通过分析其组成部分的相互作用来进行解析。
神经元是神经网络系统的基本单位,它们之间通过突触连接形成复杂的网络。
神经元的兴奋性传导和突触传递是神经网络系统功能实现的关键。
神经元的兴奋性传导是指当神经元受到足够的刺激时,电信号会沿着它的轴突传导到突触,并通过神经递质释放到下一个神经元。
突触传递是指神经递质在突触间隙中传递,以影响下一个神经元的兴奋性状态。
这些传导和传递过程的细节和效率对于神经网络系统的功能实现至关重要。
神经网络系统的功能还可通过研究特定区域和结构的功能分化来进行解析。
大脑是神经网络系统的核心,负责高级认知功能、意识、思维和情感调节。
大脑有多个区域和结构,每个区域和结构都有特定的功能。
例如,脑干控制基本的生命维持功能,大脑皮层负责感知和运动控制,海马体负责记忆和学习等。
通过研究这些区域和结构的功能分化,可以更深入地了解神经网络系统的整体功能。
此外,神经网络系统的功能可以通过研究其在疾病状态下的改变来进行解析。
神经网络系统在多种神经系统疾病中发挥关键作用,如阿尔茨海默病、帕金森病和精神分裂症等。
通过比较疾病和健康状态下神经网络系统的差异,可以揭示疾病的发病机制和病理过程,为疾病的诊断和治疗提供理论基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3、网络结构以及工作方式
从连接方式看NN主要有两种网络拓扑结构: 前馈型网络:结点分为输入单元和计算单元 反馈型网络:所有结点都是计算单元 NN的工作过程主要分为两个阶段: 第一阶段:学习期,此时个计算单元状态不变,各 连线上的权值可通过学习来修改 第二阶段:工作期,此时各连接权值固定,计算各 单元状态变化
1, x 0 1, x 0 1、阶跃函数:f ( x) ,或符号函数f ( x) 0, x 0 1, x 0 e x e x 2、双曲正切函数:f ( x) tanh( x) x x e e x2 ,x 0 3、sigmoid函数(S型):f ( x) 1 x 2 0, x 0 1 n 4、高斯函数:f ( x) exp 2 ( x j x ji )2 2 i i 1
1.5数据结构:影响网络仿真的输入数据结构的格式
静态网络中的同步输入仿真:
例1
动态网络中的异步输入仿真:当网络中存在延迟时,顺序发 生的输入向量就要按一定的序列输入网络。为了演示这种情 况,我们以一个有延迟的简单网络为例。
动态网络中的同步输入仿真
如果我们在上例中把输入作为同步而不是异步应用, 我们就会得到完全不同的响应。这就好象每一个输入 都同时加到一个单独的并行网络中。在前一个例子中, 如果我们用一组同步输入,我们有: p1=[1], p2=[2],p3=[3], p4=[4] 这可用下列代码创建: P =[1 2 3 4]; 模拟这个网络,我们得到: A = sim(net,P) A= 1234
在某些特定的情况下,我们可能想要在同一时间模拟一些不同序 列的网络响应。这种情况我们就要给网络输入一组同步序列。比 如说,我们要把下面两个序列输入网络: p(1)=[1], p(2)=[2],p(3)=[3], p(4)=[4] p(1)=[4], p(2)=[3],p(3)=[2], p(4)=[1] 输入 P应该是一个细胞数组,每一个数组元素都包含了两个同时发生 的序列的元素。 P = {[1 4] [2 3] [3 2] [4 1]}; 现在我们就可以模拟这个网络了: A = sim(net,P); 网络输出结果将是: A = {[ 1 4] [4 11] [7 8] [10 5]} 可以看到,每个矩阵的第一列是由第一组输入序列产生的输出序 列,每个矩阵的第二列是由第二组输入序列产生的输出序列。这 两组序列之间没有关联,好象他们是同时应用在单个的并行网络 上的。
1.1、人工神经元模型
人工神经网络的基本单元的神经元模型
人工神经元的三个要素
1、一组连接(突触),连接强度由各连接上的权值wij 表示,权值为正表 示激活,负表示抑制 2、一个求和单元 ,用于求取各输入信号之间的加权和 wij xi
i 1 m
3、一个非线性激活函数f,起到非线性映射的作用并将神经元的输出限制 在一定范围内 还有阈值 j (或偏置b j j ), 可通过把输入维数增加一维把阈值包括进去 y j f ( wij xi ), (i 0对应阈值 j,w0 j =1或偏置w0 j = 1)
网络结构:前馈型神经网络
两个或更多的上面所示的神经元可以组合成一层,一个典 型的网络可包括一层或者多层。我们首先来研究神经元层。 单层神经元网络 有R输入元素和S个神经元组成的单层网络如下图所示
n{1}=net.IW{1,1}*p+net.b{1}
多层神经元网络
上面所示的网络有R1个输入,第一层有S1个神经元,第二层 有S2个神经元…
i 0 m
1.2激活(传递)函数的取法
在Matlab工具箱里包括了许多激活(传递)函数。在 “Transfer Function Graphs”中可以找到它们的完全 列表 函数名 功 能 purelin 线性传递函数 hardlim 硬限幅递函数 hardlims 对称硬限幅递函数 satli 饱和线性传递函数 satlins 对称饱和线性传递函数 logsig 对数S 形传递函数 tansig 正切S 形传递函数 radbas 径向基传递函数 compet 竞争层传递函数
注意:我们把第三层的输出a3标记为y。我们将使用这种符号
来定义这种网络的输出。
1.4创建网络
newp newlind newlin newff newcf newfftd newrb newrbe newgrnn newpnn newc newsom newhop newelm 创建感知器网络 设计一线性层 创建一线性层 创建一前馈 BP 网络 创建一多层前馈 BP 网络 创建一前馈输入延迟 BP 网络 设计一径向基网络 设计一严格的径向基网络 设计一广义回归神经网络 设计一概率神经网络 创建一竞争层 创建一自组织特征映射 创建一 Hopfield 递归网络 创建一 Elman 递归网络
1、神经网络简介
人工神经网络是在现代神经科学的基础上发展起来的, 旨在模拟人脑结构以及功能的一种抽象的数学模型,其 中Hopfield神经网络、ART神经网络、BP神经网络是常 用的网络。 •Hopfield神经网络是由相同的神经元构成的单元,是一 类不具有学习能力的单层自联想网络,她的网络模型由 一组可使某一个能量函数最小的微分方程组成。 •ART神经网络主要用于模式识别,她的不足之处在于 对转换、失真和规模变化较敏感 •BP神经网络是误差反向传播的多层前向网络,其信息处 理机制由神经元激活特性和网络拓扑结构决定,神经元 的传递函数是非线性函数,网络结构由输入层、隐含层、 输出层组成,同层节点间无关联 ,异层节点前向连接。
ห้องสมุดไป่ตู้
中间层的输出就是下一层的输入。第二层可看作有S1个输入, S2个神经元和S1xS2 阶权重矩阵W2 的单层网络。第二层的输 入是a1,输出是a2,现在我们已经确定了第二层的所有向量 和矩阵,我们就能把它看成一个单层网络了。其他层也可以 照此步骤处理。
多层网络的功能非常强大。例、一个两层的网络,第一层的 转移函数是曲线函数,第二层的转移函数是线性函数,通过 训练,它能够很好的模拟任何有有限断点的函数。这种两层 网络集中应用于“反向传播网络”。
