2016年秋季学期新版沪教版七年级数学上册4.4角(1)素材
【课件】七年级上册数学第4章4.4角沪科版-(共32张PPT)

例1 判断正误,对的打“√”,错的打“×”. (1)有公共端点的两条射线叫做角.( × ) (2)两条射线组成的图形叫做角.( × ) (3)角的大小与角画出的两边的长短无关.( √ ) (4)由一条射线绕一点旋转而形成的图形叫做 角.( × )
导引:紧扣角的两种定义来进行判断.
总结
判断角的方法: 静态定义的条件:①两条射线;②有公共端点; ③组成的图形. 动态定义的条件:①一条射线;②绕它的端点旋 转;③形成的图形. 本例中,(1)没有“组成的图形”,而“两条射线”是 角的边;(2)缺少“公共端点”;(4)应该是“绕它的 端点”旋转.
第4章 直线与角
4.4 角
1 课堂讲解 2 课时流程
角及有关角的定义 角的表示方法 角的度量 方向角
逐点 导讲练
课堂 小结
作业 提升
知识点 1 角及有关角的定义
钟面上的时针与分针所构成的图形、四面体中任意两条 相交棱所构成的图形(图4 - 21 ),都给我们以角的形象.
图4 - 21
定义:(1)角的静态定义:从一点出发的两条射线 组成的图形叫做角.这个点叫做角的顶点,这两条 射线是角的两条边. (2)角的动态定义:由一条射线绕着它的端点旋转 而形成的图形叫做角.
例3 如图,写出符合以下条件的角: (1)能用一个大写字母表示的角; (2)以A为顶点的角; (3)小于平角的角.
导引:用一个大写字母表示的角不能有其他角与它共 用顶点.
解:(1)∠B,∠C. (2)∠BAC,∠BAD,∠CAD. (3)∠BAC,∠B,∠C,∠1,∠2,∠3,∠4.
总结
1.表示角时,若用一个大写字母表示某角,则该角不能 有其他角与它共用顶点,如图中∠BAD,∠BAC, ∠CAD,∠BDA,∠CDA都不能用一个大写字母表示, 以免混淆.
沪科版-数学-七年级上册-七年级数学上册第四章:4.4角的度量与表示素材

课堂引入案例
案例1
现在是几点钟?这时,时针与分针组成了什么图形?
角。
角的大小与时针的长短有关吗?
没有关系。
怎样用我们学过的几何概念来定义角?比如用点、线段、射线、直线等。
由两条射线组成,并且两条射线有一个公共的端点,这样的图形叫做角。
这个公共的端点叫做角的顶点;这两条射线叫做角的边。
角的两边应该是射线,但画时根据需要画就可以。
一个三角形的角,在放大镜下看时,角度变大吗?
没有变大。
角的大小与角两边的长短无关
案例2
观察下面的图形,你发现什么共同的特点吗?
这些图形都给了我们角的形象.
角可以看成是由一条射线绕着它的端点旋转而成的图形.起始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
角有以下几种表示方法
如果终边继续旋转,可以有两种特殊情况:第一种情况是绕着端点旋转到角的终边和始边成一直线,这时所成的角叫做平角;第二种情况是绕着端点旋转到终边和始边重合,这时所成的角叫做周角.。
沪科版七年级数学上册4.4 角 课件

感悟新知
知识点 2 角的表示方法
角的几何符号为“∠”,角的表示方法有以下几种
表示方法 示例
用三个大写 字母表示
记法
∠ AOB 或 ∠ BOA
方法解读
字母O 表示顶点, 要写在中间,A,B 表示角的两边上的 点,用该表示法可 以表示任何一个角
感悟新知
表示方法 示例 用一个大写 字母表示
用数字表示 用希腊字母 表示
(2)10
°6
′36
″=10
°+6
′+36
″=10
°+6
′+36×
(
1 60
)
′=
10°+6 ′+0.6 ′=10 °+6.6 ′=10 °+6.6×( 1 ) °=10 °+0.11 °=
60
10.11°
感悟新知
例4 计算: (1)27°26′+53°48′; (2)90°-79°18′6″; (3)18°13′×5; (4)49°28′52″÷4.
②角的大小与所画边的长短有关;
③角的两边可以画得一样长,也可以一长一短;
④角的两边是两条射线;
⑤因为平角的两边成一条直线,所以一条直线可以看成一个平角;
⑥周角是一条射线. 其中,正确说法的个数为( )
A. 2
B. 3
C. 4
D. 5
学习目标
解题秘方:紧扣角的定义中的关键词进行辨析.
特别提醒 判断角要按定义中的关键词进行识别.“静”态要扣住:顶 点、两边这些要素;“动”态要紧扣射线的始边、终边 这些要素. 角的大小与所画边的长短无关,因为角的两边是射线, 不可以度量.角的大小只与构成角的两边张开的大小有关. 角既可以度量,也可以比较大小,还可以参与运算.
沪科版七年级上册 数学 课件 4.4 角 (1)

1、判断:下面的图形哪些是角?
⑴
⑵
⑶
⑷
⑸
⑹
不是
是 不是
是 不是
是
2、指出下面角的内部和外部
外部 内部 在没有特别说明的情况下,我 们说的角都是在0°-180°之间。
角的概念(二)
B
O
A
角 二:
通过刚才的演示, 你能否再给角一个定义呢?
角的概念(二)
角也可以看成是一条射线绕着它的端点旋转 而成的图形。
谢谢
谁来做一做
4、写出图中能用一个字母表示的角
( ∠A 和∠C
)
(2)以B为顶点的角 ( ∠ABE、∠EBC、 ∠ABC )
5. 如图所示: (1) 图中共有多少个角?请写出能用一个字
母表示的角;
答案:8个;∠A,∠O.
(2) 把图中所有的角都表示出来.
A
答案:∠A,∠O,∠1,
∠2,∠3,∠4,
∠ABC,∠ACB.
4.4 角
小荷才露尖尖角, 早有蜻蜓立上头。
房 顶 的角
吊 扇 扇 叶 的 夹 角
剪刀的角
人 仰 视 时 的 视 角
楼梯的折角
时针和分针的夹角
角 4.4
通过上面对
角的认识,你能 用自己的话对角 作一个描述吗?
角的概念(一) B 边
顶点O
边
A
角是由有公共端点的两条射线所组成的
图形。
这个公共端点叫做这个角的顶点 这两条射线叫做这个角的边
起始位置的射线叫做这个角的始边
。 终止位置的射线叫做这个角的终边
。
终边 B
o 始边 A
B
O
A
如果一个角的终边继续旋转,旋转到与始 边成一条直线时,所成的角叫做平角。
沪科版-数学-七年级上册-第四章:4.4角的度量与表示素材1
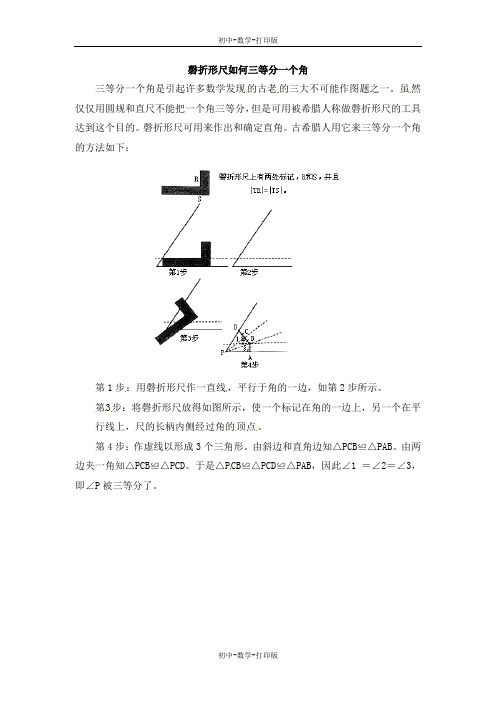
磬折形尺如何三等分一个角
三等分一个角是引起许多数学发现的古老的三大不可能作图题之一。
虽然仅仅用圆规和直尺不能把一个角三等分,但是可用被希腊人称做磬折形尺的工具达到这个目的。
磬折形尺可用来作出和确定直角。
古希腊人用它来三等分一个角的方法如下:
第1步:用磬折形尺作一直线,平行于角的一边,如第2步所示。
第3步:将磬折形尺放得如图所示,使一个标记在角的一边上,另一个在平行线上,尺的长柄内侧经过角的顶点。
第4步:作虚线以形成3个三角形。
由斜边和直角边知△PCB≌△PAB。
由两边夹一角知△PCB≌△PCD。
于是△PCB≌△PCD≌△PAB,因此∠1 =∠2=∠3,即∠P被三等分了。
七年级数学上册 第4章4.4 角例题与讲解 (新版)沪科版

4.4 角1.角的有关概念(1)钟面上的时针与分针所构成的图形、四面体中任意两条相交棱所构成的图形,都给我们以角的形象.(2)角可以看作是从一点O出发的两条射线OA,OB所组成的图形.如图,其中,点O 叫做角的顶点,射线OA,OB叫做角的边.这个角可记作∠AOB,读作“角AOB”.∠AOB也可以看成是射线OA绕着点O旋转到OB的位置后形成的图形.射线OA,OB分别叫做这个角的始边和终边.(3)当角的终边是由始边旋转半周得到的(这时角的始边和终边互为反向延长线),如图,这样的角叫做平角,1平角=180°.(4)当角的终边是由始边旋转一周得到的(这时角的始边和终边重合成一条射线,但它不是一条射线),如图,这样的角叫做周角,一周角=360°.释疑点理解角的特征(1)角有两个特征:一是角有两条射线,二是角的两条射线必须有公共端点,二者缺一不可;(2)由于射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边的长短无关;(3)当角的大小一旦确定,它的大小不会因为图形的位置、图形的放大或缩小而改变;(4)平角与直线有区别,平角是一个角,它有角的内部,而直线是一条线,这是两个不同的概念,不能说“一条直线就是平角”或“平角是一条直线”,同样不能说“一条射线是周角”;(5)没有特别说明,本书中所指的角都是指小于平角的角.【例1】下列说法:①两条射线所组成的图形叫做角;②一条射线旋转而成的图形叫做角;③角的大小与这个角的两边长短有关;④平角是一条直线.其中错误的有( ).A.1个B.2个C.3个D.4个①×没有说明两条射线是否有公共端点,缺少组成的要素,所以①错误.②×没有说明两条射线是否有公共端点,缺少组成的要素,所以②错误.③×角的两边都是射线,因此角的大小与这个角的两边长短无关,所以③错误.④×平角和一条直线的图形是一样的,但平角和直线是两个不同的概念,所以不能说平角是一条直线,所以④错误.释疑点概念是识别图形的依据角的概念是识别一个图形是否是角的主要依据,其他图形的识别也是如此,所以我们要十分重视对概念的正确理解.2.角的表示方法(1)用三个大写字母表示:如图,角的顶点为O,角的两边为射线OA,OB,该角可记为:∠AOB或∠BOA(顶点的大写字母写在中间).(2)用一个大写字母表示:当以某一点为顶点的角只有一个时,可用表示这个点的字母表示这个角,如上图,这个角又可表示为∠O.(3)用数字表示:如下图中的两个角,我们可以表示为∠1和∠2,同时在原图中,需要在顶点数加上弧线.(4)用希腊字母表示:如下图中的两个角,我们可以表示为∠α和∠β,同时在原图中,需要在顶点处加上弧线.释疑点如何准确地表示角当以某个字母为顶点的角仅有一个时,才能用表示其顶点的一个大写字母来表示该角.用阿拉伯数字或小写的希腊字母表示角时,一定要在图中该角的位置上标出字母或数字,并画上弧线.【例2】如图,下列表示∠1的方法中,正确的是( ).A.∠A B.∠ABCC.∠BAD D.∠BAC解析:根据角的四种表示方法的规定,只有∠BAC与∠1表示同一个角,因此应选D.答案:D3.角的度量(1)角的度量单位:角的度量单位是度、分、秒.度、分、秒之间的进率是60.(2)把一个周角平均分成360等份,每一份就是1度的角,1度记作1°;把1°的角60等分,每一份是1分的角,1分记作1′;把1′的角60等分,每一份是1秒的角,1秒记作1″.这种以度、分、秒为单位的角的度量制,叫做角度制.(3)角度的换算:1°=60′,1′=60″.由以上关系式可将度化为度、分、秒的形式,也可将度、分、秒化成度的形式.析规律正确进行角的换算用度、分、秒表示度时,要先把度的小数部分化成分,再把分的小数部分化成秒;用度表示度、分、秒时,要先把秒化成分,再把分化成秒;遇到乘法时,先乘再进位,遇到加法时,先加再进位,遇到减法时,先借位再减.【例3】解答下列问题:(1)用度、分、秒表示57.53°;(2)用度表示36°23′45″;(3)计算53°25′28″×5;(4)已知∠α=32.68°,∠β=18°41′55″,求∠α-∠β.解:(1)57.53°=57°+0.53×60′=57°+31.8′=57°+31′+0.8×60″=57°+31′+48″ =57°31′48″;(2)因为45″=⎝ ⎛⎭⎪⎫4560′=0.75′, 23.75′=⎝ ⎛⎭⎪⎫23.7560°≈0.396°, 所以36°23′45″≈36.396°;(3)53°25′28″×5=265°125′140″=267°7′20″;(4)因为∠α=32.68°=32°40′48″,所以∠α-∠β=32°40′48″-18°41′55″=32°39′108″-18°41′55″=31°99′108″-18°41′55″=13°58′53″.析规律 角的加减乘除运算进行角的加减乘除运算,遇到加法时,先加再进位;遇到减法时,先借位再减;遇到乘法时,先乘再进位;遇到除法时,先借位再除.4.探索角的个数探索由一个点引出若干条射线组成的角的个数时,可按边分别按逆时针或顺时针的顺序数,先确定以一条边为始边的所有角的个数,再确定以另一条边为始边的所有角的个数,以此类推,再求和可得角的总个数,并利用这一关系求出从一个点出发若干条射线时构成的角的个数的规律.数角时,观察一定要有条理,既要防止重复,又要防止遗漏.解技巧 从一个顶点出发的n 条射线组成的角的个数一般地,从点O 出发引出n 条射线,能组成(n -1)个基本角,共有角的个数为(n -1)+(n -2)+…+3+2+1=n (n -1)2. 【例4】 观察下列图形,并阅读相关文字:从图中的规律能知道从一个点出发10条射线时构成__________个不同的角.解析:2条射线构成角的个数为1;3条射线构成角的个数为2+1=3;4条射线构成角的个数为3+2+1=6;5条射线构成角的个数为4+3+2+1=10;…;由此可得10条射线构成角的个数为9+8+7+6+5+4+3+2+1=45.答案:455.钟表盘上角的度量与换算钟表上的时针与分针如果看作两条射线,不同时刻它们组成的角大小不同,时针与分针不同时间分别旋转过的角的大小各不相同,解决这类问题的关键是判断不同时刻时针与分针的位置以及各自每分钟旋转的角度的大小,然后运用角的定义和度量解决问题.【例5】 若时针由2点30分走到2点55分,问时针、分针各转过多大角度?分析:时针和分针每分钟转过的角度如下表所示.时针 一小时转一小格 一小时转30° 一分钟转0.5°分针 一小时转一圈 一小时转360° 一分钟转6° 解:所以分针转过的角度为360°60×(55-30)=6°×25=150°, 时针转过的角度为360°60×12×(55-30)=150°×112=12.5°.6.实际问题中的方位角的操作方位角一般以正北、正南为基准,描述物体所在的方向.如图所示的是我们常用到的一些方向,但实际上八个方向还不够用,如果要详尽准确地表示每一个方向上的角,就要借助角度来表示.(1)用射线表示的方位角一般说法是北偏东×度,北偏西×度,南偏东×度,南偏西×度.一般把南、北放在前,但东南、西南、西北、东北例外.(2)方位角是表示方向的射线与正北、正南方向的夹角,若已知条件给的不是这个角度,则需转化成与正北、正南方向的夹角.(3)通常规定上北、下南、左西、右东.【例6】 如图,在一张某地区的地图上,原标有学校、公园和广场三个位置,由于被墨水污染,广场的具体位置已看不清了.根据记忆,广场位置在学校的北偏东60°的方向,在公园的北偏西45°的方向.根据上述信息,请找出广场的具体位置.分析:根据题意,可知广场在学校的北偏东60°的方向.画图时,应以学校所在地为测点,在此处画出上北下南,左西右东的方向,以正北方向的射线为始边,顺时针旋转60°,则广场的位置就在这条射线上,同理,在公园的位置作一条北偏西45°的射线,这两条射线的交点,即为广场的位置.解:所画的图形如图所示.。
七年级数学上册 第4章4.4 角例题与讲解 (新版)沪科版
4.4 角1.角的有关概念(1)钟面上的时针与分针所构成的图形、四面体中任意两条相交棱所构成的图形,都给我们以角的形象.(2)角可以看作是从一点O出发的两条射线OA,OB所组成的图形.如图,其中,点O 叫做角的顶点,射线OA,OB叫做角的边.这个角可记作∠AOB,读作“角AOB”.∠AOB也可以看成是射线OA绕着点O旋转到OB的位置后形成的图形.射线OA,OB分别叫做这个角的始边和终边.(3)当角的终边是由始边旋转半周得到的(这时角的始边和终边互为反向延长线),如图,这样的角叫做平角,1平角=180°.(4)当角的终边是由始边旋转一周得到的(这时角的始边和终边重合成一条射线,但它不是一条射线),如图,这样的角叫做周角,一周角=360°.释疑点理解角的特征(1)角有两个特征:一是角有两条射线,二是角的两条射线必须有公共端点,二者缺一不可;(2)由于射线是向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它的边的长短无关;(3)当角的大小一旦确定,它的大小不会因为图形的位置、图形的放大或缩小而改变;(4)平角与直线有区别,平角是一个角,它有角的内部,而直线是一条线,这是两个不同的概念,不能说“一条直线就是平角”或“平角是一条直线”,同样不能说“一条射线是周角”;(5)没有特别说明,本书中所指的角都是指小于平角的角.【例1】下列说法:①两条射线所组成的图形叫做角;②一条射线旋转而成的图形叫做角;③角的大小与这个角的两边长短有关;④平角是一条直线.其中错误的有( ).A.1个B.2个C.3个D.4个①×没有说明两条射线是否有公共端点,缺少组成的要素,所以①错误.②×没有说明两条射线是否有公共端点,缺少组成的要素,所以②错误.③×角的两边都是射线,因此角的大小与这个角的两边长短无关,所以③错误.④×平角和一条直线的图形是一样的,但平角和直线是两个不同的概念,所以不能说平角是一条直线,所以④错误.释疑点概念是识别图形的依据角的概念是识别一个图形是否是角的主要依据,其他图形的识别也是如此,所以我们要十分重视对概念的正确理解.2.角的表示方法(1)用三个大写字母表示:如图,角的顶点为O,角的两边为射线OA,OB,该角可记为:∠AOB或∠BOA(顶点的大写字母写在中间).(2)用一个大写字母表示:当以某一点为顶点的角只有一个时,可用表示这个点的字母表示这个角,如上图,这个角又可表示为∠O.(3)用数字表示:如下图中的两个角,我们可以表示为∠1和∠2,同时在原图中,需要在顶点数加上弧线.(4)用希腊字母表示:如下图中的两个角,我们可以表示为∠α和∠β,同时在原图中,需要在顶点处加上弧线.释疑点如何准确地表示角当以某个字母为顶点的角仅有一个时,才能用表示其顶点的一个大写字母来表示该角.用阿拉伯数字或小写的希腊字母表示角时,一定要在图中该角的位置上标出字母或数字,并画上弧线.【例2】如图,下列表示∠1的方法中,正确的是( ).A.∠A B.∠ABCC.∠BAD D.∠BAC解析:根据角的四种表示方法的规定,只有∠BAC与∠1表示同一个角,因此应选D.答案:D3.角的度量(1)角的度量单位:角的度量单位是度、分、秒.度、分、秒之间的进率是60.(2)把一个周角平均分成360等份,每一份就是1度的角,1度记作1°;把1°的角60等分,每一份是1分的角,1分记作1′;把1′的角60等分,每一份是1秒的角,1秒记作1″.这种以度、分、秒为单位的角的度量制,叫做角度制.(3)角度的换算:1°=60′,1′=60″.由以上关系式可将度化为度、分、秒的形式,也可将度、分、秒化成度的形式.析规律正确进行角的换算用度、分、秒表示度时,要先把度的小数部分化成分,再把分的小数部分化成秒;用度表示度、分、秒时,要先把秒化成分,再把分化成秒;遇到乘法时,先乘再进位,遇到加法时,先加再进位,遇到减法时,先借位再减.【例3】解答下列问题:(1)用度、分、秒表示57.53°;(2)用度表示36°23′45″;(3)计算53°25′28″×5;(4)已知∠α=32.68°,∠β=18°41′55″,求∠α-∠β.解:(1)57.53°=57°+0.53×60′=57°+31.8′=57°+31′+0.8×60″=57°+31′+48″=57°31′48″;(2)因为45″=⎝ ⎛⎭⎪⎫4560′=0.75′, 23.75′=⎝ ⎛⎭⎪⎫23.7560°≈0.396°, 所以36°23′45″≈36.396°;(3)53°25′28″×5=265°125′140″=267°7′20″;(4)因为∠α=32.68°=32°40′48″,所以∠α-∠β=32°40′48″-18°41′55″=32°39′108″-18°41′55″=31°99′108″-18°41′55″=13°58′53″.析规律 角的加减乘除运算进行角的加减乘除运算,遇到加法时,先加再进位;遇到减法时,先借位再减;遇到乘法时,先乘再进位;遇到除法时,先借位再除.4.探索角的个数探索由一个点引出若干条射线组成的角的个数时,可按边分别按逆时针或顺时针的顺序数,先确定以一条边为始边的所有角的个数,再确定以另一条边为始边的所有角的个数,以此类推,再求和可得角的总个数,并利用这一关系求出从一个点出发若干条射线时构成的角的个数的规律.数角时,观察一定要有条理,既要防止重复,又要防止遗漏.解技巧 从一个顶点出发的n 条射线组成的角的个数一般地,从点O 出发引出n 条射线,能组成(n -1)个基本角,共有角的个数为(n -1)+(n -2)+…+3+2+1=n (n -1)2. 【例4】 观察下列图形,并阅读相关文字:从图中的规律能知道从一个点出发10条射线时构成__________个不同的角.解析:2条射线构成角的个数为1;3条射线构成角的个数为2+1=3;4条射线构成角的个数为3+2+1=6;5条射线构成角的个数为4+3+2+1=10;…;由此可得10条射线构成角的个数为9+8+7+6+5+4+3+2+1=45.答案:455.钟表盘上角的度量与换算钟表上的时针与分针如果看作两条射线,不同时刻它们组成的角大小不同,时针与分针不同时间分别旋转过的角的大小各不相同,解决这类问题的关键是判断不同时刻时针与分针的位置以及各自每分钟旋转的角度的大小,然后运用角的定义和度量解决问题.【例5】 若时针由2点30分走到2点55分,问时针、分针各转过多大角度?分析:时针和分针每分钟转过的角度如下表所示.时针 一小时转一小格 一小时转30° 一分钟转0.5°分针 一小时转一圈 一小时转360° 一分钟转6° 解:所以分针转过的角度为360°60×(55-30)=6°×25=150°, 时针转过的角度为360°60×12×(55-30)=150°×112=12.5°.6.实际问题中的方位角的操作方位角一般以正北、正南为基准,描述物体所在的方向.如图所示的是我们常用到的一些方向,但实际上八个方向还不够用,如果要详尽准确地表示每一个方向上的角,就要借助角度来表示.(1)用射线表示的方位角一般说法是北偏东×度,北偏西×度,南偏东×度,南偏西×度.一般把南、北放在前,但东南、西南、西北、东北例外.(2)方位角是表示方向的射线与正北、正南方向的夹角,若已知条件给的不是这个角度,则需转化成与正北、正南方向的夹角.(3)通常规定上北、下南、左西、右东.【例6】 如图,在一张某地区的地图上,原标有学校、公园和广场三个位置,由于被墨水污染,广场的具体位置已看不清了.根据记忆,广场位置在学校的北偏东60°的方向,在公园的北偏西45°的方向.根据上述信息,请找出广场的具体位置.分析:根据题意,可知广场在学校的北偏东60°的方向.画图时,应以学校所在地为测点,在此处画出上北下南,左西右东的方向,以正北方向的射线为始边,顺时针旋转60°,则广场的位置就在这条射线上,同理,在公园的位置作一条北偏西45°的射线,这两条射线的交点,即为广场的位置.解:所画的图形如图所示.。
新沪科版七年级上册数学教学课件 第4章 几何图形初步 4.4 角 第1课时 角的定义及表示方法
_∠__C__O_D__.
DC B
O
A
2. 填表:
直角
α
α
【教材P154 练习 第2题】
平角
α
α
α
0°<α< 90°
90°<α< 180°
α=180°
随堂练习
1.如图,下列说法正确的是( D )
A.∠1与∠AOC表示同一个角
C
B.∠AOC也可以用∠О表示
βB
C.∠β表示的是∠AOC
O1
A
D.图中共有三个角,分别是∠AOB,
第4章 几何图形初步 4.4 角
第1课时 角的定义 及表示方法
分针所构成的图形、四面体 中任意两条相交棱所构成的图形,都呈现了什么 样的形象?
钟面上的时针与分针所构成的图形、 四面体中任意两条相交棱所构成的图形, 都呈现了角的形象.
新知探究
角的表示方法:
知识点2 角的分类
B
O
A (B)
当射线OA 绕点О旋转,第一次旋转到与OA在同一 条直线上时,形成的角叫作平角.
继续旋转回到初始位置OA时,形成的角叫作周角.
角的分类:
角度范围
角的名称
相互关系
0°<∠α<90° ∠α=90°
90°<∠α<180° ∠α=180° ∠α=360°
锐角 直角 钝角 平角 周角
D
AO
B
课堂小结
角的表示方法:
角的分类:
①三个大写英文字母; 0°<∠α<90° 锐角
②一个大写字母;
∠α=90°
直角
③阿拉伯数字;
90°<∠α<180° 钝角
④希腊字母.
∠α=180°
平角
∠α=360°
4.4角 第一课时 课件 沪科版 数学七年级上册
角也可以看做一条射线绕端点旋转所组 成的图形。
终边
· 顶点
角的内部。
始边
角的定义二: 一条射线绕着它的端点从一个位置旋转到另一个位置所形
成的图形称为角。射线旋转时经过的平面部分叫角的内部。
角的表示:
角用符号“∠”来表示.
方法一:
∠ BOC能记作
∠O吗?为什么 ?
用三个大写字母:用三个大写字母 表示时,中间字母是顶点字母;角 的边各取一个字母写在两旁
3、用一个数字 4、希腊字母表示
4.平角、周角的概念
注意事项 表示顶点的字母要写在中间
一个字母只表示一个角
在靠近顶点的处画上弧线, 并写上数字 在靠近顶点的处画上弧线, 并写上希腊字母
2、下列说法正确的是( D) A.平角是一条直线 B.一条射线是一个周角 C.两条射线组成的图形叫做角 D.两边成一直线的角是平角
3.判断题
(1)直线是一个平角
()
×
(2)如图(1),点P不在∠AOB的内部 ( ) ×
A O
A
P
D
· · B
· B
EC
√
(3)如图(2), ∠ABC与∠DBE是同一个角( )
1.角的定义一: 有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这 两条射线叫做角的边。
2.角的定义二: 角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成 的图形。射线旋转时经过的平面部分叫角 的内部。
3.角的四种表示方法
表示方法 1、用三个大写的字母表示
2、用一个顶点的字母来表示
1
C
注后才能使用,并且只能表示 O
B
单独的一个角
上海沪科版初中数学七年级上册4.4 角ppt课件
角的定义(1)
角是由具有公共端点的两条射线组成的图形.
角的顶点 角的外部
角的边
射边线
角的内部
顶点
射边线
那么如何表示一个角呢?
A
这个角
该叫什
O
么名字
B
呢?
角的表示方法
如
A
OB
∠∠AO B
A2
F
A1 M
∠∠A1M A2
AC
∠FAAC
∠BOA ∠A2MA1 ∠CAF
定
2、角也可以看做一条射 线绕端点旋转所组成的图
义 形。动
角的四种表示方法;
表示方法
用三个大写的字母 表示
B
图标
A
C
记法
ABC
用一个顶点的字母
表示
o
o
用希腊字母表示
α
α
用一个数字表示
1
1
注意事项
顶点字母在中间
顶点处只有 一个角时
在靠近顶点处 画弧线, 注上数字
或希腊字母
直角、平角、周角 射线 OA绕点O 旋转90度后, B
叫做角,这个公共端点叫做角的顶点,这 两条射线叫做角的边。
2.角的定义二: 角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成 的图形。射线旋转时经过的平面部分叫角 的内部。
3.角的四种表示方法
表示方法
1、用三个大写的字母表示
注意事项 表示顶点的字母要写在中间
2、用一个顶点的字母来表示
∠O
∠M
∠A
角的符号+三个大写字母
角的符号+ 表示顶点的字母
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.4 角
当心“角”下有陷阱
初学角的相关概念及简单运算,不少同学容易犯这样那样的错误,现分类点击如下.
一、与角的表示有关的错误
例1 如图1,以A 点为顶点的角有几个?把它们表示出来.
图1
错解:以A 点的角有3个,分别是BAD 、CAD 、A.
剖析:错解的主要原因是没有切实掌握对角任何表示.实际上,当一个顶点含有多个角时,不能用顶点的一个大写字母来表示角,而要用三个字母.
正解:以A 为顶点的角有三个:分别是∠BAD 、∠DAC 、∠BAC.
二、角单位换算中的错误
例2(1)把26.2°转化为度分、秒表示的形式;(2)把33°24′转化成度表示的形式. 错解:(1)26.29°=26°2′;(2)33°24′=33.24°.
剖析:错解是习惯性地把度、分、秒之间的进制当成10进制。
角度是60进制,在进行转化时,整数部分保留,小数部分向下一级单位转化,而且要牢记1°=60′,1′=60″, 1°=3600″或
1″=(36001)°,1″=(601)′,1′=(60
1)°这些基本常识. 正解:(1)26.2°=26°+0.2°=26°+0.2×60′=26°+12′=26°12′. (2)33°24′36″=33°+24′=33°+24×(
601)°=33°+0.4°=33.4°. 三、角的计算方面的错误
例3计算: (1)33°52′+21°50′;
(2)108°8′-36°56′;
(3) 20°23′×2 (4)15°3′÷7.
错解: (1) 33°52′+21°50′=55°2′; (2) 108°8′-36°56′=.71°52′;
(3)20°23′×2=20.46°.
剖析:度、分、秒有关角计算,应把度、分、秒单独计算.还要注意度、分、秒之间是60进制的.(1)、(2)错解在把度、分之间的换算当成100进制了.而(3)把分直接按十进制的计算了.
正解:(1) 33°52′+21°50′=(33°+21°)+(52′+50′)=54°+102′=55°42′.
(2) 108°8′-36°56′=(107°+68′)-(36°+56′)=(107°-36°)+(68′-56′)=71°12′.
(3)20°23′×2=20°×2+23′×2=40°+46′=40°46′.
四、忽视对多种情况的讨论
例4 已知∠AOB=20°,∠BOC=30°.求∠AOC的度数.
错解:∠AOC=∠AOB+∠BOC=20°+30°=50°.
剖析:错解忽视了可能存在的两种情况,造成了漏解.考虑问题时,要细致全面。
正解:有两种情况.
根据图2可得∠AOC=∠AOB+∠BOC=50°;
根据图3可得∠AOC=∠B0C-∠AOB=10°.
图2 图 3
五、不理解方位角的概念
例 5下列说法中,正确的是().
(A)东偏北 30°(B)北偏东 30°(C)南偏北 120°(D)北偏南 60°
错解:选(A)、(C)、(D).
剖析:方位角是物体运动方向与正北(或正南)方向之间的夹角.更没有像南偏北与北偏南这样的说法,因此,(A)、(C)、(D)均不对,故应选(B).。
