高数考研大纲
考研高数二考试大纲

考研高数二考试大纲一、行列式行列式的概念和基本性质、行列式按行(列)展开定理。
考试要求1.了解行列式的概念,掌握行列式的性质。
2.会应用行列式的性质和行列式按行(列)展开定理计算行列式。
二、矩阵矩阵的概念、矩阵的线性运算、矩阵的乘法、方阵的幂、方阵乘积的行列式、矩阵的转置、逆矩阵的概念和性质、矩阵可逆的充分必.要条件、伴随矩阵、矩阵的初等变换、初等矩阵、矩阵的秩、矩阵的等价、分块矩阵及其运算。
考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质。
2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质。
3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵。
4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法。
5.了解分块矩阵及其运算。
三、向量向量的概念、向量的线性组合和线性表示、向量组的线性相关与线性无关、向量组的极大线性无关组、等价向量组、向量组的秩、向.量组的秩与矩阵的秩之间的关系、向量的内积、线性无关向量组的的正交规范化方法。
考试要求1.理解n维向量、向量的线性组合与线性表示的概念。
2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法。
3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩。
4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系。
5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法。
四、线性方程组考研数学二考试大纲是什么,我们再来看看线性方程组。
线性方程组的克拉默(Cramer)法则、齐次线性方程组有非零解的充分必要条件、非齐次线性方程组有解的充分必要条件、线性方程组解的性质和解的结构、齐次线性方程组的基础解系和通解、非齐次线性方程组的通解。
2015考研高数二+线代课本大纲

高数部分:(配同济六版教材)第一章函数与极限(考研必考章节,其中求极限是本章最重要的内容,要掌握求极限的集中方法)第一节映射与函数(一般章节)一、集合(不用看)二、映射(不用看)三、函数(了解)注:P1--5 集合部分只需简单了解P5--7不用看P7--17 重点看一下函数的四大性态:单调、奇偶、周期、有界P17--20 不用看P21 习题1.11、2、3大题均不用做4大题只需做(3)(5)(7)(8)5--9 均做10大题只需做(4)(5)(6)11大题只需做(3)(4)(5)12大题只需做(2)(4)(6)13做14不用做 15、16重点做17--20应用题均不用做第二节数列的极限(一般章节本章用极限定义证的题目考纲不作要求,可不看)一、数列极限的定义(了解)二、收敛极限的性质(了解)P26--28 例1、2、3均不用证p28--29 定理1、2、3的证明不用自己证但要会理解P30 定理4不用看P30--31 习题1-21大题只需做(4)(6)(8)2--6均不用做第二节数列的极限(一般章节本章用极限定义证的题目考纲不作要求,可不看)一、数列极限的定义(了解)二、收敛极限的性质(了解)P26--28 例1、2、3均不用证p28--29 定理1、2、3的证明不用自己证但要会理解P30 定理4不用看P30--31 习题1-21大题只需做(4)(6)(8)2--6均不用做第三节(一般章节)(标题不再写了对应同济六版教材标题一、(了解)二、(了解)P33--34 例1、2、3、4、5只需大概了解即可P35 例6 要会做例7 不用做P36--37 定理2、3证明不用看定理3’4”完全不用看p37习题1--31--4 均做5--12 均不用做第四节(重要)一、无穷小(重要)二、无穷大(了解)p40 例2不用做p41 定理2不用证p42习题1--41做2--5 不全做6 做7--8 不用做第五节(注意运算法则的前提条件是各自存在)p44推论1、2、3的证明不用看p48 定理6的证明不用看p49 习题1--51题只需做(3)(6)(7)(8)(10)(11)(13)(14)2、3要做4、5重点做6不做第六节极限存在准则(重要) 两个重要极限(重要两个重要极限要会证明p50 准则1的证明要理解p51 重要极限一定要会独立证明(经典重要极限)p53另一个重要极限的证明可以不用看p55--56柯西极限存在准则不用看p56习题1--71大题只做(1)(4)(6)2全做3不用做4全做,其中(2)(3)(5)重点做第七节(重要)p58--59 定理1、2的证明要理解p59 习题1--7 全做(就是全做)第八节(基本必考小题)p60--64 要重点看第八节基本必出考题p64 习题1--81、2、3、4、5要做其中4、5要重点做6--8不用做第九节(了解)p66--67 定理3、4的证明均不用看p69 习题1--91、2要做3大题只做(3)——(6)4大题只做(4)——(6)5、6均要重点做第十节(重要,不单独考大题,但考大题会用到)一、(重要)二、(重要)p72三、一致连续性(不用看)p74习题1--101、2、3、5要做,要会用5的结论。
2019版2019考研数二大纲 高数-5页word资料

考研的可以留着(数二大纲)考研数学二大纲编辑词条考研数学二大纲根据工学、经济学、管理学各学科、专业对硕士研究生入学所应具备数学知识和能力的不同要求,硕士研究生入学统考数学试卷分为3种,其中针对工学门类的为数学一、数学二,针对经济学和管理学门类的为数学三。
目录1 考试内容2 考试信息展开1 考试内容1.1 函数、极限、连续1.2 一元函数微分学1.3 一元函数积分学1.4 多元函数微积分学1.5 常微分方程1.6 考试内容之线性代数1.7 二次型2 考试信息2.1 考试科目2.2 考试形式和试卷结构1 考试内容编辑本段1.1 函数、极限、连续考试内容:函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限和右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1. 理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.2. 了解函数的有界性、单调性、周期性和奇偶性.3. 理解复合函数及分段函数的概念了解反函数及隐函数的概念4. 掌握基本初等函数的性质及其图形,了解初等函数的概念.5. 理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系.6. 掌握极限的性质及四则运算法则7. 掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8. 理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9. 理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10. 了解连续函数的性质和初等函数一的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.1.2 一元函数微分学考试要求1. 理解导数和微分的概念,理解导数和微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2. 掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3. 了解高阶导数的概念,会求简单函数的高阶导数.4. 会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5. 理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6. 掌握用洛必达法则求未定式极限的方法.7. 理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8. 会用导数判断函数图形的凹凸性(注:在区间(a,b)内,设函数f(x)具有二阶导数。
同济高数第七版上册考研数学考纲.doc
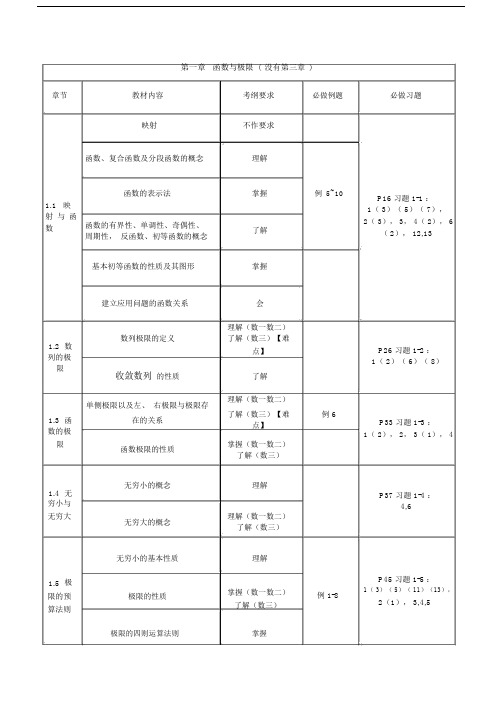
第一章函数与极限(没有第三章)章节教材内容考纲要求必做例题映射不作要求函数、复合函数及分段函数的概念理解函数的表示法掌握例5~10 1.1 映射与函函数的有界性、单调性、奇偶性、数了解周期性,反函数、初等函数的概念基本初等函数的性质及其图形掌握建立应用问题的函数关系会理解(数一数二)1.2 数数列极限的定义了解(数三)【难点】列的极限收敛数列的性质了解单侧极限以及左、右极限与极限存理解(数一数二)了解(数三)【难例 6 1.3 函在的关系点】数的极限函数极限的性质掌握(数一数二)了解(数三)1.4 无无穷小的概念理解穷小与无穷大无穷大的概念理解(数一数二)了解(数三)无穷小的基本性质理解1.5 极掌握(数一数二)限的预极限的性质例 1-8算法则了解(数三)必做习题P16 习题 1-1 :1( 3)( 5)( 7),2( 3), 3, 4( 2), 6(2), 12,13P26 习题 1-2 :1( 2)( 6)( 8)P33 习题 1-3 :1( 2), 2, 3( 1), 4P37 习题 1-4 :4,6P45 习题 1-5 :1( 3)( 5)( 11)(13),2(1), 3,4,5极限的四则运算法则掌握章节1.6 极限存在准则,两个重要极限1.7 无穷小的比较1.8 函数的连教材内容考纲要求必做例题必做习题极限存在的两个准则(夹逼准则、掌握(数一数二)单调有界数列必有极限)了解(数三)P52 习题 1-6 :利用两个重要极限求极限的方法掌握【重点】例1~41( 4)( 6), 2,4 柯西审敛原理不作要求无穷小阶的定义及无穷小量的比较方法例 1~5P55 习题 1-7 :掌握【重点】(熟记例1,3,4 (1), 51,2 的结论)一些重要的等价无穷小及其性质函数连续性的概念理解【重点】(含左连续与右连续)P61 习题 1-8 :续性与间断点1.9 连续函数的运算与初等函数的连续性1.10 闭区间上连续函数的性质总复习一函数间断点的分类与判别(第一类间断点与第二类间断点)函数间断点的和、差、积、商的连续性反函数与复合函数的连续性初等函数的连续性有界性与最大值最小值定理,零点定理与介值定理一致连续性总结归纳本章的基本概念、基本定理、基本公式、基本方法3(1), 4,5会【重点】例 1~5例 1P65 习题 1-9 :3( 3)( 5)( 7)( 8)了解(会利用连续4( 4)( 5)( 6)( 7)性求极限)例 2~4( 8)56例 5~8理解【重点】(会灵活应用这些性例 1质)P70 习题 1-10 :1,2,3,4,5不作要求P70 总习题一:3,5,9 ( 2)( 4)( 6)( 7)( 8), 10, 11,12,13,14章节2.1 导数概念2.2 函数的求导法则2.3 高阶导数2.4 隐函数及由参数方程所确定的函数的导数,相关变化率第二章导数与微分教材内容考纲要求导数的定义理解【重点】了解(仅数学一数导数的物理意义学二要求)(会用导数描述物理量)理解(数一数二)导数的几何意义了解(数三)(会求平面曲线的切线方程和法线方程)导数的经济意义了解(仅数三要求)单侧导数以及单侧可导理解与可导的关系函数的可导性与连续性的关系理解【重点】函数的和、差、积、商掌握的求导法则反函数的求导法则掌握复合函数的求导法则掌握【重点】(基本求导法则与导数公基本求导法则与导数公式式要非常熟悉)分段函数的求导会【重点】高阶导数的概念了解【重点】简单函数的高阶导数会(归纳法,莱布尼茨公式)隐函数的导数(对数求导法则)会【重点】由参数方程所确定的会【重点】(仅数函数的导数一数二要求)相关变换率不作要求必做例题例 1~6引例 1例8,9,引例 2例 7例 10,11例 1~15例 1~8(记住例 4,5 的结论)数一、二做例1~9数三做例 1~5必做习题P83 习题 2-1 :6,7,13,16(2),17,18,19P94 习题 2-2 :2( 9), 3( 3),6( 9)( 10),7(8),8( 4), 9,10 ( 2),11(4)( 9)P100 习题 2-3 :1( 3),3(2),4( 2)8,9,10 ( 2), 12P108 习题 2-4 :1( 3), 2, 3(4)4( 1)( 3), 5( 2),8( 3)数三不用做5,8章节2.5 函数的微分总习题二4.1 不定积分的概念与性质4.2 换元积分法4.3 分部积分法4.4 有理函数的积分教材内容考纲要求必做例题必做习题微分的定义、几何意义掌握(数一数二)了解(数三)基本初等函数的微分方程掌握例 1~6P120 习题 2-5 :1,3 ( 3)( 6),微分运算的法则了解(会求4( 4)( 6)( 7)(微分形式不变性)函数的微分)微分在近似计算中的应用不作要求P122 中习题二:总结归纳本章的基本概念、基2, 3,6( 1), 7,11 本定理、基本公式、基本方法12(1), 13,14数三不做 12,13第四章不定积分原函数与不定积分的概念理解P192 习题 4-1 :掌握【重点】(熟例 1~31( 1), 2( 5)( 8)基本积分表( 13)记)5~15( 17)( 19)( 21)( 25),5,7 不定积分的性质掌握第一类换元法(凑微分法)例 1~20P207 习题 4-2 :掌握【重点】(熟2( 4)( 6)( 11)( 15)记 P205 公式,双曲( 16)( 17)( 19)( 21)第二类换元法代换不作要求)例 21~24( 30)( 32)(34)( 36)( 37)分部积分法适用场合及形式掌握【重点】例 1~9习题 4-3: 2,5,6,9 ,12,17,18,21,22,24有理函数的积分会(仅数一数二要例 1~5,习题 4-4 :可化为有理函数的积分求)5~8 4,6,8,12,20,23(三角函数有理式和简单无理函数)章节教材内容考纲要求必做例题必做习题4.5 积分不作要求表的使用总习题四: 1,2,3总习题四总结归纳本章的基本概念、基本4( 1)( 5)( 9)( 10)定理、基本公式、基本方法( 12)( 14)( 16)( 19)( 21)( 25)(33)( 35)第五章定积分5.1 定积分的概念与性质定积分的定义与性质函数可积的两个充分条件定积分的近似计算掌握(数一数二)了解(数三)(性例 1质 6 会证明)习题 5-1 :理解【难点】4( 4), 5,7 ( 4), 11不作要求5.2 微积分基本公式5.3 定积分的换元法和分部积分法5.4 反常积分5.5 反常积分的审敛法积分上限函数及其导数牛顿 - 莱布尼茨共识定积分的换元法与分部积分法无穷限的反常积分无界函数的反常积分理解【重点】(定理会证明、会求导)掌握【重点】(定理会证明)掌握【重点】了解概念,会计算反常积分不作要求习题 5-2:3,5 (2), 6,7,8 ( 3)例 1~4,例 6 ( 8)( 11)( 12),11 ( 2 ),(记住结论),例 7,8 12,13,14,15,16例 1~4 习题 5-3 :例 5~7(记住结1( 4)( 7)( 10)( 18)论),例 8~11,( 19)( 21)( 25)( 26)例 12(记住结2,5,6,7 ( 10)( 11)论)( 13)习题 5-4 :例 1~71( 4)( 8)( 10) 2,3 (记住结论), 4总习题五 :1(1)(2)(4)(5),2, 总结归纳本章的基本概念、基总习题五本定理、基本公式、基本方法4(2)5(2),6(1),11(7)(9)(10),12, 13,1415,18第六章定积分的应用章节教材内容考纲要求必做例题必做习题6.1 定积分元素法理解的元素法平面图形的面积(直角坐标情例 1~5 习题 6-2 :形、极坐标情形)会1(1)(4), 2(1), 4,体积:数学三只要6.2 定积分5(1)体积(旋转体的体积、平行截求旋转体的体积在几何学上例 6~10 7, 9, 11, 12, 面面积为已知的立体的体积)的应用15(1)(3)16, 19, 21, 22, 28 平面曲线的弧长会(数一数二)例 11~15 数三不做 22,286.3 定积分用定积分求变力做功、习题 6-3 :在物理学上会(数一数二)例 1~5水压力、引力5, 11 的应用总习题六总结归纳本章的基本概念、基总习题六 : 本定理、基本公式、基本方法1,2,4,5,6,7,9第七章微分方程7.1 微分方程的基本概念7.2 可分离变量的微分方程7.3 齐次方程7.4 一阶线性微分方程7.5 可降阶的高阶微分方程微分方程的阶、解、通解、初始条件和特解可分离变量的微分方程的概念及其解法一阶齐次微分方程的形式及其解法可化为一阶齐次微分方程的形式及其解法一阶线性微分方程的形式及其解法伯努利方程的形式及其解法用降阶法解下列形式的微分方程:y (n) f ( x), y n f (x, y' )习题 7-1 : 1(3)(4)了解例 1,2 2(2)(4), 3(2),4(3),5(1), 7习题7-2 :掌握例 1~4 1(3)(4)(5)(7)(9), 2(3)(4)掌握【重点】例 1,2习题 7-3:1(1)(5), 2(2)不作要求习题 7-4:掌握(熟记公式)例 1,3 1(3)(5)(8)(10),2(1)(3), 3 ,7(3)会(仅数一)例 4 8(5)例习题 7-5:会(仅数一数二)1,3,5,1(3)(4)(7), 2(2)6y '' f ( y, y' )必做例章节教材内容考纲要求题7.6 高阶线性线性微分方程的解的结构:齐理解(数一数二)次线性微分方程与非齐次线性了解(数三)微分方程微分方程的解的性质【难点】二阶常系数齐次线性微分方程会解【重点】(特征例 1~3 方程、求通解的步骤)7.7 常系数齐次线性微分方程会(数一数二)例 6~7 n 阶常系数齐次线性微分方程7.8 常系数非二阶常系数齐次线性微分方程中自由项为:多项式、指数函会解【重点】(数三齐次线性微分例 1~4 数、正弦函数、余弦函数以及不要求和与积)方程它们的和与积*7.9 欧拉方程欧拉方程的形式和通解会(数一数二)*7.10 常系数线性微分方程不作要求组解法举例总结归纳本章的基本概念、基总习题七本定理、基本公式、基本方法必做习题习题 7-6 :1(3)(6), 3, 4(2), 5习题 7-7:1(1)(4)(9),2(2)(4)数三不做1(9)习题 7-8:1(2)(4)(7)(9)2(2)(4)6习题 7-9:5, 8总习题七:1(1)(2)(4), 23(2), 4(1)(2)(7)5(3)(4), 6, 8。
考研高数上册所有内容

2013考研数学导学讲义(高数上)——之极限、微分学部分南京海天 王君甫第一章 函数 极限 连续第一节 函 数一、 集合 二、 区间与邻域区间:设,a b 都是实数,且a b <.数集{}x a x b <<称为开区间,记作(,)a b ,即(,)a b ={}.x a x b <<其中,a b 称为开区间(,)a b 的端点,这里(,),(,)a a b b a b ∉∉数集{}x a x b ≤≤称为闭区间,记作[,]a b ,即[,]a b ={}.x a x b ≤≤其中,a b 称为闭区间[,]a b 的端点,这里[,],[,]a a b b a b ∈∈类似地:有限区间 [,)a b ={}.x a x b ≤< (,]a b ={}.x a x b <≤ 无限区间 [,){},a x x a +∞=≥ (,)b -∞={}.x x b <(,)R =-∞+∞ 邻域:以点a 为中心的任何开区间称为点a 的邻域,记作()U a .设δ是任一正数,则开区间(-,)a a δδ+就是点a 的一个邻域,称为点a 的δ邻域,记作(,),U a δ即(,){}{}. U a x a x a x x a a δδδδ=-<<+=-<称为邻域的中心,δ称为邻域的半径.点a 的去心δ邻域,记作(,),(,)={0<<}.U a U a x a δδδ-oo即 点a 的左δ邻域(,)a a δ-,点a 的右δ邻域(,)a a δ+.三、 函数的概念定义:设,x y 是两个变量,D 是一个给定的数集,如果,x D y ∀∈按照一定的法则总有唯一确定的数值与之对应,则称y 是x 的函数,记作()y f x =,数集 D 称为函数的定义域,x 叫做自变量,y 叫做因变量.y 的取值范围叫函数的值域.1. 反函数:设函数 ()y f x =的定义域为f D ,值域为f V . 反过来,如果把 y 看作自变量,x 看作因变量,即,f y V ∀∈ 存在唯一的f x D ∈与之对应,对应法则记为1f -,得到新函数1()x f y -=,称 1()x f y -=为函数()y f x =的反函数.注意:(1) 只有一一对应的函数才有反函数()⇒单调函数一定有反函数 (2) 原函数与反函数的图像关于直线 y x =对称 2. 基本初等函数(6类函数的图像及性质) (1) 常值函数 y c =,(x R ∈)(2) 幂函数 ()a y x a R =∈ (掌握1,1,2,3a =-的函数图像及性质) (3) 指数函数 (0,1),(0,)x y a a a x R y =>≠∈∈+∞且(4) 对数函数 log (0,1)(0,),a y x a a x y R =>≠∈+∞∈且 与指数函数互为反函数. 记 x e exp ,log ln e x x x ==(5) 三角函数 sin ,cos ,tan ,cot ,()11sec ,csc cos sin y x y x y x y x y x y x x x========图像及性质 (6) 反三角函数arcsin ,arccos ,arctan ,cot ()y x y x y x y arc x ====图像及性质 3. 复合函数:若(),(),()y f u u x x ϕϕ==当 的值域落在()f u 的定义域内时,称 [()]y f x ϕ=是由中间变量 u 复合成的复合函数.4. 初等函数:由基本初等函数经过有限次的四则运算和有限次的复合步骤所构成的并能用一个式子表达的函数. 5.非初等函数:a) 常见的分段函数b) 符号函数sgn x c) 狄利克雷函数()D x d) 黎曼函数()R x 四、 函数的基本性质1.有界性:若0,,(),().M x I f x M f x I ∃>∀∈≤则称 在 上有界反之,若不存在这样的正数,().M f x I 则称 在 上无界 2. 单调性:1212()()x x f x f x <⇒< 单调增 1212()()x x f x f x <⇒≤ 单调不减 通常根据导数来判定函数单调性 3. 奇偶性:()()f x f x -= 偶函数 ()()f x f x -=- 奇函数注意:定义域一定要对称;通常按定义判断函数奇偶性 运算性质:奇函数±奇函数=奇函数;偶函数±偶函数=偶函数;奇函数()⨯÷奇函数=偶函数;偶函数()⨯÷偶函数=偶函数;奇函数()⨯÷偶函数=奇函数;4. 周期性:∃非零常数T ,()()f x T f x += 通常按定义判断函数周期性例 判别下列函数的奇偶性(1) ln(y x = (2) 11()(),0,1,()12xy F x a a F x a =+>≠-其中 为奇函数第二节 极 限一、数列极限定义:lim 0,0,,n n n x a N n N x a εε→∞=⇔∀>∃>>-<使时恒有 极限存在与前有限项的取值无关,即lim lim ()n k n n n x x k +→∞→∞=其中为自然数 数列极限的性质:1. 唯一性 lim ,lim n n n n x A x B A B →∞→∞===若,则.(想想为什么?)2. 有界性 lim ,0,||n n n x A M x M →∞=∃><若则使得.(想想为什么?) 收敛数列一定有界,但是有界数列不一定收敛. 如{1,1,1,1,,1,1}.---L3. 保号性如果 lim 0(0),00(0)n n n n x a a N n N x x →∞=><⇒∃>>><或,当时,都有或 .(想想为什么?)4. 收敛数列与子数列的关系lim lim k n n n k x A x A →∞→∞=⇒=若 反之,不一定.5. 数列极限存在准则(I) 夹逼准则 如果数列{},{}{}n n n x y z 及满足下列条件: a) 从某项起,即00,n N n n ∃∈>当 时,有,n n n y x z ≤≤b) lim ,lim ,n n n n y a z a →∞→∞==那么数列{}n x 的极限存在,且lim n n x a →∞=.(II) 单调有界收敛准则 单调有界数列必有极限 例1 证明 222111lim ()12n n n n n n πππ→∞+++=+++L L例2 证明 L 的极限存在,并求该极限.二、 函数极限 1. 函数当0x x →时的极限定义1:设函数()f x 在点0x 的某一去心邻域内有定义.如果存在常数A ,对于任意给定的正数ε(不论有多小),总存在正数δ,使得当x 满足不等式00x x δ<-<时,对应的函数值()f x 都满足不等式()f x A ε-<,那么常数A 就叫做函数()f x 当0x x →时的极限,记作0lim ()()()x x f x A f x A x x →=→→或 当简述:00lim ()0,0,0()xxf x A x x f x A εδδε→=⇔∀>∃><-<-<当 时,有 注意:a) 上述极限表示x 既从0x 的左侧又从0x 的右侧趋向于0x 的,b) 当x 从0x 的左侧(即00x x x δ-<<)趋向于0x 时,那么A 就叫做函数()f x 当0x x →时的左极限,记作00lim ()()x x f x A f x A --→==或 ;类似地,定义右极限,00lim ()()x x f x A f x A ++→==或c) 极限存在与()f x 在点0x 有无定义或定义的值无关. d) 0lim ()x xf x A →=⇔00lim ()lim ()x x x x f x f x A +-→→== 2. 函数当x →∞时的极限定义2:设函数()f x 当x 大于某一正数时有定义.如果存在常数A ,对于任意给定的正数ε(不论有多小),总存在正数X ,使得当x 满足不等式x X >时,对应的函数值()f x 都满足不等式()f x A ε-<,那么常数A 就叫做函数()f x 当x →∞时的极限,记作lim ()()()x f x A f x A x →∞=→→∞或 当简述:lim()0,0,()x f x A X x X f x A εε→∞=⇔∀>∃>>-<当 时,有 注意:a) x →∞既表示x →+∞也表示x →-∞ b) lim ()x f x A →∞=⇔lim ()lim ()x x f x f x A →+∞→-∞== 3. 函数极限的性质(1) 唯一性:若lim (),lim ()f x A f x B ==,则A B =(2) 局部有界性:若0lim ()x xf x A →=,则0,0M δ∃>>,使00||x x δ<-<时,|()|f x M ≤(3) 局部保号性:若0lim (),0xxf x A A →=>,则0000(),()()0U x x U x f x ∃∈>, (4) 函数极限与数列极限的关系(归结原则):若000lim (),lim ()n n x x n f x A x x x x →→∞==≠且,则0lim ()lim ()n n x xf x f x A →∞→== (5) 四则运算:若 lim (),lim ()f x Ag x B ==,则 lim[()()];lim[()()]kf x lg x kA lB kf x g x kA B ±=±⋅=⋅;()lim (0)()f x AB g x B=≠. 两个常用结论:a) ()lim lim ()0lim ()0;()f xg x f x g x =⇒=存在, b) ()limlim ()0lim ()0;()f x f xg x g x ≠=⇒==A 0, 事实上, 除了上述法则外,还应注意:==();()=±±⨯÷⨯÷存在不存在不存在;不存在不存在不一定;存在不存在=不一定不存在不存在不一定;4. 无穷小量和无穷大量 (1) 无穷小量1) 定义:若lim ()0,x f x →*=称()f x 为x 趋于*的无穷小量. 特别地,0也可以看作无穷小量.2) 无穷小量的比较:设lim ()0,lim ()0.x x αβ== 高阶:若()lim0,()x x βα=则称()x β为()x α的高阶无穷小量记为()(()).x o x βα= 同阶:若()lim 0,()x C x βα=≠则称()x β与()x α是同阶无穷小量. 等价:若()lim1,()x x βα=则称()x β与()x α是等价无穷小量.记为()x x αβ~(). 无穷小的阶:若()lim0,[()]kx C x βα=≠则称()x β是()x α的k 阶无穷小量.例 已知当0x →时,2x n e ax --与 是等价无穷小,求n3) 无穷小量的性质:a) 有限个无穷小量之和仍为无穷小量; b) 常数与无穷小量之积仍为无穷小量; c) 有限个无穷小量之积仍为无穷小量; d) 无穷小量与有界变量之积仍为无穷小量; (2) 无穷大量1) 定义:若lim (),x f x →*=∞称()f x 为x 趋于*的无穷大量2) 无穷大量与无界变量的关系:无穷大量⇒无界变量,反之不一定成立,数列{}n x 是无穷大量:0,,n M N n N x M ∀>∃>>当 时,都有 数列{}n x 是无界变量:0,,.N M N x M ∀>∃>使反例:数列[1(1)]n n x n =+-是无界变量,但不是无穷大量. 3) 无穷大量与无穷小量的关系:无穷大量的倒数是无穷小量;无穷小量(除0外)的倒数是无穷大量. 注意:a) 无穷大量之和(同方向)、之积为无穷大量;无穷大量之差(同方向)、之商结果不一定;无穷大量与有界变量之积不一定(如1lim 1x x x→∞⋅=),但若lim ()0,lim (),lim ()()f x a g x f x g x =≠=∞=∞则;无穷大量与有界变量之和、之差为无穷大量. b) 在求极限的过程中,x →∞当时,无穷大量 ln (,0,1)x x x x a x a αβαβ>>===三者趋于无穷大的快慢程度不一样决定了三者之间比值的极限也不一样.对于数列无穷大量之间有 ln !(0,1)n n n n a n n a αα>>====如 lim;lim ;lim ;ln ln x xx x x x a a x x x βααβ→∞→∞→∞=∞=∞=∞ ln ln lim0;lim 0;lim 0;x x x x x x x x x a aααββ→∞→∞→∞=== 例lim 1)ln n n n→∞= 5. 求极限的步骤与方法步骤:对于函数极限:步1)能否有理化;步2)考虑等价无穷小代换;步3)考虑重要极限;步4)考虑洛必达法则;步5)利用泰勒公式转化.对于数列极限:步1)能否连续化求对应函数极限;步2)夹逼准则;步3)单调有界准则;步4)利用定积分的定义. 方法1:利用有理运算法则求极限 常用的方法 a) 分子、分母有理化后约分 b) 多项式比值的极限101101,()lim ,().m m m m n n x nn a n m b P x a x a x a n m Q x b x b x b n m --→∞⎧=⎪⎪+++⎪==>⎨+++⎪∞<⎪⎪⎩L L 当,0,当,当 例x = 方法2:利用重要极限 a) 0sin sin(())lim1lim 1(lim ()0)()x x x x x x ϕϕϕ→=⇒==推广形式当时 b) 11()()lim(1)lim(1())(lim ()0);lim(1())(lim ()()).x xx x A x e x e x x e x x A ϕψϕϕϕϕψ→+=⇒+==+=⋅=推广形式当时当时c) 1x = 例 11cos0arcsin lim()x x x x-→= 方法3:利用等价无穷小代换求极限 常见的等价无穷小,当0x →时,2sin tan arcsin arctan ln(1)111ln ;(1)1;1cos .2x xx x x x x x e a x a x x x x αα+--++-:::::::::注意:有相应的推广形式求极限,等价无穷小只能在乘除法中替换,不能用于加减法.例1 123(1)1limcos 1x x x →+--=例2 0tan 3lim 2x xx→= 方法4:利用洛必达法则(0;0∞∞)设函数(),()f x g x 满足条件:(1)0lim ()0,lim ()0.(lim (),lim ())x x x x x x x xf xg x f x g x →→→→===∞=∞或 (2)00(),()()0;f x g x x x g x '≠都在 的邻域内可导(在 点除外)且 (3)0()lim()x xf xg x →'∞'存在(或 ) 则00()()limlim ()()x xx x f x f x g x g x →→'=' 推广形式求000;;1;;0;∞⋅∞∞-∞∞型极限,前二者可直接化为0;0∞∞型极限,后三者可用幂指数函数极限的方法即()()ln ()lim(())lim g x g x f x f x e =再进一步化为0;0∞∞型极限求. 注意:一般来说对于振荡函数求极限不用洛必达法则.如 当x →∞时,极限式中含有sin ,cos x x ; 当0x →时,极限式中含有11sin ,cos x x. 例方法5:利用泰勒公式展开求极限2332332433433233221();sin ();arcsin ();266cos 1();tan ();arctan ();24!33(1)ln(1)();(1)1().232xx x x e x o x x x o x x x o x x x x x x o x x x o x x x o x x x x x o x x x x o x αααα=+++=-+=++=-++=++=-+-+=-+++=+++例1 2220cos lim[ln(1)]x x x ex x x -→-=+- 例2x →=方法6:利用夹逼准则求极限例_________(0)i n a =>方法7:利用单调有界准则求极限 例 11sin (0,1,2,)n n x x x n π+=<<=L 证明lim n n x →∞存在,并求该极限方法8:利用定积分的定义求极限 例 111lim()12n n n n n→∞++++++L第三节 函数的连续性一、函数连续的概念1. 定义:设函数()y f x =在点0x 的某一邻域内有定义,如果000lim lim[(+)()]0,x x y f x x f x ∆→∆→∆=∆-=那么就称函数()y f x =在点0x 连续.常用定义:设函数()y f x =在点0x 的某一邻域内有定义,如果0lim ()(),x x f x f x →= 那么就称函数()f x 在点0x 连续.简述:()f x 在点0x 连续000,0,()()x x f x f x εδδε⇔∀>∃>-<-<当 时,有 左连续:000lim ()()()x x f x f x f x --→==右连续:000lim ()()()x x f x f x f x ++→==函数()f x 在点0x 连续()f x ⇔在点0x 左连续且右连续. 二、函数的间断点及类型1. 第一类间断点:左、右极限都存在的间断点可去间断点:左极限=右极限(000lim ()lim ()()x x x x f x f x f x +-→→=≠)跳跃间断点:左极限≠右极限(00lim ()lim ()x x x x f x f x +-→→≠)2. 第二类间断点:左、右极限中至少有一个不存在,只掌握两类 无穷间断点:0x x →时,()f x →∞.振荡间断点:0x x →时,()f x 振荡,例 01limsin x x→ 例 求函数2()lim n n n nn x x f x x x +--→∞-=+的间断点并指出其类型.三、连续函数的性质1. 连续函数的和、差、积、商(分母不为0)及复合仍连续;2. 初等函数在其定义域内处处连续;3. 闭区间上连续函数的性质(往往用于证明方程中ξ的存在性以及方程的根问题)a) 有界性:若()f x 在[,]a b 上连续,则()f x 在[,]a b 上有界.b) 最值性:若()f x 在[,]a b 上连续,则()f x 在[,]a b 上必有最大值和最小值.c) 介值性:若()f x 在[,]a b 上连续,且()()f a f b ≠,则对()f a 及()f b 之间任意常数C ,至少存在一点(,)a b ξ∈,使得()f C ξ=.推论:若()f x 在[,]a b 上连续,则()f x 在[,]a b 上可取到介于最小值和最大值之间的任何值.d) 零点定理:若()f x 在[,]a b 上连续,且()()0f a f b ⋅<,则至少存在一点(,)a b ξ∈,使得()0f ξ=.例 设函数()f x 在(,)-∞+∞上连续,且()lim0x f x x→∞=,试证存在(,)ξ∈-∞+∞,使得()0.f ξξ+=证明:第二章 导数和微分第一节 导数和微分概念1. 导数的定义设函数()y f x =在点0(,)U x δ内有定义,当自变量x 趋近于0x 即x ∆趋于0时,相应地增量00()()y f x x f x ∆=+∆-与x ∆的比值的极限存在,称函数()y f x =在点0x 处可导,该极限称为()y f x =在点0x 处的导数,记作0()x x y f x =''或 .简述:000000()()()limlimx x x x f x x f x yf x y x x=∆→∆→+∆-∆''==∆∆ = 推广形式:0000000()()()()()lim lim x x h f x f x f x h f x f x x x h→→-+-'==- . 左导数:0000000()()()()()limlim x x h f x f x f x h f x f x x x h ---→→-+-'==- ; 右导数:0000000()()()()()limlim x x h f x f x f x h f x f x x x h+++→→-+-'==- . 可导⇔左、右导数都存在且相等. 例 研究函数()0f x x x ==在 处的导数.2. 微分的定义设有函数()y f x =,若函数的增量00()()y f x x f x ∆=+∆-可表示为()y A x o x ∆=∆+∆的形式,其中A 是不依赖于x ∆的常数,那么称函数()y f x =在点0x 处是可微的.A x ∆叫做函数()y f x =在点0x 相对于自变量的增量x ∆的微分,记作dy ,即.dy A x =∆函数可微的充要条件:()f x 在点0x 可微()f x ⇔在点0x 可导. 且0().dy f x dx '=简要证明:000()():()lim (),();x y o x y y A x o x A f x A dy f x dx x xx ∆→∆∆∆''⇒∆=∆+∆⇒=+⇒===∆∆∆即 00000():lim ()()()()().x y yf x f x y f x x x f x x o x x x αα∆→∆∆''''⇐=⇒=+⇒∆=∆+∆=∆+∆∆∆ 于是函数()y f x =的微分又可记作().dy f x dx '=3. 导数和微分的几何意义(会求曲线的切线方程和法线方程)1). 导数0()f x '在几何上表示曲线()y f x =在点00()x f x (,)处切线的斜率.2). 微分0()dy f x dx '=在几何上表示曲线()y f x =的切线的增量. 4. 连续、可导、可微之间的关系例 讨论函数1sin ,00,0x x xx ⎧≠⎪⎨⎪=⎩在点0x =处的连续性和可导性以及导函数的连续性.第二节 导数的计算1. 基本求导公式1)()0;C '= 2)1();x x ααα-'= 3)()ln ;x x a a a '= 4)();x x e e '= 5)1(log );ln a x x a '=6)1(ln );x x'= 7)(sin )cos ;x x '= 8)(cos )sin ;x x '=- 9) 2(tan )sec ;x x '= 10) 2(cot )csc ;x x '=- 11) (sec )sec tan ;x x x '=⋅12) (csc )csc cot ;x x x '=- 13)(arcsin )x '= 14)(arccos )x '=15)21(arctan );1x x '=+ 16)21(arccot ).1x x'=-+ 2. 求导法则1) 有理运算法则设(),()u u x v v x ==在x 处可导,则a) ()u v u v '''±=± b) ()u v u v uv '''⋅=+ c) 2()(0)u u v uv v vv''-'=≠ 例 22()5cos x x x'=+2) 复合函数求导法设()u x ϕ=在x 处可导,()y f u =在对应点处可导,则复合函数[()]y f x ϕ=在x 处可导,且()()dy dy du y f u x dx du dxϕ'''==⋅= 例 22sin 1x y x =+,求.dydx3) 隐函数求导法显函数:形如()y f x =,等号左端是因变量的符号,右端是含有自变量的式子,这种方式表达的函数称为显函数. 例如 sin ;ln x y x y x e ==+ 隐函数:由方程(,)0F x y =在一定条件下,当自变量x 取某区间内的任一值时,相应的总有满足这方程的唯一的y 值存在,那么就说方程(,)0F x y =在该区间内确定了一个隐函数.求导方法:设()y y x =是由方程(,)0F x y =所确定的隐函数的可导函数,为求得y ',可在方程(,)0F x y =两边对x 求导,可得到一个含有y '的方程,从中解出y '即可.例 设函数()y y x =由方程y e xy e +=所确定,求(0)y ''.4) 反函数求导法若函数()x f y =在区间y I 内单调、可导且()0f y '≠,则它的反函数1()y f x -=在区间{(),}x y I x x f y y I ==∈内也可导,且11[()]()f x f y -'='或1.dy dxdx dy= 证明:由于函数()x f y =在区间y I 内单调、可导(即连续)且()0f y '≠,则()x f y =的反函数1()y f x -=存在,且在对应区间{(),}x y I x x f y y I ==∈内也单调、可导(即连续).任取x x I ∈,给x 以增量(0,)x x x x x I ∆∆≠+∆∈,由1()y f x -=的单调性可知11()()0y f x x f x --∆=+∆-≠,于是有1y xx y∆=∆∆∆,因1()y f x -=连续,故0lim 0x y ∆→∆=,从而10011[()]limlim ()x y y f x x x f y y-∆→∆→∆'===∆'∆∆. 反函数二阶导公式:12131[]1()()[][()]()()[()][()]()[()]d f y f y d d f x f y f y dyf y f x dx dxdxf y f y dy--'''-'''''''=====-''. 5) 参数方程求导法设y 与x 的函数关系是由参数方程()()x t y t ϕψ=⎧⎨=⎩确定的,则称此函数关系所表达的函数为由参数方程所确定的函数.1().()dy dy dt dy t dx dx dt dx dt t dtψϕ'=⋅=⋅='参数方程二阶导公式:2223()()()()()()1()()()()()[][].()()()()()d y d dy d t d t dt t t t t t t t t dx dx dx dx t dt t dx t t t ψψψϕψϕψϕψϕϕϕϕϕϕ''''''''''''''--===⋅=⋅='''''例求参数方程arctan x y t⎧⎪=⎨=⎪⎩的二阶导数.6) 对数求导法若函数为()()g x y f x =形式,求dydx. 则对函数两边同时取对数得,ln ()ln ()y g x f x =()()()ln ()()[()ln ()()]()()y f x dy f x g x f x g x y y g x f x g x y f x dx f x ''''''⇒=+⇒==+ 例 设2sin (1)x y x =+,求y '.第三节 高阶导数定义:一般地,函数()y f x =的导数()y f x ''=仍然是x 的函数. 我们把()y f x ''=的导数叫做函数()y f x =的二阶导数,记作y ''或22d ydx,即22()()d y d dyy y dx dx dx''''==或类似地,二阶导数的导数叫做三阶导数,L L ,(1)n -阶导数的导数叫做n 阶导数,分别记作(4)(),,,n y y y'''L 或者3434,,,.n n d y d y d y dx dx dxL计算方法:I) 归纳法:即先求一阶导,二阶导,L ,最后归纳证明出n 阶导数. II) 莱布尼兹公式:()()()0()nn k n k k n k uv C u v -==∑III) 基本公式法:a) ()()[sin()]sin();[cos()]cos();22n n n n n n ax b a ax b ax b a ax b ππ+=+++=++ b) ()11!()(1);()n n n n x a x a +=-++ c) ()[(1)](1)(2)(1)(1).n n x n x αααααα-+=---++L IV) 利用泰勒级数:()()0000()0()()()()()!!()!n n nn n n n n f x f x f x x x a a n n n f x a n ∞==-==⋅∑其中表示展开式中次项的系数,则例 设2()56xf x x x =-+,求()()n f x .例 求函数2()ln(1)f x x x =+在0x =处的(2)n n >阶导数.第三章 微分中值定理与导数的应用第一节 微分中值定理一、罗尔定理1. 费马引理:设函数()f x 在点0x 的某一邻域0()U x 内有定义,并且在0x 处可导,如果对任意的0()x U x ∈,有00()()(()())f x f x f x f x ≤≥或,那么0()0f x '=.证明:不妨设0()x U x ∈时,0()()f x f x ≤(如果0()()f x f x ≥,可以类似地证明).于是,对于00()x x U x +∆∈,有00()()f x x f x +∆≤,从而当0x ∆>时,00()()0;f x x f x x +∆-≤∆当0x ∆<时,00()()0.f x x f x x+∆-≥∆根据函数()f x 在0x 可导的条件及极限的保号性,得00000()()()()lim 0,x f x x f x f x f x x++∆→+∆-''==≤∆00000()()()()lim 0.x f x x f x f x f x x --∆→+∆-''==≥∆所以0()0f x '=.证毕.2. 罗尔定理:如果函数()f x 满足: a) 在闭区间[,]a b 上连续; b) 在开区间(,)a b 内可导; c) 端点值相等,即()()f a f b =, 那么至少存在一点(,)a b ξ∈,使得()0f ξ'=.证明:由于()f x 在[,]a b 上连续,根据连续函数的最值定理知,()f x 有最大值M 和最小值m ,分两种情况讨论:1) M m =,此时()f x 在[,]a b 上必然取相同的值M ,即()f x M =. 由此得()0f x '=.因此,任取(,)a b ξ∈,有()0f ξ'=.2) M m >,因为()()f a f b =,所以M 和m 至少有一个不等于()f x 在区间[,]a b 端点处的函数值.不妨设()(())M f a m f a ≠≠若,可类似证明则必定至少存在一点(,)a b ξ∈使得()f M ξ=.因此任取[,]x a b ∈有()()f x f ξ≤,从而由费马引理有()0f ξ'=.证毕. 想想:几何意义?例 设函数()f x 在[,]a b 上连续,在(,)a b 内可导,且()f a b =,()f b a =,a 与b 同号. 求证:(,)a b ξ∃∈使()()f f ξξξ'=-.二、拉格朗日中值定理(条件比罗尔定理弱多了) 拉格朗日中值定理:如果函数()f x 满足: a) 在闭区间[,]a b 上连续; b) 在开区间(,)a b 内可导;那么至少存在一点(,)a b ξ∈,使得()()()()f b f a f b a ξ'-=-. 证明:构造辅助函数()()()()[()()]f b f a F x f x f a x a b a-=-+--,于是()F x 刚好符合罗尔定理的条件,则至少存在一点(,)a b ξ∈,使得()0F ξ'=,即()()()()f b f a F x f x b a-''=--,所以,()()()f b f a f b aξ-'=-,从而()()()()f b f a f b a ξ'-=-.证毕.想想:几何意义?拉格朗日定理是罗尔定理的推广形式(只需令()()f a f b =即可).例 证明当0x >时,ln(1).1xx x x <+<+ 并有离散形式:1ln(1)ln .1n n n n n<+-<+三、柯西中值定理柯西中值定理:如果函数()f x 及()F x 同时满足: a) 在闭区间[,]a b 上连续; b) 在开区间(,)a b 内可导; c) 对任一(,),()0,x a b F x '∈≠ 那么至少存在一点(,)a b ξ∈,使得()()()()()()f b f a f F b F a F ξξ'-='-.证明:首先注意到()()0.F b F a -≠因为()()()()F b F a F b a η'-=-,(,)a b η∈因假定()0,F η'≠又0b a -≠,所以()()0.F b F a -≠ 构造函数()()()()()[()()]()()f b f a x f x f a F x F a F b F a ϕ-=----,易验证()x ϕ适合罗尔定理的条件:()()0a b ϕϕ==;()x ϕ在闭区间[,]a b 上连续,在开区间(,)a b 内可导且()()()()().()()f b f a x f x F x F b F a ϕ-'''=-⋅-根据罗尔定理,可知至少存在一点(,)a b ξ∈,使得()0ϕξ'=,即()()()()0,()()f b f a f F F b F a ξξ-''-⋅=-由此得,()()()()()()f b f a f F b F a F ξξ'-='-.证毕.想想:几何意义?柯西中值定理是拉格朗日定理的推广形式(只需令()F x x =即可).例 设函数()f x 在[,]a b 上连续,在(,)a b 内可导,且 a 与b 同号,求证:,(,)a b ξη∃∈使()()2a bf f ξηη+''=.四、泰勒中值定理泰勒中值定理(拉格朗日型余项):如果函数()f x 在含有0x 的某个开区间(,)a b 内具有直到(1)n +阶的导数,则对任一(,)x a b ∈,有()20000000()()()()()()()()(),2!!n n n f x f x f x f x f x x x x x x x R x n '''=+-+-++-+L其中(1)10()()(),(1)!n n n f R x x x n ξξ++=-+是介于0x 与x 之间的某个值.(佩亚诺型余项): 如果函数()f x 在含有0x 的某个开区间(,)a b 内具有直到(1)n +阶的导数,则对任一(,)x a b ∈,有()20000000()()()()()()()()(),2!!n n n f x f x f x f x f x x x x x x x R x n '''=+-+-++-+L其中00()[()],()n n R x o x x x x =-→.如果取00x =,从而泰勒公式变成较简单的形式,称为麦克劳林公式. 常见的麦克劳林公式:(大纲要求掌握)201111()2!!!xn nn n e x x x o x x n n ∞==+++++=∑L3521212101111sin (1)()(1)3!5!(21)!(21)!n n n n n n x x x x x o x x n n ∞+++==-+-+-+=-++∑L2422201111cos 1(1)()(1)2!4!(2)!(2)!n n nn n n x x x x o x x n n ∞==-+-+-+=-∑L2311101111ln(1)(1)()(1),(1,1]2311n n n n n n x x x x x o x x x n n ∞+++=+=-+-+-+=-∈-++∑L2(1)(1)(1)(1)(1)(1)1(),2!!!nnn n n n x x x x o x x n n αααααααααα∞=---+--++=+++++=∑L L L (1,1)x ∈-例1 求极限1). 30sin cos lim sin x x x x x →-,2). 2220112lim .(cos )sin x x x x e x→+-例 2 设()f x 在[0,1]上三阶可导,且1(0)0,(1)1,()0.2f f f '===求证:(0,1),ξ∃∈使()24f ξ'''≥.第二节 导数的应用一、函数的单调性与曲线的凹凸性和拐点 1. 函数的单调性设函数()y f x =在闭区间[,]a b 上连续,在开区间(,)a b 内可导. a) 如果在(,)a b 内()0f x '>,那么函数()y f x =在[,]a b 上单调增加; b) 如果在(,)a b 内()0f x '<,那么函数()y f x =在[,]a b 上单调减少. 注意:在判断函数的单调性及求单调区间的过程中,第一步找出无定义的点、导数不存在的点以及导数为零的点;第二步根据这些点来划分定义区间,在每个区间上讨论()f x '的符号;第三步求出单调区间. 例1 证明:当1x >时,13.x>- 例2 试讨论方程ln 10x x e-+=的实根个数2. 函数的凹凸性及拐点1)定义:设函数()f x 在区间I 上连续,如果对I 上任意两点12,x x 恒有1212()()()22x x f x f x f ++<, 那么称()f x 在I 上的图形是凹的(几何形状?);如果恒有1212()()()22x x f x f x f ++>, 那么称()f x 在I 上的图形是凸的(几何形状?).判定方法:(联系几何意义记忆)设函数()f x 在[,]a b 上连续,在(,)a b 内具有一阶和二阶导数,那么: a) 若在(,)a b 内()0f x ''>,则()f x 在[,]a b 上是凹函数; b) 若在(,)a b 内()0f x ''<,则()f x 在[,]a b 上是凸函数.2)拐点定义:如果连续曲线()y f x =在点00(,())x f x 两侧的凹凸性相反,则称点00(,())x f x 为曲线()y f x =的拐点. 判定凹凸区间和拐点的方法: a) 求出函数()y f x =定义域; b) 求出二阶导数()f x '';c ) 求出二阶导数为零的点和使二阶导数不存在的点; d) 判断,确定出曲线凹凸区间和拐点.注意:拐点不一定是二阶导为零的点(反例y =0x =);二阶导为零的点也不一定是拐点(反例4y x =在点0x =). 例 求曲线43341y x x =-+的拐点及凹、凸区间.二、函数的极值与最值 1. 函数的极值.定义:设函数()f x 在点0x 的某邻域0()U x 内有定义,如果对于去心邻域()ox U 内的任一x ,有0()()f x f x <(或0()()f x f x >),那么就称0()f x 是函数()f x 的一个极大值(或极小值). 1) 极值的必要条件设函数()f x 在0x x =处取得极值,且0()f x '存在,则0()0f x '=. 导数为零的点称为驻点(或稳定点),注意:驻点不一定是极值点(例3y x =在点0x =),极值点也不一定是驻点(例函数y x =在点0x =). 2) 极值的充分条件 a) 第一充分条件设函数()f x 在0x 处连续,且在0x 的某去心邻域0(,)ox U δ内可导, I ) 若00(,)x x x δ∈-时,()0f x '>,而00(,)x x x δ∈+时,()0f x '<,则()f x 在0x 处取得极大值;II) 若00(,)x x x δ∈-时,()0f x '<,而00(,)x x x δ∈+时,()0f x '>,则()f x 在0x 处取得极小值;III ) 若0(,)ox x U δ∈时,()f x '的符号保持不变,则()f x 在0x 处没有极值. b) 第二充分条件若00()0,()0f x f x '''=≠,则()f x 在0x 处取得极值.其中当0()0f x ''>取极小值,当0()0f x ''<取极大值. c) 第三充分条件若(1)()0000()()()0,()0,n n f x f x f x f x -'''====≠L 则:I ) 当n 为偶数时()f x 在0x 处有极值;()0()0n f x >取极小值,()0()0n f x <取极大值.II) 当n 为奇数时()f x 在0x 处无极值. 2. 函数的最值函数在定义区间上的最大值和最小值称为函数的最值. 注意:函数的极值是局部概念;函数的最值是整体概念. 函数的极值不一定是最值;最值也不一定是极值. 判断函数极值和最值的方法: a) 求出函数的导数()f x ';b) 找出函数()f x 的全部驻点和无定义点或不可导点;c) 通过判断()f x '符号情况利用充分条件进行确定函数的极值情况; d) 确定出函数所有极值点和极值;并与所有不可导点的值以及区间的端点值作比较,确定出函数在整个区间上的最值. 例 求函数23()(1)1f x x =-+在[2,3]-上的极值与最值.三、函数图形的描绘和曲率 1. 函数的渐近线定义:当曲线()y f x =上的一个动点P 沿曲线移向无穷点或定点时,如果点P 到某定直线L 的距离趋向于零,那么该直线L 就称为曲线()y f x =的一条渐近线.1) 水平渐近线若lim ()(lim ())x x f x a f x a →+∞→-∞==或,则称y a =为曲线()y f x =的水平渐近线. 如:曲线arctan y x =有两条水平渐近线,.22y y ππ==-2) 垂直渐近线若00lim ()(lim ())x x x x f x f x +-→→=∞=∞或,则称0x x =为曲线()y f x =的垂直渐近线.如:曲线1(3)(2)y x x =+-有两条垂直渐近线3, 2.x x =-=3) 斜渐近线 若()lim x f x a x→∞=,lim[()]x f x ax b →∞-=,则称直线y ax b =+为曲线()y f x =的斜渐近线.(想想为什么?可联系几何意义) 例:求曲线32)y =的渐近线方程.2. 函数图形的描绘 方法步骤:a) 确定函数的定义域,并求出函数的一阶和二阶导数;b) 求出一阶和二阶导数为零的点,求出一阶和二阶导数不存在的点; c) 列表分析,确定曲线的单调性和凹凸性; d) 确定曲线的渐近线;e) 确定并描出曲线上的极值点、拐点、与坐标轴的交点、其它特殊点;f) 联接这些点画出函数的图形. 3. 曲率、曲率半径 (数三不要求) 曲率是描述曲线弯曲程度的量.曲率3223222;(())(1);((),())()y K y y x y y x y x K x x t y y t x y ''=='+''''''-===''+其中其中 ,曲率半径1R K=.2013考研数学导学讲义(高数上)——之积分学、方程部分南京海天 王君甫第四章 一元函数积分学第一节 基本概念、理论一、不定积分 1. 原函数定义1:如果在区间I 上,可导函数()F x 的导函数为()f x ,即对任一x I ∈,都有()()()()F x f x dF x f x dx '==或,那么()F x 就称为()f x 在区间I 上的原函数.原函数存在定理:如果函数()f x 在区间I 上连续,则()f x 在区间I 上一定有原函数.注意:a) 如果()f x 有一个原函数,则()f x 就有无穷多个原函数.即设()F x 是()f x 的原函数,则()+F x C 也是()f x 的原函数.b) 如果()F x 与()G x 都为()f x 在区间I 上的原函数,则()F x 与()G x 之差为常数,即()()F x G x C -=.2. 不定积分定义2:在区间I 上,()f x 的带有任意常数项的原函数,称为()f x 在区间I 上的不定积分,记为()f x dx ⎰.注意:a) 如果()F x 是()f x 的一个原函数,则()()f x dx F x C =+⎰,(C 为任意常数)b) 初等函数在定义域区间上连续,因而一定存在原函数,但它的原函数不一定是初等函数,也就是下列积分是积不出来的. 如:222sin cos ,,,sin(),cos(),.ln x x x dxe dx dx dx x dx x dx x x x-⎰⎰⎰⎰⎰⎰ 3. 基本性质a) 线性性质:[()()]()()af x bg x dx a f x dx b g x dx ±=±⎰⎰⎰; b) 微分与积分运算:4. 基本积分表1222221);2)(1);3)ln ;114)arctan ;5)arcsin ;6)cos sin ;17)sin cos ;8)sec tan ;9)csc cot ;cos sin 10)sec tan sec x dxkdx kx C x dx C x C xdx x C x C xdx x C x dx dx xdx x C xdx x C xdx x C x xx xdx x μμμμ+=+=+≠-=++=+=+=++=-+==+==-+=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰;11)csc cot csc ;12);13).ln x x x xa C x xdx x C e dx e C a dx C a+=-+=+=+⎰⎰⎰()();df x dx f x dx =⎰()() ;d f x dx f x dx =⎰[] ();dF(x) dx F x C dx =+⎰()() C dF x dx F x =+⎰二、定积分 1. 定积分的定义 由曲边梯形的面积导入:定义:设函数()f x 在[,]a b 上有界,在[,]a b 中任意插入若干个分点0121n n a x x x x x b -=<<<<<=L ,把区间 [,]a b 分成个n 小区间 01121[,],[,],,[,]n n x x x x x x -L ,各个小区间的长度依次为1102211,,,n n n x x x x x x x x x -∆=-∆=-∆=-L .在每个小区间 1[,]i i x x -上任取一点i ξ(1i i i x x ξ-≤≤),作函数值()i f ξ与小区间长度i x ∆的乘积()i i f x ξ∆(1,2,,i n =L ),并作出和1()(1)ni i i S f x ξ==∆∑L L记12max{,,,}n x x x λ=∆∆∆L ,如果不论对 [,]a b 怎样划分,也不论在小区间1[,]i i x x -上点i ξ怎样选取,只要当0λ→时,和S 总趋于确定的极限I ,那么称这个极限I 为函数()f x 在区间 [,]a b 上的定积分(简称积分),记作()ba f x dx ⎰,即1()lim ()nbi i ai f x dx I f x λξ→===∆∑⎰,其中()f x 叫做被积函数,()f x dx 叫做被积表达式,x 叫做积分变量,a 叫做积分下限,b 叫做积分上限,[,]a b 叫做积分区间.利用""εδ-的说法,上诉定积分的定义可以表述如下:设有常数I ,如果对于任意给定的正数0ε>,总存在一个正数δ,使得对于区间[,]a b 的任意分法,不论点i ξ在1[,]i i x x -上怎样选取,只要λδ<时,总有1()ni i i f x I ξε=∆-<∑成立,则称I 是()f x 在区间[,]a b 上的定积分,记作()ba f x dx ⎰.注意:a) 定积分要求积分区间有限,被积函数在积分区间上有界. b) 积分值与积分变量无关,即()()()b b ba a a f x dx f t dt f u du ==⎰⎰⎰. c) 在几何意义上,定积分表示的是函数图像与x 轴围成的代数面积. 例2. 函数的可积性必要条件:()f x 在[,]a b 上可积,则()f x 在[,]a b 上有界. 充分条件:a) ()f x 在区间[,]a b 上连续.b) ()f x 在[,]a b 上有界且只有有限个间断点.3. 定积分的性质约定a):当a b =时,()0ba f x dx =⎰ 约定b):当ab >时,()()baa b f x dx f x dx =-⎰⎰ 1) 线性性质:[()g()]()()bb baaakf x l x dx k f x dx l f x dx ±=±⎰⎰⎰2) 区间可加性:()()()bcba a c f x dx f x dx f x dx =+⎰⎰⎰ (c 为任意的常数) 3) 比较定理:如果在区间[,]ab 上,()0f x ≥,则()0ba f x dx ≥⎰ (ab <) 特别地,如果在区间[,]a b 上,()()f x g x ≥,则()()bba a f x dx g x dx ≥⎰⎰ (ab <) 推论:()()b ba a f x dx f x dx ≤⎰⎰ (ab <) (证明?) 4) 积分估值定理:在区间[,]a b 上,设 ()m f x M ≤≤, 则()()()ba mb a f x dx M b a -≤≤-⎰ (证明?)5) 积分第一中值定理:如果函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b ξ∈,使得()()()ba f x dx fb a ξ=-⎰ (证明?)推广形式:若()f x 与()g x 都在[,]a b 上连续,且()g x 在[,]a b 上不变号,则至少存在一点[,]a b ξ∈,使得()()()()bba a f x g x dx f g x dx ξ=⎰⎰ (证明?) 6)1badx b a =-⎰;设函数()f x 在[,]a b 上连续,非负,且()0ba f x dx =⎰,则()0f x ≡.例1 求极限1lim n x →∞⎰4. 变限积分定义:如果函数()f x 在[,]a b 上连续,则积分上限的函数 ()()xa x f t dt Φ=⎰在上可导,并且它的导数()()()xad x f t dt f x dx 'Φ==⎰ (a x b ≤≤) 注意:如果函数()f x 在[,]a b 上连续,则函数 ()()xa x f t dt Φ=⎰就是()f x 在[,]a b 上的一个原函数. (即连续函数必有原函数)a) 连续性:若()f x 在[,]a b 上可积,则()xa f t dt ⎰在[,]ab 上连续. b) 可导性:若()f x 在[,]a b 上连续,则()xa f t dt ⎰在[,]ab 上可导,且(())()xa f t dt f x '=⎰c) 变限积分求导法则:()()(())(())()(())()x x f t dt f x x f x x ψϕψψϕϕ'''=-⎰ d) 奇偶性:i) 若()f x 为连续奇函数,则0()xf t dt ⎰为偶函数;(证明?) ii)若()f x 为连续偶函数,则0()x f t dt ⎰为奇函数. 例 设()f x 在[,]a b 上连续,单调增.求证:()()2b ba a ab xf x dx f x dx +≥⎰⎰5. 微积分学基本定理——牛顿、莱布尼茨公式 如果函数()F x 是连续函数()f x 在[,]a b 上的一个原函数,则()()()baf x dx F b F a =-⎰例 1 设()f x 在[0,)+∞内连续且()0f x >.证明函数00()()()xx tf t dt F x f t dt=⎰⎰在(0,)+∞内为单调增加函数.例2 求 21cos 2limt xx e dt x-→⎰第二节 积分法则1. 第一类换元法(凑微分法) 常见的几类凑微分法:1()()()f ax b dx f ax b d ax b a +=++⎰⎰;11()()n n n nf x x dx f x dx n-=⎰⎰; 111()()n n n n f x dx f x dx x n x=⎰⎰;(sin )cos (sin )sin f x xdx f x d x =⎰⎰;(cos )sin (cos )cos f x xdx f x d x =-⎰⎰;2(tan )sec (tan )tan f x xdx f x d x =⎰⎰;()()x x x x f e e dx f e de =⎰⎰;1(ln )(ln )(ln )f x dx f x d x x=⎰⎰;()()ln ()()()f x df x dx f x C f x f x '==+⎰⎰. 例1 91dx x x +⎰2. 第二类换元法(变量替换法) 1)()1()[()]()()(())x t f x dxf t t dt F t C F x C ϕϕϕϕ=-'==+=+⎰⎰;2) 假设函数()f x 在[,]a b 上连续,函数()x t ϕ=满足条件: a) ()a ϕα=,()b ϕβ=;b) ()t ϕ在[,]αβ(或[,]βα)上具有连续导数,且其值域[,]R a b ϕ⊂,则有()[()]()baf x dx f t t dt βαϕϕ'=⎰⎰3) 常见的三角代换公式:a) sin (cos )x a t a t =令; b) tan x a t =令;c) sec x a t =令.3. 分部积分法——适用于两类函数的乘积形式的积分 1) udv uv vdu =-⎰⎰; 2) bbaab udv uvvdu a =-⎰⎰ 常见的分部法则:a) ()x n p x e dx α⎰;()sin n p x xdx α⎰;()cos n p x xdx α⎰. 将多项式以外的凑到d 上;b) ()ln n p x xdx ⎰;()arctan n p x xdx ⎰;()arcsin n p x xdx ⎰. 将多项式凑到d 上; c) sin x e xdx αβ⎰;cos x e xdx αβ⎰. 凑谁到d 上都可以,关键会算两步. 例1= 例2 =。
考研数学一高数下册范围

考研数学一高数下册范围答:第九章多元函数微分学及应用考试范围:1、两元函数极限的概念、存在性、求法与连续2、偏导数的定义与偏导数的求法及二阶偏导数3、二元函数可微分的判定及全微分的求法4、隐函数存在定理、求导方法及多元复合函数求导法则5、多元函数微分学的几何应用及方向导数与梯度(数一考试内容)6、多元函数的极值及其求法习题范围习题9-1:第2题、第6、7题习题9-2:第1题、第3题、第4题、第6题、第7题、第8、9题、习题9-3:第1题、第2题、第4题、第5题、习题9-4:第1、2、3、4题、第7题、第8、9、10题、第11题、第12、13题习题9-5:第1、3、4题、第5题、第6题、第7题、第8题、第9题、第11题习题9-6 (数学一考试内容):第4、5题、第6题、第7、8、9题第12题习题9-7 (数学一):第1、2题、第3题、第5、6题、第8题习题9-8:第1题、第2、3、4题、第11题总复习题九:第1题,第2题(数一)、第3题、第5题、第6题、第8题、第9题、第10题、第11题、第12题,第14、15、17题(数一) 第19题(数三),第20题(数一数二)第十章重积分(数二、三只考二重积分) .考试范围:1、二重积分的定义域性质2、二重积分的交换积分次序及二重积分的计算3、三重积分的性质、应用与三重积分的计算(数一考试内容)习题范围:刃題10-1:第4題、第5題可題10-2:第1題、第2題、第4、5題、第6題、第11、12題第13、14、、15題、第21題刃題10-3: (数学一考武内容)第1題、第4、5、6、7、8題、第9、10題第11、15題刃題10-4:第1、2題、第5題、第8題、第9題、第10、11題、第12、13題(数学一)忌ヲ題十:第1題、第2題、第3題、第4題、第5、6題第7題、第8題、第9題、第13題第十一章曲銭釈分与曲面釈分(数一)略第十ニ章无劣級数(数二不考)考武范国:1、常数級数的性貭与收斂性的判定(正項級数与交錯級数)2、冪級数的收斂区域与收斂半径的求法;3、函数展开成幂级数与幂级数和函数的求法4、傅里叶级数与三角级数、正弦余弦级数(数一考试内容)习题范围:习题12-1:第3题、第4题习题12-2:第1题、第2题、第3、4、5题习题12-3:第1题、第2题习题12-4:第3、4、5、6题习题12-7 (数一)第1题、第2题、第4题、第5题、题6题总习题十二:第1题、第2题、第3题、第5、6、7、8、9题第10题。
考研高数二考试大纲
考研高数二考试大纲考研高数二考试大纲是针对中国研究生入学考试数学科目的指导性文件,它规定了考试的范围、内容和要求。
以下是考研高数二考试大纲的主要内容:一、考试目标考研高数二旨在测试考生对高等数学的基本概念、基本原理和基本方法的掌握程度,以及运用这些知识解决实际问题的能力。
二、考试内容1. 函数、极限与连续性- 函数的概念、性质- 极限的定义、性质和运算- 无穷小的比较- 函数的连续性与间断点2. 导数与微分- 导数的定义、几何意义和物理意义- 基本导数公式- 高阶导数- 隐函数和参数方程的导数- 微分的概念和运算3. 中值定理与导数的应用- 罗尔定理、拉格朗日中值定理和柯西中值定理- 洛必达法则- 泰勒公式- 导数在几何、物理和经济中的应用4. 不定积分- 不定积分的概念和性质- 换元积分法和分部积分法- 有理函数和三角函数的积分5. 定积分及其应用- 定积分的定义和性质- 定积分的计算方法- 定积分在几何、物理和概率统计中的应用6. 多元函数微分法- 偏导数和全微分- 多元函数的极值问题- 方向导数和梯度7. 重积分- 二重积分和三重积分的概念和性质- 重积分的计算方法- 重积分在几何和物理中的应用8. 曲线积分与曲面积分- 第一类和第二类曲线积分- 格林公式、高斯公式和斯托克斯公式- 曲面积分的概念和计算方法9. 无穷级数- 常数项级数的收敛性- 幂级数和泰勒级数- 函数的傅里叶级数三、考试形式与题型考试形式为闭卷笔试,题型包括选择题、填空题、计算题、证明题和应用题等。
四、考试要求1. 理解并能熟练运用高等数学的基本概念、原理和方法。
2. 能够运用数学知识解决实际问题,具备一定的数学建模能力。
3. 掌握数学运算的基本技巧,能够准确、快速地进行数学计算。
4. 具备良好的逻辑推理能力和抽象思维能力。
五、复习建议1. 系统复习高等数学的基础知识,注重概念的理解与记忆。
2. 大量练习各类题型,提高解题速度和准确率。
2023考研高数数学一考试大纲
2023考研高数数学一考试大纲2023考研高数数学一考试大纲相关参考内容:第一部分:数列和数学归纳法数列:1. 数列的定义与性质,如等差数列、等比数列等;2. 求解数列的通项公式以及根据数列的通项公式计算数列的和;3. 数列的极限概念,极限存在的判定条件;4. 数列的极限性质,如夹逼定理、最值定理等。
数学归纳法:1. 数学归纳法的基本思想和步骤;2. 数学归纳法的证明方法和技巧;3. 利用数学归纳法证明数学命题的正确性。
第二部分:函数与极限函数:1. 函数的定义与性质,如奇偶性、周期性等;2. 常见初等函数的性质,如幂函数、指数函数、对数函数、三角函数等;3. 复合函数的概念和性质,链式法则的应用;4. 反函数的概念和性质,求解反函数的方法。
极限:1. 函数极限的定义与性质,极限存在与不存在的判定条件;2. 无穷小与无穷大的概念及其性质;3. 极限计算方法,如夹逼定理、洛必达法则、泰勒展开等;4. 函数的连续性概念及其判定条件。
第三部分:导数与微分导数:1. 导数的定义与性质,如可导性、连续性等;2. 常用函数的导数公式和性质,如幂函数的导函数、指数函数的导函数、对数函数的导函数等;3. 高阶导数的概念和应用;4. 参数方程的导数计算,隐函数的导数计算。
微分:1. 微分的概念与性质,微分的几何意义;2. 微分中值定理及其应用;3. 泰勒公式及其应用;4. 极值问题的求解,如最大值、最小值的判定条件等。
第四部分:定积分与不定积分定积分:1. 定积分的概念与性质;2. 定积分的计算方法,如换元法、分部积分法等;3. 定积分的应用,如曲线长度、曲线面积、体积等。
不定积分:1. 不定积分的概念与性质;2. 基本积分表及运算法则;3. 特殊函数的不定积分,如三角函数的不定积分、指数函数的不定积分等;4. 定积分与不定积分的关系。
以上是2023考研高数数学一考试大纲的相关参考内容,涵盖了数列和数学归纳法、函数与极限、导数与微分以及定积分与不定积分等内容,希望对您的学习有所帮助。
2024考研高数三大纲
2024年考研数学三大纲一、考试性质数学三是全国硕士研究生招生考试的重要组成部分,考查考生对基础数学知识的理解和应用能力。
考试要求考生具备扎实的数学基础,能够运用数学知识解决实际问题,并具备一定的创新能力和数学素养。
二、考试内容1. 函数、极限、连续:考查函数的基本性质、极限的计算、连续函数的性质等。
2. 一元函数微分学:考查导数的概念、导数的计算、微分中值定理等。
3. 一元函数积分学:考查不定积分、定积分的概念和计算、积分的应用等。
4. 多元函数微分学:考查多元函数的导数、偏导数的概念和计算,以及多元函数极值和最值的求解。
5. 多元函数积分学:考查二重积分、三重积分的概念和计算,以及曲线和曲面积分的求解。
6. 常微分方程:考查常微分方程的基本概念、一阶和二阶常微分方程的求解方法,以及常微分方程的应用。
7. 无穷级数:考查数项级数、幂级数的概念和性质,以及幂级数的展开等。
8. 随机事件和概率:考查随机事件的关系和运算、概率的定义和性质,以及古典概型和几何概型的概率计算。
9. 数理统计初步:考查数理统计的基本概念、参数估计和假设检验的方法等。
三、考试要求1. 理解数学基础知识,能够正确运用数学知识解决实际问题。
2. 掌握基本的数学方法,包括抽象思维、逻辑推理、空间想象等。
3. 具备创新能力和数学素养,能够运用数学知识进行数据处理、统计分析等。
四、考试形式和试卷结构1. 考试形式:数学三考试时间为180分钟,满分为150分。
考试形式为闭卷、笔试。
2. 试卷结构:试卷由选择题、填空题和解答题三种题型组成。
选择题和填空题分值占40%,解答题分值占60%。
3. 难易程度:试卷难度分为容易、较易、中等和较难四个等级。
容易题占30%,较易题占30%,中等题占20%,较难题占20%。
考研高数讲解新高等数学上册辅导讲解第一章上课资料
第一章函数与极限第 1 页第一节映射与函数一、集合常用数集:自然数集:整数集:有理数集:实数集:开区间:闭区间:半开区间:;邻域:去心邻域:二、函数定义:都有唯一与之对应,记为。
三、函数性质讨论函数:,讨论区间:1、有界性有界:假设,使得,称在区间上有界无界:对,总,使得,那么称在区间上无界上界、下界:假设,使得,,称在区间上有上界;假设,使得,,称在区间上有下界定理:假设在区间上有界在区间上有上界也有下界。
2、单调性严格单调增〔减〕:假设,且,恒有广义单调增〔减〕:假设,恒有,3、奇偶性偶函数:奇函数:常见奇函数:等常见偶函数:等4、周期性周期函数:,对,有,且,那么称为周期为周期函数。
常见周期函数:等【例1】〔87二〕是〔〕(A)有界函数. 〔B〕单调函数.〔C〕周期函数. 〔D〕偶函数.四、复合函数与反函数1、复合函数设定义域为,定义域为,值域为,且,在定义域上有复合函数。
【例2】〔88一二〕,且,求并写出它定义域.2、反函数将函数称为直接函数,函数称为反函数。
与图形关于直线对称。
五、初等函数第二节数列与函数极限一、数列极限定义数列:,,称为整标函数。
其函数值:叫做数列〔序列〕。
数列每一个数称为项,第项称为数列一般项。
简记数列为数列极限:已给数列与常数,如果对于,都,使得对于,不等式恒成立,那么称当时,以为极限,或收敛于,记为或。
反之,假设无极限,说发散。
二、函数极限定义〔1〕:设函数在内有定义,为一常数,假设对于,都,使有,那么称当时,以为极限,记为或。
单侧极限:左极限:。
右极限:定理:〔2〕:设函数在充分大时有定义,为一常数,假设对于,都,使都有,那么称当时,以为极限,记为或。
单侧极限:;定理:【例1】设〔为常数〕,求值,使得存在。
三、极限性质性质1 〔极限唯一性〕数列——假设存在,那么极限值是唯一。
函数——假设存在,那么其极限值是唯一。
性质2 〔有界性〕数列——如果收敛,那么一定有界。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考研数学一之高数复习计划名师指导数一高数学习计划数学复习具有基础性和长期性的特点,数学知识的学习是一个长期积累的过程,要遵循由浅入深的原则,先将知识基础打牢,构建起知识体系,然后再去追求技巧以及方法,一座高楼大厦必定是建立在坚实的地基之上的,因此我们将基础知识的复习安排在第一阶段,希望大家给予足够重视。
同时,有一个科学的学习计划,才能更迅速有效地掌握数学知识。
我们按照这个原则制定了详尽的数学学习计划,使得同学们能够迅速的巩固基础知识,循序渐进,加快数学学习的步伐,为今后数学水平的提高打下一个坚实的基础。
在研究生(论坛) 考试过程中先人一步,胜人一筹。
一、数学一试卷结构此试卷结构参考09年考研(论坛) 大纲种类内容比例题型比例数学一高等数学约56%线性代数约22%概率论与数理统计约22%填空题与选择题约37%解答题(包括证明题)约63%二、数学复习全年规划第一阶段夯实基础,全面复习主要目标:基本教材阶段。
吃透考研大纲的要求,做到准确定位,事无巨细地对大纲涉及到的知识点进行地毯式的复习,夯实基础,训练数学思维,掌握一些基本题型的解题思路和技巧,为下一个阶段的题型突破做好准备。
第二阶段熟悉题型,前后贯通主要目标:复习全书阶段。
大量习题训练,熟悉考研题型,加强知识点的前后联系,分清重难点,让复习周期尽量缩短,把握整体的知识体系,熟练掌握定理公式和解题技巧。
第三阶段查缺补漏,模拟训练主要目标:套题、模拟训练题阶段。
练习答题规范,保持卷面整洁,增加信心,练习掌握考试时间的分配,增强临场应变的能力,要对自己前两个阶段复习中出现含糊不清,掌握不牢的地方重点加强。
第四阶段强化记忆,保持状态主要目标:查漏补缺,回归教材。
强化记忆,调整心态,保持状态,积极应考。
三、教材的选择《高等数学》同济版:讲解比较细致,例题难度适中,涉及内容广泛,是现在高校中采用比较广泛的教材,配套的辅导教材也很多。
《线性代数》清华版:讲解详实,细致深入,适合时间充裕的同学(推荐)。
《线性代数》同济版:轻薄短小,简明易懂,适合基础不好的同学。
《概率论与数理统计》浙大版:课后习题中基本的题型都有覆盖。
四、学习方法解读(1)强调学习而不是复习对于大部分同学而言,由于高等数学学习的时间比较早,而且原来学习所针对的难度并不是很大,又加上遗忘,现在数学知识恐怕已经所剩无几了,所以,这一遍强调学习,要拿出重新学习的劲头亲自动手去做,去思考。
(2)复习顺序的选择问题我们建议先高等数学再线性代数再概率论与数理统计。
高等数学是线性代数和概率论与数理统计的基础,一定要先学习。
我们并不主张三门课齐头并进,毕竟三门课有所区别,要学一门就先学精了再继续推进,做成“夹生饭”会让你有种骑虎难下的感觉,到时你反而会耗费更多的时间去收拾烂摊子。
同学们也可根据自己的特殊情况调整复习顺序。
(3)注意基本概念、基本方法和基本定理的复习掌握结合考研辅导书和大纲,先吃透基本概念、基本方法和基本定理,只有对基本概念深入理解,对基本定理和公式牢牢记住,才能找到解题的突破口和切入点。
分析表明,考生失分的一个重要原因就是对基本概念、基本定理理解不准确,基本解题方法没有掌握。
因此,首轮复习必须在掌握和理解数学基本概念、基本定理、重要的数学原理、重要的数学结论等数学基本要素上下足工夫,如果这个基础打不牢,其他一切都是空中楼阁。
(4)加强练习,重视总结、归纳解题思路、方法和技巧数学考试的所有任务就是解题,而基本概念、公式、结论等也只有在反复练习中才能真正理解和巩固。
试题千变万化,但其知识结构却基本相同,题型也相对固定,一般存在相应的解题规律。
通过大量的训练可以切实提高数学的解题能力,做到面对任何试题都能有条不紊地分析和计算。
(5)不要依赖答案学习的过程中一定要力求全部理解和掌握知识点,做题的过程中先不要看答案,如果题目确实做不出来,可以先看答案,看明白之后再抛弃答案自己把题目独立地做一遍。
不要以为看明白了就会了,只有自己真正做一遍,印象才能深刻。
(6)强调积极主动地亲自参与,并整理出笔记注意一定要在学习过程中写出自己的感受,可以在书上以题注的形式或者就是做笔记,尽量深挖例题内涵,这一点很重要,并且要贯彻前三轮的复习,如果最后一轮复习我们有了自己整理的笔记,就会很轻松。
有同学说学习线性代数最好的办法就是亲自推导,这话很有道理,事实上如果我们学习什么知识都采取这种态度的话,那肯定都会学得非常好。
五、复习进度表每天至少应该花2.5-3.5个小时左右来复习数学,这样才能保证在基础阶段把整个数学的基础知识复习完。
其中用1.5-2个小时左右的时间理解掌握概念、定义等,用1-1.5小时左右来做习题巩固。
对于数学基础较薄弱的同学建议每天再加一个小时的复习时间用来做习题并总结。
具体每章复习所用的时间我们在每章题目旁边给出了一个复习时间限定期限,如果超出这个时间,或者少于这个时间最好要和你的主管顾问讲明原因,由主管顾问根据你学习的情况来调整复习的时间与内容。
注意:本计划对应习题涵盖在以下教材中:《高等数学》第五版同济大学应用数学系主编高等教育出版社《线性代数》第二版居余马编著清华大学出版社《概率论与数理统计》第三版浙江大学编著高等教育出版社复习计划使用说明:(1) 学习计划里有日期、学习时间,日期是对本章知识内容的限定时间,学习时间是针对复习知识点在大纲中的要求而建议应该使用的学习时间,同学们在学习的时候一定要两者同时兼顾,平时如果学习时间不够,可利用周末的时间做调整。
(2) 计划里明确了每章该看的知识点、该做的习题,后面备有大纲要求,学员要根据大纲要求合理学习知识点。
(3) 每章复习结束后都必须做单元测试题,单元测试题是准确把握学员是否按照大纲要求掌握了本章内容。
学员在做复习完每章内容后,跟主管顾问要本章测试题。
测试题做完后一定要把成绩反馈给你的主管顾问,以便主管顾问和教研组老师根据你的复习情况及时调整你的学习方法与内容。
(4) 同学们在复习的时候一定要和你周围的同学、老师多交流学习心得。
只有你总结出来的方法才是最适合你的方法。
(5) 同学们在复习的过程中肯定要遇到一些疑难问题、做错的题目,一定要在第一时间把他整理到你的笔记本里,方便的时候可以答疑。
高等数学第一章函数与极限(7天)微积分中研究的对象是函数。
函数概念的实质是变量之间确定的对应关系。
极限是微积分的理论基础,研究函数实质上是研究各种类型极限。
无穷小就是极限为零的变量,极限方法的重要部分是无穷小分析,或说无穷小阶的估计与分析。
我们研究的对象是连续函数或除若干点外是连续的函数。
日期学习时间复习知识点与对应习题大纲要求第一周2.5-3.5小时函数的概念,常见的函数(有界函数、奇函数与偶函数、单调函数、周期函数)、复合函数、反函数、初等函数具体概念和形式. 习题1-1:4,5,7,8,9,13,15,181.理解函数的概念,掌握函数的表示法,并会建立应用问题中的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念,以及函数极限存在与左、右极限之间的关2.5-3.5小时数列定义,数列极限的性质(唯一性、有界性、保号性 ) P26(例1,例2)P27(例3)习题1-2:1,3,4,5,62.5-3.5小时函数极限的基本性质(不等式性质、极限的保号性、极限的唯一性、函数极限的函数局部有界性,函数极限与数列极限的关系等)P33(例4,例5)P35(例7)习题1-3:1,2,4,6,7,82.5-3.5小时无穷小与无穷大的定义,它们之间的关系,以及与极限的关系习题1-4:1,2,4,5,6,72.5-3.5小时极限的运算法则(6个定理以及一些推论)P46(例3,例4),P47(例6),习题1-5:1,2,32.5-3.5小时两个重要极限(要牢记在心,要注意极限成立的条件,不要混淆,应熟悉等价表达式),函数极限的存在问题(夹逼定理、单调有界数列必有极限),利用函数极限求数列极限,利用夹逼法则求极限,求递归数列的极限P51(例1)习题1-6:1,2,42.5-3.5无穷小阶的概念(同阶无穷小、等价无穷小、小时高阶无穷小、k阶无穷小),重要的等价无穷小(尤其重要,一定要烂熟于心)以及它们的重要性质和确定方法 P57(例1)P58(例5)习题1-7:1,2,3,4 系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.2.5-3.5小时函数的连续性,间断点的定义与分类(第一类间断点与第二类间断点),判断函数的连续性(连续性的四则运算法则,复合函数的连续性,反函数的连续性)和间断点的类型。
例1-例5习题1-8:2,3,4,52.5-3.5小时连续函数的运算与初等函数的连续性(包括和,差,积,商的连续性,反函数与复合函数的连续性,初等函数的连续性) 例4-例8 习题1-9:1,2,3,4,52.5-3小时理解闭区间上连续函数的性质:有界性与最大值最小值定理,零点定理与介值定理(零点定理对于证明根的存在是非常重要的一种方法). 例1-例2,习题1-10:1,2,3,4,53.5小时总复习题一:1,2,8,9,10,11,122小时本章测试题-检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格继续向前复习,如果不合格总结自己的薄弱点还要针对性的对本章的内容进行复习或者到总部答疑。
第二章:导数与微分(6天)一元函数的导数是一类特殊的函数极限,在几何上函数的导数即曲线的切线的斜率,在力学上路程函数的导数就是速度,导数有鲜明的力学意义和几何意义以及物理意义。
函数的可微性是函数增量和自变量增量之间关系的另一种表达形式。
函数微分是函数增量的线性主要部分。
日期学习时间复习知识点与对应习题大纲要求第二周2.5-3.5小时导数的定义、几何意义、力学意义,单侧与双侧可导的关系,可导与连续之间的关系(非常重要,经常会出现在选择题中),函数的可导性,导函数,奇偶函数与周期函数的导数的性质,按照定义求导及其适用的情形,利用导数定义求极限. 会求平面曲线的切线方程和法1. 理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和线方程. 例3-例7 习题2-1:6,7,9,11,14,15,16,17 法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系. 2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分. 3.了解高阶导数的概念,会求简单函数的高阶导数. 4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数. 2.5-3.5小时复合函数求导法、求初等函数的导数和多层复合函数的导数,由复合函数求导法则导出的微分法则,(幂、指数函数求导法,反函数求导法),分段函数求导法 例-例17 习题2-2:2,3,4,7,8,9,1012) 2.5-3.5小时高阶导数和N 阶导数的求法(归纳法,分解法,用莱布尼兹法则) 例1-例7 习题2-3:2,3,4,7,8,9 2.5-3.5小时由参数方程确定的函数的求导法,变限积分的求导法,隐函数的求导法 例1-例10 习题2-4:2,4,7,8,9,11 2.5-3.5小时函数微分的定义,微分运算法则,一元函数微分学的简单应用 例1-例6 习题2-5:1,2,3,4,5,6, 2.5-3.5小时总复习题二:1,2,3,5,6,9,11,13 2小时 第二章测试题 检验自己是否对本章的复习合格(合格成绩为80分以上),如果合格继续向前复习,如果不合格总结自己的薄弱点还要针对性的对本章的内容进行复习或者到总部答疑。
