knn算法的基本原理
KNN算法及Java实现

maxIndex = i; maxCount = classCount.get(classes[i]); } } return classes[maxIndex].toString(); } }
package cqu.KNN;
import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.util.ArrayList; import java.util.List;
3.KNN 算法流程 1)准备数据,对数据进行预处理 2)选用合适的数据结构存储训练数据和测试元组
3)设定参数,如 k 4)维护一个大小为 k 的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选 取 k 个元组作为初始的最近邻元组,分别计算测试元组到这 k 个元组的距离,将训练元组标号和距离存入 优先级队列
新材料kNN算法在电力故障诊断中的应用

新材料kNN算法在电力故障诊断中的应用随着电力设备的普及使用,电力故障问题也变得愈发严重。
传统的电力故障诊断方法主要基于复杂的经验公式和人工判断,存在着主观性和误判率较高等问题。
然而,随着新材料kNN算法的出现,人们对于电力故障的诊断方法得到了重大突破。
本文将着重介绍新材料kNN算法的基本原理,以及在电力故障诊断中的应用。
一、什么是新材料kNN算法?kNN(k-Nearest Neighbor)算法是一种基于样本分类的算法,它的基本原理是将样本空间中最邻近的k个重合最多的样本定义为该样本所属的类别,从而实现对于新样本的分类。
新材料kNN算法是在传统kNN算法的基础上进行改进和优化,并结合了材料科学的相关理论和技术,能够更加准确地识别材料的种类和性质,并在电力故障诊断中有着广泛的应用。
二、新材料kNN算法的基本原理1. 样本空间定义新材料kNN算法的样本空间是由k个维度构成的,而这些维度定义了材料的各种性质。
例如在电力故障诊断中,样本空间的维度可以包括电压、电流、功率、频率等等。
2. 样本空间中近邻的定义在新材料kNN算法中,样本空间中近邻的定义是基于一种距离度量方法的。
而距离的度量方法可以通过欧氏距离、曼哈顿距离等算法实现。
这些算法都可以通过计算样本间的距离,从而找到距离被分类样本最近的k个训练样本。
3. 评估新样本所属类别一旦找到了距离被分类样本最近的k个训练样本,就可以通过统计这k个训练样本的分类结果,来决定被分类样本所属的类别。
在新材料kNN算法中,类别的统计总是建立在训练样本中与被分类样本相似性的基础上。
三、新材料kNN算法在电力故障诊断中的应用新材料kNN算法是一种非常有效的电力故障诊断方法,它可以通过对电力设备的各种性质进行快速而准确的分类,并通过对分类结果的统计分析,得出电力设备被损坏的可能性。
新材料kNN算法的应用主要包括以下几个方面:1. 电力设备状态监测通过对电力设备各种性质的监测,新材料kNN算法可以及时发现设备的故障状态,并根据其分类结果,对故障的严重程度进行快速的评估。
knn算法的基本要素

knn算法的基本要素KNN算法的基本要素KNN算法是一种非常常见的机器学习算法,它可以用于分类和回归问题。
在这篇文章中,我们将介绍KNN算法的基本要素,包括什么是KNN算法、KNN算法的工作原理、如何选择k值、如何选择距离度量以及如何处理数据集中的缺失值。
什么是KNN算法?KNN(k-Nearest Neighbors)算法是一种基于实例的学习方法。
它通过找到与新数据点最近邻居进行预测。
在分类问题中,预测结果为新数据点所属类别中出现次数最多的类别;在回归问题中,预测结果为最近邻居的平均值或加权平均值。
KNN算法的工作原理KNN算法主要有以下三个步骤:1. 计算距离:对于每个测试样本,计算它与所有训练样本之间的距离。
2. 选择k值:根据距离从小到大排序后,选择前k个样本作为最近邻居。
3. 预测:对于分类问题,预测结果为前k个最近邻居中出现次数最多的类别;对于回归问题,预测结果为前k个最近邻居的平均值或加权平均值。
如何选择k值?选择k值是KNN算法中一个重要的问题。
如果k值太小,模型会过拟合;如果k值太大,模型会欠拟合。
通常情况下,我们可以使用交叉验证来选择最优的k值。
如何选择距离度量?在KNN算法中,距离度量是一个非常重要的因素。
常用的距离度量包括欧几里得距离、曼哈顿距离和闵可夫斯基距离等。
在实际应用中,我们需要根据具体问题来选择合适的距离度量。
如何处理数据集中的缺失值?在实际应用中,数据集中经常会存在缺失值。
对于KNN算法来说,我们可以使用以下两种方法来处理缺失值:1. 删除缺失样本:如果缺失样本占比较小,可以直接删除这些样本。
2. 填充缺失值:如果缺失样本占比较大,可以使用插补法(interpolation)或者估计法(estimation)来填充缺失值。
总结KNN算法是一种基于实例的学习方法,在分类和回归问题中都有广泛应用。
在使用KNN算法时,需要注意选择合适的k值和距离度量,同时需要处理数据集中的缺失值。
knn缺失值填补原理

knn缺失值填补原理KNN算法是一种基于最邻近的分类算法,在分类问题中得到了广泛应用。
但是,在实际运用场景中,经常会出现数据集中缺失数据的情况,这就需要对KNN算法进行缺失值填补。
本文将从KNN算法和缺失值的定义入手,详细介绍KNN缺失值填补的原理和方法。
一、KNN算法与缺失值KNN算法(K-Nearest Neighbor Algorithm)是一种监督学习算法,其基本思想是找到与未知数据样本最相似的K个数据样本,然后利用这些数据样本的类别进行决策。
KNN算法的主要优点在于它的简单性和易于实现性。
而缺失值是数据处理中常见的问题,是指数据集中的某些属性或值缺失的情况。
对于这些缺失数据的处理方法主要包括删除、插值和模型预测等方法。
其中,KNN缺失值填补就是一种插值方法。
二、KNN缺失值填补原理KNN算法模型基于与数据样本最相似的K个数据样本进行决策,而这个相似性是通过计算两个数据样本之间的距离(或相似度)来评估的。
因此,KNN缺失值填补的原理就是:用数据集中K个与当前缺失值最相似的数据样本来进行插值,计算这些数据样本在当前属性上的平均值或加权平均值来填补缺失值。
下面分步骤进行具体介绍:步骤一:计算距离首先,对于数据集中的每个数据样本,都需要计算其与当前缺失值之间的距离。
这个距离可以通过欧氏距离、曼哈顿距离、切比雪夫距离等多种距离测度方式进行计算,选择距离最短的K个数据样本。
步骤二:选择邻居在计算出K个最近的邻居后,将它们的当前属性值取平均值或加权平均值,作为缺失值的填补值。
加权平均值的权重可以按照距离的远近进行分配,即距离缺失值近的邻居权重更大,距离缺失值远的邻居权重更小。
步骤三:重复填补过程对于数据集中的每个缺失值,都需要重复上述过程进行填补,直到所有的缺失值都被填补完毕。
三、总结KNN算法作为一种重要的分类算法,在数据处理过程中经常遇到缺失值的问题。
KNN缺失值填补就是一种有效的插值方法,其原理是通过计算最近的邻居来确定缺失值的填补值,可以充分利用数据集中的有用信息来提高填补值的准确性。
knn 算法
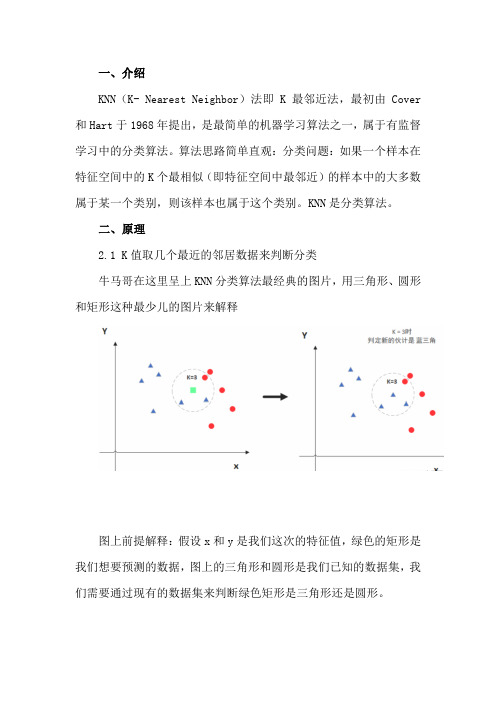
一、介绍KNN(K- Nearest Neighbor)法即K最邻近法,最初由 Cover 和Hart于1968年提出,是最简单的机器学习算法之一,属于有监督学习中的分类算法。
算法思路简单直观:分类问题:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN是分类算法。
二、原理2.1 K值取几个最近的邻居数据来判断分类牛马哥在这里呈上KNN分类算法最经典的图片,用三角形、圆形和矩形这种最少儿的图片来解释图上前提解释:假设x和y是我们这次的特征值,绿色的矩形是我们想要预测的数据,图上的三角形和圆形是我们已知的数据集,我们需要通过现有的数据集来判断绿色矩形是三角形还是圆形。
当K = 3,代表选择离绿色矩形最近的三个数据,发现三个数据中三角形比较多,所以矩形被分类为三角形当K = 5,代表选择离绿色矩形最近的三个数据,发现五个数据中圆形最多,所以矩形被分类为圆形所以K值很关键,同时建议k值选取奇数。
2.2 距离问题在上面的原理中还有一个关键问题,就是怎么判断距离是否最近。
在这里采用的是欧式距离计算法:下图是在二维的平面来计算的,可以当作是有两个特征值那如果遇到多特征值的时候,KNN算法也是用欧式距离,公式如下:从这里就能看出KNN的问题了,需要大量的存储空间来存放数据,在高维度(很多特征值输入)使用距离的度量算法,电脑得炸哈哈,就是极其影响性能(维数灾难)。
而且如果要预测的样本数据偏离,会导致分类失败。
优点也是有的,如数据没有假设,准确度高,对异常点不敏感;理论成熟,思想简单。
三.KNN特点KNN是一种非参的,惰性的算法模型。
什么是非参,什么是惰性呢?非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。
也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
机器学习--K近邻(KNN)算法的原理及优缺点

机器学习--K近邻(KNN)算法的原理及优缺点⼀、KNN算法原理 K近邻法(k-nearst neighbors,KNN)是⼀种很基本的机器学习⽅法。
它的基本思想是:在训练集中数据和标签已知的情况下,输⼊测试数据,将测试数据的特征与训练集中对应的特征进⾏相互⽐较,找到训练集中与之最为相似的前K个数据,则该测试数据对应的类别就是K个数据中出现次数最多的那个分类。
由于KNN⽅法主要靠周围有限的邻近的样本,⽽不是靠判别类域的⽅法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN⽅法较其他⽅法更为适合。
KNN算法不仅可以⽤于分类,还可以⽤于回归。
通过找出⼀个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
更有⽤的⽅法是将不同距离的邻居对该样本产⽣的影响给予不同的权值(weight),如权值与距离成反⽐。
KNN算法的描述: (1)计算测试数据与各个训练数据之间的距离; (2)按照距离的递增关系进⾏排序; (3)选取距离最⼩的K个点; (4)确定前K个点所在类别的出现频率 (5)返回前K个点中出现频率最⾼的类别作为测试数据的预测分类。
算法流程: (1)准备数据,对数据进⾏预处理。
(2)选⽤合适的数据结构存储训练数据和测试元组。
(3)设定参数,如k。
(4)维护⼀个⼤⼩为k的的按距离由⼤到⼩的优先级队列,⽤于存储最近邻训练元组。
随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存⼊优先级队列。
(5)遍历训练元组集,计算当前训练元组与测试。
元组的距离,将所得距离L 与优先级队列中的最⼤距离Lmax。
(6)进⾏⽐较。
若L>=Lmax,则舍弃该元组,遍历下⼀个元组。
若L < Lmax,删除优先级队列中最⼤距离的元组,将当前训练元组存⼊优先级队列。
(7)遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
KNN与SVM机器学习算法的比较研究

KNN与SVM机器学习算法的比较研究KNN与SVM机器学习算法的比较研究机器学习是目前最为热门的研究领域之一,其应用范围涵盖了许多领域,例如物流、金融、医疗等。
机器学习算法可以通过大量的数据分析和处理,然后利用统计学和数学模型来实现数据分类、预测和决策等功能。
K-近邻算法(KNN)和支持向量机(SVM)是机器学习算法中非常重要的两个算法,本文将从算法原理、应用场景和优缺点等方面对这两种机器学习算法进行详细的比较。
1.算法原理1.1 K-近邻算法K-近邻算法是一种基于实例学习的算法,即根据相似性度量确定一组最近邻居,然后基于这些最近邻的学习样本来进行分类。
该算法适用于小数据集,训练数据集每个样本都有标签,而测试数据没有标签。
当有新的测试数据时,该算法根据测试数据与训练数据的距离来判断该测试数据属于哪个类别,从而实现分类效果。
KNN算法的步骤如下:1)确定最近邻数K;2)计算测试数据与训练数据之间的距离,并按照距离的远近排序;3)选择距离最近的K个邻居;4)统计这K个邻居的类别,并将测试数据归类为这K个邻居中出现最多的类别。
1.2支持向量机支持向量机(SVM)是一种有监督学习算法,其基本思路是利用非线性变换将样本数据映射到高维空间,然后在高维空间中构建一个最优的线性分类器。
SVM算法可以有效地解决线性不可分的问题并具有很强的泛化能力。
SVM算法的主要流程如下:1)将数据集映射到高维空间;2)在高维空间中找到一个超平面,使得各类别之间的间隔最大;3)将新的数据映射到高维空间中,并进行分类。
2.应用场景KNN算法和SVM算法都被广泛应用于分类和回归问题。
2.1 K-近邻算法KNN算法的应用范围非常广泛,特别是在图像和语音识别以及医疗、金融和物流等领域。
例如,利用KNN算法可以对医疗图像进行分类,帮助医生进行疾病诊断。
同时,KNN算法也可以应用于推荐系统的开发,例如将用户的历史行为数据作为训练集,并根据相似性度量判断用户的兴趣爱好,从而向用户推荐内容。
knn算法原理

knn算法原理KNN(K近邻算法)是一种基于实例的机器学习算法,是机器学习领域中非常常见的算法。
KNN法的基本思想是:如果一个样本在特征空间中的k个最相近的样本中的大多数属于某一个类别,则该样本也属于该类别。
KNN法中,所选择的邻居都是已经正确分类的对象。
KNN法的基本原理是:在给定一个未知类别的对象(样本数据)时,根据其特征属性和它最接近的K个已经知道分类的样本,对这个对象进行分类。
KNN法就是从训练集中找出这K个“邻居”,根据这K 个“邻居”的类别,来确定当前未知类别的对象的分类。
KNN法的基本流程如下:1. 从训练集中计算测试实例与每个训练集实例之间的距离;2.据距离选择K个最近邻;3.据K个邻居的类别,通过投票或者加权求和,确定测试实例的类别。
KNN法使用数据中“靠近”的训练实例来预测未知实例,因此,KNN法是一种基于实例的学习算法。
KNN法的实质是在训练集中查找与当前输入实例最在的 K 个实例,并将它们的“类标记”作为对应的输入实例的预测。
KNN法的优点是:1. KNN法的思想简单,实现容易,它不需要学习过程,也不需要假设数据的分布,只需要保存所有数据实例;2.实际数据建模时,可以有效地处理属性间关系比较复杂和数据不平衡的情况;3. KNN法可以灵活地处理不同的数据类型。
KNN法也存在一些缺点:1. KNN法需要大量的计算,当训练数据集特别大的时候,搜索K 个最近邻计算量就比较大,可能会耗费较多的时间;2. KNN法的效果依赖于k的值,但是k的值没有一个理论上的确定方法,只能选取不同的k值进行实验;3. KNN法不能很好地处理类别不平衡问题,因为它采用的算法是加权求和,类别不平衡的情况下,加权求和会倾向于那些比较多的类别;4. KNN法的思想是当前的数据点的类别取决于它的K个邻居,而这里的K个邻居都是已经被正确分类的,即每个邻居都是“正确”的,这种认为是不合理的,因为它假定K个邻居的类别都被正确分类了,而这并不一定是真的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
knn算法的基本原理
knn算法是一种基于实例的学习算法,也被称为最近邻算法。
其基本原理是:给定一个测试样本,从训练数据集中找到与之最相似的k个样本,然后通过对这k 个样本的标签进行综合评价,来确定该测试样本的类别。
具体实现步骤如下:
1. 将训练样本和测试样本表示为向量。
2. 根据所采用的距离度量方法,计算测试样本与训练样本之间的距离。
3. 选出距离测试样本最近的k个训练样本。
4. 对这k个样本的标签进行统计分析,选出出现次数最多的标签作为测试样本的预测标签。
5. 输出测试样本的预测标签。
knn算法的关键在于距离的计算和k值的确定。
距离计算通常采用欧几里得距离、曼哈顿距离等。
k值的确定要根据数据集的特点和实际需求进行调整。
在k过小时,会产生过拟合的现象;而当k过大时,又会产生欠拟合的现象。
因此,k值的选择需要平衡过拟合和欠拟合之间的关系。
