第3章 分子的对称和群
分子的对称性与群论基础群与分子点群
群与分子点群
3、分子点群
立方群
3)、 Ih 点群
对称元素: 6个 C5 轴(相对顶点)、 10个 C3 轴(相对面心)、 15个 C2 轴(相对棱心)、 对称中心.
120个对称操作,分为10个共轭类:
Eˆ , 6 Cˆ5 ,Cˆ54 , 6 Cˆ52,Cˆ53 , 10 Cˆ3 , Cˆ32 , iˆ , 6 Sˆ10 , Sˆ190 , 6 Sˆ130 , Sˆ170 , 10 Sˆ6 , Sˆ65 ,
24
群与分子点群
4、子群与类
如果群的某个元素与其他元素的乘积都可交换,则该元素
自成一类(不与其他元素共轭)。
若:
PA = AP ,
PB =
BP , … ...
必有:
A-1PA = P , B-1PB =
P , …… 即:对元于素分子P 点不群与:其他元素共轭。 恒等操作自成一类; 反演操作自成一类。
O2 , CO2 , C2 H 2
13
群与分子点群
3、分子点群
立方群
具有多于一个高次轴(Cn,n>2)的群,对应于凸正 多面体
4个 C3 轴 3个 C2 轴
T
Th (i)
Td (6d)
正四面体
3个 C4 轴 4个 C3 轴 6个 C2 轴
O Oh (i)
正八面体 正六面体
6个 C5 轴 10个 C3 轴
27
群与分子点群
5、同构与同态
2)、同态 定义:考虑群G与群H,若G的一组元素对应与H的一个元 素,且群G的元素的乘积对应于群H的相应元素的乘积, 则称群H 是群G的一个同态映像。
群G: …., {Aik} , …, {Aj l }, …., {AikAjl} , ….
第三章:分子对称性和点群

σv2 σv2 σd1 σv1 σd2 C42 E
C41 C43
σd1 σd1 σv1 σd2 σv2 C41 C43 E
C42
σd2 σd2 σv2 σd1 σv1 C43 C41 C42 E
第三章:分子对称性和点群
1
群元素 群
乘法
对称操作 点群
操作动作的连续
2
本章目录
3.1对称元素和对称操作 3.2 对称操作的乘积 3.3分子点群
3.3.1 构成群 3.3.2 点群乘法表 3.3.3 类和子群 3.3.4 分子点群的类型 ****
3
3.1对称元素和对称操作
• 对称元素的定义(Symmetry Elements) 几何实体,如一个点,一条直线,一个平面;
(x,y,z) -C-2-(-x-)-> (x,-y,-z)-C--2(-y-)> (-x,-y,z) (x,y,z) -C--2(-z-)-> (-x,-y,z)
so, C2(y)C2(x)= C2(z)
34
例3:C4(z)和σ (xz)的存在,自动地要求σ d的存在 普通点[x1,y1,z1]通过xz平面的反映效果可以表为
分子点群满足数学群四准则。
点群中点的含义:(1)这些对称操作都是点操作,操作时 分子中至少有一点不动;(2) 分子的全部对称元素至少通 过一个公共点。
37
满足群的四点要求:
• (1)群中任意两个元素的乘积必为群中的 一个元素。
以NH3为例,逐一求出所有的对称操作的二元乘 积,发现两个操作的乘积仍为集合中的一个操作。
Snm = hmCnm (1)若独立地存在一个Cn轴和一个垂直于它 的平面h,那么就存在Sn。 (2)当分别地既不存在Cn也不存在垂直的h 时,Sn也可以存在。
分子对称性和群论初步

Cn轴产生n个旋转操作的周期均为n。
(2)对称轴 (Cn )和旋转操作 (Cn )
对称元素: 旋转轴C2 对称操作: 旋转
H2O中的C2
H2O2中的C2
NH3中的C3轴
SF6中的C4轴
Fe(C5H5)2中的C5轴
C6H6中的C6轴
N2中的C∞轴
(3)对称面 s 和反映操作 s
对称面
相当于一个镜面,把分子图形分成两个完全相等的对称 部分,两部分之间互为镜中映象;对称面所相应的对称 操作是镜面的一个反映,在对称面的反映操作下,分子 图形相等的两部分互相交换位置,相同性质的点(同类 原子)彼此置换。显然,反映操作的周期为2,即:
ˆ ˆ =E s
操作定义
Cn旋转轴能生成n个旋转操作,记为:
2 ˆ ˆ n, Cn , C
…
, ˆn=E ˆ C Cn
n 1 n
ˆk 若取逆时针方向的旋转为正操作,表示为 C n,则顺 k ˆ 时 针 旋 转 为 逆 操 作 , 表 示 为C n ,不难理 (nk )。 ˆk ˆ 解C n =C n
操作的周期
S8
2.5 假轴向群 Sn群
Sn:有一个 n重象转轴,须考虑 n的奇偶性。 n为偶数时, 群中有n个元素,n为奇数时,Sn不独立存在。 只有S4是独立的点群。例如:1,3,5,7-四甲基环辛四烯, 有一个S4映转轴,没有其它独立对称元素。
S2 S4
2.6 六方群
1). Td群
若一个四面体骨架的分子,存在4个C3轴,3个C2轴,同时每 个C2轴还处在两个互相垂直的平面sd的交线上,这两个平面还 平分另外2个C2轴(共有6个这样的平面)则该分子属Td对称性。 对称操作为{E,3C2,8C3,6S4,6sd}共有24阶。 四 面 体 CH4 、 CCl4 对 称 性 属 Td 群 , 一 些 含 氧 酸 根 SO42- 、 PO43-等亦是。在CH4分子中,每个C-H键方向存在1个C3轴,2 个氢原子连线中点与中心C原子间是C2轴,还有6个sd平面。
群论第3章

NH3
CO,NO,HCN
C3v
C∞v
③ Cnh 群 属于Cnh点群的分子中具有一个Cn轴和一个垂直于Cn轴的σh 对称元素:Cn和σh 因σhCn=Sn,故(n-1)个旋转必产生(n-1)个象转 实际上 Cnh群是Cn群和Cs群的直积,阶次为2n 。
Cnh Cn Cs E, Cn1 , Cn 2 ,..., Cn n1 E, h = E, Cn1 , Cn 2 ,..., Cn n1 , h , hCn1 Sn , hCn 2 ,..., hCn n1
第三章. 分子对称性与分子点群
3.1 分子对称性
利用对称性原理和概念探讨分子的结构和性质,是人们认 识分子的重要途径,是了解分子结构和性质的重要方法。 ① 能简明地表达分子的构型 Ni(CN)42-离子具有D4h点群的对称性,用D4h这个符号就可以 准确地表达 9 个原子在同一平面上, Ni 原子在中心位置, 周围4个-CN完全等同,Ni-C-N都是直线型,互为90°角。 ② 简化分子构型的测定工作
3.分子的对称操作和对称元素:
分子是有限物体,在进行对称操作时,分子中至少有一 点不动------点操作 只有四种类型的对称操作和对称元素 a. 旋转操作------旋转轴(Cn)
b. 反映操作------镜面( σ )
c. 反演操作------ 对称心(i) d. 象轴(旋转反映)操作------象转轴(反轴)Sn 右手坐标系:讨论对称操作时,常将分子定位在右手坐 标轴系上,分子的重心处在坐标原点,主轴与Z轴重合。 主轴:分子中轴次最高的轴。
Cnh 待 定 分 子 是 否 直 线 型 N Y i Td
例:有两个分子群 D2 { E,C2(x),C2(y),C2(z) }
第三章分子对称性和点群
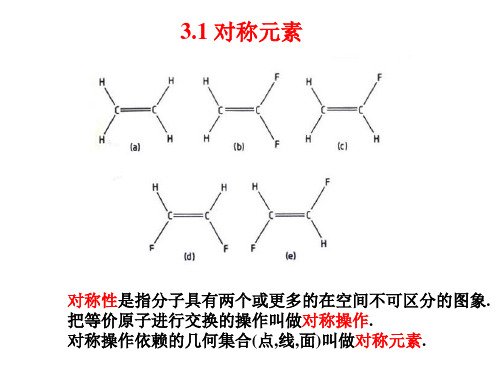
A(c) A(a) A( f ) 0 1
0
0
001
cos 4
3
sin 4
3 0
sin 4
3
cos 4
3 0
0 0Βιβλιοθήκη cos 43sin 4
3
1 0
sin 4
3
cos 4
3 0
0
0
1
A (a) 1
A (b) 1
A (c) 1
表示的分类:
(1)等价表示 若A(g)是群G的一个表示, X是一正交变换矩阵, 则 B(g)=X-1A(g)X
规则二. 点群中所有不可约表示的维数的平方和等于群的阶 n. l12 l22 lk 2 n
在 D3中, l12 l22 l32 6
从而 l1 l2 1, l3 2
规则三. 点群中不可约表示特征标间的正交关系:
k
h j r (R j ) * s (R j ) n rs
j 1
对不可约表示: (R) 2 n
3
y2 a21 a22 a23 x2 , yi aij x j
y3 a31 a32 a33 x3
j 1
(i=1,2,3)
矩阵的迹 (trace) 或特征标 (character):
( A) TrA aii
i
相似变换:
A S1AS
TrA TrA
(S为正交矩阵) St S SSt E
3.1 对称元素
对称性是指分子具有两个或更多的在空间不可区分的图象. 把等价原子进行交换的操作叫做对称操作. 对称操作依赖的几何集合(点,线,面)叫做对称元素.
3.1.1 n重对称轴, Cn (转动)
转角 2 / n
分子的对称和群
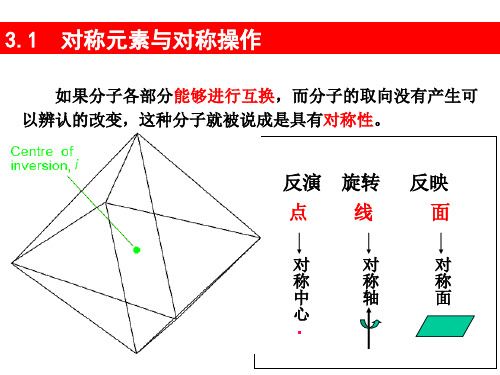
(正四面体构型的分子)
对称元素:3个C2,4个C3,3个S4 , 6个d
ˆ ,4C ˆ ,4C ˆ 2 ,3S ˆ1 ,3S ˆ 3 ,6 ˆ ,3C ˆd Td E 2 3 3 4 4
C3 C2 (S4)
24阶群
Cபைடு நூலகம்4
P4
d
CH4、P4、GeH4、SO42-、ClO4-、CrO4-、MnO4-
Cn
C2
阶数:2n
C2 C2
C2
D2
[Co(dien)2]3+
C2
D3
[Co(en)3]3+
2) Dnh群 对称元素: E,Cn,nC2,h, (nv, Sn) 阶数:4n
C2H4, N2O4 D2h
C6H6 D6h
重叠式C2H6
D3h
Cl Cl Re Re Cl Cl
Cl
Cl Cl Cl
Cl Cl Re Re Cl Cl
Cl
Cl Cl Cl
找出对称元素
PCl5
Mn(CO)5I
§3.2 点对称操作群(点群)
3.2.1 群的定义、群阶
3.2.2 主要点群
3.2.3 分子点群的确定
3.2.1 群的定义、群阶
我们称元素的某个集合形成一个群,群有着严格 的定义:“封闭性、结合律成立、存在恒等元素、存 在逆元素”。群中元素的个数,称作群阶。
C 6 H6
PtCl42
-
CO2
N2F2
SiF4
BF3
对称中心的性质
• 通过中心连续进行两次反演,分子中所有 原子均回到起始位置,得到起始构型的恒 等构型,其效应等于不动,即i2=E。由此 推得,i2n=i2=E; i2n+1=i, n为整数.
人教版高中选修(B版)3-44.3分子对称性群教学设计

人教版高中选修(B版)3-44.3分子对称性群教学设计一、教学目标了解分子的对称性及对称操作与对称元素的概念,掌握用对称操作的方法确定分子的对称性质及其对物理属性的影响。
二、教学内容及重点难点1. 教学内容1.对称元素和对称操作的概念2.分子的对称性3.分子对称性对物理属性的影响2. 重点难点对称操作和对称元素的理解、分子对称性的确定方法、分子对称性对物理属性的影响的理解。
三、教学过程1. 导入(10分钟)1.复习上一节课的知识:分子几何构型;2.导入今天的教学内容,并提出目标、重点和难点。
2. 讲授(40分钟)1.对称元素和对称操作的概念(20分钟)。
–分子中的对称轴、面、中心等概念;–对称元素是什么,对称操作是什么;–对称元素和对称操作的种类和区别。
2.分子的对称性(10分钟)。
–分子对称性的定义和性质;–根据对称性质判断分子的对称种类。
3.分子对称性对物理属性的影响(10分钟)。
–分子对称性和物理性质的关系;–分子对称性和光学活性的关系。
3. 练习(30分钟)1.练习题的课堂讲解(10分钟)。
2.学生自主研究分子对称性的分析题(20分钟)。
4. 小结(5分钟)总结本节课的主要内容和学习方法。
四、教学手段教师讲解、讨论、活动、课堂自主研究和个别辅导。
五、教学重点1.对称元素和对称操作的概念;2.分子的对称性;3.分子对称性对物理属性的影响。
六、教学难点分子对称性的确定方法。
七、教学亮点通过引入生动的例子和实验等形式,让学生深刻理解对称元素和对称操作的概念,并掌握分子对称性对物理属性的影响。
八、教学反思通过本节课的教学,让学生了解了分子的对称性及其对物理属性的影响。
在教学中,应该多引入生动的例子、实验等形式,让学生能够更好地理解和掌握知识。
同时,针对分子对称性的确定方法这一难点,可以引入更多的例子和练习,让学生能够更加自主地掌握该知识点。
分子的对称性和群论初步

H3BO3分
子
C3h C31, C32 , C33 E, h , S31, S35
属6阶群 S31 hC31,S32 C32,S33 h S34 C31,S35 hC32,S36 E
Cnh Cnk (k 1,n 1), E, h , hCnl (l 1,l 1)
非全同:不能通过平移或转动等第一类对称操 作使两个图形叠合。
2.旋光异构体:一对等同而非全同的分子构成 的一对对映体。
3.手性分子:没有第二类对称元素的分子。
R(右,顺时针方向转)和 S(左,逆时针旋转) 外消旋体:等量的R和S异构体混合物一定无旋光
性方向相反
4.对称性和旋光性的关系
✓ 若分子具有反轴Ι(先旋转360°/n,再反演)的对 称性,一定无旋光性;若分子不具有反轴的对称性, 则可能出现旋光性。
元的数目有限的群称为有限群,数目无限的群 称为无限群。
点群:一个有限分子的对称操作群 ☞“点”的含义 ✔这些对称操作都是点操作,操作时分子中至少
有一个点不动。 ✔分子的对称元素至少通过一个公共点。
2.2 群的乘法表
※顺序
乘法表由行和列组成,在行坐标x和列坐标y的 交点上找到的元是yx,即先操作x,后操作y。每一 行和每一列都是元的重新排列。
C6轴: C6轴包括C2 和C3 的全部对称操作。
1.3 反演操作和对称中心 i
反演操作: 将分子的各点移到对称中心连线的延长线上,
且两边的距离相等。若分子能恢复原状,即反演操 作。
✔对称因素:对称中心 i ✔特点:延长线,等距
除位于对称中心的原子外,其余均成对出现
若对称中心位置在原点 (0,0,0)处,反演操作i的表 示矩阵为:
✓ 一重反轴=对称中心,二重反轴=镜面,独立的反 轴只有I4 。则具有这三种对称操作的无旋光性, 不具有这3种对称元素的分子都可能有旋光性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点线
面
对
对
对
称
称
称
中
轴
面
心.
(1)旋转轴(Cn ) 和旋转操作 =2/n
分子中若存在一条轴线,绕此轴旋转2/n的角度能 使分子复原,就称此轴为旋转轴, 符号为Cn . 旋转可以实 际进行,为真操作;相应地,旋转轴也称为真轴. n-轴次
Cˆn
H2O2中的C2
• 定义:在具有多个旋转轴的分子中,轴次最高的旋 转轴叫主轴。AX3分子的主轴是C3。
熊夫利斯记号隐含了该点群中代表性的对称元素符 号。
例如:H2O分子,有1个C2轴,2个v反映面,所以属于
C2v点群,SO2,H2S也属于此点群;
NH3分子,它有1个C3轴和3个v反映面,属于C3v
点群,类似的如CHCl3,NF3等。
3.2.2 主要点一群些化学中重要的点群
点群 对 称 元 素(未包括恒等元素)
找出Re2Cl82-离子的对称元素
Re-Re连线是一根C4轴,它同时 也是C2轴; 两根通过棱柱相对的垂直边中
Cl
Cl 心的二重轴C2,
两根通过相对的垂直面中心的
Cl
Cl
二重轴C2’’ 平分Re-Re键和全部垂直边的对
Re
称面σh
Re Cl
两个包含相对垂直边的平面
Cl
σv’σv’’ 两个切割相对垂直面中心的平
面用σd 表示
试找出分子中的镜面
重叠式C2H6
对称面的性质
• 通过对称面连续进行两次反映,分子中所 有原子均回到起始位置,得到起始构型的 恒等构型,即σ2=E。由此推得,σ2n=σ2=E, σ2n+1=σ,n为整数。
(3) 对称中心(i )与反演操作
分子中若存在一点,将每个原子通过这一点引连线并延 长到反方向等距离处而使分子复原,这一点就是对称中心i, 通过对称中心使分子复原的操作叫反演.反演操作用i 表示。
进行反映,产生一个不可分辨的构型,那么这个轴就是n重旋转 -反映轴,称作映轴,相应的对称元素称为映轴Sn 。
Sn = σ Cn 复合操作. 旋转、反映的两步操作顺序可以反过来. Sn是虚轴. 对于Sn,若n等于奇数,则Cn和与之垂直的σ都独立存在;若 n等于偶数,则有Cn/2与Sn共轴,但Cn和与之垂直的σ并不一定独 立存在.
正四面体 正六面体 正八面体 正十二面体 正二十面体
群 Td
Oh
Oh
Id
Ih
1) Td群 (正四面体构型的分子)
对称元素:3个C2,4个C3,3个S4 , 6个d
Td Eˆ,3Cˆ2,4Cˆ3,4Cˆ32,3Sˆ41,3Sˆ43,6ˆd
24阶群
C3
C2 (S4)
CH4
P4
d
CH4、P4、GeH4、SO42-、ClO4-、CrO4-、MnO4-
C4 h
SF6
立方烷
C3
d
UF6、SF6、CoF63-、Mn(OH2)62+、Fe(CN)64-、Co(CO)6
5. 线性分子 Cv 无对称中心
CO,HCN,NO,HCl,N2O
元素:C 和无穷个v
Dh 有对称中心 CO2,O2,N2,C2H2
元素:C 和无穷个v 、无穷个垂直于C 的C2, h ,i
C2H4, N2O4 D2h
C6H6 D6h
重叠式C2H6 D3h
Cl
Cl
Cl Cl
Re
Re Cl Cl
Cl
Cl
PCl5
属于什么点群?
3) Dnd群 Dn+nd d :平分相邻两个C2轴之间的夹角
H C2
H
H
H
H
H
反式乙烷
D3d
D3d : 乙烷交错型
4. 高对称群—含有二个以上高次轴Cn(n2) Td, Oh, Ih
属于什么点群?
2. 单轴群—仅含一个Cn轴或Sn轴的群
如 Cn,Cnv,Cnh,Sn群
1) Cn群 对称元素:E, Cn n 阶群
Cl C2
H
Cl
{Eˆ , Cˆ2} C2 群 H
H
H
{Eˆ , Cˆ3 , Cˆ32}
C3
群
1,3,5-三甲基苯 部分交错式
2) Cnv群
对称元素:E, Cn, nv 阶数:2n
3.恒等元素:群中必含一恒等元素E,它和群中任一元 素的乘积即为该元素本身。 例如,aE=Ea=a。
4.逆元素:群中任一元素a必有一逆元素a-1,元素a与 其逆元素a-相乘等于恒等元素 E:aa-1=a-1a=E。
以H2O分子为例,看C2v群的性质:
1.封闭性
O
O
O
C2
v
H
H
1
2
2)Oh群:(正八面体分子)
元素:3C4,4C3,6C2, 3 h, 6d,3S4,4S6,i
Oh
Eˆ ,3Cˆ41,3Cˆ43,3Cˆ2 ,4Cˆ31,4Cˆ32 ,6Cˆ2 ',3ˆ h ,6ˆ d ,
3Sˆ41,3Sˆ43,4Sˆ61,4Sˆ65 , iˆ
48阶群
E
v
v
E
v
C2 C2 E
v v E
v
v
E
EE E
C2、σv、σv′和E的逆元素就是它们本身。
一个分子所具有的对称操作(点对称操作)的完全集 合构成一个点群(Point Group)。每个点群具有一个特定 的符号,国际上通用的分子点群符号叫SchÖnflies(熊夫 利斯)记号。
SiFClBrI
H2O2, PPh3 H2O, NH3 反-N2F2 CO,HCN Cr(C2O4)33- BF3,PtCl42- H2, Cl2
Dnd Dn的对称元素、再加一套平分每一C2轴的垂直镜面 Sn 有唯一对称元素(Sn映轴) Td 正四面体分子或离子,4C3、3C2、3S4和6d
B2Cl4,交错C2H6
CH4中的映轴S4与旋转反映操作
• 注意: C4和与之垂直的σ都不独立存在
在交错构型的乙烷分子中就有一根与C3轴重合的S6轴
对于Sn,若n等于奇数,则Cn和与之垂直的σ都独立存在
重叠型二茂铁具有S5, 所 以, C5和与之垂直的σ也都 独立存在;
S1 h ; S2 i ; S3 C3 h ; S4独立,包含C2 ; S5 C5 h ; S6 C3 i
船式环已烷
N2H4
Mn(CO)5I
属于什么点群?
3) Cnh 群: 对称元素:E, Cn, h , (Sn) 阶数:2n
F
H
CC
H
F
H O
H
B
O
O
H
C2h 群
C3h 群
C2
· H i Cl
Cl
H
σh
属于什么点群?
4) Sn群
只具有一个Sn轴
n 4, S1 Cs S2 Ci S3 C3h
等价构型 Cnn、 i2、σ2=E,恒等操作
作产生的结果和两个或多个其他操作 连续作用的结果相同,通常称这一操作为其他操 作的乘积。
Example满其足结于果分关相子系当具于A有B对A,分BC子, C,单 , D独即 施对等行分对子C称先操操后作作施,,行则若称B其和C中为A某操A些作和操,B作 的乘积。
C6H6
D6h
三角双锥 PCl5
D3h
结构
分子
点群
正四面体 CH4
Td
正八面体 SF6
Oh
夹心化合物
重叠型
S4
1,3,5,7-四甲基环辛四烯
3. 二面体群(D群) —有一个Cn轴和n个垂直于Cn的C2轴
Dn,Dnh,Dnd 1) Dn群 对称元素: E,nC2Cn 阶数:2n
C2 Cn
C2
C2
C2
D2
[Co(dien)2]3+
C2
D3
[Co(en)3]3+
2) Dnh群
对称元素: E,Cn,nC2,h, (nv, Sn) 阶数:4n
• 旋转2π/n的操作以Cn表示,每次旋转2π/n,连续完 成m次的旋转,用符号Cmn表示, 旋转角为m*2π/n。
BCl3分子有1C3、3C2
Cn的性质
• n次Cn, 共生成n个操作:Cn, C2n, …,Cnn , 旋转角度依次为:2π/n, 2*2π/n,…, n*2π/n=2π。Cnn的效果为不动,得到恒等 构型。不动操作亦即恒等操作,通常以E 表示,故Cnn=E.
(5) 恒等操作E
对分子不作任何动作构成恒等操作。一切分子都 具有这个对称元素。因为对分子不作任何动作, 这个分子的状况是不会改变的。似乎这个元素是 个毫无价值的对称元素,但因群论计算中要涉及 它,所以必须包括。
恒等操作与等价操作
恒等操作是分子恒等不变,各原子的位置与最 初完全相同;
其他对称操作中,经过一次操作以后分子取向 复原,称为等价操作,但并不是跟原来完全相同。
H
H
2
1
H
H
1
2
σv′
2.结合律
vC2
v
C2
v
v v v E
C2 v v C2C2 E
则有
C2
v
v C2
v v
3.恒等元素
4.逆元素
EC2 C2 E C2
E v v E v
C2
O
H
