高二数学科组集体备课(抛物线教案)
高二数学集体备课课时教案设计抛物线第二课时

高二数学集体备课课时教案设计
一、知识与技能:1. 能根据方程求焦点和准线 2、已知条件判断抛物线标准方程的形式 3. 能根据
抛物线的定义及标准方程的形式求抛物线的标准方程3.能利用准线、焦点间的关系求标准方程并会进行分类讨论。
二、过程与方法:通过习题进一步让学生对抛物线的各种形式加强应用.
三、情感态度与价值观:激发学生学习兴趣,培养学生动手能力,分类讨论、类比的数学思想方法.
培养学生的应用意识.
(1)(2)(3)(4)
:求抛物线
学生回答:
学术训练:1:抛物线上一点M 到焦点的距离是a()则M
上与焦点距离等于。
高二数学科组集体备课抛物线教案
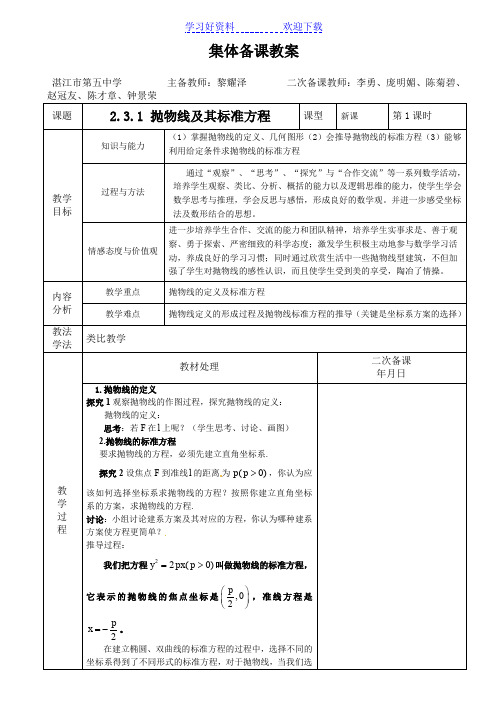
例2点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.
解:
变式训练2:
在抛物线y2=2x上求 一点P,使P到焦点F与到点A(3,2)的距离之和最小.
解:
随堂练习1P67练习1
1根据下列条件写出抛物线的标准方程:
(1)焦点是
(2)准线方程是
(3)焦点到准线的距离是2
随堂练习2P67练习2(时间有多于则完成)
情感态度与价值观
进一步培养学生合作、交流的能力和团队精神,培养学生实事求是、善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学习活动,养成良好的学习习惯;同时通过欣赏生活中一些抛物线型建筑,不但加强了学生对抛物线的感性认识,而且使学生受到美的享受,陶冶了情操。
内容
分析
教学重点
抛物线的定义及标准方程
教后
反思
在教学过程中,我发现学生对准线的概念不够熟练,并且未能真正掌握椭圆的第二定义,所以在类比学习的过程中,知识的转化不够流畅。如果需要改良教学效果,我认为:
(1)铺垫的知识在前面必须细致的讲解。
(2)引入的过程中,讲解其中的联系时务必把握好细节。
以上是我的教学反思。
集体备课教案
湛江市第五中学主备教师:黎耀泽二次备课教师:李勇、庞明媚、陈菊碧、赵冠友、陈才章、钟景荣
课题
2.3.1抛物线及其标准方程
课型
新课
第1课时
教学
目标
知识与能力
(1)掌握抛物线的定义、几何图形(2)会推导抛物线的标准方程(3)能够利用给定条件求抛物线的标准方程
过程与方法
通过“观察”、“思考”、“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,使学生学会数学思考与推理,学会反思与感悟,形成良好的数学观。并进一步感受坐标法及数形结合的思想。
高中数学抛物线教案

高中数学抛物线教案
教学目标:
1. 能够理解抛物线的定义和特点;
2. 能够求解抛物线的顶点、焦点、焦距等相关参数;
3. 能够应用抛物线知识解决实际问题。
教学重点:
1. 抛物线的标准方程;
2. 抛物线的顶点、焦点和焦距;
3. 抛物线的相关实际问题。
教学难点:
1. 利用给定的抛物线方程求解相关参数;
2. 解决实际问题时的抽象思维能力。
教学准备:
1. 投影仪、电脑或手写板;
2. 教材、讲义、课件;
3. 实例题目。
教学过程:
一、引入:
1. 引导学生回顾抛物线的定义和特点;
2. 提出学生熟悉的实际例子,如抛物线反射问题或者悬挂问题,引发学生兴趣。
二、讲解:
1. 讲解抛物线的标准方程及与二次函数的关系;
2. 讲解抛物线的顶点、焦点、焦距、对称轴等相关概念;
3. 解析求解抛物线的顶点、焦点和焦距的方法。
三、练习:
1. 给学生提供一些抛物线的相关例题,让学生自行求解;
2. 给学生布置一些实际问题,让学生应用抛物线知识解决。
四、总结:
1. 总结抛物线的相关知识点和解题方法;
2. 强调学生在学习数学知识时要注重实际应用。
五、作业:
1. 布置相关的抛物线练习题,让学生巩固知识点;
2. 提出实际问题,要求学生应用所学知识解决。
教学反思:
通过本节课的教学,学生应该能够掌握抛物线的相关知识,能够正确求解抛物线的参数和应用抛物线知识解决实际问题。
教师也应该注意引导学生运用数学知识解决实际问题,提高学生的抽象思维能力和解决问题的能力。
人教版高中数学抛物线教案

人教版高中数学抛物线教案
主题:抛物线
教材版本:人教版高中数学
教学内容:抛物线的基本概念和性质
教学目标:
1. 了解抛物线的定义和基本特征;
2. 熟练掌握抛物线的标准方程;
3. 能够解决与抛物线相关的问题。
教学重点和难点:
重点:抛物线的标准方程和性质。
难点:能够灵活运用抛物线的性质解决问题。
教学过程:
一、导入(5分钟)
教师介绍抛物线的概念,引出本课要学习的内容。
二、讲解(15分钟)
1. 抛物线的定义和形状;
2. 抛物线的标准方程;
3. 抛物线的焦点、准线和顶点。
三、练习(20分钟)
1. 让学生在纸上绘制抛物线,并编写标准方程;
2. 给学生一些练习题,让他们独立解决问题。
四、总结(5分钟)
教师总结本节课的要点,强调抛物线的重要性和应用。
五、作业布置(5分钟)
布置相关练习题作业,鼓励学生在家里复习和巩固所学知识。
※教学结束※
教学反思:
本节课通过讲解抛物线的定义、性质和标准方程,帮助学生更好地理解抛物线的基本概念。
但是在练习环节,部分学生遇到了困难,需要更多的实践和巩固。
下次课程将设计更多的
练习题,加深学生对抛物线的理解和掌握。
2024年抛物线教学设计抛物线教案

2024年抛物线教学设计抛物线教案一、教学内容本节课选自人教版高中数学选修22第二章“抛物线及其标准方程”,具体内容包括:抛物线的定义、标准方程、简单几何性质以及抛物线在实际问题中的应用。
二、教学目标1. 理解并掌握抛物线的定义,能够熟练推导出抛物线的标准方程。
2. 熟悉抛物线的简单几何性质,能够运用这些性质解决实际问题。
3. 培养学生的空间想象能力和逻辑思维能力,激发学生对数学学习的兴趣。
三、教学难点与重点教学难点:抛物线标准方程的推导以及抛物线几何性质的理解。
教学重点:抛物线的定义、标准方程及其简单几何性质。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:直尺、圆规、练习本。
五、教学过程1. 实践情景引入利用多媒体课件展示生活中的抛物线实例,如抛物线形拱桥、抛物线运动轨迹等,引导学生观察并思考抛物线的特点。
2. 知识讲解(1)抛物线的定义:以一个定点(焦点)为顶点,到该点的距离等于到一条定直线(准线)的距离的所有点的集合。
(2)抛物线的标准方程:y^2=4ax(开口向右),y^2=4ax(开口向左)。
(3)抛物线的简单几何性质:对称性、顶点、焦点、准线等。
3. 例题讲解(1)求抛物线y^2=8x的焦点和准线。
(2)已知抛物线的焦点为(3,0),求抛物线的标准方程。
4. 随堂练习(1)求抛物线y^2=12x的顶点、焦点和准线。
(2)已知抛物线的顶点为(0,4),求抛物线的标准方程。
5. 小结与巩固六、板书设计1. 抛物线的定义2. 抛物线的标准方程y^2=4ax(开口向右)y^2=4ax(开口向左)3. 抛物线的简单几何性质4. 例题及解答七、作业设计1. 作业题目(1)求抛物线x^2=16y的焦点、顶点和准线。
(2)已知抛物线的焦点为(0,3),求抛物线的标准方程。
2. 答案八、课后反思及拓展延伸1. 探讨抛物线在实际问题中的应用,如建筑设计、运动轨迹等。
2. 引导学生研究抛物线与其他圆锥曲线(如椭圆、双曲线)之间的联系与区别。
高二数学《抛物线中的焦点弦问题》集体备课

高二数学《抛物线中的焦点弦问题》集体备课1. 引言本次集体备课的主题是《抛物线中的焦点弦问题》。
通过这个问题的讨论与研究,旨在帮助学生理解抛物线的性质,并且进一步加深对焦点与弦的概念的认识。
本次备课内容包括基本概念的介绍、问题的分析与解决思路以及相关练习题目的设计。
2. 抛物线的基本概念抛物线是数学中的一种二次曲线。
它的定义是所有到一个定点F(焦点)的距离与到一个定直线(准线)的距离之比都相等的点的轨迹。
抛物线还有一条对称轴,过焦点与对称轴垂直的直线称为准线。
3. 焦点与弦的概念3.1 焦点焦点是抛物线的一个重要概念,也是定义抛物线的关键。
焦点的定义是指到焦点的距离与到准线的距离之比恒定。
焦点在抛物线的对称轴上。
3.2 弦弦是抛物线上两点之间的线段。
具体而言,我们可以通过两个焦点之间的任意两点来确定一条抛物线上的弦。
4. 问题分析与解决思路4.1 问题分析我们希望通过集体备课的方式解决以下问题:•如何确定一条抛物线上的焦点?•如何确定一条抛物线上的弦?•如何利用焦点与弦进行问题求解?4.2 解决思路•通过焦点的定义和抛物线的特性,学生可以通过已知焦点的坐标和抛物线的准线来确定抛物线的方程。
•对于已知抛物线方程的问题,学生可以通过代入已知的点坐标,求解未知参数,从而确定焦点的坐标。
•如果已知抛物线上的两个点,学生可以通过求解这两点确定的弦的过程来解决相关问题。
5. 练习题目设计5.1 题目一已知抛物线的焦点为F(-1, 2),准线方程为y = 1。
求出该抛物线的方程,并画出图像。
5.2 题目二已知抛物线的方程为y = ax^2 + bx + c,并且经过点P(1, 4)和Q(-2, -1)。
求出a、b、c的值,并确定抛物线的焦点。
5.3 题目三已知抛物线上的两点P(2, 7)和Q(3, 10),求出过点P和Q的弦的方程,并求出该弦与准线的交点坐标。
6. 总结通过本次的集体备课,我们对于《抛物线中的焦点弦问题》有了更深入的理解。
高中抛物线数学教案

高中抛物线数学教案
主题:抛物线
一、教学目标:
1. 理解抛物线的定义和性质;
2. 掌握抛物线的标准方程及相关计算方法;
3. 熟练运用抛物线相关知识解决实际问题。
二、教学重点和难点:
重点:抛物线的定义、标准方程及相关性质;
难点:抛物线的几何意义及应用问题的解决。
三、教学过程:
1. 导入新知识(5分钟)
通过展示抛物线的图片和实际应用场景,引导学生了解抛物线的形态和特点。
2. 学习抛物线的定义和性质(15分钟)
讲解抛物线的定义,并介绍抛物线的焦点、顶点、对称轴等性质,让学生理解抛物线的基本概念。
3. 学习抛物线的标准方程(20分钟)
教师讲解抛物线的标准方程及其推导过程,让学生掌握如何根据给定的抛物线特点确定其标准方程。
4. 练习抛物线相关计算(20分钟)
让学生通过练习题目,熟悉抛物线的计算方法,包括焦点、顶点、焦距等的计算。
5. 解决实际问题(15分钟)
通过实际应用问题的讨论与解答,引导学生灵活运用抛物线知识解决实际问题,并培养学生的数学建模能力。
6. 总结和作业布置(5分钟)
对抛物线相关知识进行总结,并布置相关练习作业,巩固学生的学习成果。
四、教学手段:
1. 教师讲解;
2. 课堂练习;
3. 实际应用问题讨论。
五、教学反思:
本节课主要围绕抛物线的定义、标准方程及相关计算展开,注重培养学生的问题解决能力和建模能力。
通过实践与讨论,让学生真正理解抛物线的几何意义和应用价值,为他们的数学学习打下坚实基础。
高二数学教案:抛物线教案人教版

人教版抛物线教案
一.教学目的:
1.掌握抛物线的概念.
2.掌握抛物线的标准方程及其应用. 3.理解并应用抛物线的几何性质. 二.重点难点:
1.重点:抛物线的标准方程及其应用.抛物线的几何性质. 2.难点:抛物线的几何性质. 三.教学过程:
引入新课:与一定点的距离和一条定直线的距离比是常数e的点的轨迹,当e<1时,是椭圆,当e>1时,是双曲线。
当e=1时,是什么曲线呢?(让同学们看课件抛物线的定义部分,然后让学生回答,给出抛物线的定义。
)
如图平面内与一个定点F 和一条定直线L 的距离相等的点的
轨迹叫做抛物线.
结合课件,让学生推导抛物线的标准方程. 取过焦点F且垂直与准线L的直线为x轴,x轴与L相交于点K,以线段KF 的垂直平分线为y轴,如右图.设KF =p,
则焦点F的坐标为F(2p ,0),准线L 的方程为:x=-2
p
.
设抛物线上的点M(x,y)到L的距离为d.抛物线也就是集合P={MMF =d}.
∵MF =2
2y p x +⎪⎭
⎫ ⎝⎛-
, d=2p x +,
∴2
2y p x +⎪
⎭
⎫ ⎝⎛
-
=2p x + 将上式整理可得抛物线的标准方程:y2
=2px(p>0)
最后让学生看课件抛物线的标准方程部分,加深印象.
接着让学生看e与图线形状之间的关系.让学生对抛物线、椭圆、双曲线有一个整体认识,为后面综合应用打好基础.
例题1:求下列抛物线的焦点坐标和准线方程:
⑴x2=2y:
⑵y2-6x=0:
例题2:拱形桥洞是一段抛物线,宽7m,高为0.7m,求这条抛物线的方程.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集体备课教案
湛江市第五中学主备教师:黎耀泽二次备课教师:李勇、庞明媚、陈菊碧、赵冠友、陈才章、钟景荣
课题 2.3.1 抛物线及其标准方程课型新课第1课时
教学目标
知识与能力
(1)掌握抛物线的定义、几何图形(2)会推导抛物线的标准方程(3)能够
利用给定条件求抛物线的标准方程
过程与方法
通过“观察”、“思考”、“探究”与“合作交流”等一系列数学活动,培养学生观察、类比、分析、概括的能力以及逻辑思维的能力,使学生学会
数学思考与推理,学会反思与感悟,形成良好的数学观。
并进一步感受坐标
法及数形结合的思想。
情感态度与价值观
进一步培养学生合作、交流的能力和团队精神,培养学生实事求是、善于观察、勇于探索、严密细致的科学态度;激发学生积极主动地参与数学学
习活动,养成良好的学习习惯;同时通过欣赏生活中一些抛物线型建筑,不
但加强了学生对抛物线的感性认识,而且使学生受到美的享受,陶冶了情操。
内容分析教学重点抛物线的定义及标准方程
教学难点抛物线定义的形成过程及抛物线标准方程的推导(关键是坐标系方案的选择)
教法
学法
类比教学
教学过程
教材处理
二次备课
年月日 1.抛物线的定义
探究1观察抛物线的作图过程,探究抛物线的定义:
抛物线的定义:
思考:若F在l上呢?(学生思考、讨论、画图)
2.抛物线的标准方程
要求抛物线的方程,必须先建立直角坐标系.
探究2 设焦点F到准线l的距离为(0)
p p>,你认为应
该如何选择坐标系求抛物线的方程?按照你建立直角坐标
系的方案,求抛物线的方程.
讨论:小组讨论建系方案及其对应的方程,你认为哪种建系
方案使方程更简单?
推导过程:
我们把方程22(0)
y px p
=>叫做抛物线的标准方程,
它表示的抛物线的焦点坐标是,0
2
p
⎛⎫
⎪
⎝⎭
,准线方程是
2
p
x=-。
在建立椭圆、双曲线的标准方程的过程中,选择不同的
坐标系得到了不同形式的标准方程,对于抛物线,当我们选择如图三种建立坐标系的方法,我们也可以得到不同形式的抛物线的标准方程:
(学生分前两排,中间两排,后面两排三组分别计算三种情况,一起填充表格)
图形
标准方程
焦点坐标
准线方程
(三)例题
例1(1)已知抛物线的标准方程是2
6y x =,求它的焦点坐标和准线方程,
(2)已知抛物线的焦点是()0,2F -,求它的标准方程.
解: 变式训练1:
(1) 已知抛物线的准线方程是x =—
4
1
,求它的标准方程.
(2) 已知抛物线的标准方程是2y 2+5x =0,求它的焦点坐
标和准线方程. 解:
例2 点M 与点F (4,0)的距离比它到直线l :x +5=0的距离小1,求点M 的轨迹方程.
解: 变式训练2:
在抛物线y 2=2x 上求一点P ,使P 到焦点F 与到点A (3,2)的距离之和最小.
解: 随堂练习1
P 67练习1
1 根据下列条件写出抛物线的标准方程: (1)焦点是()30F , (2)准线方程是1
4
x =-
(3)焦点到准线的距离是2 随堂练习2P 67练习2 (时间有多于则完成)
(四)小结
1、抛物线的定义;
2、抛物线的四种标准方程;
3、注意抛物线的标准方程中的字母P 的几何意义. (五)作业布置 (1)必做题 P 73 A 组1,2,3 (2)选做题 P 74 B 组1
测练题目1.抛物线y2=ax(a≠0)的准线方程是( )
(A)
4
a
x=-;(B)x=
4
a
;(C)
||
4
a
x=-;(D)x=
||
4
a
2.抛物线2
1
x
m
y=(m≠0)的焦点坐标是()
(A) (0,
4
m
)或(0,
4
m
-);(B) (0,
4
m
)
(C) (0,
m
4
1
)或(0,
m
4
1
-);(D) (0,
m
4
1
)
3.根据下列条件写出抛物线的标准方程:(1)焦点是F(0,3),(2)焦点到准线的距离是2.
4.求下列抛物线的焦点坐标和准线方程:(1)y2=20x;(2)x2+8y=0.
5.点M到点(0,8)的距离比它到直线y=-7的距离大1,求M点的轨迹方程.。
