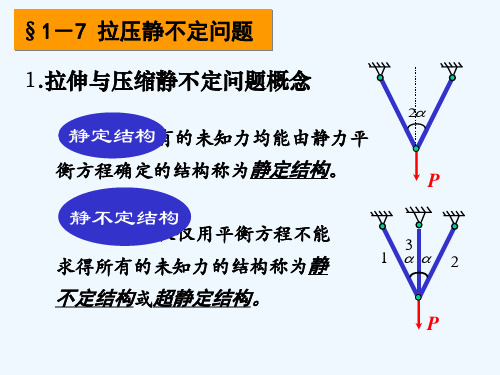
拉压静不定问题(精)
合集下载
材料力学-拉、压

6
单位:Pa=N/m2,1Mpa=106Pa,1GPa=109Pa
3、正应力、剪应力
正应力 :垂直与截面的应力,指向外法线方向为正。 剪应力 :相切于截面的应力,左上右下为正。 4、拉、压杆横截面上的应力 对于等截面直杆,横截面上的 应力分布均匀,因此有 垂直截面:
0
角的斜截面:
7
5、圣维南原理 如果杆端的外加载荷在静力 学上等效,则端部以外区域的应 力差异甚微。所以不考虑端部加 载方式的影响。
4
2、截面法 因内力是物体内部各部分之间的相互作用力,所以截断 内部的联系,可揭示、研究内力。 这种假想地用一个截面将构件截开,从而揭示内力,并 确定内力的方法,称为截面法。 其步骤:参考:教材112页 (1)截开两部分 内力的方向: 材料力学中从变形的角度规定:拉为正、压为负 与静力学中的力的正、负规定不同。
11
二、正应力、应力--应变关系 从胡克定律可知,杆件的弹性模量 E、横截面面积 A、轴力 N 相同时,杆件的长度 l 越大,变形量 l 越大。因此单单绝对 变形量 l 还不能反映杆件的变形程度。所以引入相对变形量 的概念---正应变 。 则有
l , 单位长度的变形量,无量纲,伸长为正。 l
1 2 A A A 1 2
(1) (2) (3)
24
未知数4个,方程仅三个,必须补充一个方程:
2l1 l2 S1l1 而 l1 E1 A1
- - - - - - - 变形协调条件 S 2l2 , l2 , 且 l1 l2 E2 A2 (4)
S1 S2 2 - - - - - - - -变形协调方程 E1 A1 E2 A2 2P S1 E2 A2 1 4 E1 A1 4P S2 E1 A1 4 E2 A2 2 4 S1 P , S 2 P 5 5
单位:Pa=N/m2,1Mpa=106Pa,1GPa=109Pa
3、正应力、剪应力
正应力 :垂直与截面的应力,指向外法线方向为正。 剪应力 :相切于截面的应力,左上右下为正。 4、拉、压杆横截面上的应力 对于等截面直杆,横截面上的 应力分布均匀,因此有 垂直截面:
0
角的斜截面:
7
5、圣维南原理 如果杆端的外加载荷在静力 学上等效,则端部以外区域的应 力差异甚微。所以不考虑端部加 载方式的影响。
4
2、截面法 因内力是物体内部各部分之间的相互作用力,所以截断 内部的联系,可揭示、研究内力。 这种假想地用一个截面将构件截开,从而揭示内力,并 确定内力的方法,称为截面法。 其步骤:参考:教材112页 (1)截开两部分 内力的方向: 材料力学中从变形的角度规定:拉为正、压为负 与静力学中的力的正、负规定不同。
11
二、正应力、应力--应变关系 从胡克定律可知,杆件的弹性模量 E、横截面面积 A、轴力 N 相同时,杆件的长度 l 越大,变形量 l 越大。因此单单绝对 变形量 l 还不能反映杆件的变形程度。所以引入相对变形量 的概念---正应变 。 则有
l , 单位长度的变形量,无量纲,伸长为正。 l
1 2 A A A 1 2
(1) (2) (3)
24
未知数4个,方程仅三个,必须补充一个方程:
2l1 l2 S1l1 而 l1 E1 A1
- - - - - - - 变形协调条件 S 2l2 , l2 , 且 l1 l2 E2 A2 (4)
S1 S2 2 - - - - - - - -变形协调方程 E1 A1 E2 A2 2P S1 E2 A2 1 4 E1 A1 4P S2 E1 A1 4 E2 A2 2 4 S1 P , S 2 P 5 5
第二章-轴向拉伸与压缩-拉压静不定

三、拉压静不定问题举例
1.不同材料组成的组合杆件 不同材料组成的组合杆件 变形特点:两种材料的伸长或缩短变形相同。 变形特点:两种材料的伸长或缩短变形相同。 弹性模量为E 横截面面积为A 弹性模量为 1、横截面面积为 1的实心 圆杆与弹性模量为E 横截面面积为A 圆杆与弹性模量为 2 、 横截面面积为 2 的 圆筒用刚性板联接,如图a)所示 试求在F 所示。 圆筒用刚性板联接,如图 所示。试求在 力作用下圆杆和圆筒的应力。 力作用下圆杆和圆筒的应力。 解:受力分析如图,可知为一次静不定问题。 受力分析如图,可知为一次静不定问题。 (1)平衡条件(平衡方程) 平衡条件(平衡方程) 平衡条件
a
受力分析如图示,可知为一次静不定。 解:受力分析如图示,可知为一次静不定。
(1)平衡方程
a
N1 a
∑F = 0
y
N1 − N2 = 0
(2)变形几何方程 (2)变形几何方程
∆L = ∆LT + ∆LN = 0
N2 a
(3)本构方程 )
N1a N2a ∆L = 2a∆Tα ; ∆LN = −( + ) T EA EA 1 2
∆L A 3 1
(2)变形几何方程 (2)变形几何方程
∆L 1
α α
A
δ
∆L 2
∆L 1 ∆L3 + =δ cosα
E A cos2 α 1 1 FN1 = FN2 = ⋅ L3 1+ 2cos3 α E A / E3 A 1 1 3
(4)联立求解 联立求解
(3)本构方程 本构方程
δ
FN3L3 FN1L 1 + =δ 2 E3 A E A cos a 3 1 1
∆L2
静不定问题1

第2章 拉伸与压缩杆件的应力变形分析与强度计算 章
结论与讨论
多余约束使结构由静定变为静不定,问题由静力平衡可 多余约束使结构由静定变为静不定 , 解变为静力平衡不可解,这只是问题的一方面。 解变为静力平衡不可解, 这只是问题的一方面。 问题的另一 方面是,多余约束对结构或构件的变形起着一定的限制作用, 方面是,多余约束对结构或构件的变形起着一定的限制作用 , 而结构或构件的变形又是与受力密切相关的, 而结构或构件的变形又是与受力密切相关的,这就为求解静 不定问题提供了补充条件。 不定问题提供了补充条件。
第2章 拉伸与压缩杆件的应力变形分析与强度计算 章
结论与讨论
未知力个数与独立的平衡方程数之差,称为静不定次数 未知力个数与独立的平衡方程数之差 , 称为 静不定次数 (degree of statically indeterminate problem)。在静定结构上附 。 加的约束称为多余约束 多余约束(redundant constraint),这种“多余” 加的约束称为多余约束 ,这种“多余” 只是对保证结构的平衡与几何不变性而言的, 只是对保证结构的平衡与几何不变性而言的,对于提高结构 的强度、刚度则是需要的。 的强度、刚度则是需要的。 关于静定与静不定问题的概念,本书将在第 章中介绍。 章中介绍。 关于静定与静不定问题的概念,本书将在第3章中介绍 但是,由于那时所涉及的是刚体模型, 但是, 由于那时所涉及的是刚体模型 ,所以无法求解静不定 问题。现在,研究了拉伸和压缩杆件的受力与变形后, 问题。 现在, 研究了拉伸和压缩杆件的受力与变形后 ,通过 变形体模型,就可以求解静不定问题。 变形体模型,就可以求解静不定问题。
第2章 拉伸与压缩杆件的应力变形分析与强度计算 章
结论与讨论
3-1 静不定(14年) (拉压应力作业问题)

5
(压应力)
拉压杆超静定问题
例 阶梯钢杆上下两段在T1=5℃被固定,上下
两段面积为=cm2 , =cm2,当温度 升至T2 = 25℃时,求各杆的温度应力。已知, a
FN1
a
弹性模量E=200GPa,线膨胀系数为
解:① 平衡方程
a
② 变形方程
a FN2
拉压杆超静定问题
③ 本构方程
l l1 l 2 l 3 l4 0
FN i li l i EA
FN 3 FN A P FN 4 FN A P 2P 3P
例2、平行力系: 求各杆内力。 已知:AB为刚性梁,两杆A=1000mm2,P=50kN •几何:Δl2=2Δl1
l a A
P
A
FN1
静不定结构的特点(2) ———装配应力
B D B C D
静定结构 ——无装配应力
A
A
静不定结构 ! ——?
已知:三杆EA相同,1杆制造误差δ,求装配内力
B○ 2 ⊿l1 ⊿l2 α
○
C α 3
○
D
解题思路:因制造误差,
装配时各杆必须变形,
1
因此产生装配内力。
l
δ
几何方程: ⊿l1+⊿l2 / cosα = δ 物理方程 ?虎克定律!
实质:未知力的数目等于静力平衡方程的数目。
2)静不定问题——仅用静力平衡方程不能求 出全部未知力。又称超静定问题。 实质:未知力的数目多于静力平衡方程的数目。
二. 静不定问题的解法: 1. 判断静不定次数: 方法1: 未知力数目-平衡方程数目 方法2:多余未知力数目 2. 列平衡方程 3. 列几何方程:反映各杆变形之间的 关系,需要具体问题具体分析。 4. 列物理方程:变形与力的关系。 5. 列补充方程:物理方程代入几何方 程即得。
(压应力)
拉压杆超静定问题
例 阶梯钢杆上下两段在T1=5℃被固定,上下
两段面积为=cm2 , =cm2,当温度 升至T2 = 25℃时,求各杆的温度应力。已知, a
FN1
a
弹性模量E=200GPa,线膨胀系数为
解:① 平衡方程
a
② 变形方程
a FN2
拉压杆超静定问题
③ 本构方程
l l1 l 2 l 3 l4 0
FN i li l i EA
FN 3 FN A P FN 4 FN A P 2P 3P
例2、平行力系: 求各杆内力。 已知:AB为刚性梁,两杆A=1000mm2,P=50kN •几何:Δl2=2Δl1
l a A
P
A
FN1
静不定结构的特点(2) ———装配应力
B D B C D
静定结构 ——无装配应力
A
A
静不定结构 ! ——?
已知:三杆EA相同,1杆制造误差δ,求装配内力
B○ 2 ⊿l1 ⊿l2 α
○
C α 3
○
D
解题思路:因制造误差,
装配时各杆必须变形,
1
因此产生装配内力。
l
δ
几何方程: ⊿l1+⊿l2 / cosα = δ 物理方程 ?虎克定律!
实质:未知力的数目等于静力平衡方程的数目。
2)静不定问题——仅用静力平衡方程不能求 出全部未知力。又称超静定问题。 实质:未知力的数目多于静力平衡方程的数目。
二. 静不定问题的解法: 1. 判断静不定次数: 方法1: 未知力数目-平衡方程数目 方法2:多余未知力数目 2. 列平衡方程 3. 列几何方程:反映各杆变形之间的 关系,需要具体问题具体分析。 4. 列物理方程:变形与力的关系。 5. 列补充方程:物理方程代入几何方 程即得。
材料力学拉压静不定问题
§1-8 温度应力和装配应力
一、温度应力
在超静定结构中,由于各个杆件的变形受到相互的 制约,当温度改变时,必然要在杆内引起附加应力,由 于温度改变而在杆内引起的应力称为温度应力。
对于无约束的杆件,当温度变化为 t t2t1时,杆 件的变形为:
lt tl
式中: ——为材料的线膨胀系数。
例 图示结构,杆①、杆② EA均相同,当杆①温
P
0.72P
求结构的许可载荷
N 1 0 .0P 7 A 1 1
角钢面积由型钢表查得: A1=3.086 cm2
P 1 A 1 1 / 0 . 0 7 3 0 8 . 6 1 6 0 / 0 . 0 7 7 0 5 . 4 k N
N 2 0 .7P 2 A 2 2
P 2 A 2 2 / 0 . 7 2 2 5 0 2 1 2 / 0 . 7 2 1 0 4 2 k N
变形内力关系(物理方程)
方程
P
N3
N1
N2
A
P
例2 求图示两端固定等直杆的约束反力
解:解除约束,以已知方向约束反力代替
EA
EA
平衡方程: PRARB0
A
a
P B 为得到变形协调方程,解除多余约束,分别
b
考虑外力和多余约束反力产生的位移叠加
设B为多余约束,此处的实际位移必须为0
RA
P
R B 几何方程: lP lRB
PP
PP
解:平衡方程:
yy
Y 4 N 1 N 2 P 0
44NN1 1
N2
几何方程
N2
L1 L2
物理方程及补充方程:
L1N E11A L1 1 N E22A L2 2 L2
04-2.7 拉压静不定问题

A l1
F
研究变形
内力假设受拉
变形假设伸长
内力假设与变形假设一致 !
注意事项2:几何方程的求法
B
CD
1
2 3
l3 A l2
A 方法1
l1 F
B
CD
1
2 3
l2Al3
A l1
F
方法2
新节点向原杆作垂线 原节点向新位置作垂线
Statically indeterminate problem 特点:未知力的数目多于静力平衡方程的数目
未知力的数目 pk. 静力平衡方程的数目
例子
B
C
1 2
A
F
y
FN1
FN2
A
x
F
未知力数目: 2 ( FN1 , FN2 ) 静力平衡方程数目: 2 ( ∑Fx = 0, ∑Fy = 0 ) 判断: 静定结构——静定问题
仅用静立平衡方程 便能求解全部未知量
例子
FN2 FN3
FN1
FN4
F
F
未知力数目:4个 静力平衡方程数目:2个 判断:静不定结构,静不定问题
需要补充 2 个方程
3. 静不定次数
Degree of statical indeterminancy
未知力数目与平衡方程数目之差
也是需要补充的方程数目
FN2 FN3
5.25°
2°
5°
4° 2.75°
5.25° 2.75°
4°X5=20° 4° 5° 4°X3=12°
6° 5°
Ⅲ 5°
4°X4=16° 4°
Ⅰ
纵向对接桁 Ⅳ
16
内力按刚度比分配实例2
初始设计
第十章 简单静不定问题

3、物理关系
l1
FN1l
EA cos
l3
FN 3l EA
补充方程 FN1l FN3l cos EAcos EA
FN1 FN3 cos2
FN1
FN 2
F cos2 1 2 cos3
FN 3
1
F
2 cos3
目录
例题10-2 木制短柱的4个角用4个40mm×40mm×4mm的等边角钢加固,
由平衡方程解得, F1= F2= F3=
由对称知, F4= 根F2据卡氏第二定理,
2 2 F6
F5 =F6
A
F2
F1 F6
F2’B
FN6 1 F6
FN1 2 F6 2
F5
F3
6
FNili
FNi
4
2 2
F6l
2 2 F6
2l 2F6l (1
2)
i1 EA F6
EA 2
EA EA
F6
EA
2l (1
L 1 1000 ,将杆装在两刚性支座之间,试求装配应力。
解: L FNl
EA
FN
EA L
FN E
AL
200MPa
目录
例10-4 图示杆系结构中,6杆比名义长度短δ,设各杆的抗拉刚度 都是EA,试求装配完成后,各杆的内力。
F6 F6’
解:设6杆受拉,拉力为F6。
取节点A 、B为研究对象,
静不定结构:结构的强度和刚度均得到提高
目录
二. 基本静定系(静定基),相当系统 基本静定系:解除静不定结构的多余约束后得到的静定结构。 相当系统:在静定基上加上外载荷以及多余约束力的系统。
MC
MA
材料力学2-2拉压静不定

1
ቤተ መጻሕፍቲ ባይዱ
7)组合体伸长: 6)应力: (压) (拉)
作业: P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数:k
max 0
习 题 课
例题1:图示构架,两杆的材料相同,其横截面面积之 比为A1:A2=2:3,承受载荷为P,试求: 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN,A1=100mm2,则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业:
P82 2.51
P84 2.53
soc
1
L
1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N,0 Y )1(
2
已知三杆的EA相同,3杆制造短了长度, 若将三杆用铰A装配,试求装配后各杆的受力。
解: 1)平衡方程
2)装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图:
3)物理关系:
5)联立求解:
4)补充方程:
3. 静不定问题特征: 1)各杆的受力与刚度有关; 2)静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1: D1=45mm,t = 3mm,d2=30mm,E1=210GPa, 1=1210 -61/oC, E2=110GPa, 2=16 10 - 61/oC, t从30o升高至180o(30o为装配时温度),求钢管和铜 杆内的应力以及组合体的伸长。 解:1)
ቤተ መጻሕፍቲ ባይዱ
7)组合体伸长: 6)应力: (压) (拉)
作业: P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数:k
max 0
习 题 课
例题1:图示构架,两杆的材料相同,其横截面面积之 比为A1:A2=2:3,承受载荷为P,试求: 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN,A1=100mm2,则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业:
P82 2.51
P84 2.53
soc
1
L
1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N,0 Y )1(
2
已知三杆的EA相同,3杆制造短了长度, 若将三杆用铰A装配,试求装配后各杆的受力。
解: 1)平衡方程
2)装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图:
3)物理关系:
5)联立求解:
4)补充方程:
3. 静不定问题特征: 1)各杆的受力与刚度有关; 2)静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1: D1=45mm,t = 3mm,d2=30mm,E1=210GPa, 1=1210 -61/oC, E2=110GPa, 2=16 10 - 61/oC, t从30o升高至180o(30o为装配时温度),求钢管和铜 杆内的应力以及组合体的伸长。 解:1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N AD
N N AB AC
A
A
A3
A A2
A1
P
P
B
D
C
(三)补充方程
由上面分析过程知,各杆变形量为:
AB杆变形量:l AB AA ;AD杆变形量: 1
A A3 A1
A2
l AD AA2;AC杆变形量:l形几何(协调/相容)关系:
P
图(a)
问题可解: N AB N AC
P 2 cos
二、问题的提出 在此结构竖直方向加上材料和截面
尺寸与其他两杆相同的等直杆AD后(这是工程中常见 的三杆桁架结构),求此时各杆内力 。
B D C
A
P
N AD
解: 静不定问题:仅用静力平衡 (一)静力学关系 方程求解不出结构所有未知 以节点 A为研究对象,其受力情况如 力的问题。也称为超静定问 题。相应的结构称为静不定 图( b)所示,则列平衡方程有 结构或超静定结构。
x AC AB y AC AD AB
N AB
A
N AC
(1) F 0, N sin N sin 0 0, N cos N N cos P 0 (2) F 简单静不定问题的解法:从
P
图(b)
变形几何方面寻求补充方程 两个独立方程含有三个未知量,仅凭静 力平衡方程不能求出该问题的全部解。 与平衡方程联立求解。
变形图
补充方程
例:求图示杆的支反力。
R A RB P 解:静力平衡条件:
(1)
变形协调条件: l l AC l BC 0
R A l1 RB l2 0 引用胡克定律: EA EA
由此得:
R A l1 RB l2
(2)
联立求解(1)和(2), 得:
l2 l1 RA P , RB P l l
拉压静不定问题
一、引例
B D C
图示结构,若各杆件为等直杆且材料 和截面尺寸均相同,抗拉压刚度为 EA, 杆长均为 l , 求各杆的内力。 对于该问题,取节点A作为研究对 象,受力如图(a)所示,列平衡关系 式有:
A
N N AB AC
A
P
F F
x y
0, N AC sin N AB sin 0 0, N AC cos N AB cos P 0
N AB N AC P cos2 3 1 2 cos
N AD
P 1 2 cos3
至此问题得以解决,相应地可以进行应力、应 变、强度计算(包括强度校核、截面尺寸设计、许 用外载确定)等后继计算工作。
三、求解简单静不定问题的基本步骤为:
受力图
变 形 相 容 方 程 物理 方程 平衡方程 联 立 求 解
AA 即lAB lAC 1 AA 3
B D C
在小变形下, AB杆和AC杆 变形后,其铰接点按“以切 代弧法”确定为过A1、A3作 AA1和AA3垂线的相交点A2。 又因各构件变形后仍铰接于 一点,即各构件的变形要相 容、协调,故A2点也是AD杆 变形后的铰接位置。再按 “以切代弧法”知AD杆的变 形量为AA2。
解: 变形协调条件:
lT l N
Rl 即: l T EA
R E T ( 压) A
应用一:装配应力问题
求图示2杆与1、3杆装配后引起的应力。
解:静力平衡条件:
N1 N 3 2 N 1 cos N 2
变形协调条件:
l1 l 2 h cos
引用胡克定律:
N 2 l cos N 1l h EA EA cos
应用二:温度应力问题
温度升高T
已知:构件的线膨胀系数 α ——单位长度的杆温度升高1℃时杆的伸长量。 求:由于温度改变后引起该构件横截面上的正应力。
各杆变形量如何确定?
按照变形与受力相一致的原则对各杆变形作定 性和定量分析: (1)定性方面:各杆在内力作用下沿轴向伸长 或缩短。 (2)定量方面:各杆在内力作用下沿轴向的伸 缩量须满足本构关系(或物理关系)。 (二)本例中杆件的变形量应满足的物理关系:
Nl l EA
(3)
由式(1)和式(3)知AB杆和AC杆的变形量相等, 即:
l AB l AC l AD cos
将物理关系式(3)代入(4)得
(4)
N ABl AB N AC l AC N ADl AD cos EA EA EA
化简后得补充方程:
N AB N AC N AD cos2
(5)
最后,联立式 (1)、 (2) 、(5)求解得:
